Привет, Хабр! Есть мнение, что прогнозирование временных рядов - сложная задача. Но не будем расстраиваться, ведь есть и плюсы - существует ещё большое количество задач, когда рядов сразу несколько, и такие задачи ещё сложнее! Когда начинаем сравнивать, понимаем, что прогнозировать одномерные временные ряды не так уж и сложно. А вот что делать с ситуацией, когда временной ряд обрастает параллельно идущими с ним последовательностями других параметров (многомерный ряд), какие методы и алгоритмы использовать, и что делать, если задача прогнозировать такие ряды есть, а опыта не очень много (спойлер - используйте AutoML, а пока он работает восполните пробел прочитав пару статей по теме), разбираем под катом.

Что такое временной ряд 

Если начинать совсем издалека, то это последовательность значений, упорядоченная по времени. Во временных рядах есть закономерность: текущие значения ряда связаны с предыдущими. Если такого свойства у ряда нет, то поздравляем (или не поздравляем), вы имеете дело с процессом, который прогнозировать классическими (и не очень) моделями не выйдет, в таком случае стоит смотреть в сторону Марковских процессов.

Простенькая картинка ниже иллюстрирует описанное выше свойство, - этого бэкграунда для продолжения чтения поста достаточно (Рисунок 1).

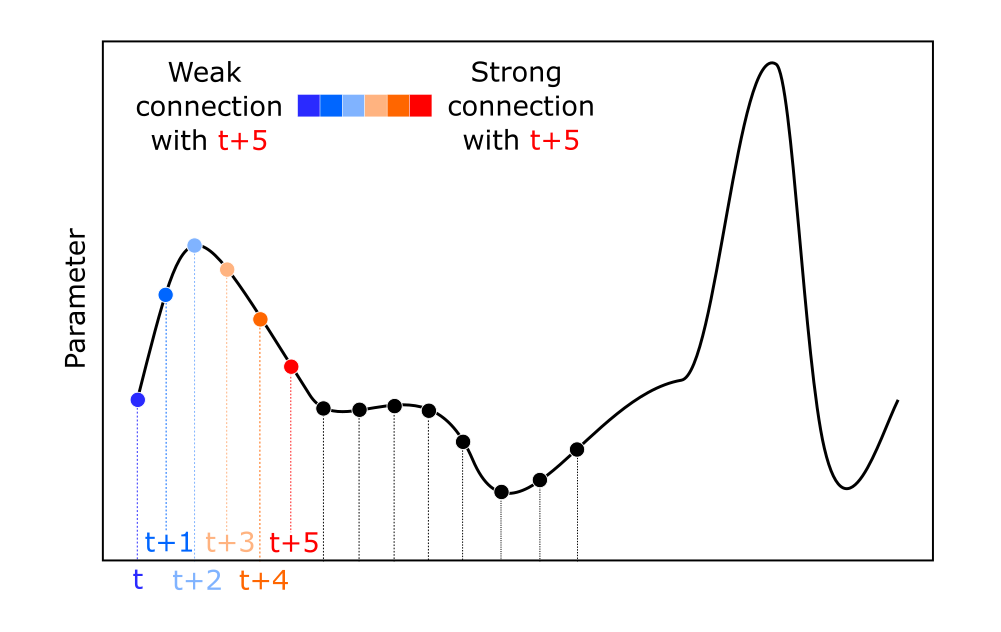
Если хочется узнать подробнее как временные ряды прогнозировать (особенно при помощи AutoML), можете изучить пост Прогнозирование временных рядов с помощью AutoML. 

Что такое многомерный временной ряд

Уже ближе к основной теме. Многомерный временной ряд - это система из нескольких одномерных рядов, где значения одного (целевого) зависят не только от предыдущих значений этого ряда, но и от значений дополнительного, или нескольких дополнительных. 

Пример того как может выглядеть многомерный временной ряд показан на Рисунке 2.

Как видно из картинки, чтобы прогнозировать будущие состояния временного ряда 1 мы можем также использовать значения временных рядов 2 и 3. Если интересуют прикладные примеры таких рядов - то вот, уровень моря, измеряемый в разных точках показан на Рисунке 3.

Теперь стоит выделить два разных случая “прогнозирования многомерных временных рядов”. В первом у нас на момент формирования прогноза будут доступны данные экзогенных временных рядов только на текущий момент времени и предыстория, то есть t, t-1, t-2, t-n, в то время как данные на индексы прогноза t+1, t+2, t+f (где f - горизонт прогнозирования), неизвестны. Или второй вариант, когда для целевого временного ряда значения на прогнозные индексы неизвестны, но зато есть информация об экзогенных в эти моменты времени. Красочнее всего это можно показать на схеме (см. Рисунок 4).

В первом случае мы имеем дело с классической задачей прогнозирования временного ряда, так как предсказываются будущие состояния. Во втором, решается задача регрессии, однако, поскольку данные упорядочены во времени, у нас есть возможность решать “динамическую регрессию”, которая учитывает ещё и лаговые взаимосвязи в данных. Далее по тексту мы будем говорить только о первом, так как вторая ситуация является частным случаем задачи регрессии. 

P.S. Если хотите послушать про построение динамических регрессий с использованием временных закономерностей, ставьте лайки этой статье, жмите на колокольчик и пишите комментарии. Если наберем 30 классов, то обязательно напишем и про это :)

Как их можно прогнозировать

Ещё ближе к основной теме. Поведение системы из нескольких временных рядов прогнозируется при помощи векторной авторегрессии (VAR). VAR является обобщением идеи авторегрессии для нескольких временных рядов, так что считается классическим выбором для специалиста, занимающимся прогнозированием многомерных рядов. Несколько временных рядов могут включаться в классические модели прогнозирования, такую как, например, ARIMA. В таком случае такие модели будут называться Vector Auto Regressive Moving Average models (VARMA). Для решения данной задачи также применяются рекуррентные нейронные сети, и являются очень популярным инструментом в данной области. Использование “более продвинутых” подходов, например на основе оптимизации того же самого VAR, обычно встречается в научных статьях по ключевым словам “multivariate time series forecasting”.

Попробуем рассмотреть подход обобщения уже известного нам способа прогнозирования одномерных временных рядов на многомерный случай. Как было рассказано в статье Прогнозирование временных рядов с помощью AutoML, временные ряды можно прогнозировать как при помощи классических моделей (AR, ARIMA), так и при помощи регрессионных моделей машинного обучения. Только для использования регрессионных моделей может потребоваться сделать специальное преобразование ряда в матрицу. Для одномерного случая схема преобразования представлена на картинке ниже (Рисунок 5).

Для многомерного временного ряда будет получена следующая таблица (Рисунок 6). Размер скользящего окна и горизонт прогнозирования не меняются по сравнению с предыдущей схемой.

Полученная таблица с признаками может использована как обучающая выборка для модели машинного обучения, например, гребневой регрессии или случайного леса, или любого другого подходящего алгоритма. Таким образом модель будет формировать прогноз, используя в качестве предикторов предыдущие значения как целевой переменной, так и экзогенных временных рядов. Недостатков у концепта приведенного выше можно выделить два:

• Размер скользящего окна, которое используется для всех временных рядов одновременно, может быть неоптимальным. Для одного из рядов может быть достаточно “заглянуть в прошлое” только на 5-10 элементов, чтобы успешно прогнозировать будущее, в то время как для других рядов лаговый сдвиг потребуется делать на сотни элементов;

• Нет никаких гарантий, что используемый экзогенный временной ряд взаимосвязан с целевым.

Бороться с этими проблемами, естественно, можно. И дальше мы рассмотрим как именно. А пока сконцентрируемся на том, как можно всё таки запустить AutoML инструмент для решения задачи прогнозирования многомерного временного ряда.

Как такие ряды прогнозируются в FEDOT (взгляд снаружи) 

Перейдем к примеру с кодом. Итак, задача - используя двадцать пять временных рядов, прогнозировать значения одного из них (целевого) в будущем.

Описание данных

Демонстрацию произведем на данных уровня моря, полученных при помощи модели NEMO (Nucleus for European Modelling of the Ocean). Данная модель позволила подготовить нам датасет с измерениями уровня моря SSH (sea surface height). Временных рядов мы собрали в количестве 25 штук, их расположение на условной карто-схеме можно увидеть на картинке ниже.

Интересующий нас временной ряд выделен на картинке квадратиком. Именно его мы и будем прогнозировать при помощи предыстории параметра в этой точке и при помощи предыстории из соседних. Горизонт прогнозирования - 50 элементов. 

Датасет целиком (под названием SSH) как и код для запуска есть в репозитории pytsbe.

Для этого воспользуемся следующим кодом (наши временные ряды - это numpy массивы, а сам пример запуска есть здесь, версия fedot для эксперимента - 0.6.0):

# Collect dataset with time series to train model
train_data = {}
feature_series = list(train_df['label'].unique())
for feature_ts in feature_series:
  current_ts = train_df[train_df['label'] == feature_ts]
  train_data.update({str(feature_ts): np.array(current_ts['value'])})
  
# Configure AutoML
task_parameters = TsForecastingParams(forecast_length=forecast_horizon)
model = Fedot(problem='ts_forecasting', task_params=task_parameters)
target_series = train_df[train_df['label'] == target_column]
obtained_pipeline = model.fit(features=train_data, 
                              target=np.array(target_series['value']))
# Use historical value to make forecast
forecast = model.predict(train_data)

Выше происходит следующее: формируется словарь с временными рядами, которые будут использованы как предикторы. Как target определяем целевой временной ряд.

obtained_pipeline = model.fit(features=train_data, 
                              target=np.array(target_series['value']), 
                              predefined_model='auto')

Итак, запускается эволюционный процесс, который после определенного числа поколений позволяет получить следующий результат (Рисунок 7).

Выглядит неплохо. На этом пока ограничим наши комментарии и попробуем разобраться что же происходит внутри. 

Как такие ряды прогнозируются в FEDOT (взгляд изнутри) 

Теперь рассмотрим процесс поиска решения. Сначала алгоритму необходимо с чего-то начать процесс эволюции, - с некоторого корректного начального приближения. Такое начальное приближение генерируется автоматически, и получается следующий пайплайн - см. Рисунок 8. 

Выглядит конечно монструозно, но с чего-то надо начинать :) Что же тут происходит. Сначала нам временные ряды подаются каждый в свой “data source” узел (1). Эти временные узлы ничего каждый со своим временным рядом не делают, а передают его дальше. 

Зачем это сделано? - Чтобы можно было подключать к пайплайну новые источники данных, плюс это помогает разобраться с каким именно временным рядом какие преобразования происходят в пайплайне (обратим внимание на названия после слэша, там показаны метки временных рядов, что позволяет однозначно идентифицировать их). Таким образом можно понять, что для временного ряда с названием 0 были применены lagged преобразование и при этом его копия была передана в GLM модель (2). GLM - это обобщенная линейная модель, которая может работать напрямую с временным рядом и ей не требуется его преобразование в траекторную матрицу. Вывод из lagged преобразования передается в модель гребневой регрессии (3). 

Затем предсказания для каждого временного ряда из двух моделей (GLM и ridge) передаются в модель гребневой регрессии (4), ну и финальная модель тоже в данном случае гребневая регрессия. Не переживайте по поводу большого количества моделей гребневой регрессии - это всего лишь начальное приближение, дальше эволюция подберет более оптимальные модели в узлах. 

Затем уже на основе данного начального приближения посредством применения мутаций генерируется начальная популяция из пайплайнов для эволюционного алгоритма. В процессе оптимизации структуры пайплайна AutoML алгоритм может менять операции (модели) в узлах, удалять узлы и ребра, добавлять новые и настраивать гиперпараметры операций. Это значит, что потенциально возможным становится получать следующие структуры (Рисунок 9).

Как видно из Рисунка 9, при необходимости мы можем удалять узлы и целые ветки и таким образом избавляться от временных рядов, которые никак не связаны с целевым. 

Также в процессе оптимизации графа мы можем настраивать отдельно размер скользящего окна для каждого из рядов (регулируется гиперпараметром window size в lagged преобразовании). Это решает проблему с использованием в модели не репрезентативных экзогенных рядов-предикторов.

Ради чего столько мучений?

Для уменьшения ошибки прогноза, очевидно :) Но шутки в сторону, вопрос и правда хороший, и, главное, своевременный, - самое время проверить даёт ли реализованный подход хоть какие-то преимущества. Чтобы убедиться в том, что использование экзогенных временных рядов (и их количество) действительно влияет на ошибку финального прогноза проведем эксперимент. 

Сначала попробуем спрогнозировать временной ряд при помощи автоматически сгенерированного алгоритмом начального приближения. При этом в качестве предикторов будем использовать предысторию целевого временного ряда, а затем будем итеративно расширять количество используемых временных рядов. На последних 50 элементах временного ряда будут сопоставляться прогнозные и действительные значения. Метрика: средняя абсолютная ошибка (MAE). Результаты данной проверки представлены на анимации ниже:

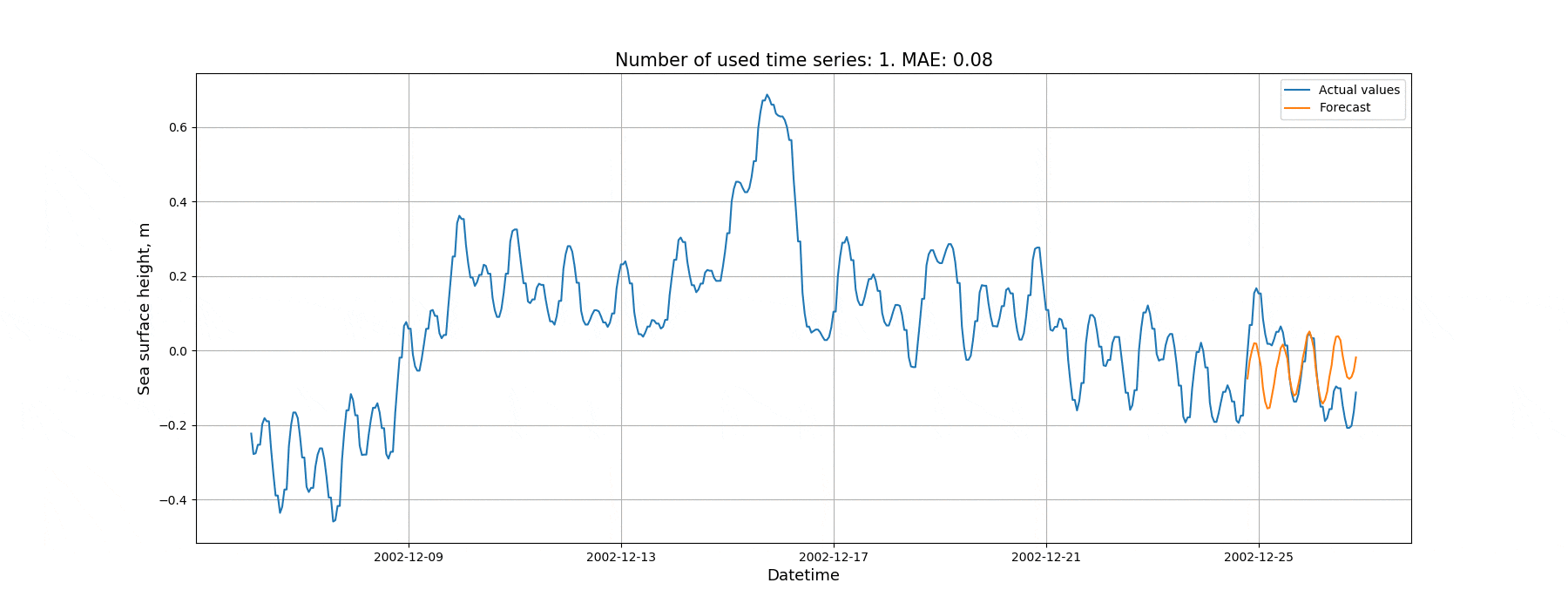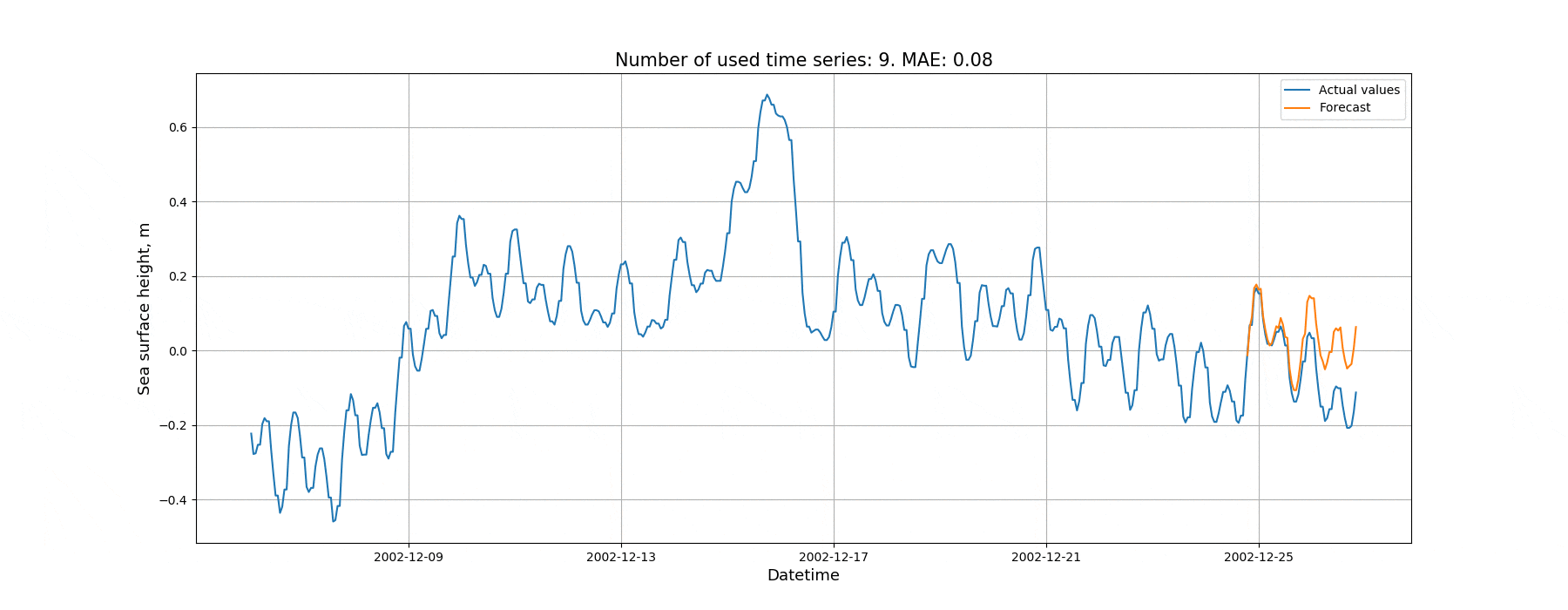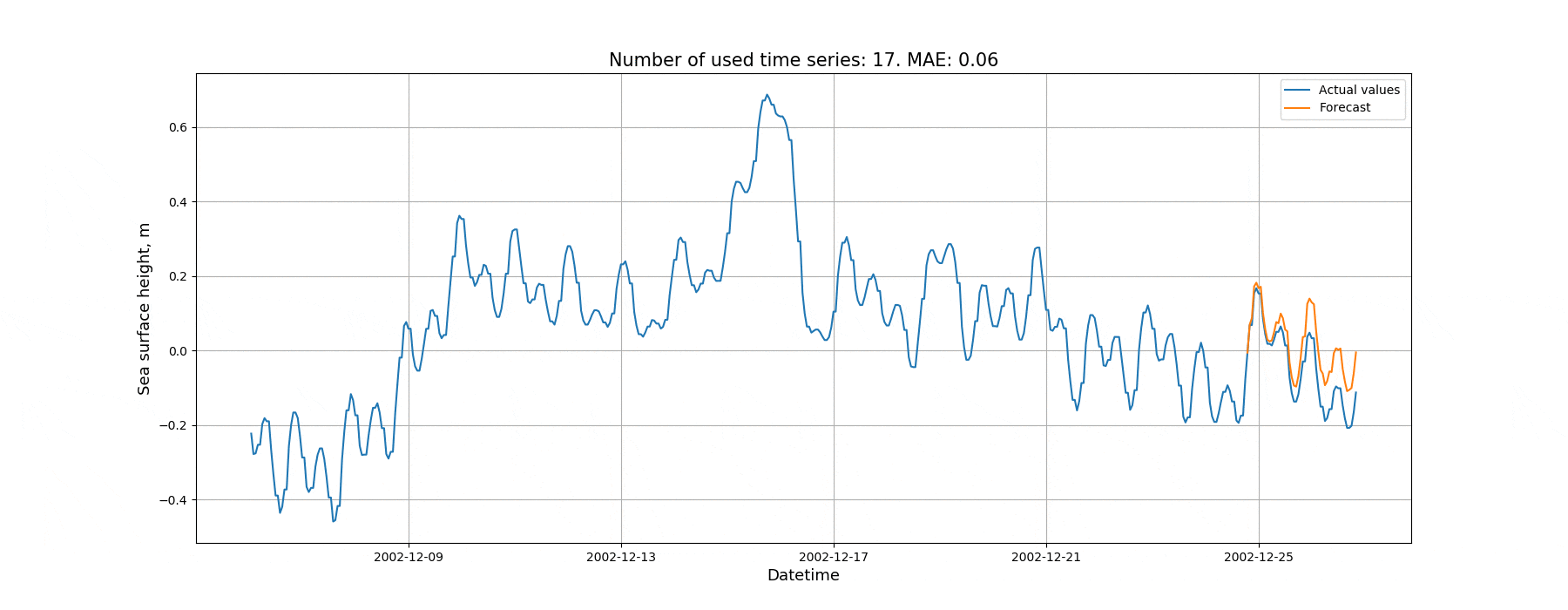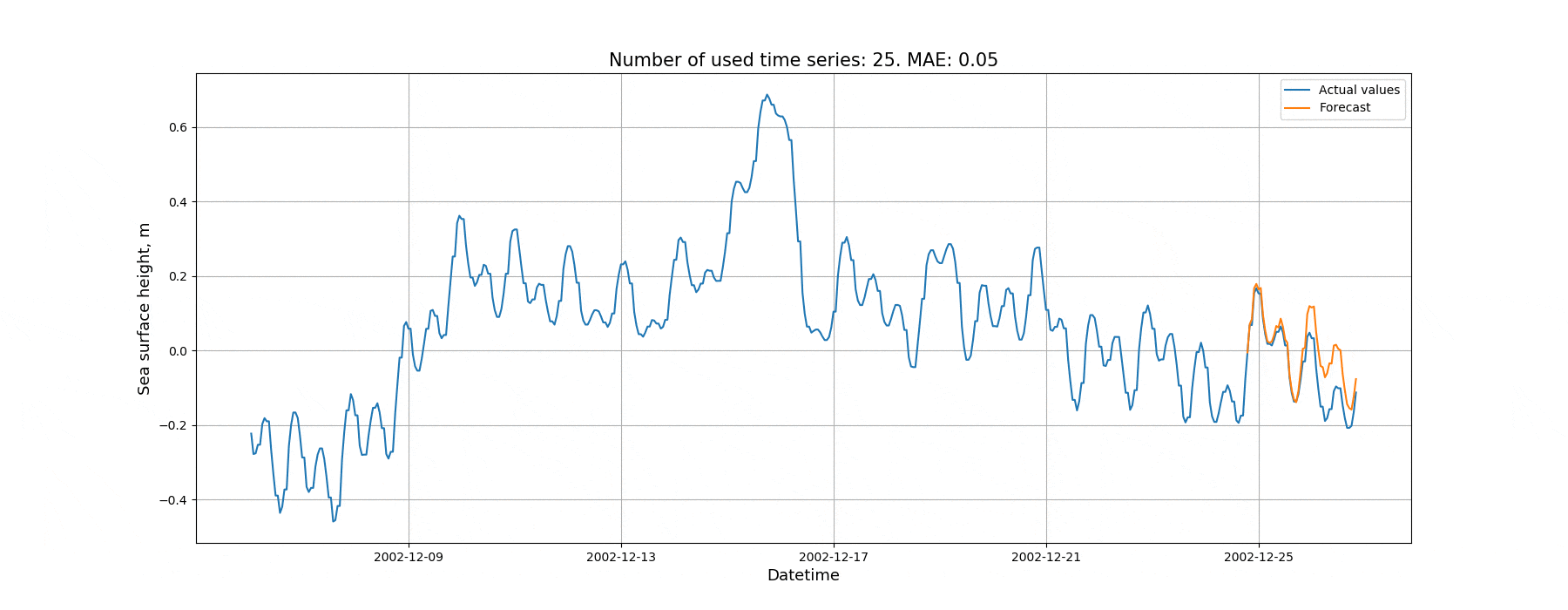
На рисунке 10 показана зависимость ошибки на валидационной выборке от количества рядов.

Как видно из рисунка, количество временных рядов, включаемых в модель, действительно влияет на величину ошибки. Ещё отметим, что в рамках данного эксперимента мы не производили настройку гиперпараметров пайплайна и не модифицировали исходную структуру при помощи эволюционного алгоритма. Когда модель использует множество временных рядов, возможностей для улучшения модели больше в сравнении с простой моделью. Поэтому потенциально после настройки гиперпараметров преимущество более сложной модели может возрасти.

Заключение

В данном посте мы рассмотрели какие есть подходы к прогнозированию многомерных временных рядов. Обсудили как можно прогнозировать такие ряды при помощи AutoML. А после посмотрели подробнее как все устроено в этом AutoML инструменте изнутри. 

Прогнозируйте временные ряды, используйте FEDOT!

Полезные ссылки: 

• Репозиторий open-source AutoML фреймворка FEDOT 

• Репозиторий open-source библиотеки для запуска алгоритмов прогнозирования временных рядов и бенчмаркинга - pytsbe (модуль совсем новый, так что если вы хотите поучаствовать в его open-source разработке - присоединяйтесь!)

• Канал NSS Lab — анонсы наших новых статей и выступлений, посвященных AI/ML

С объяснением концепции того как можно прогнозировать многомерные временные ряды выступал Сарафанов Михаил и команда NSS lab