Введение

Уже не раз на habr затрагивалась данная тема: раз, два.

Я лишь хочу поделиться своей реализацией. Думаю, это кому-то пригодится.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Подготовка

Весь последующий код будет приведён на языке Java

Для начала создадим вспомогательный класс Dot. В нём всего две переменные x и y:

static class Dot {
        float x,y;
        Dot(float x, float y){
            this.x =x;
            this.y = y;
        }
  			
  			@Override
        public String toString() {
            return "x:"+x+" y:"+y;
        }
    }

И класс Vector2. В нём всего две функции: crs (cross) - векторное произведение, scl (scale) - масштабирование вектора.

public static class Vector2 {
        float x,y;

        public Vector2(Dot d1, Dot d2) {
            this.x = d2.x-d1.x;
            this.y = d2.y-d1.y;
        }

        /** Calculates the 2D cross product between this and the given vector.
         * @param v2 the other vector
         * @return the cross product (Z vector) */
        public static float crs(Vector2 v1, Vector2 v2) {
            return v1.x * v2.y - v1.y * v2.x;
        }

        /** Multiplies this vector by a scalar */
        public Vector2 scl (float scalar) {
            x *= scalar;
            y *= scalar;
            return this;
        }
}

Задача 1: определить, касаются ли отрезки.

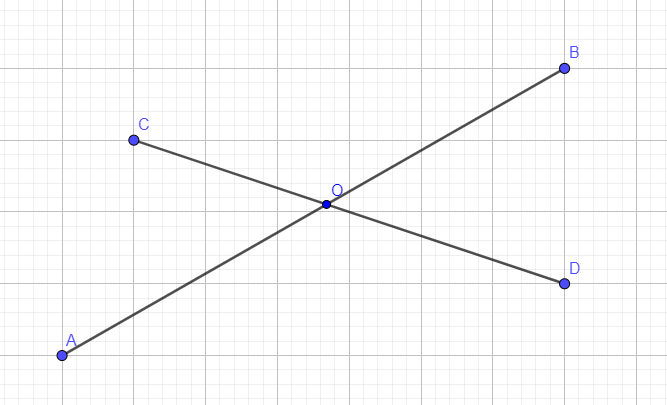
Решение:
Из векторного произведения мы можем узнать, обхо́дим мы вектор по часовой или против часовой. Это поможет понять где находятся точки. Соединим точки A и D, A и C.

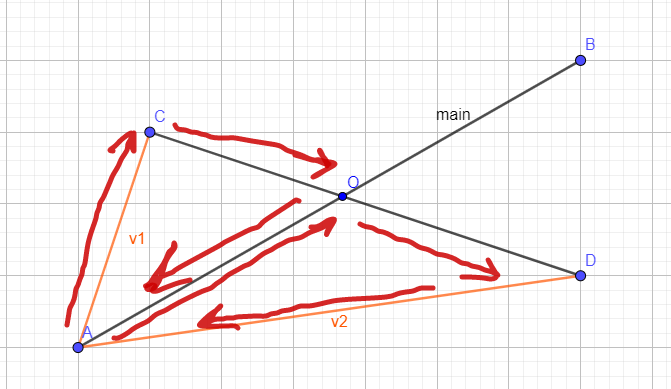
Перемножим вектора main и v2, main и v1. Если полученные произведения имеют разные знаки, значит точки C и D находятся по разные стороны относительно отрезка AB. Назовём такой метод fromDifferentSides:

public static boolean fromDifferentSides(Vector2 main, Vector2 v1, Vector2 v2){
    float product1 =crs(main ,v1), product2 = crs(main ,v2);
    return (product1>=0&&product2<=0 || product1<=0&&product2>=0);
}

Таким же образом необходимо проверить точки A и B относительно отрезка CD. Соединим это в один метод и получится следующее:

public static boolean linesIntersect(Dot a, Dot b, Dot c, Dot d) {
    Vector2 main = new Vector2(a,b);
    Vector2 v1 = new Vector2(a,c);
    Vector2 v2 = new Vector2(a,d);

    if (fromDifferentSides(main,v1,v2)) {
      main = new Vector2(c,d);
      v1 =new Vector2(c,a);
      v2 =new Vector2(c,b);
      return fromDifferentSides(main,v1,v2);
    }
    return false;
}

Задача 2: определить точку касания.

Решение:
Как и в предыдущей задаче определяем, касаются ли отрезки. Если касаются, начинаем определять эту точку. Через подобие найдём длину DO. Коэффициент подобия (k) равен отношению уже известных нам векторных произведений:

//коэффициент подобия
double k = Math.abs(product2 / product1);
if (Float.isInfinite((float) k)) return c;

В третей строчке проверяем пограничный случай. Теперь узнаем чему равно DO. Для этого решим систему уравнений:



DO = CO*k
Подставляем во второе уравнение:
CO*k+CO = CD
CO(k+1)= CD
CO = CD/(k+1)
В итоге:
DO = (CD/(k+1))*k

Теперь создаём вектор CD и уменьшаем его до длинны DO. Но поскольку мы будем его умножать, нужно взять обратное от (k+1)*k:

//вектор DC
Vector2 dc = new Vector2(d, c);

//уменьшаем вектор
dc.scl((float) (1 / (k + 1)*k));

Теперь осталось добавить вектор к точке D:

//добавляем вектор к точке
return new Dot(d.x + dc.x, d.y + dc.y);

Вот и всё! Мы получили заветную точку.

Предупреждаю, данный метод не учитывает некоторые пограничные случаи и вхождение отрезков друг в друга.

Функцию нахождения точки я назвал pointOfIntersection. Привожу полный код на Java:

public class Main {
    public static void main(String[] args) {
        System.out.println(pointOfIntersection(new Dot(0, 0),new Dot(5, 0), new Dot(2, 3),new Dot(2, 0) ));
    }

    public static Dot pointOfIntersection(Dot a, Dot b, Dot c, Dot d) {

        Vector2 main = new Vector2(c,d);
        Vector2 v1= new Vector2(c,a);
        Vector2 v2 = new Vector2(c,b);
        if (fromDifferentSides(main,v1,v2)) {
            main = new Vector2(a,b);
            v1 = new Vector2(a,c);
            v2 = new Vector2(a,d);

            double product1 = crs(main ,v1), product2 = crs(main ,v2);
            if (product1>=0&&product2<=0 || product1<=0&&product2>=0) {
                //коэффициент подобия
                double k = Math.abs(product2 / product1);
                if (Float.isInfinite((float) k)) return c;

                //вектор DC
                Vector2 dc = new Vector2(d, c);

                //уменьшаем вектор
                dc.scl((float) (1 / (k + 1)*k));

                //добавляем вектор к точке
                return new Dot(d.x + dc.x, d.y + dc.y);
            }

        }

        return null;
    }

    public static boolean linesIntersect(Dot a, Dot b, Dot c, Dot d) {
        Vector2 main = new Vector2(a,b);
        Vector2 v1 = new Vector2(a,c);
        Vector2 v2 = new Vector2(a,d);

        if (fromDifferentSides(main,v1,v2)) {
            main = new Vector2(c,d);
            v1 =new Vector2(c,a);
            v2 =new Vector2(c,b);
            return fromDifferentSides(main,v1,v2);
        }
        return false;
    }

    static class Dot {
        float x,y;
        Dot(float x, float y){
            this.x =x;
            this.y = y;
        }

        @Override
        public String toString() {
            return "x:"+x+" y:"+y;
        }
    }


    public static class Vector2 {
        float x,y;

        public Vector2(Dot d1, Dot d2) {
            this.x = d2.x-d1.x;
            this.y = d2.y-d1.y;
        }

        /** Calculates the 2D cross product between this and the given vector.
         * @param v2 the other vector
         * @return the cross product (Z vector) */
        public static float crs(Vector2 v1, Vector2 v2) {
            return v1.x * v2.y - v1.y * v2.x;
        }

        /** Multiplies this vector by a scalar */
        public Vector2 scl (float scalar) {
            x *= scalar;
            y *= scalar;
            return this;
        }

        public static boolean fromDifferentSides(Vector2 main, Vector2 v1, Vector2 v2){
            float product1 =crs(main ,v1), product2 = crs(main ,v2);
            return (product1>=0&&product2<=0 || product1<=0&&product2>=0);
        }
				
      //функция округления
        public static double round(double value, int places) {
            if (places < 0) throw new IllegalArgumentException();
            BigDecimal bd = new BigDecimal(Double.toString(value));
            bd = bd.setScale(places, RoundingMode.HALF_UP);
            return bd.doubleValue();
        }
    }
}

Надеюсь, вам понравилось. Удачи!