Недавно на просторах интернета увидел отрывок из фильма "Двадцать одно". В этом отрывке говорится о том, что парадокс Монти Холла действительно работает!
До сих пор я ничего не слышал об этом парадоксе, но при этом мне никак не верилось в его правдивость, хотя подавляющее большинство говорило обратное. По этому вопросу я смотрел видеоролики, читал статьи, проверял коды программ, но в голове это всё равно никак не укладывалось.
В этой статье будем рассматривать классическую постановку задачи.
В голову приходили разные вопросы: чем отличается дверь без приза по отношению к другой двери без приза, как если мы выбрали именно её? А что если после первой итерации выбора двери к тебе придут Люди в чёрном и сотрут из твоей памяти это первоначальное решение? Куда тогда исчезнут лишние проценты, ведь теперь выбор останется между двумя дверьми?

И вроде бы в расчётах у людей всё сходилось, не к чему было придраться. Тогда для наглядности решил создать google-таблицу, в которой смоделировал 1000 игр на парадокс Монти Холла.
Не долго думая, создал 4 столбца:
столбец A, "Приз за дверью №" - случайное число от 1 до 3 (включительно, конечно);
столбец B, "Выбрали дверь №" - так же случайное число от 1 до 3;
столбец C, "Поменяли дверь" - случайное число от 0 до 1, т.е. либо не меняли дверь, либо поменяли :)
столбец D, "Выиграли" - если выбранная нами дверь совпадает с дверью, за которой находится приз, то значение выигрыша (0 или 1) будет противоположным значению столбца "Поменяли дверь", иначе значение выигрыша будет таким же, как и значение в столбце "Поменяли дверь". Это логично.
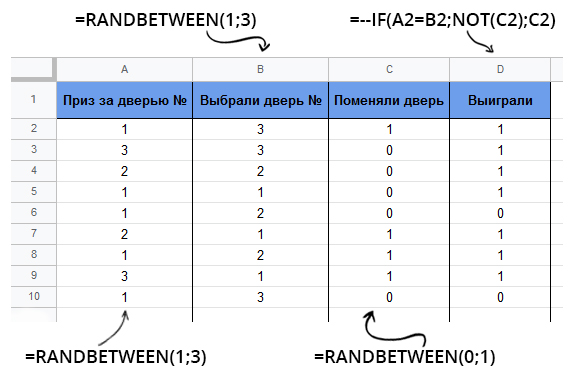
После прямых подсчетов получилась так, что в суммарных полях "Поменяли" и "Не меняли" было соотношение приблизительно 50 на 50. В суммарных полях "Выиграли" и "Проиграли" соотношение было тем же (условно).

Такие соотношения с каждым глобальным прогоном по моделированию 1000 игр сохраняются. Но где же тогда 66% выигрышей?
Посчитаем теперь суммы для всевозможных сочетаний событий по всем играм.

Суммарное поле "Выиграли, когда поменяли" практически в 2 раза превосходит суммарное поле "Выиграли, когда не меняли" по значениям.
То есть получается, что меняя дверь, мы увеличиваем свои шансы на победу в 2 раза? НЕТ! Дело в том, что если мы уже выиграли, то нам не нужны дополнительные условия, меняли ли мы дверь или нет.
Проблема этого парадокса заключается в том, что ответ на задачу поставлен с ног на голову: причина и следствие меняются местами!
Вместо "Если он поменяет дверь, то с вероятностью 2/3 выиграет" нужно говорить: "Если он выиграл, то с вероятность 2/3 менял дверь". Чувствуете разницу? - она диаметрально противоположная. И вы можете менять дверь или не менять - суть заключается в том, что шансы на победу составляют 50 на 50.
Вместо "Мы меняем дверь и выигрываем в 2 раза чаще, чем не меняем дверь" нужно говорить: "Мы меняем дверь и выигрываем в 2 раза чаще, чем не меняем дверь и выигрываем".
Неправильные умозаключения рождают такие парадоксы. Но интуитивно мы понимаем, что здесь что-то не так :)
Приведу еще пару примеров.
Представьте, что ведущий предлагает на выбор 2 двери, только за одной из которых находится приз. Очевидно, что вероятность выбрать правильную дверь составляет 50%? А теперь ведущий внезапно открывает 3-ю дверь, за которой нет никакого приза. Неужели вы думаете, что из-за этого у вас станет меньше шансов на победу? Да пусть он откроет хоть 100 дверей, шансы от этого не поменяются.
А если изначально будет миллион дверей, разве вы проиграете 1-2 раза в миллион игр, меняя дверь? Очевидно, что нет. И проиграете вы примерно столько же, сколько и выиграете. Просто если выиграете, то скорее всего вы меняли дверь, именно так - в обратную сторону это не работает!
Вот что я хотел донести до вас! Надеюсь, у меня это получилось, так как это мой дебют.
Больше доверяйте своей интуиции! Всем удачи!
Комментарии (61)

Dasdy
12.10.2021 14:53Изначально в задаче спрашивается, есть ли разница в вероятности при смене двери или нет, т.е. мы говорим об условной вероятности. Поскольку вы в первом эксперименте это условие разыгрываете с вероятностью 50%, то и на выходе у вас результат неправильный. А вот на втором изображении как раз "реальный результат" - поскольку мы обычно расцениваем вероятности с точки зрения того, что произойдёт, если игрок всегда будет придерживаться целевой стратегии.
Если взять, например, рулетку, то вероятность выиграть при ставке на красное чуть меньше 50%. С вашим подходом игрок бы случайным образом ставил на позиции по всему полю, и вероятность выигрыша была бы существенно меньше.

Reflector
12.10.2021 15:00+5Выбирая одну дверь из трех вероятность угадать дверь с призом равна 1/3. Если выбрана дверь с призом, то после смены получим дверь без приза. Если в двух оставшихся случаях выбрана одна из дверей без приза, то она поменяется на дверь с призом, что дает уже вероятность равную 2/3.

averkij
12.10.2021 15:01+3Вместо «Если он поменяет дверь, то с вероятностью 2/3 выиграет» нужно говорить: «Если он выиграл, то с вероятность 2/3 менял дверь». Чувствуете разницу? — она диаметрально противоположная.
Не чувствую. Как, например, я могу сказать что выиграл или нет, если я еще не выбрал дверь.
Выбранная мной дверь с вероятностью 2/3 пустая, потому что я выбирал из трёх. В этот момент было бы здорово переключиться на противоположный вариант, но я не могу этого сделать, потому что альтернативных вариантов два. Затем ведущий убирает неправильный вариант и теперь я могу гарантированно поменять результат и выбрать выигрышный вариант с той же вероятностью 2/3.
Reflector
12.10.2021 15:03Выбрав дверь с призом ничего кроме дверей без приза не остается, а выбрав дверь без приза остается только дверь с призом, т.к. вторую дверь без приза открывают.

sunsexsurf
13.10.2021 11:29А вот нет же.
предположим, вы выбрали дверь из трёх и за вашей дверью приз. Одна беда: вы этого не знаете. И тут ведущий говорит: «что ж, повременим с решением, май френд. я открываю третью рандомную». Значит ли это, что за вашей тоже пусто? Или что за вашей приз? Да вот хрен знает. Он просто открыл третью дверь. Глобально приз как лежал за вашей, так и лежит.
Ну или да, ткните, где я не прав в рассуждениях.

Reflector
13.10.2021 11:46Ведущий не открывает рандомную дверь, он открывает дверь без приза из-за чего вероятность выбора неправильной двери уменьшается.

sunsexsurf
13.10.2021 14:28да, естественно рандомную, но такую что она а/ не наша и б/ без приза. Либо открыть все, которые попадают под условие выше. Просто можно же растянуть задачу на N дверей же и открыть после нашего выбора не 1 дверь (при выборе из трех), а N-минус 2 двери. Но и тогда я не понимаю, почему вероятность всех дверей суммируется в одну неоткрытую и не нашу дверь, а не делится поровну.

unibasil
13.10.2021 16:36+1Когда вы выбираете дверь, всё множество в n дверей делится на два множества - вашу дверь и остальные двери в количестве n-1. Вероятность приза за вашей дверью 1/n, за остальными дверями (n-1)/n. Открывая двери, ведущий начинает уменьшать второе множество, при этом общая вероятность приза в этом множестве не меняется (потому что приз не перемещается, он уже либо у вас за дверью, либо в этом множестве - но с исходными вероятностями!). Сократив второе множество до одной двери, вы получаете, что вероятность приза за ней (n-1)/n против вероятности 1/n за вашей дверью. Ситуации "50 на 50" вообще не возникает ни на каком этапе (при n >= 3), это чистая иллюзия.

sunsexsurf
13.10.2021 16:38+1а, вот. Вот так (уменьшение множества) становится более ясно про "концентрацию" вероятностей в другие двери, кроме моей. Спасибо вам.

unibasil
18.10.2021 08:07+1Кстати, сегодня я узнал о существовании другого парадокса, про конверты, и вот для него у меня самого уже нет ясного понимания, в чём подвох, даже с приведённым объяснением. Всё-таки вероятности — это сложно и контринтуитивно...

Alexandroppolus
18.10.2021 08:16+1Там суть в том, что невозможно иметь какую-то равномерную вероятность на бесконечном интервале. На конечном отрезке - можно. Парадокс возникает, когда предполагается, что такая вероятность на бесконечном интервале есть.

sunsexsurf
18.10.2021 10:24вот тут на Хабре читал статью про чистку данных и там интересно про резервуарный семплинг - это то, о чем вы говорите? Ну и да, а если отрезок - это часть бесконечного интервала, но сам отрезок бесконечно большой? Или вы хотите сказать, что когда он большой, но конечный, то все ок, а когда именно что бесконечный - то начинаются проблемы?

unibasil
13.10.2021 16:15Вы не знаете, лежит ли за вашей дверью приз или нет. Вы знаете только вероятность, что он там лежит. И эта вероятность фиксируется в момент первого выбора. После этого, какие бы манипуляции с дверьми ни проводились (кроме открытия вашей), эта вероятность остаётся той же.
> Глобально приз как лежал за вашей, так и лежит.
Глобально он там лежит с вероятностью 1 к общему количеству дверей. То есть если при миллионе дверей он там скорее всего не лежит (если, конечно, игра не проводится на Плоском мире, где, как известно, шанс "один на миллион" выпадает в 9 случаях из 10 ;), то при исключении лишних дверей он там вряд ли появится, чтобы его можно было забрать с вероятностью 50 на 50.
sunsexsurf
13.10.2021 16:33ну то есть, довольно занятная картина: моя вероятность - 1/3, а для человека, который только что подошел и тупит на две двери вместо трех - 1/2. Хотя глобально ситуация вообще не менялась.

unibasil
13.10.2021 16:43Ваша вероятность 2/3, если вы поменяете выбор. А у только что подошедшего всего лишь 1/2. У вас больше шансов, не находите? ;)

sunsexsurf
13.10.2021 16:49это если поменяю... ))
Ну и да, ок, поменял. Теперь мы вдвоем таращимся на одну и ту же дверь. При этом моя вероятность - 2/3, а его - 1/2. А дверь одна и та же.

GraDea
13.10.2021 23:58+1Можно расширить эту ситуацию:
Представим, что было сто дверей и сто игроков каждый со своей дверью. Только у этих ста чуток иные правила: они видят только свою дверь. И вот вы таращитесь втроем - каждый со своей вероятностью)
В этой ситуации у тебя больше всего информации, у одного из сотни меньше всего.

unibasil
14.10.2021 07:23Но вы-то знаете, что двери на самом деле разные, а он не знает, для него они одинаковые. Для него шанс будет "50 на 50", для вас 1/3 на 2/3. У вас есть дополнительная информация, которую подогнал добрый ведущий, исключив лишние двери.

Alexandroppolus
12.10.2021 15:08Вместо "Если он поменяет дверь, то с вероятностью 2/3 выиграет" нужно говорить: "Если он выиграл, то с вероятность 2/3 менял дверь". Чувствуете разницу? - она диаметрально противоположная. И вы можете менять дверь или не менять - суть заключается в том, что шансы на победу составляют 50 на 50.
Полагаю, лучше сформулировать так: сначала игрок решает для себя, будет ли он менять дверь. И решив, что будет, он на момент старта игры (до честного рандомного размещения приза) имеет шанс 2/3 на победу.

Alexandroppolus
12.10.2021 15:25А вот когда игрок изначально не определился со стратегией, выбрал дверь и все рандомы позади, то уже имеем совсем другой расклад для вероятности выигрыша: 1, если он удачно выберет стратегию, и 0, если неудачно. Видимо, об этом хотел сказать автор.

unibasil
12.10.2021 15:11+1По-моему, самое интуитивно понятное (для меня точно) объяснение такое: в игре 10 дверей и на втором шаге ведущий открывает 8, оставляя всё тот же выбор из 2 дверей, направляя мысли играющего на выбор "50 на 50". Но шанс на выигрышную дверь в первоначальном выборе будет 1 к 10, и он никак не поменяется после открытия остальных дверей. Поэтому поменяв выбор двери, мы меняем этот шанс с 10% на 90%.
> А если изначально будет миллион дверей
Тогда ведущий должен открыть 999998 дверей, тем самым сведя выбор якобы к тем же самым 50 на 50. Но тут уже очевидно, что первоначальный выбор был выигрышным с шансом всего один на миллион, и поменяв дверь, мы практически гарантированно выигрываем.

hwb
12.10.2021 15:16+14Если уж играться с табличками, то не обязательно при этом использовать тысячи рандомных игр - достаточно просто заполнить её всеми возможными комбинациями - тогда сразу увидим, какова вероятность выигрыша в случае замены и не-замены двери.


Biga
12.10.2021 16:24+1С этим надо быть аккуратнее, потому что в такой табличке все варианты (строки) должны быть независимы друг от друга, иначе получится вовсе не то, что вы хотите. А определить независимость событий - не такой простой вопрос, как кажется.

hwb
12.10.2021 18:14+1Каждая строчка в таблице представляет собой уникальное начальное условие (где был приз и какую дверь выбрали) и два варианта исхода в зависимости от решения о смене двери. Для наглядности и экономии места я не стал делать отдельную строку для каждого исхода, а расположил их в колонках. Как мне кажется - строки вполне независимы друг от друга. Если объясните поподробнее, в чем я ошибся - буду крайне признателен.

Biga
12.10.2021 20:35Я не говорю, что вы ошиблись. Всё правильно.
Просто есть другие задачи, которые легко и непринужденно решаются такой табличкой, но неправильно, потому что события получаются зависимыми, хотя это и не очевидно.

Cykooz
12.10.2021 17:11+4Можно вообще не менять положение приза, т.к. это ни на что в итоге не влияет. Т.е. достаточно рассмотреть первые три строки из вашей таблицы.

hwb
12.10.2021 18:02Все верно, так и хотел сделать сначала, но для наглядности решил привести полностью все возможные варианты, чтобы уж точно не было подозрений в какой-либо подтасовке )

old_gamer
12.10.2021 15:26+9Мне вот такое наглядное объяснение помогло в свое время. Представте, что вы играете в эту игру с другом. Вы никогда не меняете дверь, а друг меняет всегда. Тогда вы выиграете в 33% случаем (вы выбираете одну дверь из 3х, и больше ничего не влияет на ваш выбор), и проигрываете в 66%. Но когда вы проигрываете, ваш друг выигрывает.

censor2005
12.10.2021 15:57+1Спасибо, действительно, так проще будет объяснить человеку, который ранее не сталкивался с этим парадоксом!

old_gamer
12.10.2021 16:19Упс, забыл упомянуть, что дверь вы выбираете одну и ту же всегда вместе. Просто вы держите ее до конца, а друг меняет )

Apxuej
12.10.2021 16:29+2"Представьте, что ведущий предлагает на выбор 2 двери, только за одной из которых находится приз. Очевидно, что вероятность выбрать правильную дверь составляет 50%? А теперь ведущий внезапно открывает 3-ю дверь, за которой нет никакого приза. Неужели вы думаете, что из-за этого у вас станет меньше шансов на победу? Да пусть он откроет хоть 100 дверей, шансы от этого не поменяются."
Автор, в том то и дело, что после первичного выбора шанс на победу не меняется. У Вас было 50% победы и остальные двери на это не влияют. Единственный вариант, когда Ваш шанс на победу вырастет, если ведущий откроет вторую дверь, тогда станет понятно что именно за вашей дверью приз.
Приведу самую понятную аналогию изначальной проблемы - мне очень помогла. Дверей 10^10^10^10. Вы выбираете одну. Ваш шанс на выигрыш исчезающе мал, фактически 0. Далее ведущий открывает все остальные двери кроме одной. Так как Вы абсолютно уверены, что за вашей дверью ничего нет, то за той, которую оставил ведущий практически 100% будет приз. Если же пришёл Агент Джей и стёр вашу память, то шансы вновь 50% на 50%, потому что у Вас нет подсказки от ведущего. Дополню ещё, что та дверь которую Вы изначально выбрали особая - она не участвует в исключающем процессе со стороны ведущего.
P.S. Автор, признайтесь, Вы решили потроллить хабр?

sunsexsurf
13.10.2021 11:22А вот это, кстати, отличное объяснение про «стёрли память» и «дверь не участвует». То, что дверь не участвует - это, по сути, некоторая подсказка. И чем больше дверей, тем подсказка сильнее

Akina
12.10.2021 16:47Получаемые 50% есть ни что иное как вероятность получения определённого (например, единицы) значения в колонке "Поменяли дверь". Попробуйте для эксперимента сделать там не равновероятное значение 0/1 - и общая вероятность выигрыша тоже начнёт ползать за устанавливаемым процентом вероятности.

aamonster
12.10.2021 16:48+2Прекрасная иллюстрация к эффекту Даннинга-Крюгера! :-)

Daddy_Cool
12.10.2021 23:48Вы суровы! ) Хотя… я как-то на заре человечества узнал, что такое векторный лапласиан и окрыленный этим знанием стал кому-то доказывать, что это всего лишь оператор Лапласа примененный к каждой компоненте вектора. О криволинейных координатах я и не подумал. Потом было стыдно.

vvadzim
12.10.2021 18:35М-да....
Давайте так сыграем - вы не будете менять никогда, а я буду менять всегда. Кто из нас будет чаще выигрывать? Сможете проверить это в экселе?
ПС
Вы будете просто выбирать, какую одну из трёх дверей вы хотите открыть для себя. Шансы угадать - 33.3%. То, что будет вытворять на сцене ведущий, на содержимое за вашей дверью никак не повлияет. Он может открывать двери в любом порядке, вы выигрываете только если за вашей одной дверью авто. Вы свой выбор сделали.
Я же буду выбирать, какую одну из трёх дверей НЕ открывать. Я буду выбирать, какие ДВЕ двери открыть, и просто укажу на ту, какую нужно оставить закрытой. И снова, порядок открытия дверей уже не важен. Одну из двух оставшихся ведущий откроет сначала, вторую после. Ну не одновременно, ну и ладно. То, что ведущий выбирает, в каком порядке открывать те две двери, никакой роли не играет - они обе будут открыты. Мои шансы выиграть - 66.7%
ППС
В задаче просто нагородили кучу слов чтобы заморочить голову. На самом деле в задаче вопрос такой: кто будет выигрывать чаще, тот кто открывает только одну дверь, или тот кто открывает две?

TiesP
12.10.2021 18:51+1Спасибо за статью, жаль что её заминусовали. Мне стало более понятно объяснение этого парадокса… в основном благодаря комментариям :)

Ad_fesha
12.10.2021 19:18+2Хабр по мойму - один из немногих сайтов, где комменты, зачастую, могут оказаться ценнее самой статьи. Это даже у самой Хабры где-то написано=)

alex103
13.10.2021 06:41Это тот случай когда математика "не работает".
За статью -1, за статью с комментариями +1, а в сумме получается вовсе даже не 0!
(по моему)

jetcar
12.10.2021 19:21+2Оказывается я настолько стар, что появляются темы про которые уже давно все разобрались и железно доказали как оно работает, а главное обьяснили даже самым тупым. Видимо следущее поколение подросло и решило пошатнуть основы, снова :D

Enverest
12.10.2021 20:40Представьте что условие задачи — выбрать дверь без приза. И пусть будет изначально 100 дверей. Т.е. выбранная дверь будет без приза будет 99%. Убирают остальные двери кроме вашей и ещё одной. И тут вопрос — будете ли вы менять дверь? У вас ведь уже пустая дверь 99%.

oxx
13.10.2021 12:13Собственно, чтобы понять парадокс нужно было понять только один факт: ведущий знает, где приз и всегда откроет только ту дверь, за которой приза нет. Это и есть условие, которое меняет вероятность, а вовсе не количество закрытых дверей. Это важно.
Представьте, что ведущий предлагает на выбор 2 двери, только за одной из которых находится приз. Очевидно, что вероятность выбрать правильную дверь составляет 50%? А теперь ведущий внезапно открывает 3-ю дверь, за которой нет никакого приза. Неужели вы думаете, что из-за этого у вас станет меньше шансов на победу? Да пусть он откроет хоть 100 дверей, шансы от этого не поменяются.
А вот это уже непонимание теоремы Байеса.



Ad_fesha
Представьте, что изначально у Вас 1 млн дверей. Вы выбрали дверь, и в этот момент отрываются все двери кроме 2-ух (Вашей и еще одной).
Шанс, что Вы изначально выбрали дверь с призом равна 1/млн. Шанс что Вы выбрали дверь без приза 99.9...%. Если Вы меняете дверь - шанс, выиграть увеличивается. У Вас в задаче не 2 двери, а 3. Суть примерно та-же, шансы разные...
aveS0me Автор
Ладно, понятно, я не прав был, как себя заминусовать :)
Ad_fesha
Минус Вам не ставил
Не смотря на минусы, думаю многим, кто был не знаком с парадоксом, смогут с ней получше ознакомиться =)
Главное не ставьте на себе крест. Возможно следующая статья, будет более продуктивной
aveS0me Автор
Спасибо) Рассматривал парадокс, как будто с позиции до и после, общей картины не видел, хотя комментарии с примерами на большое количество дверей видел часто, но все равно не доходило. Сейчас понял всё)
sunsexsurf
Хорошо. Но ведь можно рассмотреть эту историю иначе. У вас миллион дверей. Шанс, как вы заметили, 1/1млн.
Теперь открываются все двери, кроме двух.
В этот момент, даже выбирая ту же самую дверь, я делаю свой выбор по второй раз, по сути, нет? И выбираю (пусть даже ту же самую), но уже из двух, разве нет? Почему вероятности не пересчитываются? Почему они не обнуляются после первого хода?
unibasil
А почему вероятности должны пересчитываться? У вас две двери, на изначально выбранной вероятность 1 на миллион так и остаётся (с чего ей меняться? если там не было приза, от открытия остальных дверей он вдруг за ней не появится), зато все вероятности с открытых ведущим дверей суммируются на вторую дверь. То есть перед вами остаются две двери, но они совсем не одинаковые.
sunsexsurf
Ну, например, с того, что мы до конца не знаем, есть ли приз за нашей дверью. И открывают третью для нас не потому что мы выбрали пустую, а просто так (как я понял). И вот тут для меня совсем не ясно, почему вероятности приза суммируются в _не нашу_ дверь, а не поровну?
unibasil
Потому что приз никуда не перемещается. Состояние за уже выбранной дверью не меняется. Там не может появиться приз, если его не было, и исчезнуть, если он там был, даже если остальные двери без приза открыты. Поэтому вероятность найти приз за выбранной дверью остаётся той же самой, какой была с самого начала, один на миллион.
sunsexsurf
Так. Вот тут момент интересный. Есть 3 двери. P(win prize) = 1/3, так? Приз где-то лежит. Мы его не переносим никуда. Выбираем дверь. После фиксации получаем вероятность приза за каждой дверью - 1/3. Еще раз: у каждой двери вероятность - 1/3. Открывается третья дверь. Она без приза, естественно. Итак, почему же в этот момент _у нашей двери_ вероятность остается 1/3, а у соседней - вырастает до 2/3? Из-за чего в этот момент соседняя дверь становится такой особенной?
Ad_fesha
На примере в 3 двери, возможно понять сложнее.
Представьте что изначально их не 3 а 100 или более. Вы, выбрав дверь одну из 100, имеете шанс в 1 % победы. Как только открываются другие двери, Ваш шанс не меняется т.к. изначальные условия не поменялись.
Грубый пример для наглядности. У Вас 100 попыток, где Вы всегда выбираете дверь с номером 1. После выбора Вашей двери - открываются ВСЕ двери. Их открытие НЕ влияет на повышение шанса, т.к. это происходит после выбора 1к100, соответственно из 100 попыток у Вас будет только одна победа. Соответственно, если после выбора Вашей двери, открываться будут Все кроме двух дверей, на Ваш шанс победы это тоже, никоим образом не скажется. (т.е. будут открываться все двери или будут открываться все двери минус х дверей, не влияет на повышение шанса выигрыша у Вас)
По причине повышения шанса, у другой двери, мне кажется, разжевывать уже не нужно=)
unibasil
Иначе можно было бы изобрести оригинальный способ практически всегда выигрывать в лотереи -- дожидаемся, пока свои билеты проверят все остальные неудачники и с вероятностью 50 на 50 выигрываем джекпот. ;)
sunsexsurf
скорее, "дожидаемся, когда у противника не осталось кораблей и врисовываем однопалубник на пустое место". Или "дожидаемся, какую дверь выбрал человек и кладем приз за другую".
unibasil
Другое дело, если вам перед вторым выбором стёрли память и вы не знаете, какую дверь первоначально выбрали. Тогда перед вами действительно две одинаковые двери, за одной из которых приз. Но в этом случае и действие "поменять выбор двери" теряет смысл, вместе с сутью самого парадокса. ;)
Alexandroppolus
Нет! Именно что нет никакого второго выбора. Выбор "поменять или не поменять дверь" вы для себя сделали перед игрой. И парадокс М-Х именно о той вероятности, которая была вычислена после выбора стратегии, но до начала игры.