Частичные пароли: история о том, как задёшево вывести из себя пользователя и/или как вставить палки в колёса кейлоггерам.
Здравствуйте!
Что такое частичный пароль? Каковы достоинства и недостатки их использования в процессе аутентификации? В статье подробно рассматриваются математические основы, технические детали и практика применения частичных паролей. Предлагается порассуждать об их месте в современных цифровых системах.
Начнем, как принято, с определения: частичные пароли (от англ. partial passwords, pps) – это один из методов аутентификации, при котором у пользователя просят ввести некоторый случайный набор символов из пароля вместо полного пароля. Например, запрос может выглядеть следующим образом: «Пожалуйста, введите 2-й, 3-й и 6-й символ!». Я с удивлением обнаружил, что pps широко распространены на страницах многих зарубежных компаний, особенно в финансовом секторе. Однако, как пользователь, до недавнего времени я не был знаком с такой модификацией классической парольной защиты, но она показалась мне довольно занимательной. Источников на русском языке мне найти не удалось, поэтому я решил взять на себя ответственность рассказать читателям о pps, сопровождая материал пояснениями, формулами и картинками, помогающими понять суть вопроса. Приятного чтения!
Содержание:
Математический теорминимум
Контекст и мотивация к использованию pps
Детали реализации pps
Атаки на pps. Математические модели и некоторые численные результаты
Модельный пример реализации pps на языке python
Обсуждение и выводы
1. Математический теорминимум, иллюстрированный
Предполагая, что этот текст может быть интересен широкому кругу лиц, считаю необходимым привести некоторые элементарные факты из комбинаторики и теории вероятности, которые будут активно использоваться в статье.
(Если Вы без труда отличаете размещение без повторений от сочетаний с повторениями и помните, чем отличаются независимые события от несовместных, то можете пропустить этот раздел)
Много букв, еще больше картинок
Факториал натурального числа n
Число перестановок без повторений из n
Найдем количество всевозможных способов расставить n различных элементов по n упорядоченным позициям. Их штук. Действительно, на первую позицию мы можем поставить любой из n элементов, на вторую —
оставшийся и так далее, на последнюю,
-ую позицию, остается лишь один оставшийся элемент.
Число перестановок с повторениями из n для m типов, :
Вновь имеем n упорядоченных позиций. В отличие от предыдущего случая, рассматриваются m различных типов элементов, в каждом из которых по элементов,
). Внутри своего типа элементы неотличимы друг от друга. Найдем число вариантов перестановки этого набора элементов. Расположим произвольным образом все n элементов по n упорядоченным позициям. Теперь представим, что мы можем отличить все элементы друг от друга внутри каждого класса. Например, наклеим на каждый элемент ярлычок с его порядковым номером от
до
в соответствии с тем, как они были только что расставлены. Теперь найдем число их перестановок. Это
, ведь ярлычок помогает отличить каждый элемент друг от друга. На самом же деле нас интересуют перестановки различных типов элементов, ярлычки имеют вспомогательную функцию. Рассмотрим теперь первый тип: любые из
перестановок, где меняются местами лишь элементы первого типа, неотличимы друг от друга ( фактически, меняются местами одинаковые элементы с разными ярлычками). Перестановок ярлычков среди элементов первого типа
штук, то есть только каждая
-ая перестановка из
уникальна, а всего перестановок становится
. Проводя аналогичные рассуждения для второго, третьего, ...,
-ого класса, получаем
перестановок. Это и есть количество перестановок с повторениями. При выборе
(каждый тип имеет только по одному элементу) получаем перестановку без повторений
.
Число размещений из n по k без повторений
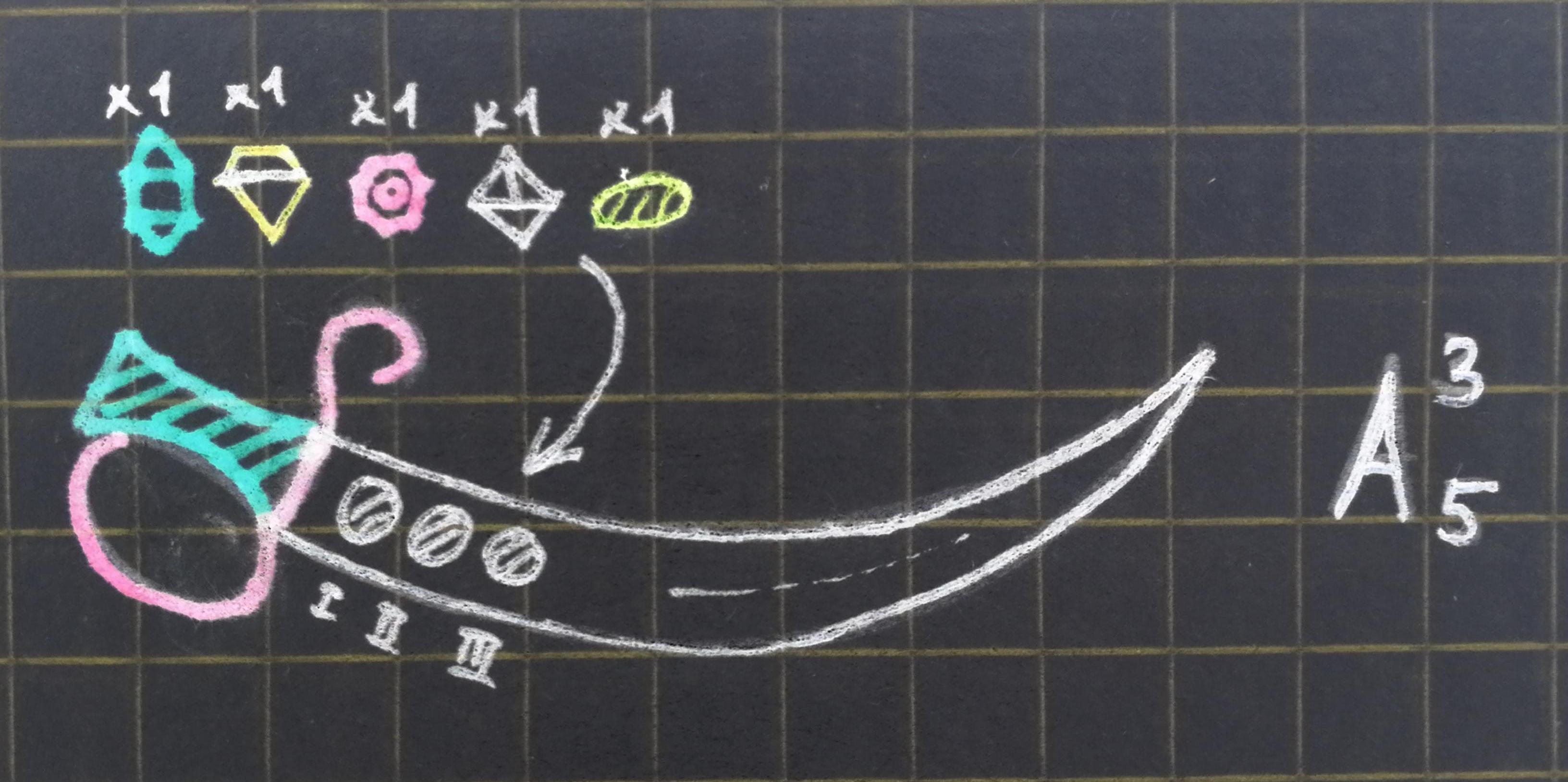
Найдем количество способов разместить из
различных элементов по
упорядоченным позициям. Оно равно:
. Справедливы те же рассуждения, что и в случае перестановок без повторений, но в распоряжении мы имеем уже
элементов, так что у нас даже для последней позиции остается свобода выбора (
вариант).
Число размещений из n по k с повторениями
Имеем упорядоченных позиций и
типов элементов, притом элементов каждого типа имеем в достатке, хотя бы по
штук. На любую из
позиций можем поставить любой элемент одного из
типов. Получаем
размещений.
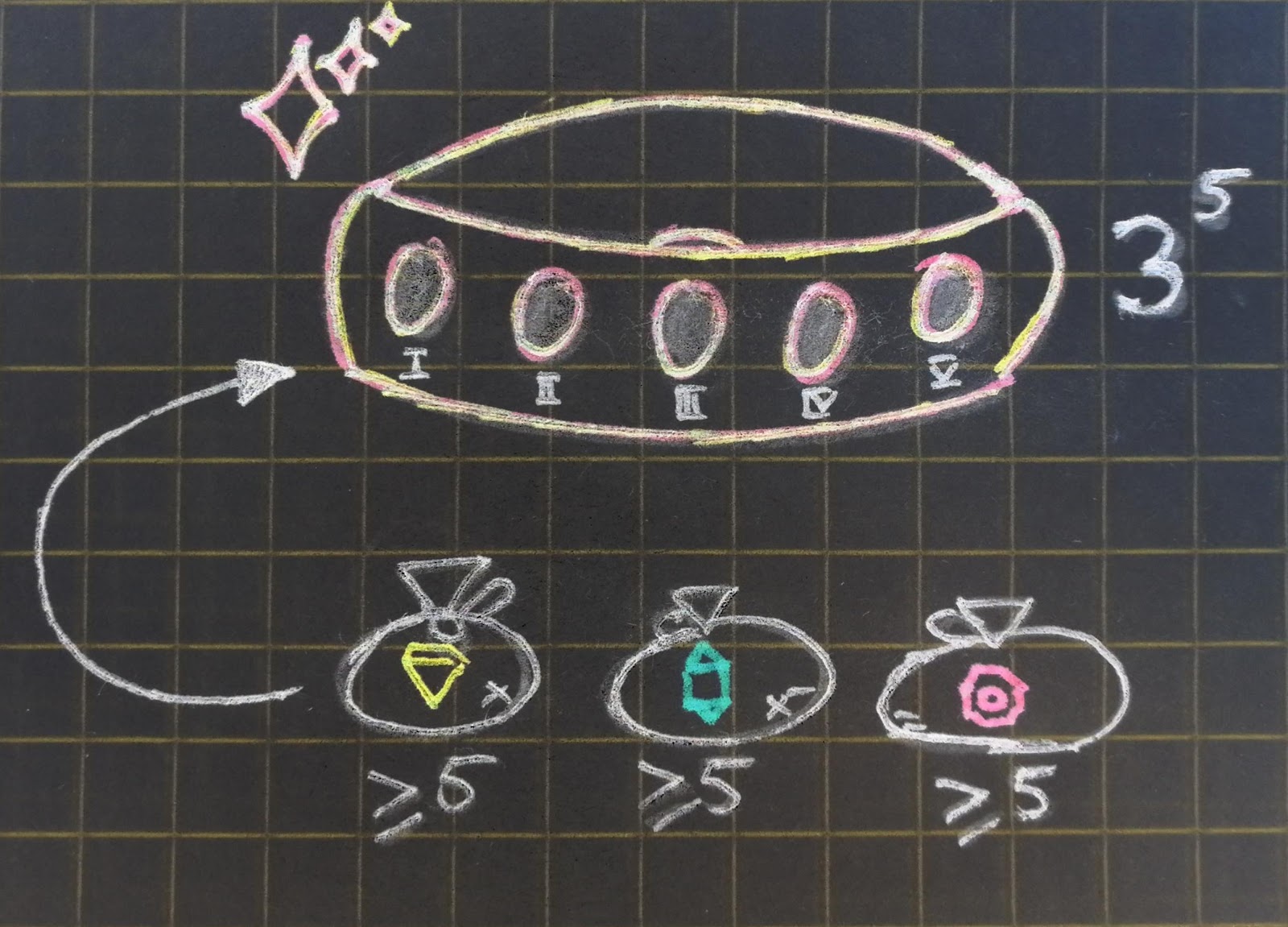
Число сочетаний из n по k без повторений
В случае сочетаний изменим постановку задачи. Рассмотрим некоторое множество из различных элементов. Найдем число способов достать из него
элементов, считая, что их порядок нам не важен. Иными словами, сколькими способами мы можем выбрать неупорядоченный набор из
элементов из неупорядоченного набора из
различных элементов (тогда после выбора
элементов останутся
неупорядоченных элементов). Таким образом, мы легко свели вычисление к случаю размещений с повторениями c двумя типами: в первом типе имеем
элементов (мы их выбираем), а во втором —
(мы их оставляем). Отсюда находим, что число сочетаний из
по
без повторений равно
Очевидно, что . Оставим доказательство этого простого утверждения читателям в качестве упражнения (ну а как без этого).
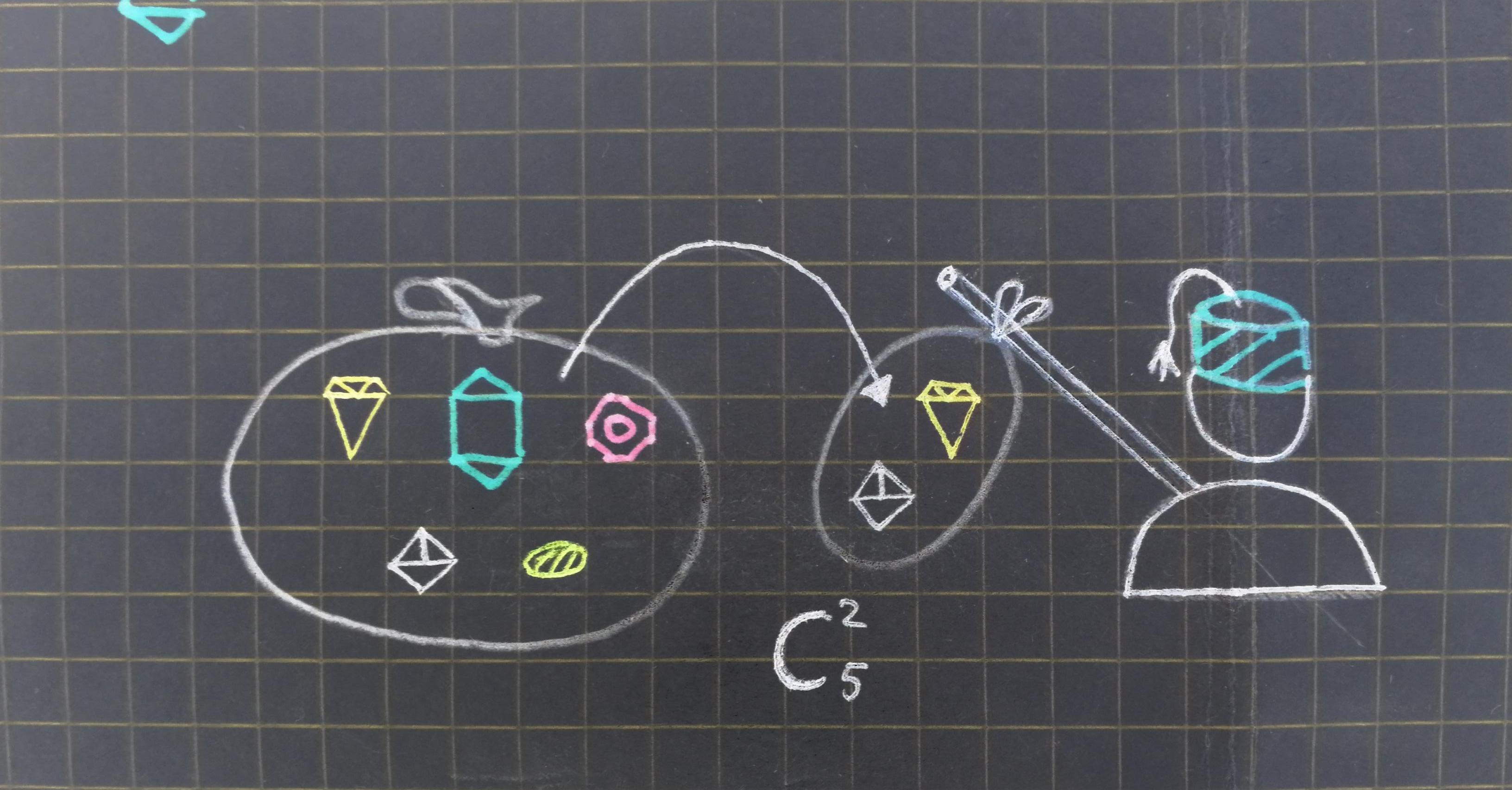
Число сочетаний из n по k с повторениями
Что ж, пожалуй, это самая сложная часть в импровизированном теорминимуме. Эту задачу можно интерпретировать двумя эквивалентными способами. Один будет полезен в статье, а другой поможет вычислить количество сочетаний с повторениями.
Первый способ позволит нам легко найти значение величины . Для этого сменим пластинку: поговорим о том, сколькими способами можно разложить натуральное число
в сумму из
целых неотрицательных чисел (возможно, равных 0). Также будем считать, что порядок при суммировании имеет значение (от перемены мест слагаемых сумма не меняется, но вот наше разложение будет меняться). То есть, хоть 1+2+3 = 2+1+3, для нас это будут разные случаи. Для нахождения числа таких разложений провернем следующий трюк: запишем число
в виде суммы из
единиц. Разбросаем эти единички последовательно по
слагаемым: первые
единиц — это число
, вторые
- число
и так далее вплоть до
. Легко видеть, что
, а это и есть нужное нам упорядоченное разложение! Теперь не составит труда найти их число. Введем для этого в игру
разделитель: они будут отделять одно число в разложении числа
от другого (их
, а не
ровно потому же, почему для разрезания ленты на
частей нужен
разрез). Легким движением мы свели задачу к размещению с повторениями из
по 2 типам:
единиц и
разделитель. А это
. Таким образом,
.
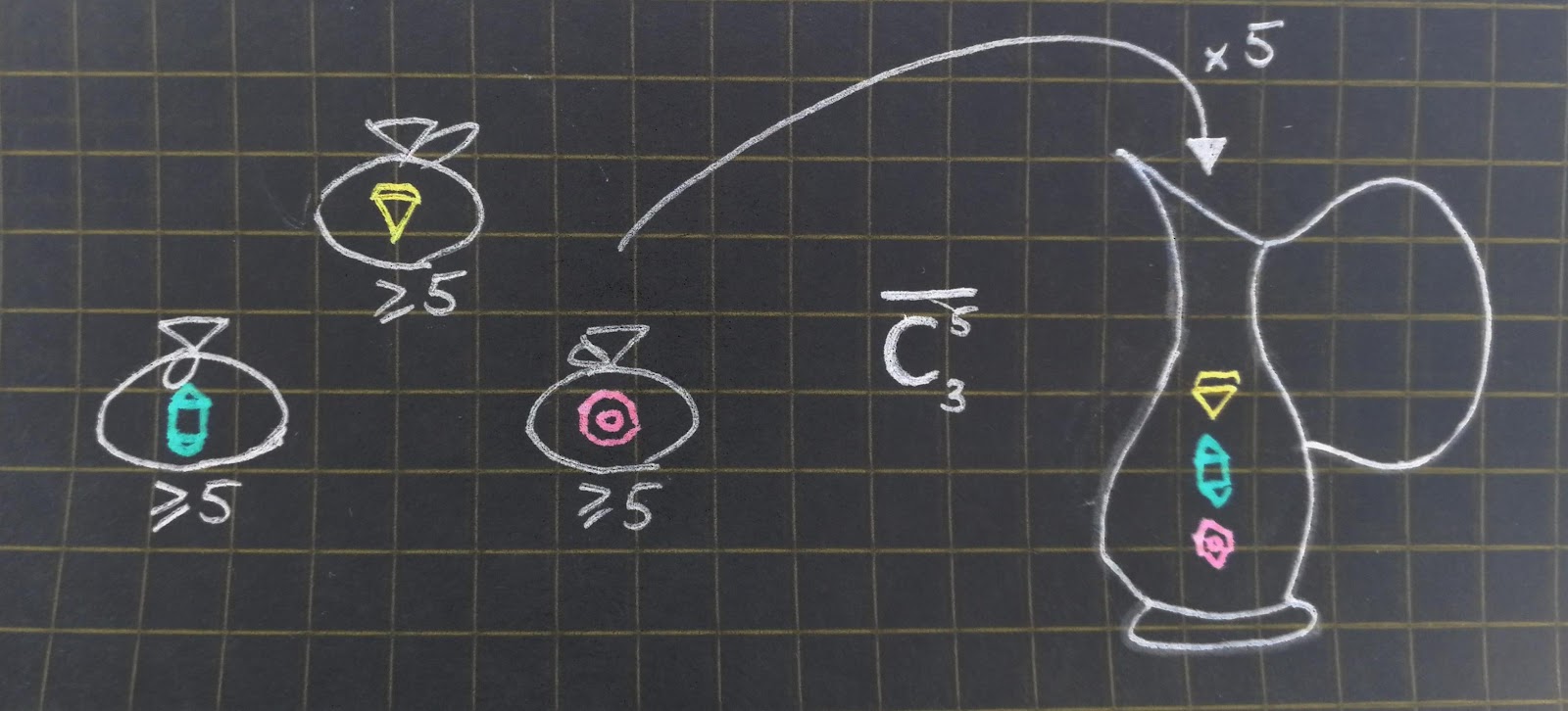
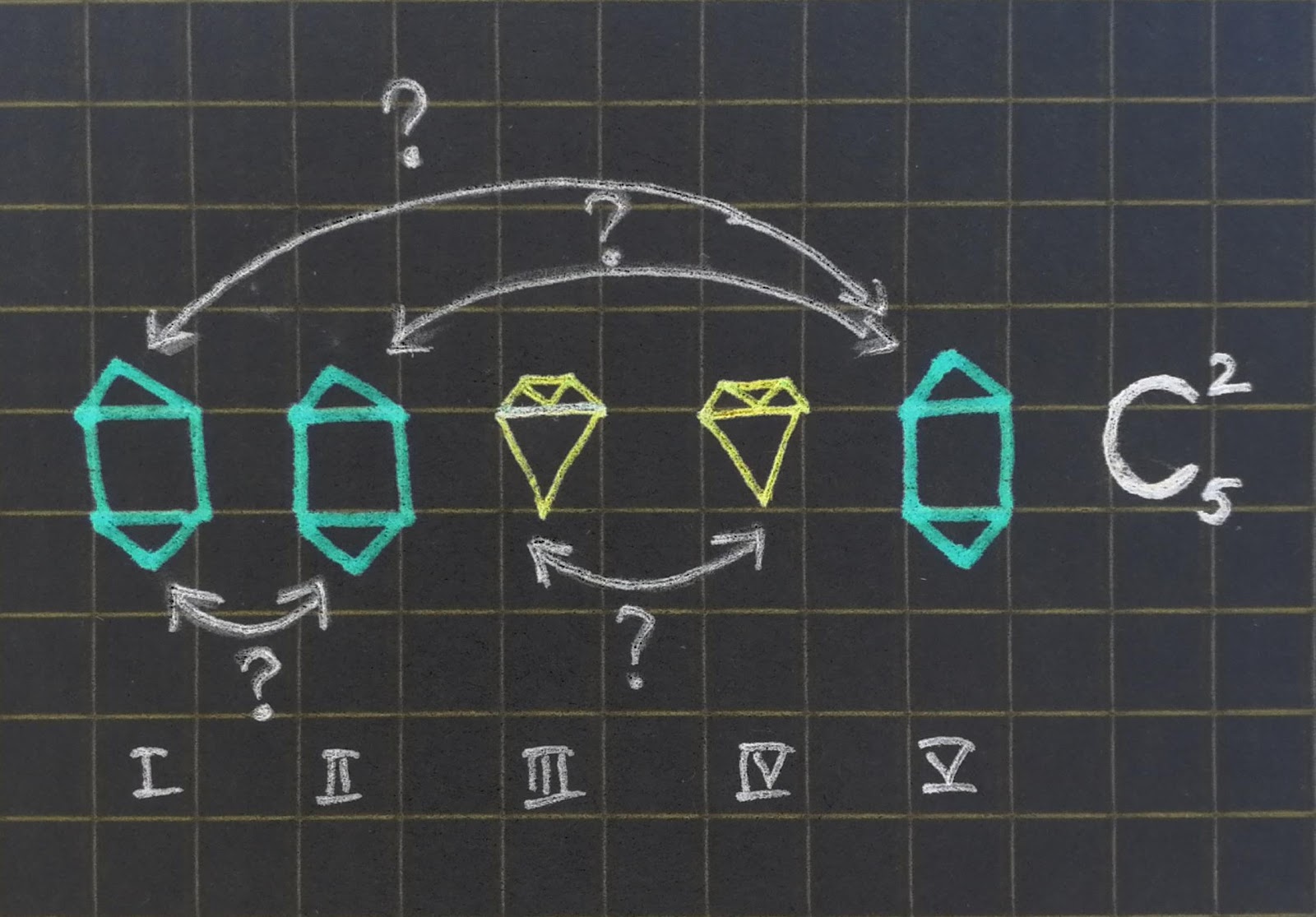
Второй способ, более нам интересный: пусть у нас есть различных типов элементов, элементы одного типа неотличимы друг от друга. Зададимся вопросом: сколькими способами можно выбрать неупорядоченный набор из
элементов, считая, что имеется достаточное количество элементов каждого из
типов (хотя бы по
штук). Тогда представим, что число единиц от левого конца строки до первого разделителя — это число элементов первого типа, число единиц от первого разделителя до второго - второго типа и так далее, наконец, число единиц от последнего,
-ого разделителя до правого конца строки (до конца суммы) - это число элементов
-ого типа. Если какой-либо из типов не попал в набор, то два соответствующих разделителя идут подряд, то есть между ним ноль единиц. Получили эквивалентный результат.
Вероятность (рекомендуется к ознакомлению, если читатель не помнит определения или не знаком с темой )
Теория вероятностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Это один из самых молодых разделов математики, который получил свое строгое обоснование лишь в конце двадцатых годов прошлого века, в работах А.Н. Колмогорова. В наши дни теория вероятностей имеет одно из центральных мест во многих естественных и прикладных науках, начиная от социологии и лингвистики, заканчивая информатикой и квантовой механикой. «Нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы» (Вентцель Е. С.).
Теория вероятностей была известна еще в средние века, но не была оформлена как раздел математики, являясь более набором эмпирических фактов, которые часто формулировались в наглядных представлениях и задачах. В те стародавние времена двигателем прогресса в данном направлении были азартные игры.
В статье нам не понадобится ничего более, чем элементарные факты из теории вероятности, еще «доколмогоровской», скорее «средневеково-азартной», если позволите. Пусть какой-то «черный ящик» (рулетка) выдает случайное «нечто», только одно за раз . Назовем это экспериментом. Пусть число всевозможных «нечто», которые выдает рулетка, равно . Предположим, что все конкретные реализации этого «нечто» появляются одинаково часто (как орел и решка при подбрасывании монеты или как выпадение числа очков от 1 до 6 при бросании кости). Назовем такие реализации элементарными исходами. В таком случае определим вероятность некоторого интересующего нас набора из
конкретных реализаций (назовем набор событием, пусть будет носить имя
) как:
Для экспериментов, где конечно (поставим такое условие, оно будет достаточным), оказывается, что
имеет простую, частотную интерпретацию: это доля элементарных исходов из
в общем числе возможных исходов, когда число повторений эксперимента очень велико. Из определения элементарных исходов ясно, что вероятность каждого из них равна
Введем понятие независимости. Это центральное понятие в теории вероятностей, которое в первую очередь отделило ее от смежных разделов математики. Пусть у нас есть другое событие и
(элементарные исходы лежат и в
, и в
). Они независимы, если вероятность события
равна произведению вероятностей
и
, то есть
. Если событий больше, чем 2 (пусть их
), то надо проверить уже вероятности всевозможных цепочек происходящих одновременно событий (длиной от 2 до
) на то, что вероятность их одновременного появления равно произведению вероятностей каждого события по отдельности. То есть все наборы из 2 событий, из 3 событий … из
событий, происходящих одновременно. Важно, что недостаточно лишь попарной проверки.
Упражнение (со звездочкой): докажите, что число цепочек одновременных событий, необходимых для проверки независимости r событий (об этом написано выше), равно .
Однако для нас интересен самый легкий случай: конечный набор элементарных исходов. Для таких экспериментов независимость можно проверить до безобразия простым образом: важно, чтобы один элементарный исход принадлежал не более, чем одному событию. Можно проверить, что в этом случае определение эквивалентно данному выше.
Назовем события несовместными, если они не могут происходить одновременно (Не пересекаются по элементарным исходам).
Если события несовместны, то вероятность события равняется:
Скажем также про условную вероятность. Условная вероятность события при условии
(иными словами, какова вероятность события
при условии, что произошло
) вычисляется по формуле:
В этой формуле есть небольшая проблема: если событие имеет вероятность ноль, то у нас образуется ноль в знаменателе. Тогда примем, что условная вероятность в этом случае равна нулю, что выглядит естественно.
Осталось вспомнить формулу полной вероятности. Представим, что всевозможные элементарные исходы разбиваются на непересекающиеся события ("разбиваются" - в том смысле, что каждый элементарный исход лежит в каком-то из событий). Мы знаем все
. Пусть нам известны все условные вероятности
. Тогда вероятность события
можно найти по формуле:
Для пояснения последней формулы стоит привести пример. Будем кидать игральный кубик (кубик честный, то есть выпадение каждой грани равновероятно и равно 1/6). Вероятность выпадения четного числа очков равна 1/2. Такая же вероятность и у нечетного числа очков на кубике. Два этих события — разбиение всех элементарных исходов 1-6. Вероятность выпадения числа, кратного 3, при условии выпадения четного числа очков — это 1/3 (только 6 из 2, 4, 6). Вероятность выпадения числа, кратного 3, при условии нечетного числа очков — это тоже 1/3 (только 3 из 1, 3, 5). Тогда вероятность выпадения кратного 3 числа очков на кубике равна: 1/2 * 1/3 + 1/2 * 1/3 = 1/3. Это так, ведь нам интересны числа 3 и 6 среди 1, 2, 3, 4, 5, 6.
Сделаю финальное замечание. Вероятность события — это вещественное число из отрезка от 0 до 1. В литературе, особенно математической, не принято записывать вероятность в процентах (можете назвать это снобизмом). Но для удобства изложения и краткости формулировок часто прибегают к использованию ‘%’, особенно в прикладных областях. Так что и здесь иногда будут использоваться проценты, за что перед особо впечатлительными я заранее извиняюсь.
На мой взгляд, это все, что было бы неплохо вспомнить из комбинаторики и теорвера перед основным текстом. Прошу прощения, если был излишне многословен.
2. Общие слова о pps
Вопрос обеспечения безопасности и эффективности процесса аутентификации пользователя на онлайн-ресурсе — крайне важная задача для компаний и организаций по всему миру, в эпоху бурного развития цифровых услуг, которая получила новый толчок к росту в последние полтора года, в период пандемии.
Существует множество различных методов аутентификации, такие как криптографические токены, биометрия и другие. Однако введение пароля остается наиболее общеупотребительной схемой аутентификации из-за своей простоты, эффективности и надежности (по крайней мере, теоретической). Однако же эта теоретическая, математическая надежность имеет множество «но», связанных с конкретными техническими реализациями процесса аутентификации, работой с реальным оборудованием, с реальным ПО и по реальным каналам связи, где могут возникнуть дополнительные уязвимости, снижающие безопасность системы. Конечно же, одной из центральных причин уязвимости схемы с паролями является человеческий фактор.
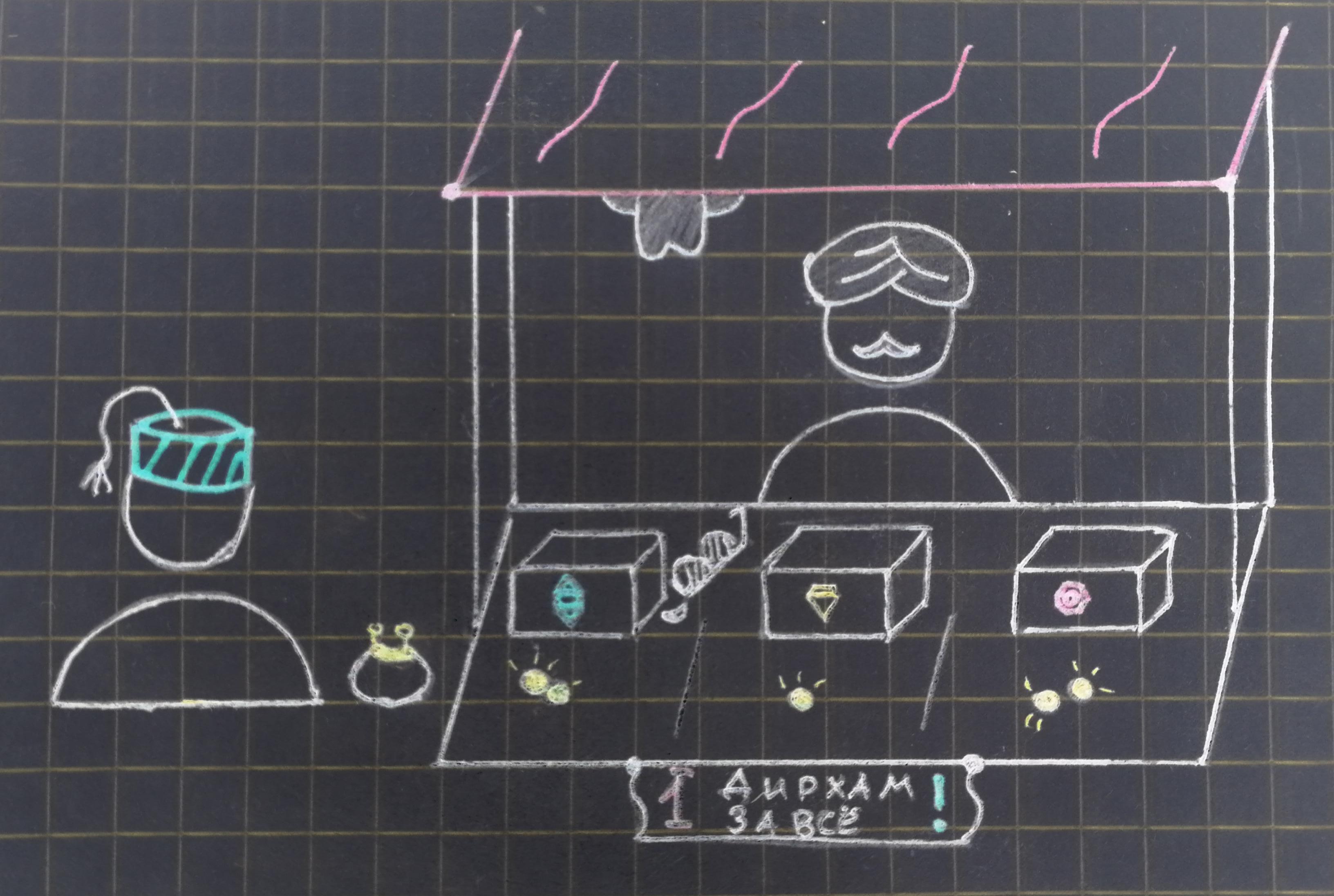
Теоретическая надежность паролей строится на его сложности, а точнее на его достаточной длине, достаточно большом алфавите и независимости, случайности символов в нем. Это делает пароль более защищенным перед различными атаками, связанными со статистическим анализом языка, подбором наиболее употребительных паролей или его частей из утекших баз данных и тому подобных. В идеальной ситуации, пользователю бы следовало выбирать пароль максимальной длины с независимым друг от друга выбором символов из всего доступного алфавита. Само собой, это идет в категорический разрез с человеческой натурой, поэтому, перебрав с десяток паролей-мемов (по типу password, qwerty и т.п.), дат и строк из песен можно взломать множество аккаунтов, что подтверждают многочисленные утечки, одна из которых будет использована в статье.
«We are humans. And sometimes, very humans»
Кроме того, возможны атаки с использованием вредоносных программ, различных кейлоггеров или же атаки с использованием социальной инженерии, как в офлайне (подсматривание пароля, кража имущества с данными об аккаунте), так и в онлайне (вымогательство, введение в заблуждение). Таким образом, злоумышленник может получить данные об аккаунте в один шаг. Также интересным применением может быть работа пользователя в системе, в безопасности которой он не может быть уверен наверняка (например, терминалы или кассы на улице, банкоматы с зловредными скиммерами).

В связи с этим изучаются специальные способы идентификации, с помощью которых можно было бы избежать компрометирования пароля пользователя за один раз. Одно из направлений — использование различных запросов при входе в аккаунт, не требующие ввода пароля целиком [1], [2]. В частности, могут использоваться частичные пароли (partial passwords, pps): сервер запрашивает ввести некоторый случайный набор символов из пароля, указанный при регистрации. Использование pps - простой и эффективный способ противостоять некоторым типам атак, которые могут получить информацию о полном пароле. Утверждается, что такая схема более безопасна, ведь число возможных запросов растет быстро при правильном выборе параметров (об этом более подробно будет написано ниже). Так, для пароля длины n при запросе m символов получаем вариантов запросов в случае, когда позиции не повторяются и
, если допускается несколько одинаковых позиций в запросе.
Кроме того, запрос частичного пароля в виде раздельных окошек с вынесенным отдельно запросом может стать непреодолимой преградой для простых, распространенных вредоносных программ, что делает идею взлома таких аккаунтов более технически сложной задачей.
Частичные пароли широко используются в банковском секторе, особенно в Великобритании (например: AIB, Standard Life, Barclays, HSBC, Bank of Ireland и др.), как часть двухэтапного (как минимум) процесса аутентификации [1]. Такое доверие к технологии, которая мало обсуждалась в научном сообществе и слабо изучена, может удивлять, как и ее широкое распространение лишь в нескольких странах в мире.
Поговорим об основных типах атак на pps. В большинстве своем, атаки на обычные и частичные пароли совпадают, за тем исключением, что злоумышленнику, как правило, требуется несколько перехватов информации о пароле, чтобы с большой вероятностью успешно ответить на очередной запрос сервера. Приведем основные типы атак:
Bruteforce: злоумышленник перебирает все возможные комбинации паролей в доступном алфавите. Далее он перебирает их по очереди, пока ответ на очередной запрос не будет успешным.
Атака с использованием словаря: при атаке используются статистические методы, основанные на частоте встречи букв в языке, на характерных сочетаниях букв и слов, распространенных видах паролей из скомпрометированных баз данных и т.п.
Кейлоггер (атаки с запоминанием): злоумышленник использует программу, чтобы отслеживать нажатия клавиш пользователем и использует накопленные данные для взлома всего пароля.
Разумеется, более эффективными являются комбинации описанных выше методов атак. Отдельно будет рассмотрена уязвимость pps, связанная с атакой не на конкретного пользователя, а на большую группу аккаунтов (trawling attack).
Вредные советы (перед прочтением сжечь)
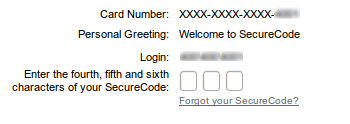
Для желающих, в качестве теста, я ни при каких обстоятельствах не стал бы оставлять ссылку на сайт английского банка. На нем не советовал бы, введя случайные символы в качестве имени, увидеть пример интерфейса ввода частичного пароля (здесь – securecode, как дополнение к основному паролю). Now remember, I told you nothing, okay?
3. Детали реализации pps
Поговорим о том, как работают pps более подробно. Частичный пароль — это запрос ввода части символов из полного пароля. Протокол состоит из следующих этапов [2]:
Регистрация: пользователь выбирает пароль
длины
, состоящий из символов некоторого алфавита (например, цифры для PIN, цифры и буквы для буквенного пароля). Выбор в некотором формате сохраняется на сервере (об этом будет рассказано в чуть ниже).
-
Вход в систему: процесс аутентификации представляет собой последовательность вопрос-ответ:
Вопрос: сервер выбирает некоторое подмножество натуральных чисел
из
и отправляет запрос ввода
пользователю
Ответ: пользователь отвечает на запрос в форме
. Вход в систему производится только в случае
для всех
(то есть если предоставленные данные корректны).
Позиция |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Пароль |
s |
e |
s |
a |
m |
e |
o |
p |
e |
n |
Запрос (2,3,6) |
e |
s |
e |
Остается простор для выбора оптимальных параметров: какой размер пароля стоит выбрать? Какое число
символов стоит запрашивать? Какое число попыток предоставлять пользователю? Допускать ли в запросе одинаковые позиции? Изменять ли запрос при неудаче и как часто? Попытаемся ответить на эти вопросы.
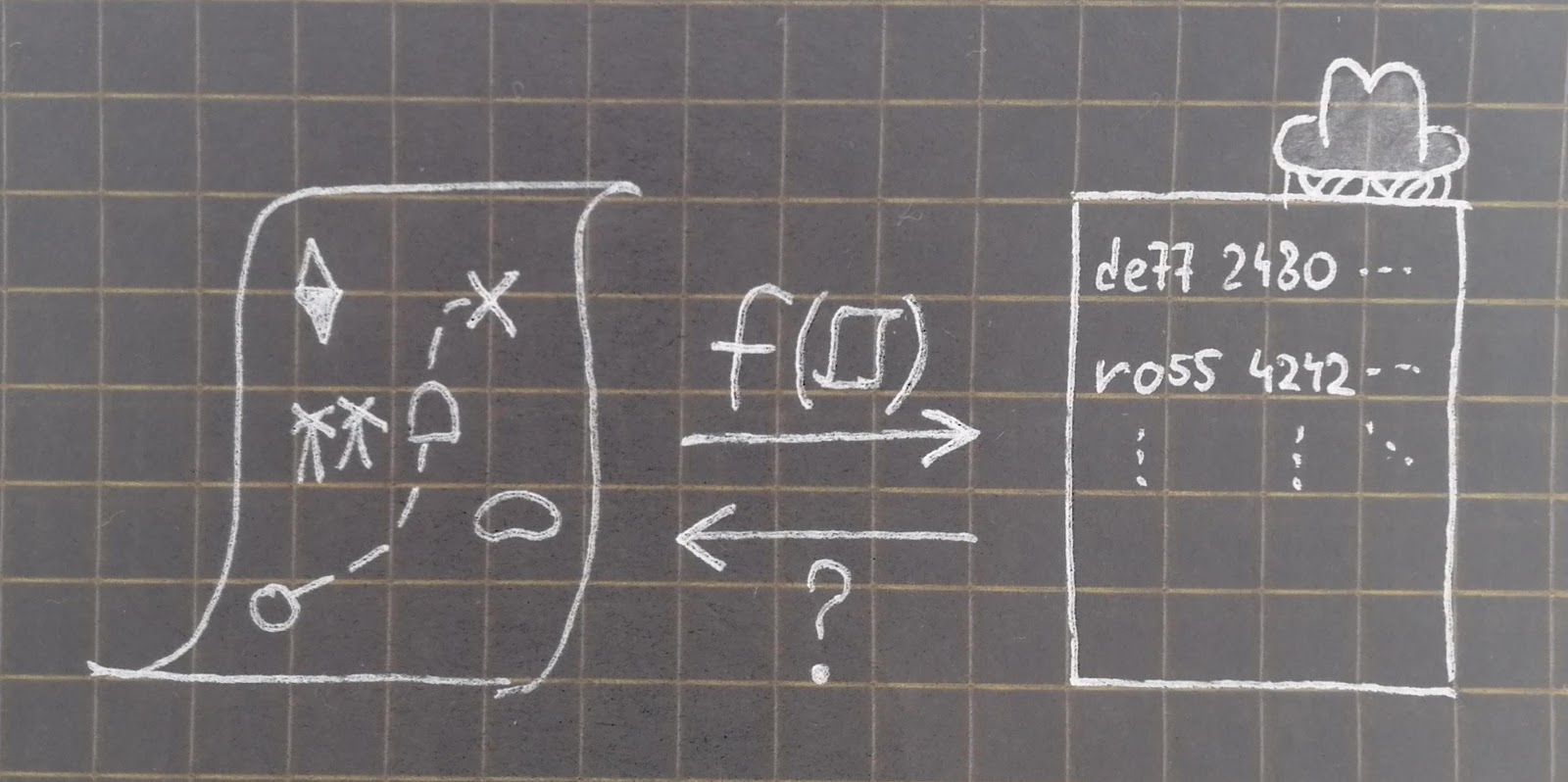
Интерес вызывает то, каким образом стоит хранить пароли пользователей на стороне сервера. Как правило, в классических реализациях аутентификации с помощью пароля на стороне сервера достаточно хранить только хэш от пароля (еще почитать можно тут). В этом случае нахождение пароля по данному значению хеша (или другого пароля с таким же значением хэша) является вычислительно сложной задачей, допускающей только полный перебор (впрочем, и тут есть некоторые уязвимости). Так что злоумышленник или нерадивый администратор, даже получив базу данных паролей с сервера, не сможет восстановить пароли по записанным там значениям хешей. В этом смысле такой подход значительно лучше, чем хранения пароля в виде текста. К примеру, широко распространены хеш функции семейства SHA (https://ru.wikipedia.org/wiki/SHA-2).
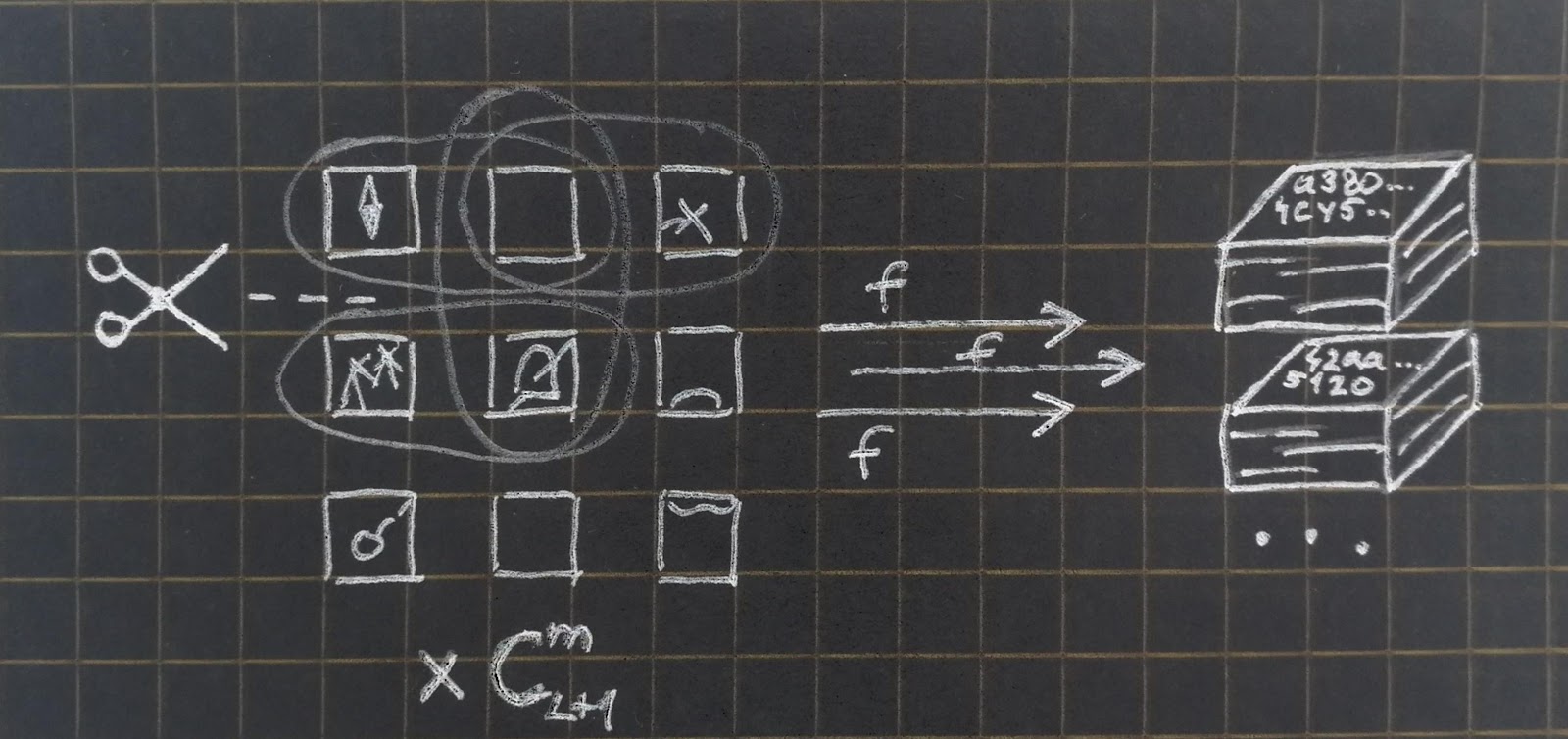
Однако в случае использования pps возникают некоторые сложности. Если вернуться к идее использования хешей, то нам придется хранить все возможные значения хеш-функции при выборе m из символов пароля. Так, при выборе позиций без повторений получаем
комбинаций. Например, для
— символьного пароля и запроса длины
получаем
значений, которые необходимо запомнить серверу. Для SHA-256 получаем 256 бит * 120 = 3.75КБ. Довольно много в сравнении с 1 хешем в классической схеме.
Можно здесь сделать также интересное замечание: возможно, подбор параметров pps многими банками как раз был связан с использованием всего множества значений хешей. Как правило, у них равно 2-3, а длина пароля
довольно сильно ограничена, что сильно бьет по безопасности использования pps.
Что ж, не вернуться ли к идее хранения паролей в виде текста? На секунду может прийти такая мысль. От нее сразу же лучше отказаться: велика опасность компрометирования паролей пользователей. Это не вариант.

Другая возможная реализация заключается в следующем: пароль может храниться на сервере в зашифрованном виде с использованием какой-либо схемы симметричного шифрования, например AES. Тогда управление ключами может осуществляться с помощью оборудования, защищенного от несанкционированного доступа, например аппаратного модуля безопасности (Hardware security module, HSM) или отдельного сервера аутентификации с системами контроля доступа, чтобы избежать несанкционированного получения третьими лицами криптографического ключа. Так мы получаем черный ящик для шифрования и проверки подстрок символов в пароле, а именно: введенные символы пароля передаются в приложение, далее на HSM или сервер аутентификации вместе с паролем в зашифрованном виде. Далее HSM может расшифровать пароль и подтвердить или опровергнуть правильность предоставленных пользователем символов. Недостатком этого метода является использование специального оборудования и серверов, что увеличивает накладные расходы. Кроме того, в процессе аутентификации все же происходит полная расшифровка пароля, и при определенных обстоятельствах, может произойти утечка всего пароля.
Схема разделения секрета
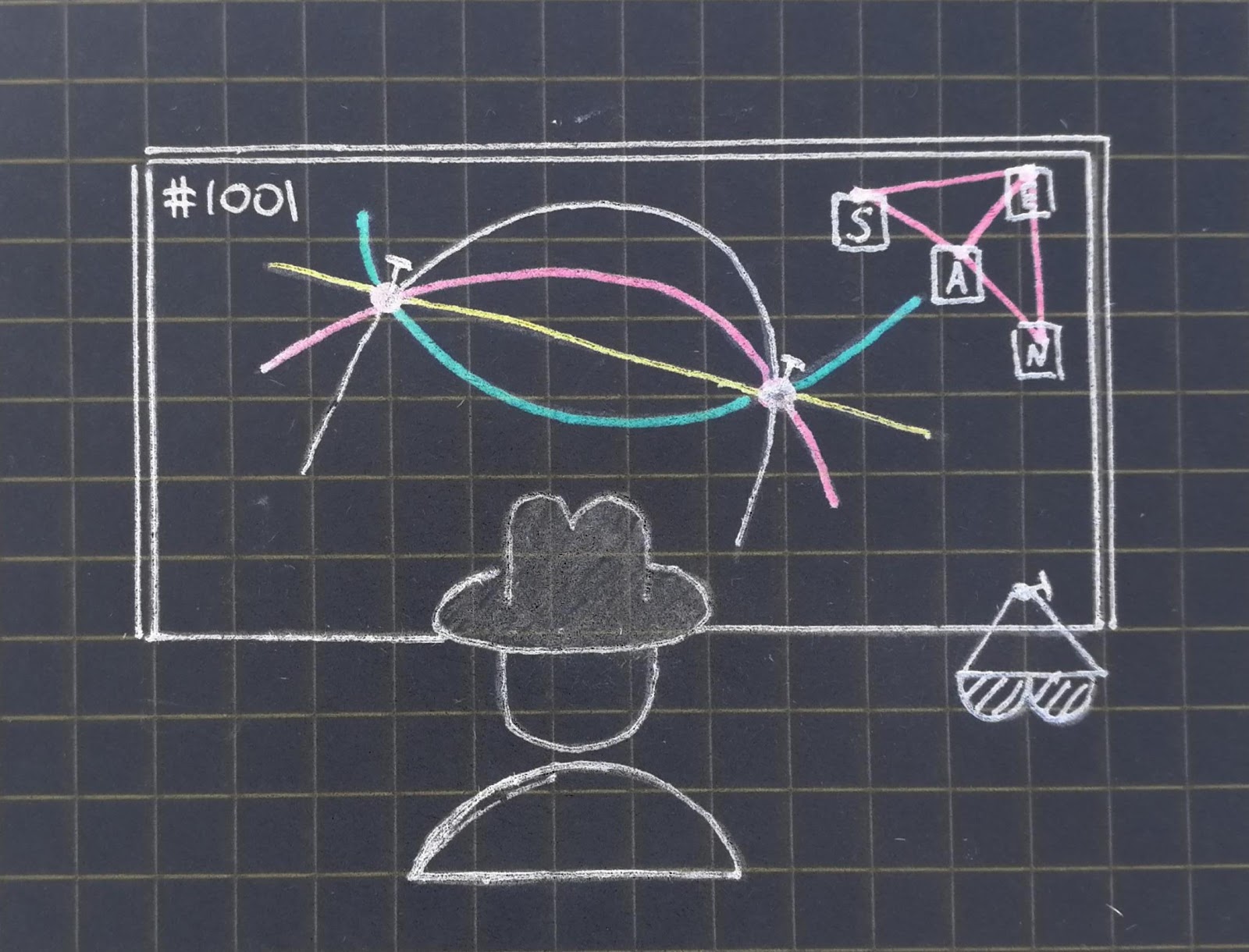
Наиболее естественной реализацией является использование схем разделения секрета (например, схема Шамира). Схема Шамира позволяет реализовать — пороговое разделение секрета между
сторонами таким образом, чтобы только любые
или более сторон могли восстановить секрет. При этом,
и менее сторон не могут получить никакой информации о секрете. В контексте pps секретом является пароль (точнее, хэш от пароля),
— число символов в пароле, а
— число символов в запросе. Как раз такая схема будет использоваться в модельном примере в конце статьи.
Обсудим идею схемы Шамира. Она довольно проста: для того, чтобы однозначно интерполировать многочлен степени требуется не менее
точек. Так, для восстановления прямой нужно хотя бы 2 точки, а для параболы — хотя бы 3. Оказывается, что при меньшем числе точек однозначная интерполяция принципиально невозможна. Если нам требуется разделить секрет между
людьми так, чтобы восстановить его могли только любые
или более человек, то мы используем его в качестве слагаемого в многочлене
степени. Восстановить же многочлен можно при наличии минимум
точек. На практике используются не вещественные числа, а конечные поля (удобны для использования в оборудовании), так что, в отличие от непрерывного случая, число различных точек многочлена ограничивается размером конечного поля (а оно выбирается очень большим).
4. Виды атак на pps
Bruteforce
Обычная bruteforce-атака использует лишь информацию об алфавите (алфавит можно узнать при регистрации). Пусть размер алфавита равен . Предполагая, что символы пароля распределены равномерно (смелое предположение), вероятность полностью отгадать наугад выбранный пароль равна
. Так, для шестизначного PIN (пароль из цифр) это будет
, а для десятизначного пароля из латинских букв и цифр (будем называть его для краткости просто пароль) вероятность будет порядка
. Вероятность отгадать частичный пароль равна
. Для PIN при
это пугающие
, а для пароля при
это около
. Такие параметры паролей были выбраны, так как они наиболее распространены в реальных системах [1].
Скажем, что при регистрации пользователю предоставляется попыток ввода частичного пароля. При превышении этого числа налагаются какие-либо санкции (временная или постоянная блокировка аккаунта). Понятно, что в случае неизменного запроса вероятности угадывания увеличиваются в
раз (до
), что еще сильнее упрощает взлом пароля. Это открывает просторы для так называемых trawling attacks (переведем как ковровый взлом), когда осуществляется попытка взлома не конкретного аккаунта, а большого набора аккаунтов с целью украсть некоторую их долю.
Между делом, хочу еще раз напомнить, что pps часто используются в комплексе с другими средствами безопасности, такими как: запрос дополнительных данных о пользователе, двухфакторная аутентификация (почта, сообщения) и другими.
Само собой, атаки с полным перебором — это самый примитивный вариант для взлома. Однако если бы все пользователи выбирали пароли со случайным набором символов, то ничего лучше предложить злоумышленнику в этом случае и не получилось. Но люди используют некоторые устойчивые конструкции языка, слова, благозвучные комбинации букв, даты и тому подобное. Поэтому можно придумать что-то получше. Чуть более сложный вариант взлома паролей — использование данных о частоте встречи букв на определенных позициях. Так и назовем следующих подраздел.
Атака с использованием данных о частоте появления отдельных символов на определенных позициях

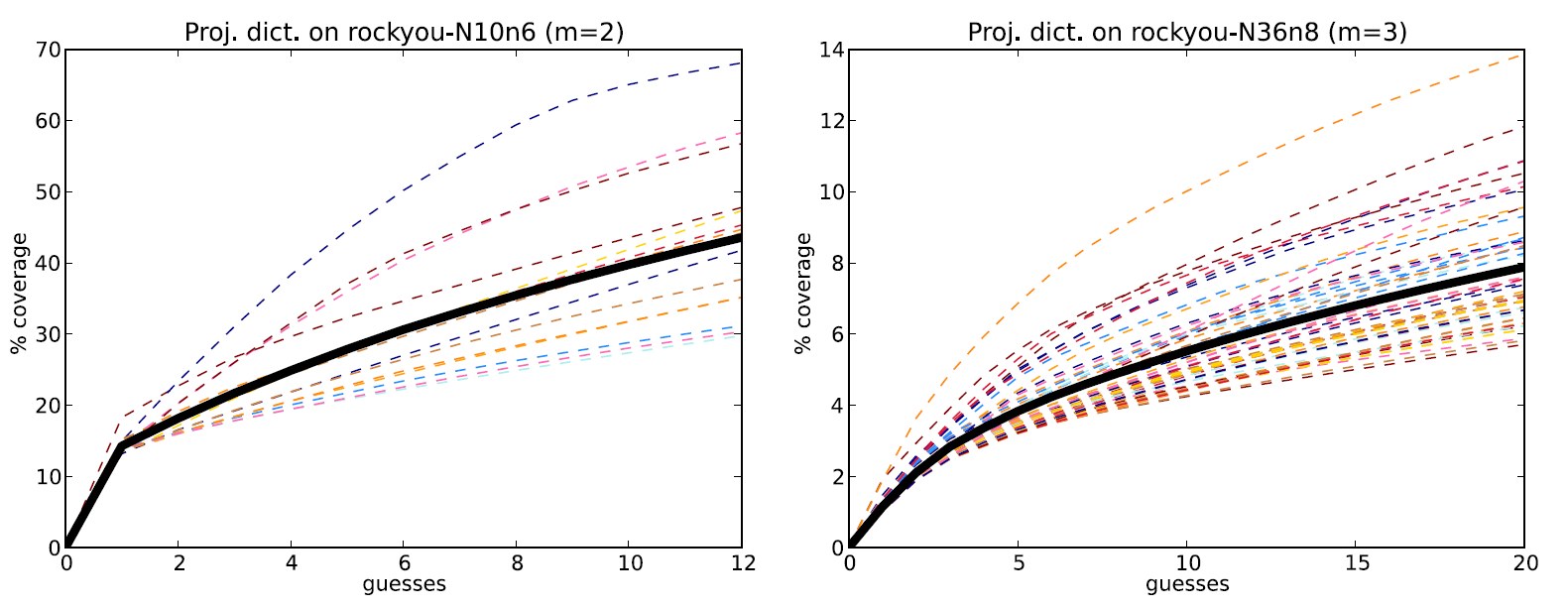
Теперь будем не просто случайно подбирать символы на каждую позицию, а использовать то, насколько часто тот или иной символ встречается в языке или, что еще лучше, в паролях, украденные базы с которыми были выложены в общий доступ. В статье рассматривается утечка базы RockYou, которая произошла в 2009 году. Это 32 миллиона паролей от сайта с приложениями, которые попали в сеть и теперь доступны всем желающим, в том числе и для научных изысканий. Приведем графики, на которых изображена зависимость частоты появления цифр в зависимости от позиции в шестизначных паролях из цифр (алфавит размера , верхний график) и тот же график для паролей из букв и цифр из 8 символов (алфавит размера
, нижний график):
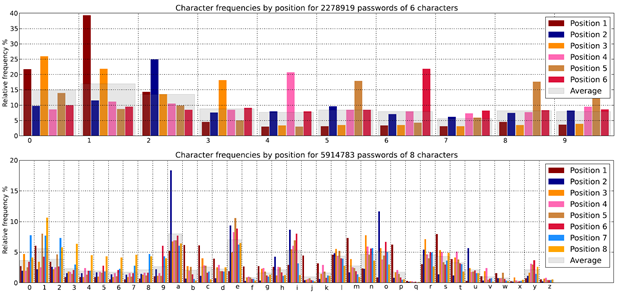
Так, на графике видно, что буква ‘a’ встречается в среднем в 8% случаев в каждой позиции в 8-буквенных паролях, но на 2-ой позиции появляется в 18% случаев. То же и про цифры: так, в 6-значных PIN цифра ‘1’ встречается в 17% случаев в каждой позиции, но в 40% случаев на 1-ой позиции (вероятно, связано с датами и "123456").
Теперь попробуем провести эту атаку на саму же базу, работающую с pps, используя информацию о частоте появления букв в каждой из позиций (пароли будем выбирать случайно). Размеры PIN все те же 6 цифр, запрос цифры; размер пароля равен 8 цифр или букв, запрос
. Графики зависимости вероятности взлома случайно выбранного частичного пароля от числа попыток ввода g приведены ниже (слева — PIN, справа - пароль):
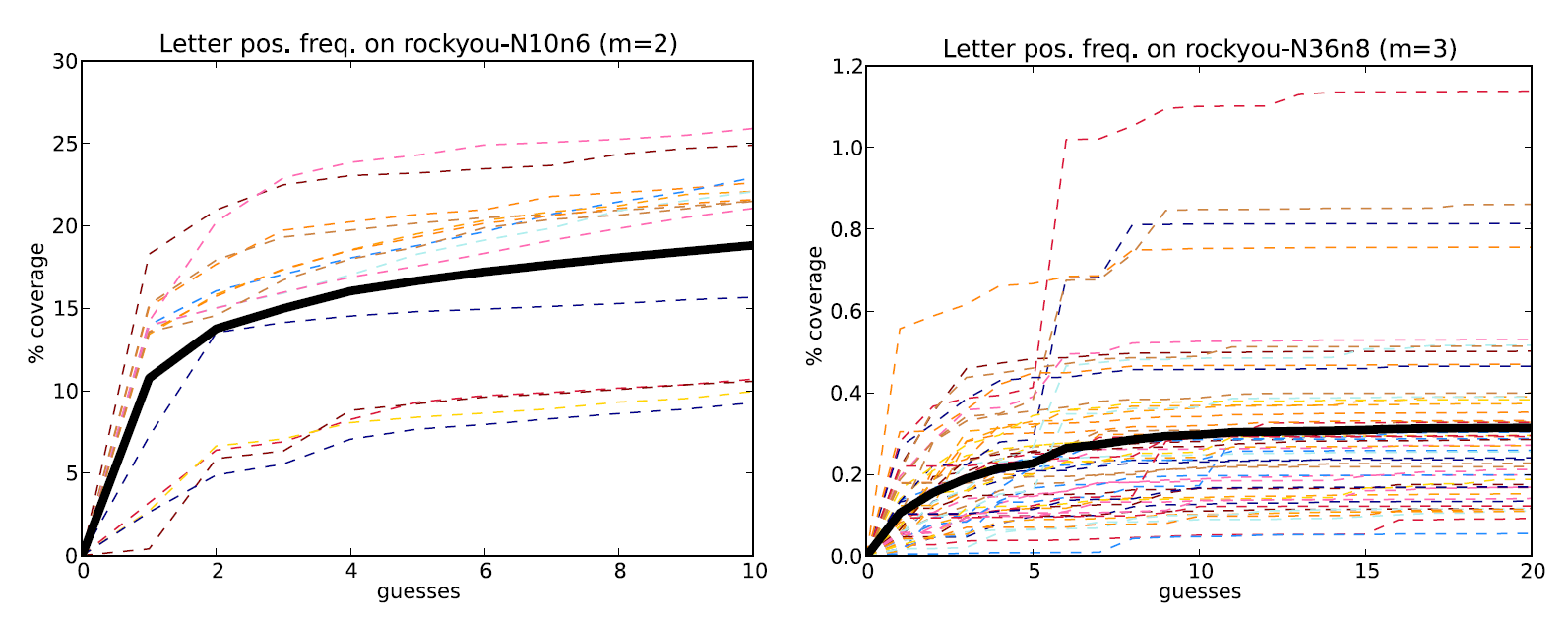
Заметим, что на левом графике 15 линий (ведь есть возможных запроса pps), а на правом — 56 (
запросов). Черная сплошная линия указывает среднюю по типу запроса вероятность правильно ответить на запрос при
доступных попытках. Для PIN получаем вероятность 0.17 (17%) ответить на запрос при 6 попытках, а для пароля имеем вероятность 0.0003 (0.3%) при 10 попытках. Мы можем назвать эти величины вероятностями, ведь мы считаем, что запрашиваемые позиции были распределены равномерно, а аккаунты для взлома выбирались случайным образом.
Уже намного лучшие показатели, но язык не состоит из всевозможных сочетаний букв. Одни сочетания букв встречаются часто (например, «ing» или «con»), другие не встречаются вовсе (к примеру, «aaa» или «ww»). Поговорим далее об использовании сочетаний букв из английского языка для взлома pps.
Атака с использованием данных о частоте сочетаний символов на определенных позициях. Подбор пароля.
Теперь будем использовать данные о частоте встречи сочетаний букв в языке. Так, при запросе частичного пароля, будем принимать во внимание частоту появлений символов одновременно на требуемых позициях.
Было взято 11600 8-буквенных слов английского языка (из словаря ubuntu). Для запроса 2,3,6 позиций оказалось 2736 возможных ответа (16% от возможных) и 1793 для позиций 1,2,3 (10%). Ниже приведена таблица с самыми распространенными сочетаниями символов для соответствующих запросов. Так, для запроса 2,3,6 первые 5 вариантов покрывают 2.87% от общего числа возможных слов, для запроса 1,2,3 получаем 3.74%. При
получаем значения 5.1% и 6.3% соответственно.
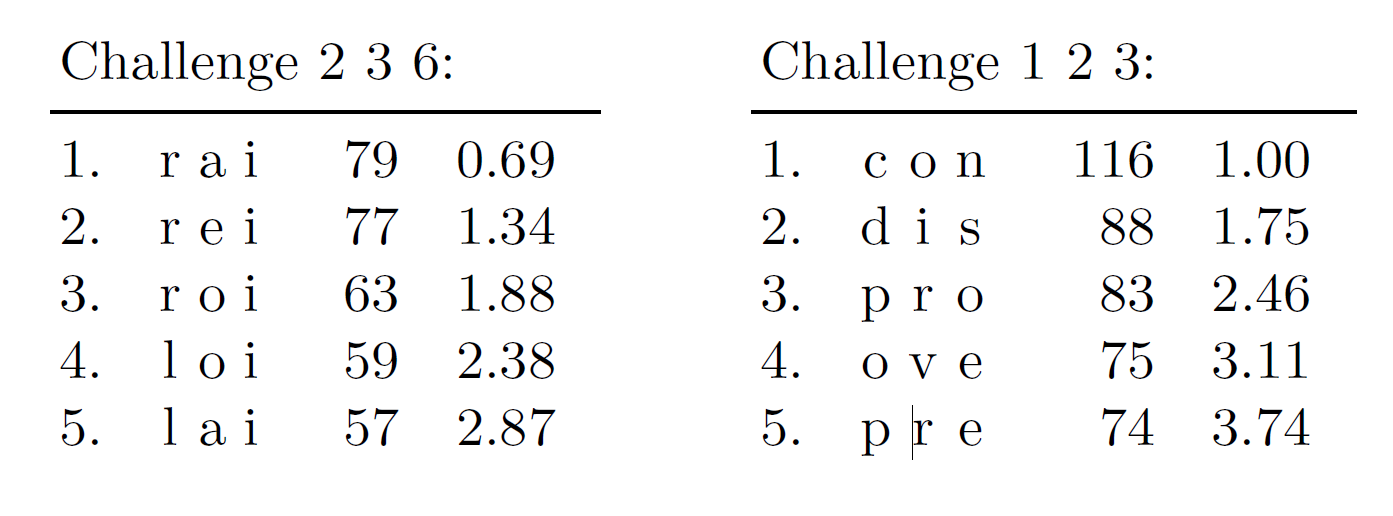
Для запроса 6,7,8 получаем около 30%! Результат оказывается таким большим из-за распространенного окончания «ing». Построим графики зависимости доли взломанных pps для всех возможных запросов и среднее значение доли успехов от числа попыток ввода:
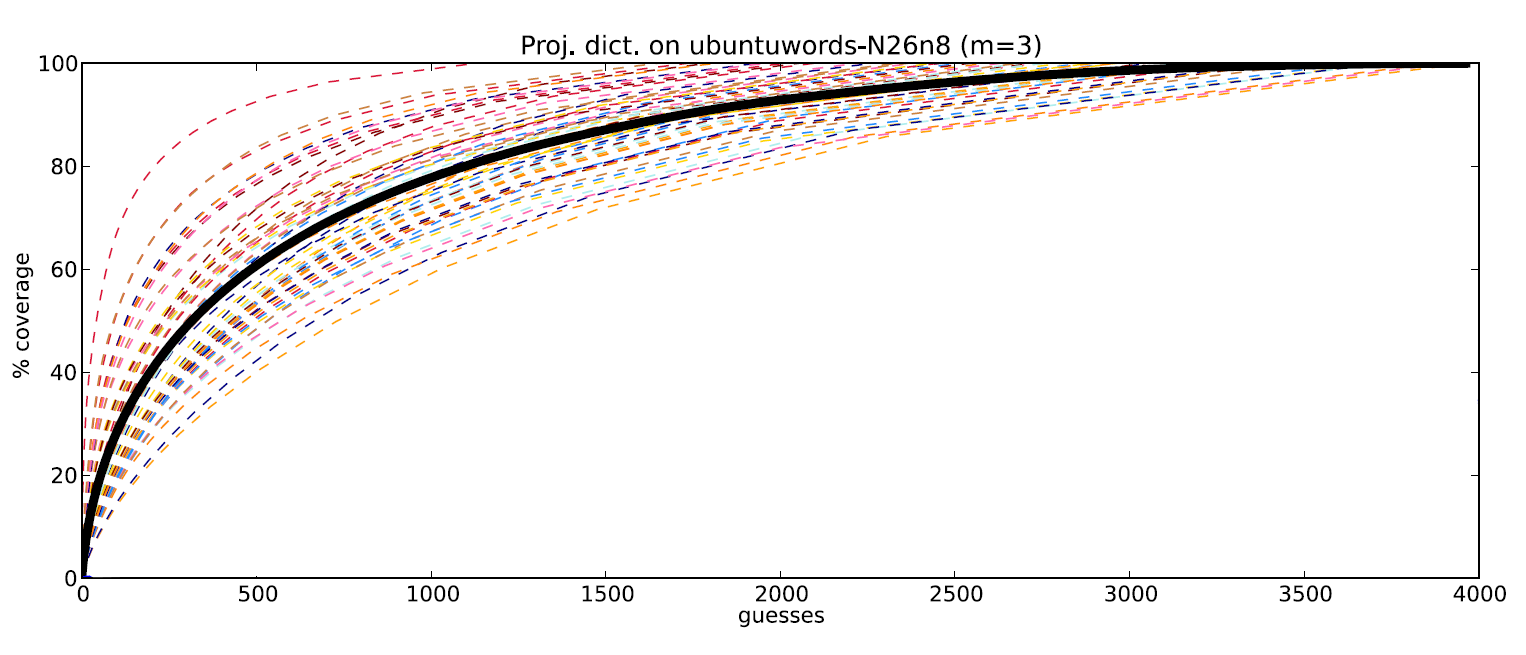
Видим, что для того, чтобы практически в 100% случаев взломать pps требуется порядка попыток. Для случайного подбора символов потребовалось бы до
попыток (в среднем, порядка 8000-9000).
Использовать сочетания букв из словаря — хорошая идея. Но что будет, если учиться на базах данных взломанных паролей?
Атака с использованием данных о частоте сочетаний символов на определенных позициях в реальных паролях

Можно проделать те же рассуждения, но основываясь на утечках из баз данных паролей. Вновь обратимся к базе RockYou. Так, 5 самых популярных 8-символьных паролей покрывают около 3% от всех паролей, что выглядит удручающе. Для PIN первые 6 охватывают 15.3% от общей доли, притом 12.8% (!) приходится на «123456». Хочется надеяться, что пользователи выбирают пароли для аккаунтов в финансовых и государственных учреждениях, соцсетях более осознанно, чем на сайтах игр, но все новые и новые сливы баз паролей, к сожалению, говорят об обратном.
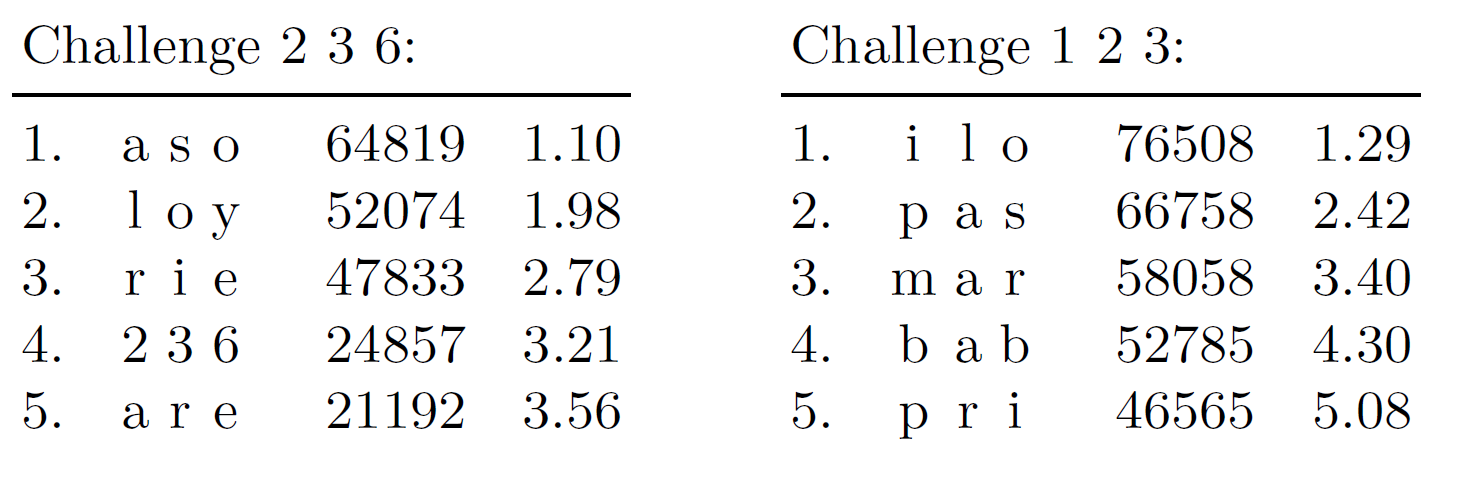
Понятно, что такие проценты взлома пароля на 3-4 порядка превышают обычную bruteforce-атаку. Теперь перейдем к pps и найдем долю самых распространенных сочетаний букв для тех же запросов, что и в предыдущем разделе (см таблицу).
Теперь попытаемся взломать пароли из базы: снова будем брать случайный пароль и случайный запрос, выбирая для каждого типа запроса ответ с вероятностью, пропорциональной частоте встречи сочетаний во всей базе. Графики доли взломанных паролей для PIN (слева) и пароля из букв и цифр (справа) с теми же параметрами от числа попыток имеют следующий вид:
Здесь мы получили наилучший результат атаки: от 22% до 50% со средним 30.6% для PIN с 6 попытками и от 4.2% до 10% со средним 5.5% для пароля из цифр и букв c 10 попытками.
Далее рассмотрим атаки, для противостояния которым и созданы pps: кейлоггинг или атаки с запоминанием.
Кейлоггинг (атаки с запоминанием)
Вот мы и пришли к атаке, с которой, как предполагается, эффективно справляются pps. Рассмотрим этот случай подробнее. Для теоретической оценки оптимальных параметров построим математическую модель частичных паролей.
Пусть пользователь создал пароль длины
с символами
из алфавита
,
. Рассмотрим два сценария:
Сценарий A (без повторений). Запрос вида
, где
для
, при этом
для различных
и
.
Сценарий B (с повторениями). Запрос вида
, где
для
(запрос может содержать повторяющиеся позиции).
Будем считать, что злоумышленнику удается перехватить вид запроса и ответ до того, как эти данные будут зашифрованы. Построим теоретические зависимости вероятности того, что пароль будет восстановлен полностью и вероятности того, что на запрос pps можно будет ответить с достаточно большой вероятностью от числа попыток ввода . Для этого докажем следующую теорему:
Теорема
Пусть — число различных позиций в пароле, которые удалось узнать злоумышленнику после
запросов pps. Тогда вероятность
того, что злоумышленник знает ровно
из
символов пароля, может быть рекуррентно найдена с помощью формул (I) и (II) для сценариев A и B соответственно:
Докажем этот факт. Действительно, если злоумышленник на момент предыдущего, -ого шага, заполучил
различных позиций в пароле и надеется знать ровно
на следующем,
-ом шаге, то в запросе из
символов требуется узнать ровно
из оставшихся неизвестными
символов и «добрать» лишние
.
В сценарии A повторения не допускаются. Очередной, -ый запрос, можно составить
способами (стоит в знаменателе, как общее число элементарных событий). В числителе имеем сумму из
слагаемого (
интересующие нас несовместные события), каждое из слагаемых говорит об одновременном выполнении трех условий:
На
шаге было известно
символов (
);
выбор в запросе недостающих
символов из неизвестных
(сочетания без повторений,
);
выбор в запросе оставшихся
из
уже известных символов (сочетания без повторений,
).
Рекуррентная последовательность начинается с . Вероятность равна нулю, если событие нереализуемо. Можно заметить, что, по факту, каждое слагаемое, с учетом знаменателя и без
, является функцией вероятности гипергеометрического распределения
.
В сценарии B выбираются символов из доступных
, ведь мы допускаем в запросе повторения. Рассуждения остаются теми же с той разницей, что в запросе могут быть повторения в позициях символов. Поэтому общее число возможных запросов равно
и «добор» уже известных символов может быть с повторениями (сочетания с повторениями,
Две основные формулы нами получены. Построим теперь зависимость вероятности от числа запросов
(перехваченных злоумышленником) для нескольких значений размера запроса
и длины пароля
:
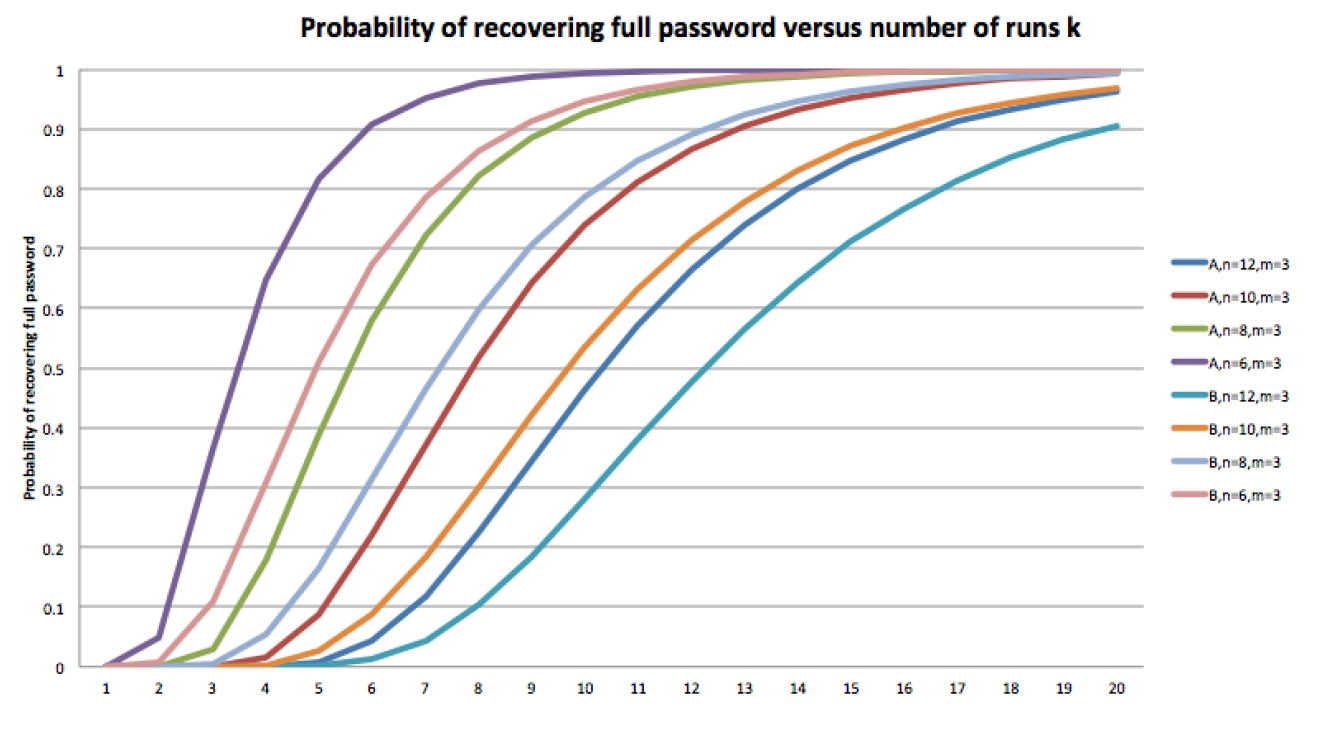
Как мы видим, в сценарии B вероятность полного раскрытия пароля ниже, чем для A при всех значениях числа попыток . Так, для
и
злоумышленник будет знать весь пароль с вероятностью в 0.7 при знании ответов на 7 запросов в сценарии A и при знании 11 запросов в сценарии B. Для
и
для вероятности 0.75 необходимо знание 14 и 17 запросов в сценарии А и B соответственно.
Теперь рассмотрим, с какой вероятностью злоумышленник точно ответит на следующий запрос, имея информацию о запросах и зная
позиций с символами (условная вероятность). Имеем:
После запусков вероятность того, что в очередном запросе будут позиции символов, которые ему уже известны, вычисляется по формуле полной вероятности и равна:
Приведем графики зависимости этих величин для некоторого набора параметров:
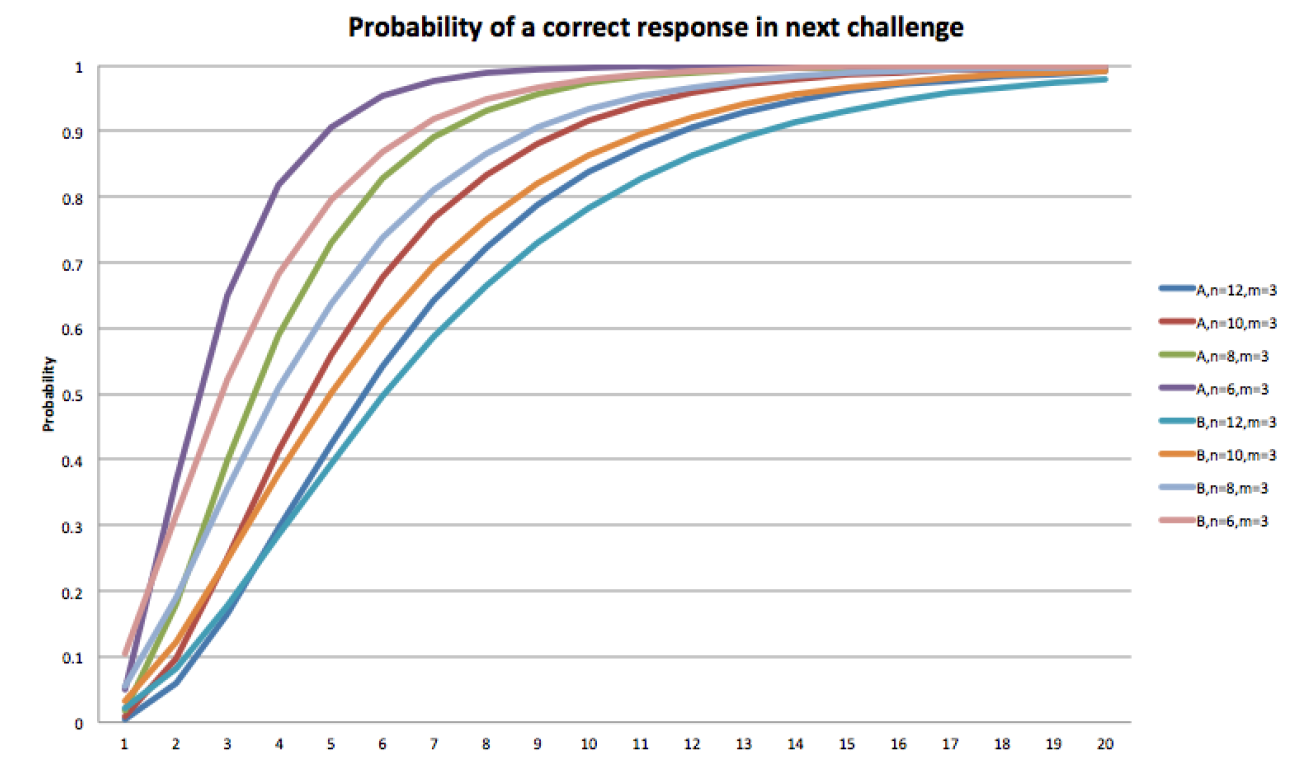
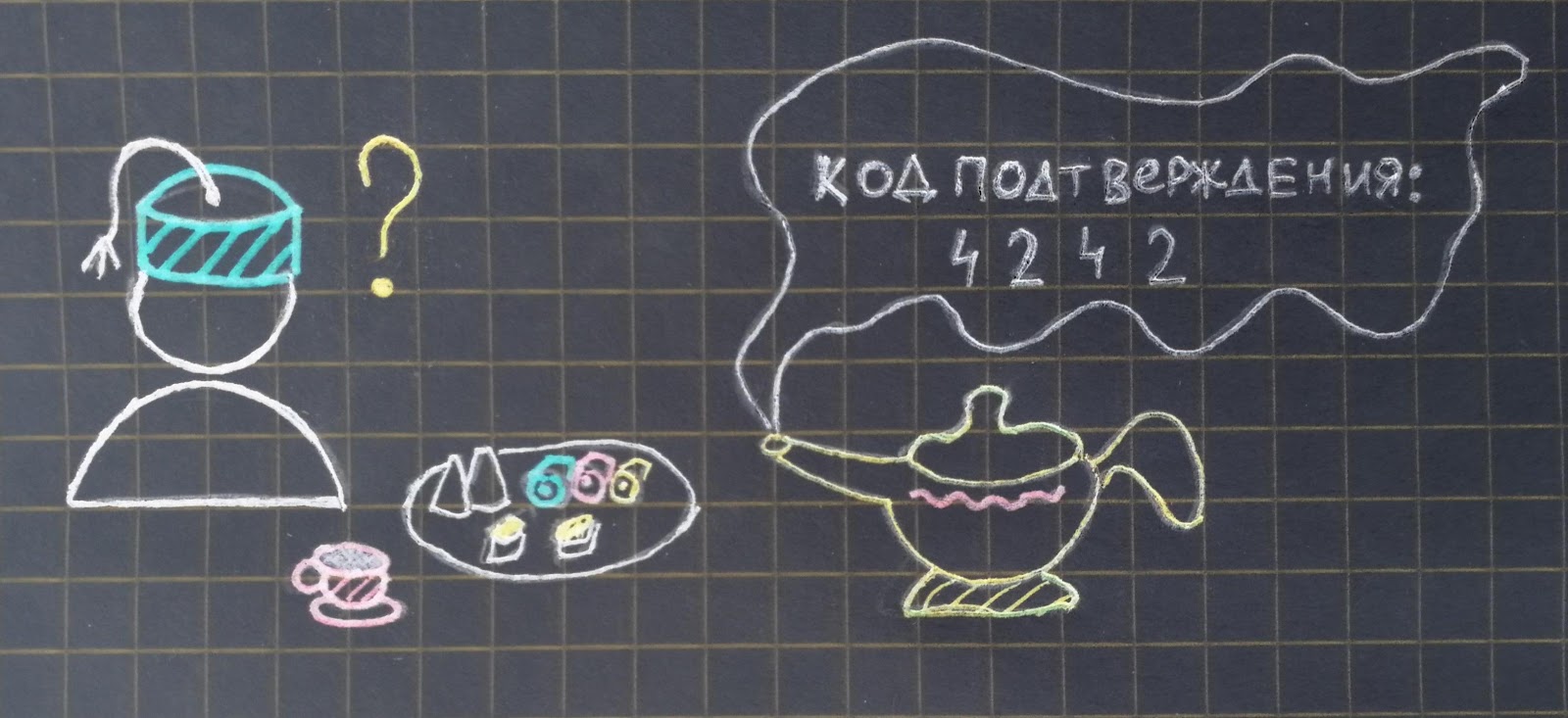
Видим, что хотя на первых нескольких попытках вероятность ответа чуть ниже у сценария A (так как в запросе не может быть повторов), но для всех остальных значений сценарий B имеет значительно более высокую стойкость к взлому. Однако, при выборе параметров, близких к используемым на практике, устойчивость к взлому все равно пугающе низкая (благо это только один из этапов аутентификации). Так, в случае и
имеем вероятность взлома в 0.75 после 8 запросов в сценарии A и после 9 в сценарии B.
Сценарий B показывает лучшие результаты в сравнении со сценарием A (что довольно неожиданно). Но все же, запросы вида «Введите символы 1,1,3» или, тем более, «Ждем позиций 7,7,7» будут выглядеть несколько странно. Напомним, что такие выводы проделаны в сценариях, где злоумышленник пытается взломать пароль наверняка, не занимаясь подбором (крайне актуально в случае, когда он не хочет дать знать своей жертве о своих попытках входа).
Атака, когда позиции символов неизвестны
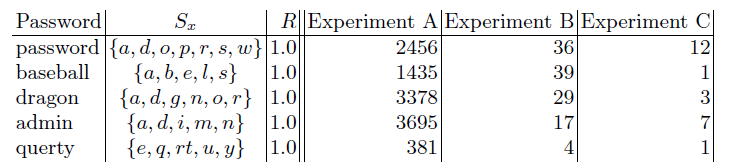
Вкратце поговорим о таком виде атак. Предположим, что по какой-то причине злоумышленнику удалось перехватить некоторое множество символов, но он не знает, на каких позициях они расположены (можно придумать случай, когда кейлоггер уж совсем неизобретательный и не может отследить текст запроса, а только нажатие клавиш). Рассмотрим, для простоты, случай, когда известен весь набор букв в слове (например, кейлоггер работал на компьютере пользователя месяцами и наверняка перехватил все возможные комбинации символов). Для сравнения, рассмотрим случай, когда известна длина пароля (например, на ресурсе, аккаунт на котором пытаются взломать, длина пароля фиксирована или по каким-то причинам не является секретом) и когда все же некоторые позиции символов известны. Возьмем пароль P=«password». Множество его символов S_P={‘p’,’a’,’s’,’w’,’o’,’r’,’d’}. Проведем эксперименты:
Эксперимент А: известно
и позиции 2 символов.
Эксперимент B: известно
и длина пароля.
Эксперимент C: известно
, длина пароля и позиции 2 символов.
Заранее можно сказать, что мораль будет в следующем: не надо давать никакой открытой информации о пароле пользователя при входе или выносить на дальний план ее защищенность. Также не надо давать подглядывать подозрительным незнакомцам (особенно в шляпе и черных очках, уж тем более в плаще и с именем Ева). Это мы и демонстрируем на данном примере (в столбцах A, B, C приводится количество подходящих под описание паролей из базы RockYou):
На этом месте в нашей статье мы остановимся со сравнением сценариев A и B. Далее будет рассматриваться только сценарий А. Желающие могут проделать аналогичные вычисления для сценария B. Это будет полезно для сравнения этих двух подходов в сценариях, где pps будет угадываться с некоторого момента, а не собираться достаточная информация для 100% преодоления запроса.
Атака кейлоггинг + bruteforce с несколькими попытками
Теперь соберем в кучу все, что мы знаем (синергируем, так сказать). Рассмотрим, для примера, сценарий A. Постановка задачи в основе своей остается той же, но дополняется следующим образом: мы допускаем на каждом этапе (вне зависимости от наших знаний о пароле) использование bruteforce-атаки, также имеем в запасе попыток ответа на запрос до ее замены на другую (или, что лучше, до блокировки доступа к аккаунту или принудительного использования дополнительного этапа аутентификации (другого типа)). Здесь формула для вероятности
остается неизменной. Найдем долю запросов (размера
), в которых ровно
известных злоумышленнику позиций при условии, что он уже знает символы на
позициях пароля. Она выражается формулой (гипергеометрического распределения, упоминалась в предыдущем разделе):
Далее запишем выражение для доли запросов с известными позициями символов после
перехваченного запроса:
Если злоумышленник знает позиций в запросе после
перехватов, он может попытаться угадать оставшиеся
символов перебором. Тогда за
попыток ввода он может верно ответить на запрос с вероятностью:
Здесь обозначает вероятность того, что не более, чем за
попыток, злоумышленник сможет отгадать pps, зная в текущем запросе ровно
позиций символов. Очевидно, что формула для
имеет вид (
равна единице, если число возможных вариантов меньше числа попыток ввода):
Теперь остается построить графики зависимости вероятности успешно ответить на запрос pps от числа перехваченных запросов для некоторых наборов параметров, употребительных в реально существующих системах (левый график для алфавита (PIN), правый — для пароля из цифр и букв
;
и
соответственно):
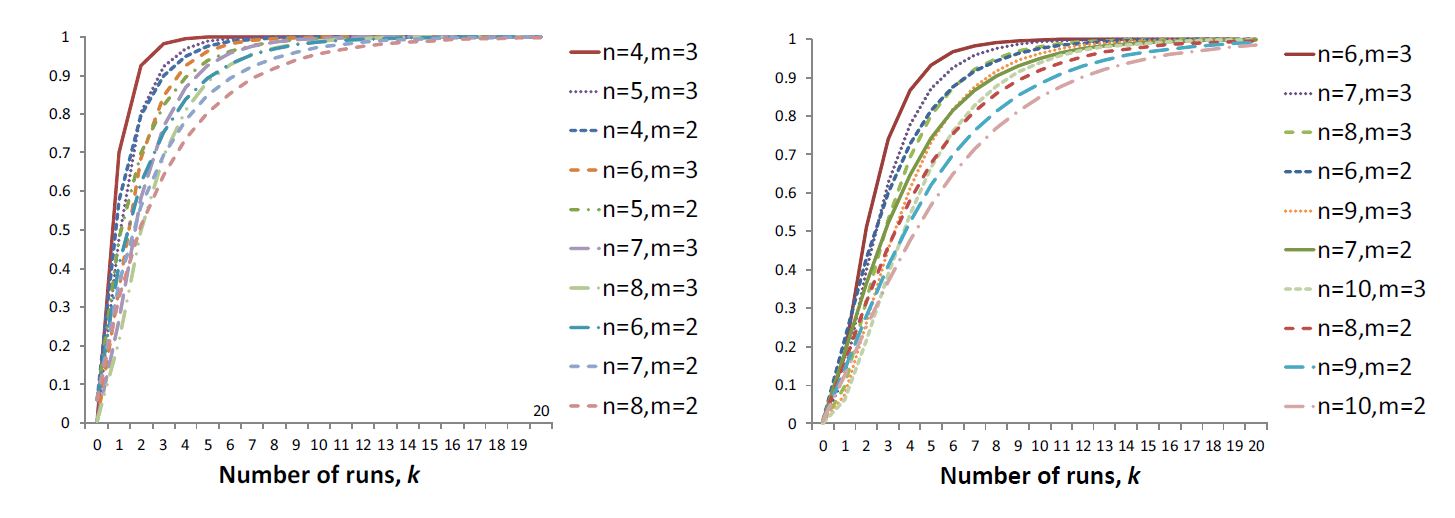
Видим, что результаты значительно лучше предыдущих (для взломщика), основанных на отдельно запоминании или bruteforce (важно отметить, что здесь еще есть попыток ввода). Например, здесь для PIN при
и
получаем, что вероятность успешной атаки превышает 50% только после
перехватов запросов. Для пароля из букв и цифр необходимо
перехвата.
Атака кейлоггинг + использование частоты встречи сочетаний символов на определенных позициях с несколькими попытками
Ведем огонь из всех орудий. Повторений символов в одном запросе вновь нет. Приведем грубую нижнюю оценку для вероятности взлома в этом случае. Используем данные из разделов выше для атаки с частотностью сочетаний символов и будем выбирать в своих попытках ввода самые распространенные из них. Приведем лишь численные значения для и
в случаях PIN (
) и пароля из букв и чисел (
) и сравним с предыдущим, bruteforce-вариантом:
Атака |
Параметр |
Вероятность взлома |
|
PIN |
пароль |
||
Кейлоггинг + bruteforce |
0.411 (0.838) |
0.096 (0.691) |
|
Кейлоггинг + словарь |
0.602 (0.904) |
0.252 (0.812) |
|
Закономерно получаем, что выбор наиболее распространенных вариантов сочетаний значительно увеличивают вероятность взлома pps. Числа становятся довольно пугающими, что говорит о том, что в реально существующих системах подбор параметров pps нужно проводить более тщательно. Ожидаемо, что защищенность увеличивается при увеличении размера словаря (например, добавлением больших букв и спецсимволов) и длины пароля
. Кроме того, размер запроса не стоит делать как большим (ведь о полном пароле утекает много данных), так и слишком маленьким, ведь в этом случае появляется хорошая возможность для подбора и лингвистического анализа.
Об общих выводах напишем чуть ниже, а сейчас перейдем к модельному примеру реализации pps с использованием схемы разделения секрета Шамира на языке python.
5. Модельный пример реализации pps на python

Реализуем pps с схемой разделения Шамира на языке python:
pps.py
import base64
import bcrypt
import os
import shamir
import time
import random
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.backends import default_backend
def generate_partial_password(password, min_parts_required,
work_factor,
salt_length=16):
"""Создадим pps"""
plen = len(password)
salts = []
keys = []
ivs = []
for i in range(plen):
salts.append(os.urandom(salt_length))
keys.append(bcrypt.kdf(password=password[i].encode('utf-8'), salt=salts[i], desired_key_bytes=32, rounds=work_factor)) # Key Derivation Function
ivs.append(os.urandom(16))
secret, shares = shamir.make_random_shares(minimum=min_parts_required, shares=plen)
encrypted = []
for (x, y), key, iv in zip(shares, keys, ivs):
backend = default_backend()
cipher = Cipher(algorithms.AES(key), modes.CBC(iv), backend=backend) # алгоритм AES + Cipher Block Chaining (CBC)
encryptor = cipher.encryptor()
ct = encryptor.update(y.to_bytes(32, byteorder="little")) + encryptor.finalize()
encrypted.append(ct)
output = []
for salt, iv, ct in zip(salts, ivs, encrypted):
output.append({'salt': salt, 'iv': iv, 'ct': ct[:16]})
secret = base64.urlsafe_b64encode(secret.to_bytes(16, "little"))
print(secret)
hashed_secret = bcrypt.hashpw(secret, bcrypt.gensalt())
return output, hashed_secret
def test_partial_password(password, p, hashed_secret, work_factor):
"""Проверка правильности введенных символов"""
shares = []
for k,v in password.items():
key = bcrypt.kdf(password=v.encode('utf-8'),
salt=p[k]['salt'],
desired_key_bytes=32,
rounds=work_factor)
backend = default_backend()
cipher = Cipher(algorithms.AES(key), # алгоритм AES
modes.CBC(p[k]['iv']), # Cipher Block Chaining (CBC)
backend=backend)
decryptor = cipher.decryptor()
ct = p[k]['ct'] + (0).to_bytes(16, 'little')
y = decryptor.update(ct) + decryptor.finalize()
y = int.from_bytes(y[:16], byteorder='little')
shares.append((k+1, y))
secret = shamir.recover_secret(shares)
secret = base64.urlsafe_b64encode(secret.to_bytes(16, "little"))
if bcrypt.checkpw(secret, hashed_secret): # проверка соответствия хешированного и нехешированного пароля
return True
else:
return False
if __name__ == '__main__':
password = input('Введите пароль:')
f = False
while f == False:
print(f'Введите размер запроса от 1 до {len(password)}')
try:
min_parts_required = int(input())
if min_parts_required > 0 and min_parts_required <= len(password):
f = True
else:
print('Неверный диапазон')
except ValueError:
print('Введите корректное значение')
print('Генерация секрета из пароля и "точек" для каждой буквы')
output, hashed_secret = generate_partial_password(password,
min_parts_required=min_parts_required,
work_factor=50)
print("Вывод:", output)
print("Хешированный секрет:", hashed_secret)
print('Проверка введенных паролей')
challenge = sorted(random.sample(range(0, len(password)), min_parts_required)) # запрос без повторений
response = []
print(f"Введите символы {[challenge[i] for i in range(min_parts_required)]}!")
i = 0
while i < min_parts_required:
input_char = input(f"Символ {challenge[i]}:")
if len(input_char) == 1:
response += input_char
i += 1
else :
print('Введите единичный символ')
pps = dict(zip(challenge, response))
start = time.time()
result = test_partial_password(pps, output, hashed_secret, work_factor=50)
print("Выполнение:", time.time() - start, "сек")
reply = "верны" if result else "неверны"
print(f"Введенные символы {reply}")shamir.py
from __future__ import division
import random
import functools
# 12-ое простое число Мерсенна
_PRIME = 2**127 - 1
_rint = functools.partial(random.SystemRandom().randint, 0)
def eval_at(poly, x, prime):
'''
Значение многочлена в точке x
'''
accum = 0
for coeff in reversed(poly):
accum *= x
accum += coeff
accum %= prime
return accum
def make_random_shares(minimum, shares, prime=_PRIME):
'''
Генерация случайных точек полинома
'''
if minimum > shares:
raise ValueError("восстановление секрета невозможно")
poly = [_rint(prime) for i in range(minimum)]
points = [(i, eval_at(poly, i, prime))
for i in range(1, shares + 1)]
return poly[0], points
def extended_gcd(a, b):
'''
Реализация расширенного алгоритма Евклида,
поиск x, y: ax+by=gcd(a,b)
'''
x = 0
last_x = 1
y = 1
last_y = 0
while b != 0:
quot = a // b
a, b = b, a % b
x, last_x = last_x - quot * x, x
y, last_y = last_y - quot * y, y
return last_x, last_y
def divmod(num, den, p):
'''
Вычисление num / den mod p = num * (den)^(-1) mod p
Возвращаемое значение: den * divmod(num, den, p) mod p == num
'''
inv, _ = extended_gcd(den, p)
return num * inv
def lagrange_interpolate(x, x_s, y_s, p):
'''
Нахождение y по данному x, зная n других точек (x, y)
k точек определяют многочлен степени k-1 или ниже
'''
k = len(x_s)
assert k == len(set(x_s)), "точки должны быть различны"
def MUL(vals): # MUL -- произведение аргументов
accum = 1
for v in vals:
accum *= v
return accum
nums = []
dens = []
for i in range(k):
others = list(x_s)
cur = others.pop(i)
nums.append(MUL(x - o for o in others))
dens.append(MUL(cur - o for o in others))
den = MUL(dens)
num = sum([divmod(nums[i] * den * y_s[i] % p, dens[i], p)
for i in range(k)])
return (divmod(num, den, p) + p) % p
def recover_secret(shares, prime=_PRIME):
'''
Восстановление cекрета по точкам
(x,y) - точки многочлена
'''
x_s, y_s = zip(*shares)
return lagrange_interpolate(0, x_s, y_s, prime)(*) За основу благодарю Jonathan Street
Настала пора подвести некоторые итоги.
6. Обсуждение и некоторые выводы
Частичные пароли были созданы для противостояния компрометированию пароля за один шаг в случае использования злоумышленником кейлоггинга или элементарного оффлайн-подглядывания. Частичные пароли могут дать пользователю некоторое время для смены пароля или блокировки аккаунта перед тем, как взломщик получит достаточную для уверенного взлома информацию. Данная модификация классической парольной аутентификации широко распространена в ряде стран мира, особенно в финансовой сфере, крайне чувствительной к потере аккаунта. В статье мы рассмотрели устройство и методы реализации pps, базовые типы атак на них. Несмотря на то, что частичные пароли хорошо справляются с атаками полного перебора и атаками полного восстановления пароля, но с условием перехвата запросов даже элементарные улучшения алгоритмов взлома показывают высокую эффективность против pps с используемыми на практике (крупными финансовыми компаниями) параметрами. Поэтому следует с большим вниманием относится к подбору параметров pps, чтобы сделать защиту действительно стойкой.
Частичные пароли являются простой и дешевой надстройкой над обычными паролями, которые в купе с другими этапами многофакторной аутентификации (такими, как использование дополнительного, полного пароля, привязка к номеру телефона, к почте, к другим аккаунтам, запрос некоторых данных о пользователе, использование биометрии и другие) позволяют эффективно бороться с утечкой пароля, что делает защиту аккаунта еще более сильной, а взлом аккаунта — бесперспективным занятием. Отдельной сферой, на мой взгляд, может стать использование pps в различных уличных терминалах и банкоматах в качестве защиты от считывания с них данных (скиммеры, вредоносное ПО, любопытствующих взгляд из-за плеча).
Вспомним полученные нами промежуточные результаты анализа pps. Во-первых, довольно неожиданно оказалось, что запросы с, возможно, повторяющимися позициями являются более устойчивыми к взлому*(внимание на постановку вопроса) почти во всем диапазоне числа перехватов запросов, чем решение без повторений (*в смысле полного восстановления пароля и получения известной комбинации в следующем запросе). Но все равно, запросы типа «введите 5,5,5 символы» звучат странно и уязвимо (особенно с малым алфавитом). В таких сценариях лучше делать запрос побольше и блокировать выбросы с большим числом повторов. Очевидно, не стоит менять запрос при каждой перезагрузке, ведь злоумышленник может выжидать имеющихся у него позиций. Само собой, стоит информировать пользователя о попытках входа.
Той части коммьюнити, которая заинтересовалась темой, предлагается расширить анализ pps, провести дополнительные выкладки и расчеты для случая B (они похожи на А) и, возможно, дополнить анализ другими типами атак. Возможно, "поиграть" с распределениями выпадения символов, как-нибудь обыграть проблему с самыми "проблемными" или легко угадываемыми позициями. Возможно, изменить или придумать новые форматы запросов. Безусловно, нужно дальнейший поиск правильных вопросов и грамотных ответов на них.
Общие рекомендации по подбору параметров pps (в принципе, универсальные): самое очевидное — выбор длинного и стойкого пароля, минимум - не qwerty и alex123, максимум - сгенерированного случайно. Размер запроса не стоит делать большим - таким образом быстрее набираются данные о полном пароле, но и не слишком малым - тогда повышается вероятность подбора pps. Таким образом, можно найти некоторый оптимальный размер запроса частичного пароля.
Однако есть и очевидные минусы pps: не каждый человек захочет запоминать пароль так, чтобы у него от зубов отскакивали все символы в каждой позиции. Не все смогут его запомнить, а постоянное черчение таблички с паролем и подписанными номерами букв во многом убивает саму идею такого технического решения, как и бумажка с паролем в записной книжке. Кроме того, хоть решение дешевое и, в определенном смысле, эффективное, все же не стоит использовать его как единственное средство защиты, а позаботиться о комплексной безопасности аккаунта. Хорошая новость в том, что все большее число крупных компаний вводит принудительную многофакторную аутентификацию или хотя бы выпускают поучительные брошюры о цифровой гигиене. Будем надеяться, что новости о крупных утечках аккаунтов все реже будут нас беспокоить. Было бы хорошо сделать все, что зависит от нас, как от пользователей, для защиты наших данных, не жалея нескольких, может быть, десятков секунд при регистрации и входе на свою страничку. Остальное — остается на совести компании.
Спасибо всем, кто проявил интерес к данной статье. Надеюсь, что информация, изложенная мною, была полезной. До новых встреч!
Источники:
Mourouzis, Theodosis & Wojcik, Marcin & Komninos, Nikos. (2016). On The Security Evaluation of Partial Password Implementations.
Aspinall, David & Just, Mike. (2013). «Give Me Letters 2, 3 and 6!»: Partial Password Implementations and Attacks. 7859. 126-143. 10.1007/978-3-642-39884-1_11.
Adams, Anne & Sasse, Angela & Lunt, Peter. (1999). Making Passwords Secure and Usable. 10.1007/978-1-4471-3601-9_1.
Комментарии (32)

belch84
02.12.2021 11:38+5Не совсем по теме, но публикация напомнила мне о реальной проблеме, которая возникала у меня лично. Некоторые из паролей, которые я использую, являются русским словами, набираемыми в английской раскладке клавиатуры (кажется, я такой не один). При работе на десктопе/ноутбуке это удобно, но неудобно при наборе пароля на телефоне/планшете (экранные клавиатуры на них не показывают соответствия кириллических/латинских символов). Когда-то у меня была необходимость использовать планшет, находясь очень далеко от дома и используя бесплатный Wi-fi. Для набора паролей пришлось заранее распечатать и вложить под чехол планшета изображение клавиатуры с русскими/латинскими символами.
Кстати, русские пароли в таком виде удобны и для применения в виде частичных, поскольку для русскоязычного удобно отсчитать нужные символы в уме, не записывая пароль на бумажке
TheDenis
02.12.2021 12:44+1Тоже когда-то пользовался этой методиков. До полного перехода на менеджер паролей. Но надо понимать, что при установлении (или при обоснованном предположении о вашем родном языке), такой подход увеличит сложность атаки по словарю всего в два раза.
Кстати, о менеджерах паролей. Я далеко не все из них смотрел, но широкой поддержки PPS я не видел. Это, как мне кажется, будет серьёзной проблемой для широкого внедрения частичных паролей. Да и реализовать автозаполнение в этом случае будет очень нетривиальной задачей.

HenryPootle
03.12.2021 10:19Но надо понимать, что при установлении (или при обоснованном предположении о вашем родном языке), такой подход увеличит сложность атаки по словарю всего в два раза.
В сочетании с заменой букв на символы или цифры, а так же выбор редких слов нивелирует эти уязвимости. Как вам, например, "Ону4иношен#е"?

TheDenis
03.12.2021 10:25Лично мне – плохо :) Я по-другому запоминаю пароли. Мне важен ритм, как оно неразрывно "произносится" в голове. И l33t code не вписывается в эту схему.

qyix7z
03.12.2021 12:09о менеджерах паролей
KeePass2Android предлагает «быструю разблокировку» по трем последним символам пароля с одной попыткой ввода. При ошибке требует полный пароль. Я понимаю, что это несколько другое, но тем не менее.

ITficator
03.12.2021 21:38Под Android использую приложение Keepass2Android, но, как правило, пользуюсь копи-пастом вместо интегрированных функций автозаполнения. Также много лет таскаю от смартфона к смарфону безопасную клавиатуру для паролей (вводишь на русском, пишет латиницей) без рекламы и вообще без выхода в Интернет. Она очень эргономичная. Этой клавиатуры давно нет в PlayMarket, к сожалению. Где-то на 4pda встречал её, но не вспомню.

belch84
02.12.2021 13:02Но надо понимать, что при установлении (или при обоснованном предположении о вашем родном языке), такой подход увеличит сложность атаки по словарю всего в два раза.
Это, в основном, просто удобнее для запоминания

amarao
02.12.2021 15:33+3Hellenic bank пошёл ещё "мудрее". Они спрашивают (!) последние две цифры пин-кода карты. При логине на сайт. /facepalm x3.
Лучше бы otp сделали.

emaxx
03.12.2021 05:59+1Странный какой-то анализ...
Но все же, запросы вида «Введите символы 1,1,3» или, тем более, «Ждем позиций 7,7,7» будут выглядеть несколько странно.
Это не просто странно, а фактически уменьшает длину запроса (потому что для атакующего эти два запроса - то же самое, что "1,3" и "7", соответственно), повышая вероятность успешного брутфорса выше. Например, при запросе "7,7,7" атакующему, вообще не знающему ничего об искомом пароле, надо просто угадать один символ из алфавита - что, очевидно, гораздо менее безопасно обычной схемы с несколькими запрашиваемыми символами.
Видим, что хотя на первых нескольких попытках вероятность ответа чуть ниже у сценария A (так как в запросе не может быть повторов), но для всех остальных значений сценарий B имеет значительно более высокую стойкость к взлому.
Но ведь формулы, приведённые в статье перед этой фразой, говорят не о стойкости к взлому, а о - цитата - "вероятность того, что в очередном запросе будут позиции символов, которые ему уже известны". Что, как бы, и так понятно из неформальных рассуждений: если схема такова, как "B", что она иногда спрашивает у пользователя меньше символов, то и кейлоггер будет в среднем накапливать меньше данных, да и более короткий запрос имеет меньшие шансы пересечься с уже накопленным. Только вот как это коррелирует с общей безопасностью схемы? Мы же ухудшаем устойчивость одного запроса к взлому: во-первых, атакующему проще угадать ответ на один запрос из-за его возможно меньшей длины (см. начало комментария), а, во-вторых, ценность каждого утекшего символа растёт (пользуясь вашими примерами - для ответа на запрос "7,7,7" атакующему достаточно знать один-единственный утекший символ №7).

AiratNazmiev Автор
03.12.2021 20:10+1Само собой, выпадение 777 - это просто угадывание одного символа на позиции 7. Это не вполне хорошо, в некоторых смыслах, стоит как-то подправить эту схему.
Стойкость схемы с повторениями оказалась эффективнее в контексте восстановления пароля полностью. Вариант с дополнительным угадыванием, к сожалению, в случае дополнительного угадывания не рассматривался .Впрочем, нет особой проблемы сделать это, может быть, на досуге стоит посмотреть. Или кто-то из читателей может этим заняться, если будет интересно.
Результат наверное, естественный (но если задуматься, то не такой уж и тривиальный), ведь просто ниже вероятность выпадения всего набора букв (возможно, придётся долго ждать последних недостающих символов из-за некоторых повторений в запросе). Само собой, с учётом угадывания, результат может измениться, оптимизация параметров должна быть более тонкой. Кроме того, уж очень слабые комбинации можно просто блокировать и не запрашивать или ограничивать минимальное число уникальных символов в запросе. Так что открывается большой простор для оптимизаций параметров, но анализ при этом кардинально не усложняется. Ещё, эта проблема может дополнительно купироваться на коленке увеличением словаря (но не им единым).
Теперь стоит сказать, для чего нужно отдельное рассмотрение такой атаки: атаки с полным восстановлением пароля или атаки с уверенным ответом на следующий запрос (гиперболизированный пример). Злоумышленник поставил перед собой цель во что бы то ни стало взломать аккаунт некоего гражданина. Допустим, он получил доступ к основному паролю своей горе-жертвы (подсмотрел из-за спины или просто скопировал из какого-нибудь блокнотика на компьютере), доступ к телефону/почте (почему бы и нет) и узнал девичью фамилию троюродной бабушки по отцовской линии. Ему для беспрепятственного доступа к аккаунту не хватает лишь ответа на частичный пароль, который ему не удалось пока узнать. Поэтому он установил на компьютер жертвы кейлоггер или физически поставил на его клавиатуру свою реплику-шпион (или не на компьютер, а на его любимый терминал в ТЦ). Теперь злоумышленник затаился и ждёт, пока он не накопит информацию о частичном пароле, при каждом входе жертвы он получает новую информацию (а пароль этот будет достаточно длинным, с оптимальными параметрами).Patience... Don't do anything stupid.
Он не хочет рисковать: если попытаться войти в аккаунт и провалиться, то жертва сорвётся и поменяет пароль или заблокирует свой счёт или свою страничку... Дожидается и получает прямой доступ в аккаунт своей жертвы.
Менее вероятно, что злоумышленник сможет получить полный набор данных о большом числе людей, чтобы иметь возможность поиграть в статистику.
В таком контексте были проведены рассуждения в матмодели, вплоть до раздела "Атака кейлоггинг + bruteforce"
Возможно, сценарий и искусственный, но, всё же, такое решение действительно создает некоторые дополнительные преграды, против которых некоторые другие способы защиты бессильны (например, при ограниченном бюджете и возможностях).

emaxx
03.12.2021 20:20Предложенная attack surface не очень понятная. Если мы рассматриваем только этот вид атак, то самой выгодной станет схема "спрашивать по одному символу пароля". В вашей модели attack surface (с затаившимся взломщиком) это даст самое медленное раскрытие информации, хотя в реальности, разумеется, это абсолютно небезопасная схема, потому что любому "не таящемуся" атакующему достаточно будет угадать один символ для успешного взлома. Ваша схема "B" - это просто один шаг в направлении этой схемы, но уже этот шаг понижает общую устойчивость к взлому.

AiratNazmiev Автор
03.12.2021 20:38+1Я, в большей части, вижу (точнее, недавно увидел) pps как дополнительную меру защиты аккаунта. Собственно, она в существующих решениях так и используется. Да, возможно, в гиперболе выше самым лучшим решением будет посимвольный запрос и действительно так и стоит бороться с настойчивыми и находчивыми взломщиками. Но интуиция может легко обмануть, на мой взгляд, запрос по одному символу будет менее безопасным даже в таком контексте. Это можно проверить (я пока не проверял, могу ошибаться).
В реальности используются другие параметры, характерные числа и были рассмотрены выше (которые, к сожалению, имеют сомнительную стойкость во многих смыслах). Задача проста, но, на удивление, очень мало людей ей уделяют внимание, непропорционально тем надеждам, которые на pps возложены (создавая при этом некоторый дискомфорт пользователю). Было бы неплохо плотнее взяться за эту тему.
Мотивация к рассмотрению B в том, что это элементарная модификация A, к которой легко перейти почти задаром и которая легко интерпретируется.
На русском языке я не нашел ни одного шага, лежащего на расстоянии вытянутой руки. Так что можно делать шаги дальше. Тем более, что модель совсем несложная.

emaxx
03.12.2021 23:10Неужели вы не видите противоречия между тем, что, как вы согласились, предложенный сценарий "B" приближает нас к варианту с односимвольным челленджем, и очевидной небезопасностью односимвольного челленджа? Что условную устойчивость к кейлоггингу мы покупаем ценой компроментации всей схемы, фактически укорачивая запрашиваемые пароли?

AiratNazmiev Автор
04.12.2021 00:06Я много раз писал о том, что нет смысла использовать эти пароли в отрыве от других средств защиты, хотя бы с обычным паролем. Тогда условная устойчивость pps к кейлоггингу с безусловной уязвимостью к угадыванию дополняется безусловной устойчивостью пароля к подбору, однако имеющего абсолютную уязвимость к кейлоггингу. В этом случае даже односимвольный челлендж будет лучше, чем ничего

emaxx
04.12.2021 01:30Это забавно, что вы упомянули про "ничего", потому что в вашей модели атак, как раз-таки, "ничего" будет идеальной системой защиты! Потому что если сервер не спрашивает ни одного символа пароля, то и кейлоггер не запишет ни одного символа - вот и идеальный результат в предложенной вами attack surface. По меньшей мере тут уже можно понять, насколько абсурден анализ, проводимый из таких предпосылок...

AiratNazmiev Автор
04.12.2021 02:25Прошу прощения, но я считаю, что Вы уже передёргиваете. Если будет "ничего", то пользователь вводит свой пароль и в тот же момент его теряет. Если есть частичный пароль, то этого не произойдёт с вероятностью, отличной от 1.
Я Вам скажу, что подобный абсурдный анализ, ещё и с некоторыми помарками, был опубликован в рецензируемых журналах (теперь уж пришлось апеллировать к авторитетам). Во многом на них и основано эссе. Но я лично не позиционирую этот текст как исчерпывающее руководство к действию, а как повод узнать или задуматься про такой тип паролей, так как не получится найти источников на русском языке по этой теме.
Скажем так, среди прочего, предпосылка - это то, что такие пароли активно используются уже давно и используются по сей день. Проблема в том, что нужно проводить подбор параметров более тщательно, чем это делают в настоящий момент, потому что даже против простых типов атак, связанных с кейлоггингом они неэффективны, не выполняют своей роли. Хотелось тут донести, что стоит подправить параметры, чтобы вообще вся эта затея имела смысл. А то выходит, что пользователи финсектора страдают ни за что.
Я остановился на анализе такого типа. Исчерпывающий анализ заслуживает какой-нибудь небольшой монографушки. Я и не претендовал на всеобъемлющее исследование, на последние истины. Но в рассмотренных постановках, где производилось сравнение двух методов, были сделаны некоторые выводы и было упомянуто, в каких предпосылках. Можно спорить о них, но замах был ровно на то, о чём и было написано. Предоставлен некоторый простой и занимательный метод, как можно посчитать некоторую несложную комбинаторику. Быть может, кто-то захочет покопаться в этом вопросе самостоятельно.
Спасибо за Ваши комментарии, я думаю, что теперь желающие использовать pps люди ещё раз взвесят все за и против перед тем, как выкатывать что-то в продакшен. Возможно, кто-то захотел бы использовать текст как кулинарную книгу, чего бы делать не стоило.

AiratNazmiev Автор
03.12.2021 21:51"Вариант с дополнительным угадыванием, к сожалению, в случае дополнительного угадывания не рассматривался" - опечатка, должно было быть "Вариант с дополнительным угадыванием, к сожалению, в случае запросов с повторениями не рассматривался"

emaxx
03.12.2021 23:04Так ведь без этого какие выводы можно делать о реальной устойчивости схемы? Упражнения на комбинаторику в статье проделаны хорошие, только вот к выводу "сценарий B имеет значительно более высокую стойкость к взлому" они никак не приводят. В лучшем случае это введение читателей в заблуждение, в худшем - кто-то пойдёт на поводу у статьи и эту, простите, ерунду в реальный продакшен выкатит...

AiratNazmiev Автор
03.12.2021 23:58В выводе я отдельно отметил, в каком сценарии это действительно так. Цитата "сценарий B имеет значительно более высокую стойкость к взлому" взята из раздела, где недвусмысленно и не один раз описано, в каком случае и при каких предположениях одна схема лучше другой. В выводе, опять же, сделана ремарка о том, в каком смысле и что лучше. Возможно, что при беглом чтении может возникнуть желание сделать обобщение или вообще принять, что частичные пароли - это панацея. Но это не так. Я старался не быть категоричным и уж точно не рекламировал pps, никакого интереса в этом не имею.
На всякий случай ещё раз дополню общий вывод, чтобы уж наверняка не ввести читателей в заблуждение.
Можно еще добавить призыв к дальнейшему изучению, в качестве упражнения и досуга.
К сожалению, достаточно много людей уже выпустили в продакшен эту ерунду, многие этой ерундой пользуются, в выборе параметров не руководствуясь никакими расчётами и выкладками. Кто-то из пользователей и не задумывался, зачем такую изощрённую пытку вообще придумали. Возможно, кого-то и остановят полученные результаты от использования в продакшене
И да, я люблю упражнения на комбинаторику. Может быть, кому-нибудь эта страничка будет интересна в контексте занимательных формул и фактов.

emaxx
04.12.2021 01:24Речь не про частичные пароли, а про ваш вывод, что сценарий B более защищён, чем другой. Повторюсь, этот вывод является манипуляцией: на основе одной формулы, которая оценивает только один из аспектов безопасности, делается вывод об общем превосходстве этой схемы над другой. Однако это вывод так же неверен, как, например, говорить "давайте предположим, что атакующий не будет использовать атаки по словарю" и на основе этой предпосылки делать рекомендации о применении схем безопасности.

AiratNazmiev Автор
04.12.2021 03:14Я внёс некоторые дополнительные изменения в текст, чтобы уж точно исключить возможное неправильное толкование.
Общего превосходства не доказано, как и не показано, почему вообще рассмотрено только две схемы (одна - используется в реальности, другая - её простая модификация). И почему вообще именно частичные пароли нужны именно в таком виде (возможно, кто-то придумает альтернативу).
Да, предпосылка такая. Но в тех сравнениях и не шла речь про атаки с подбором. Там давались либо точные ответы на новый запрос, либо полное восстановление пароля. А актуальность и распространенность такого сценария очевидна и показана на примерах, особенно в случае роли pps в качестве дополнительного средства защиты (а другое и не имеет особого смысла). Так что решалась поставленная задача, которая имеет как практический, так и некоторый теоретический интерес (занимательные формулы на поупражняться, добрая затея), в указанных предпосылках система описывается некоторой моделью, которая исчерпывающе закрывает вопрос с этим сценарием (напомню, он даже изолированно имеет большое значение). Так что манипуляций нет и речи о них быть не может. Все модели неверны, но некоторые из них полезны. Полезность этой - мною уже много раз описана и в тексте, и в комментариях. Другая польза в том, что можно будет продолжить анализ и покопаться в подробностях не в одиночку, а той части коммьюнити, которой показалась занятной модель и результаты или тем, кто заинтересовался практической стороной дела. Кроме того, показана очевидная уязвимость текущих частичных паролей, нет никакого смысла делать запросы и целый пароль в pps такими маленькими.
Пожалуй, мне больше нечего сказать.

nsmcan
03.12.2021 07:56+2Однако есть и очевидные минусы pps: не каждый человек захочет запоминать пароль так, чтобы у него от зубов отскакивали все символы в каждой позиции.
На мой взгляд, с этого можно было бы начать и отбросить все остальные выкладки. При наличии выбора, я бы избегал пользоваться сайтами с такой аутентикацией

Neusser
03.12.2021 14:52+1А что вас так пугает? У меня в одном банке есть такой способ. Не могу сказать, что испытываю какие-то проблемы с тем, что не могу сходу назвать какой символ на какой позиции. Я даже сам пароль сходу не назову, не говоря уже об отдельных символах на определенных позициях.


itsoft
Вы много пишите про решение, но мало уделили актуальности проблемы. В диссертации актуальность проблемы надо доказать. И вот с ней большой вопрос.
Многофакторная авторизация решает проблему куда лучше, чем напрягать пользователя вводить какие-то отдельные буквы.
Система должна оставаться удобной. Аппаратные генераторы чисел, защита по IP-адресу, алгоритмическая зависимость действий от дня недели, числа месяца, самого месяца, см. habr.com/ru/company/itsoft/blog/581154
А пароли все копипастят из хранилок паролей. Пароль — это только один фактор. Нужны и другие.
Neusser
О какой диссертации речь?
itsoft
Тут статья со списком литературы, поэтому напомнило диссертации. Но в статье тоже полезно аргументировать наличие проблемы. Решение может быть абсолютно верным, математика правильная, но решать проблему, которой в действительности нет или проблема решается гораздо более простым способом. О чём я и написал.
Статический пароль — это слабая защита. Нужен динамический — аппаратный генератор чисел, СМС и прочее. А описанный метод — можно расширить до таблицы кодов на бумажке или до книги какой-то: страница номер, строка номер, вторая буква третьего слова.
AiratNazmiev Автор
Актуальность этого вопроса состоит хотя бы в том, что такие пароли широко используются реальными компаниями. Ясно, что таким образом решается проблема кейлоггинга, но хотелось бы посмотреть, насколько же такой подход реально эффективен. Видимо, англичане находодят pps удобными в некотором смысле.
К сожалению, не все ресурсы предоставляют возможность использовать двухфакторную аутентификацию. Возможно, сам человек не хочет оставлять лишние личные данные, номер телефона на этом сайте. А использование pps не требует никакой допинформации, легко в реализации. Возможно, в простеньких системах оно может иметь какое-то весомое значение как отдельный тип защиты.
Кроме того, можно представить ситуацию (пусть маловероятную), когда злоумышленник получил доступ к почте и к телефону (уж очень он хотел взломать некоторого гражданина), тогда частичные пароли могут выступить последней преградой на его пути. Может быть, седьмой замочек и не откроется.
Ещё вот такой важный сценарий: помнится, одно время очень популярны были скиммеры для банкоматов. Ввёл пинкод, карту считали. А при снятии денег по какой-то причине не просят звонить куда-то или снимать биометрию (пока что). Так что частичные пароли также могут иметь место в системах, в безопасности которых человек неуверен.
Таким образом, есть проблема - есть некоторое решение, которое в определенных условиях и в определенном смысле эффективно, более того, уже реально используется.
Список литературы никогда не бывает лишним. Можно обратиться к первоисточникам и почитать поподробнее.
Само собой, это не диссертация) Популярное эссе на тему с схемами и мемами, с некоторой долей наукообразия. Вряд ли бы диссертационная комиссия оценила моё желание рассказать им про то, что такое вероятность или элементраная комбинаторика.
itsoft
Да вот и получается, что идёт сдвиг в сторону неправильного решения. Вместо того, чтобы поддерживать генераторы, хотя бы программные, изобретают какие-то велосипеды. Есть Яндекс, Гугл, майкрофосфт аутентификаторы. Ставите себе на смартфон и вот почти аппаратный токен. И телефон светить не нужно.
На мой взгляд, главная проблема, что информационные системы игнорируют это решение. Хотя его внедрять делать нечего.
Tarakanator
Аунтификаторы может и есть, но аутентификация кривая. Я только начал это изучать
Дано: аппаратный ключ с поддержкой u2f, fido2 задача: попробуем аутентификацию без пароля.
(вариант с СМС не рассматриваю это костыли)
Яндекс: ставь наш аутентификатор, универсальные мы не поддерживаем. и только 2-х факторная.
Гугл: 2-х факторная аутентификация ок. Но в некоторых случаях я буду спрашивать только пароль(например при запросе установке приложения на телефон, когда запрос идёт с ПК) хотя казалось бы логичнее спрашивать 2-й фактор. Я даже поддерживаю безпарольную аутентификацию... но только если у вас есть 2 ключа. С одним никак. P.S. А ещё я похоже нашёл баг. Один и тот-же ключь нельзя дважды привязать к 2-х факторной аутентификации. Привязал, выключил 2-х факторную, второй раз уже не привязывается.
Майкрософт: поддерживаю даже безпарольную аутентификацию... но только через облако.
Steam: поддерживаю только собственное приложение. и только 2-х факторная.
Итого: беспарольная аутентификация 1/4(на самом деле меньше, т.к. сюда не вошли те, кто не поддерживает даже 2-х факторную аутентификацию) и то костылями.
2-х факторная... у всех с костылями.
Neusser
эти велосипеды изобретены еще до появления всяких аутентификаторов. И почему вы боитесь засветить свой телефон? Да и при чем тут вообще телефон?
itsoft
Про засветить телефон не я писал. Но мысль правильная. Зачем его светить? К тому же генератор чисел надёжнее смс. СМС к тому же денег стоят и приличных.
eugeneb0
Многофакторная аутентикация (одним из вариантов которой, если подумать, является та же проверка IP-адреса) -- это всегда внесение в систему дополнительных внешних зависимостей. По определению, потому как она должна проходить по независимому каналу.
Но чем больше зависимостей, тем выше вероятность, что какие-то из них будут использованы во зло. Не взломаны "хакерами", а именно недобронамеренно использованы самими хозяевами. Зачастую во имя самых светлых идеалов. Закрыть телефонный номер, потому что с него был разослан "запрещённый контент". Заблокировать почтовый адрес, потому что странно себя повёл. Не выслать товар, потому что заказан с непривычного айпи. Ну и т.п. И вот суммарная надёжность (с точки зрения конечного потребителя) многофакторных схем начинает падать. И будет падать, пока не сравняется с "наихудшей альтернативой", не имеющей внешних зависимостей. То есть... паролями.
У паролей, конечно, есть слабости. Труднозапоминаемые пароли люди пишут в менеджеры, что сводит безопасность схемы на нет. Легкозапоминаемые легко подбираются. НО! Вот как раз таки схема "частичного пароля", применённая к легкозапоминаемым, но длинным фразам, в значительной степени эту трудность устраняет.
Поэтому мне лично данная статья кажется крайне важной, а направление -- весьма перспективным. Не побоюсь сказать даже, в мировом масштабе.
Ведь схема <имя, пароль> -- это последнее ещё существующее средство для пользователя заявить свою "идентичность", контролируемое самим пользователем, а не Кем-То Третьим. Цифровой мир, где не осталось этого средства, будет очень страшным, управляемым лишь немногими игроками, и унылым местом. Пароли не просто рано выкидывать на свалку, за их сохранение надо бороться.