Подходы к квантовому шифрованию изображений / forpes.ru

Главная
Подходы к квантовому шифрованию изображений

Подходы к квантовому шифрованию изображений +22

12.12.2021 00:42

h_cthulhu 2 2300 Источник

В настоящее время практически во всех сферах жизнедеятельности человека получают широкое распространение информационные технологии. Как правило, мультимедиа включает в себя текст, аудио, изображение и видео. Среди этих четырех информационных форматов более привычны для восприятия человека изображение и видео, которое, в частности, можно рассматривать как серию изображений. Поэтому методы, направленные на работу с изображениями, имеют большое значение в области обработки информации.

С развитием квантовых вычислений появилась новая ветвь развития в этой области, а именно квантовая обработка изображений (англ. Quantum Image Processing, QIP), которая привлекает к себе всё больше внимания. Разрабатываемые алгоритмы QIP сочетает в себе квантовые вычисления вместе с цифровой обработкой изображений и оказываются более производительными по сравнению с современными классическими вариантами. Если рассматривать QIP с точки зрения защиты информации, то выделяют три основных направления: водяные знаки, стеганография и шифрование изображений. О последнем направлении как раз пойдёт речь в этой статье.

Квантовые биты

Перед тем как перейти непосредственно к шифрованию стоит упомянуть, с чем мы работаем в квантовых компьютерах. Для кодирования информации вместо обычных бит используются квантовые биты, или кубиты, — наименьшая единица информации в квантовом компьютере, используемая для квантовых вычислений. Как и биты, кубиты могут принимать значения 0 и 1, но отличие заключается в том, что кубит находится в суперпозиции сразу двух этих состояний. После создания кубита с ним можно работать посредством квантовых логических элементов, то есть менять вероятности его состояний, а так же запутывать его с другими кубитами, тем самым создавая корреляцию между их состояниями, что невозможно в классическом случае. Так как после измерения кубит схлопывается в одно из его собственных состояний, то во время операций с ним нельзя узнать его промежуточное состояние. С точки зрения количества информации система из кубитов может вместить себя экспоненциально больше информации. Однако стоит учитывать, что экспоненциальное увеличение пространства состояний системы не обязательно приводит к экспоненциальному росту вычислительной мощности в связи со сложностью кодирования и считывания информации.

Общие принципы квантового шифрования изображений

К шифрованию изображений выделяются такие требования как высокая скорость вычислений (в реальном времени) для таких приложений, как видеоконференцсвязь; высокая точность, например в точной диагностике заболеваний в телемедицине и другие. Стремясь удовлетворить некоторые или большинство из этих требований, технологии квантового шифрования изображений (англ. Quantum Image Encryption, QIE) можно в широком смысле классифицировать как стратегии, основанные на пространственной или частотной области [1]. Обобщенная схема QIE представлена на рисунке 1.

Рис. 1. Общий подход к шифрованию квантовых изображений

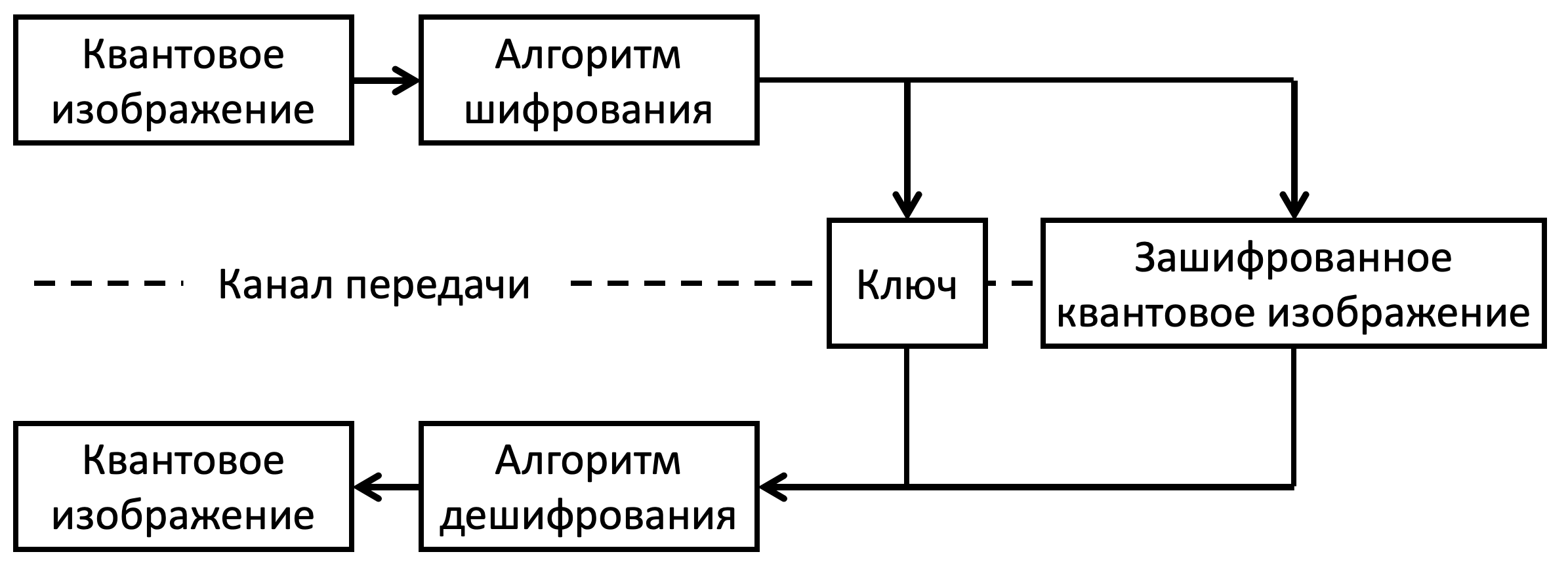
Информация относящаяся к пространственной области квантового изображения описывается расположением пикселей в нем и значениях в этих пикселях, то есть цвете. Следовательно, алгоритмы QIE, нацеленные на работу в пространственной области, в основном сосредоточены на этих двух параметрах. К методам, использующим данный подход, относятся скремблирование (преобразование положений пикселей для нарушения порядка в изображении), замещение (преобразование значений пикселей для изменения статистических свойств зашифрованного изображения), а также их объединение. В качестве примера рассмотрим алгоритм, имеющий меньшую сложность относительно других алгоритмов.

Квантовое шифрование с ключом-изображением

В этом алгоритме ключ-изображение и исходное изображение, которое должно быть зашифровано, представлены моделью NEQR (Novel Enhanced Quantum Representation). NEQR использует две запутанные последовательности квантовых битов для хранения информации о положении и информации о цвете изображения размера $H \times W$

$|C_{YX}\rangle=|C_{Y X}^{0} C_{Y X}^{1} \ldots C_{Y X}^{q-2} C_{Y X}^{q-1}\rangle$ — кодирование цвета в диапазоне $0 \sim 2^q-1$ ,

$|YX\rangle=|y_0y_1 \ldots y_{h-1}\rangle|x_0x_1 \ldots x_{w-1}\rangle$ — кодирование положения пикселя.

В этих выражениях $C_{YX}^i\ , x_i\ , y_i \in\{0,1\}, \ h=\left\lceil\log _{2} H\right\rceil, \ w =\left\lceil\log _{2} W\right\rceil$ . Таким образом, квантовое изображение состоящее из $H \times W$ пикселей в градациях серого в модели NEQR состоит из h+w+q кубитов и представляется следующим образом:

$|I\rangle=\frac{1}{\sqrt{2}^{h+w}} \sum_{Y=0}^{H-1} \sum_{X=0}^{W-1}\mathop{\otimes}\limits_{i=0}^{q-1}\left|C_{Y X}^{i}\right\rangle|Y X\rangle.$

Далее будем считать, что геометрические размеры изображения являются степенью двойки для некоторого упрощения формул (в противном случае, в пикселях выходящих за рамки изображения просто передается неиспользуемая информация любого цвета).

Сам алгоритм шифрования состоит из трех шагов и изображен на рисунке 2:

Рис. 2. Шифрование с ключом-изображением

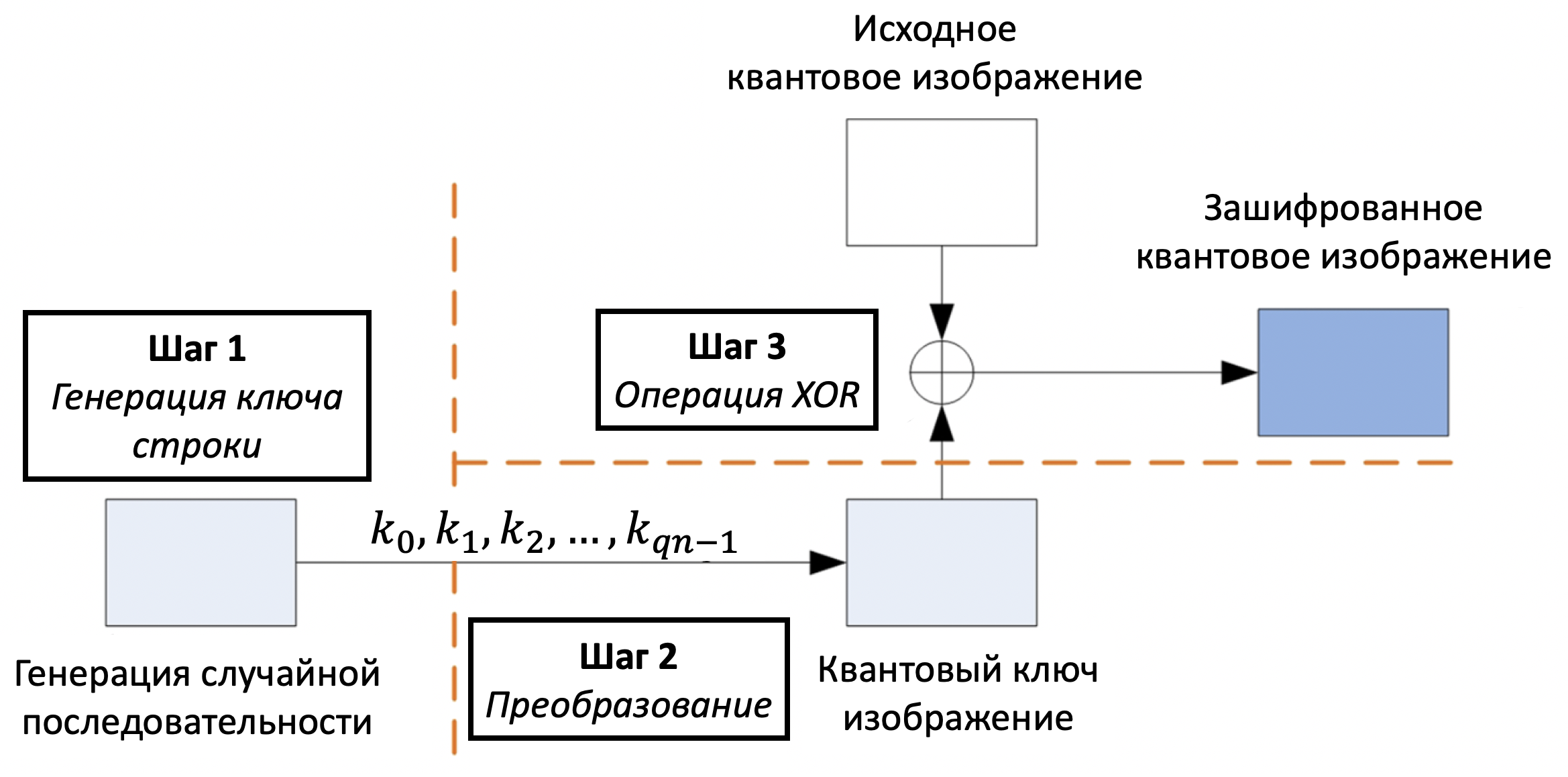
Шаг 1. Генерация ключа-строки.

Используя любой генератор случайной последовательности получаем строку $\{k_0\ ,k_1\ ,...,\ k_{qHW-1}\}$ , где $k_{i} \in\{0,1\},\ i \in[0,\ qHW-1]$ .

Шаг 2. Преобразование в ключ-изображение

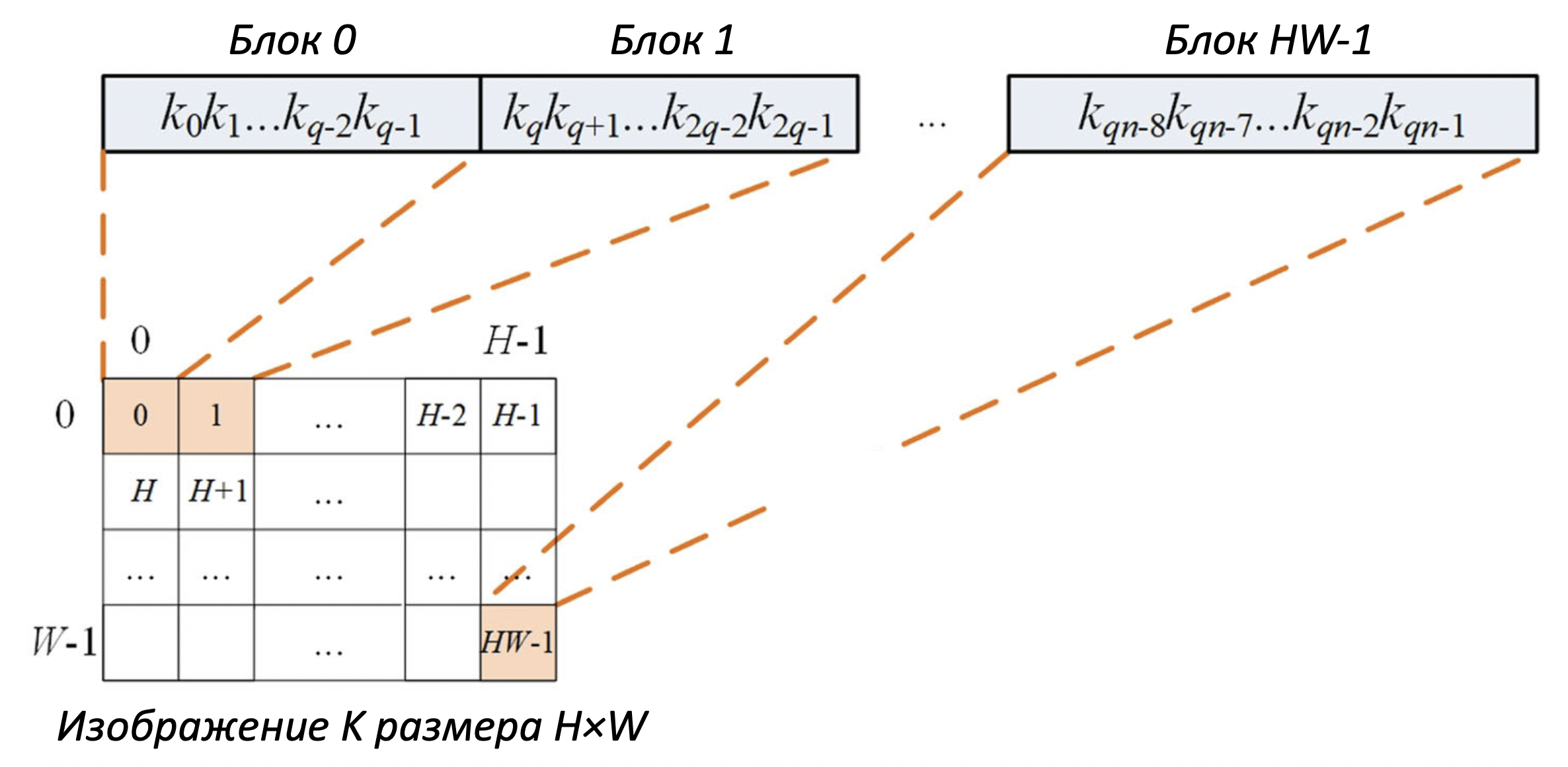
Говоря простыми словами, строка разбивается на блоков размера каждый, затем эти блоки используются для кодирования цвета в каждой позиции ключа-изображения, имеющего те же размеры, что и оригинальное изображение, что демонстрируется на рисунке 3. Процесс инициализации в меньшей степени относится к самому алгоритму, поэтому его подробное описание через формулы квантовой физики можно прочитать в оригинальной работе [2].

Рис. 3. Преобразование строки в ключ-изображение

Шаг 3. Операция XOR

На последнем шаге мы применяем операцию XOR к оригинальному изображению $|I\rangle$ и ключу-изображению $|K\rangle$ для получения зашифрованного изображения $|M\rangle$ .

XOR

$\begin{aligned} |I\rangle \oplus|K\rangle &=\frac{1}{\sqrt{2}^{h+w}} \sum_{Y=0}^{H-1} \sum_{X=0}^{W-1} \mathop{\otimes}\limits_{i=0}^{q-1}\left|C_{Y X}^{i}\right\rangle|Y X\rangle \oplus \sum_{Y=0}^{H-1} \sum_{X=0}^{W-1}\mathop{\otimes}\limits_{i=0}^{q-1}\left|K_{Y X}^{i}\right\rangle|Y X\rangle \\ &=\frac{1}{\sqrt{2}^{h+w}} \sum_{Y=0}^{H-1} \sum_{X=0}^{W-1} \mathop{\otimes}\limits_{i=0}^{q-1}\left|C_{Y X}^{i} \oplus K_{Y X}^{i}\right\rangle|Y X\rangle \\ &=|M\rangle. \end{aligned}$

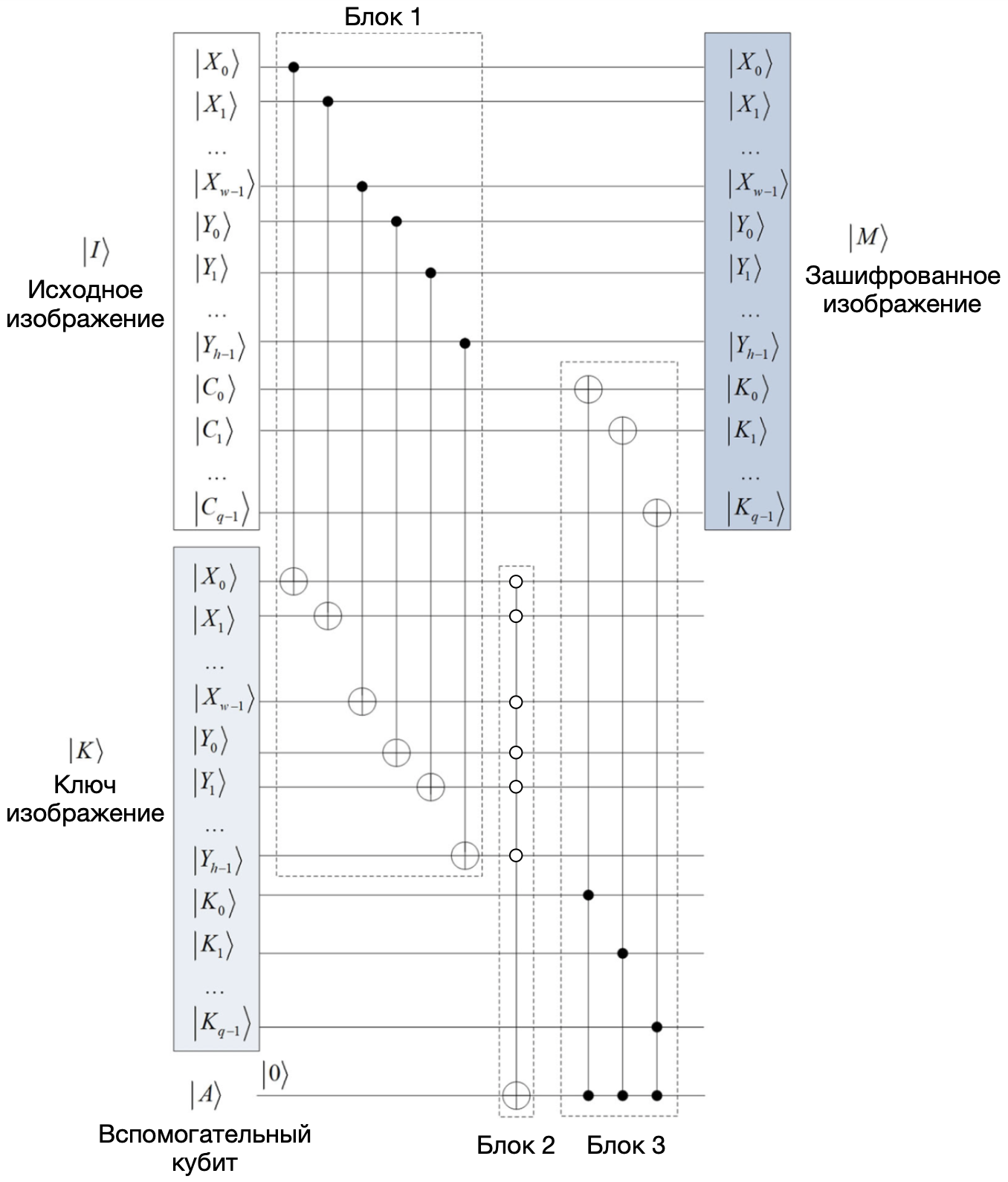
Квантовая схема для операции XOR на изображениях $|I\rangle$ и $|K\rangle$ , изображенная на рисунке 4, разделена на три блока:

Блок 1 сопоставляет положение пикселей изображений $|I\rangle$ и $|K\rangle$ с помощью h+w вентилей CNOT : если YX_I совпадают с YX_K , то далее пройдёт состояние $|0\rangle^{\otimes(h+w)}$ , так как CNOT(1,1)=CNOT(0,0)=0 .

В блоке 2 используется вспомогательный кубит $|A\rangle$ , который изменяется с $|0\rangle$ на $|1\rangle$ , если в предыдущем блоке YX_I=YX_K .

В блоке 3 применяется операция XOR с кубитами, отвечающими за цвет изображений $|I\rangle$ и $|K\rangle$ , в случае, если $|A\rangle=|1\rangle$ .

Для дешифрования используется эта же схема, при этом необходимо поменять местами исходное изображение $|I\rangle$ и зашифрованное изображение $|M\rangle$ .

Рис. 4. Схема XOR между двумя изображениями

В качестве примера на рисунке 5 показано шифрование изображения $2 \times 2$ , где цвет каждого пикселя принимает значения от 0 до 3.

На рисунке 6 показано изображение до и после применения описанного алгоритма шифрования. Так, зашифрованное изображение представляет собой случайный шум, в котором нельзя определить детали исходного изображения.

Рис. 6. (а) Исходное изображение. (b) Зашифрованное изображение.

В этом алгоритме размер ключа соответствует размеру изображения $H \times W$ умноженному на количество кубит для цвета . Пространство ключей размера $2^{qHW}$ достаточно велико, чтобы невозможно было за разумное время подобрать ключ шифрования. Об анализе с точки зрения статистики и анализе компьютерной сложности алгоритма можно прочитать в оригинальной статье [2].

Перейдем к обсуждению методов QIE на основе частотной области. В этом случае операции над изображением происходят после перехода в частотную область. Для этого в существующих алгоритмах применяется квантовое преобразования Фурье или квантовое вейвлет-преобразование. Рассмотрим подробнее пример алгоритма шифрования в частотной области.

Квантовое шифрование на основе квантового преобразования Фурье и двухфазного кодирования

В данном алгоритме для представления изображения используется модель FRQI (Flexible Representation of Quantum Images). Аналогично предыдущей модели, изображение состоит из двух частей: одна отвечает за цвет, другая — за положение пикселя:

$|c_{j}\rangle=\left(cos\theta_j|0\rangle+sin\theta_j|1\rangle\right)$ — кодирование цвета,

$|j\rangle=|y_{n-1} y_{n-2} \ldots y_{0}\rangle|x_{n-1} x_{n-2} \ldots x_{0}\rangle$ — кодирование положения пикселя,

где $x_i\ , y_i \in\{0,1\}, \theta_{j} \in[0,\ \pi/2]$ . $|1\rangle, |0\rangle$ — это двумерные базисные квантовые состояния. Строка $\left(\theta_{0}, \theta_{1}, \ldots, \theta_{2^{2 n}-1}\right)$ — вектор фаз, отвечающих за оттенок серого для каждого пикселя. Так, изображение $2^n \times 2^n$ в представлении модели FRQI выглядит следующим образом:

$|I\rangle=\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1}\left|c_{j}\right\rangle \otimes|j\rangle.$

Имеем исходное изображение — $|I\rangle$ , ключи для пространственной области и области квантового преобразования Фурье (англ. Quantum Fourier transform, QFT) — операции поворота фазы, применяющиеся к состояниям $|c_j\rangle$

$R_{K_{1}}=\begin{bmatrix} cos\ \psi_j & sin\ \psi_j \\ -sin\ \psi_j & cos\ \psi_j \end{bmatrix},\ \ \ R_{K_{2}}=\begin{bmatrix} cos\ \nu_j & sin\ \nu_j \\ -sin\ \nu_j & cos\ \nu_j \end{bmatrix}.$

Алгоритм шифрования выглядит следующим образом:

Шаг 1. Кодирование исходного изображения $|I\rangle$ в пространственной области c использованием ключа $|K\rangle$ для получения $|P_1\rangle$

Шаг 1.

$\begin{aligned} |P_1\rangle &=K_{1}|I\rangle=R_{K_{1}} \otimes I_{2^{2 n}}|I\rangle \\ &=\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1} R_{K_{1}}\left|c_{j}\right\rangle \otimes|j\rangle \\ &=\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1}\left|d_{j}\right\rangle \otimes|j\rangle, \end{aligned}$

где $|d_j\rangle = ( cos(\theta_j + \psi_j)|0\rangle + sin(\theta_j+\psi_j)|1\rangle).$

Шаг 2. Квантовое преобразование Фурье $QFT(|P_1\rangle)$

Шаг 2.

$Q F T(|P_1\rangle)=Q F T\left(\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1}\left|d_{j}\right\rangle \otimes|j\rangle\right).$

Здесь QFT в ортонормированном базисе $|0\rangle, \ldots, |N-1\rangle$ определяется как линейный оператор действующий следующим образом:

$Q F T:|j\rangle \rightarrow \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{2 \pi i j k / N}|k\rangle.$

Шаг 3. Кодирование $QFT(|P_1\rangle)$ в частотной области c использованием ключа K_2 для получения $|P_2\rangle$

Шаг 3.

$\begin{aligned} \left|P_{2}\right\rangle &=K_{2}\ Q F T(|P_1\rangle) \\ &=R_{K_{2}} \otimes I_{2^{2 n}}\ Q F T(|P_1\rangle) \\ &=R_{K_{2}} \otimes I_{2^{2 n}}\ Q F T\left(\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1}\left|d_{j}\right\rangle \otimes|j\rangle\right) \\ &=\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1} R_{K_{2}} Q F T\left(\left|d_{j}\right\rangle \otimes|j\rangle\right) . \end{aligned}$

Шаг 4. Применение обратного квантового преобразования Фурье $inQFT(|P_2\rangle)$ для получения окончательного зашифрованного изображения $|M\rangle$

Шаг 4.

$|M\rangle=\operatorname{in} Q F T\left(\frac{1}{2^{n}} \sum_{j=0}^{2^{2 n}-1} R_{K_{2}} Q F T\left(\left|d_{j}\right\rangle \otimes|j\rangle\right)\right).$

Рис. 6. Алгоритм шифрования с использованием QFT

Поскольку все преобразования, используемые в квантовых вычислениях, являются унитарными преобразованиями, процедура шифрования полностью обратима. Поэтому, для дешифрования необходимо проделать те же шаги в обратном порядке.

На рисунке 7 можем видеть исходное и зашифрованное с помощью описанного алгоритма изображение.

Рис. 7. (a) Исходное изображение. (b) Зашифрованное изображение.

Аналогично алгоритму шифрования с ключом-изображением в описанной криптосистеме пространство ключей такое же большое, как изображение открытого текста. Сами ключи при этом представляют собой две независимые последовательности в пространственной области и частотной области QFT, соответственно.

Хороший алгоритм шифрования изображений должен обладать высокой чувствительностью к ключу. Если злоумышленник использует ключ даже незначительно отличающийся от оригинального ключа, то при дешифровании полученное изображение не будет иметь ничего общего с исходным.

Для анализа чувствительности в статье [3] использовались следующие три пары ключей для дешифрования зашифрованного изображения: (a) правильные ключи пространственной и частотной области (b) правильный ключ частотной области с неправильным ключом пространственной области и (c) правильный ключ пространственной области с неправильным ключом частотной области. Результаты дешифрования показаны на рисунке 8.

Рис. 8. (a) Правильные ключи. (b) Неверный ключ пространственной области.
(с) Неверный ключ частотной области. — Рис. 8. (a) Правильные ключи. (b) Неверный ключ пространственной области. (с) Неверный ключ частотной области.

Видно, что в случае правильных ключей можно получить точное исходное изображение. С неправильным ключом пространственной области получается сильно зашумленное изображение, в котором еще можно видеть размытый контур исходного изображения. Наконец, используя неверный ключ частотной области расшифрованное изображение представляет собой случайный шум.

Заключение

В статье мы описали два основных на данный момент подхода к квантовому шифрованию изображений, а именно: с использованием преобразований в пространственной и в частотной области. Также чуть более подробно рассмотрели примеры квантовых алгоритмов шифрования, которые применялись к изображениям в оттенках серого. Чтобы работать с цветом, можно добавить ещё несколько кубитов, для кодирования красного, зеленого и синего каналов, при этом алгоритмы практически не изменятся. Так, расширение для метода шифрования цветных изображений с использованием квантового преобразования Фурье описано в работе [4].

На данный момент область QIP, в том числе квантовое шифрование изображений является быстро развивающейся областью, в которой используются возможности квантовой физики для расширения классических методов. Конечно, сейчас большинство исследований основано на моделировании квантовых алгоритмов, и чтобы подтвердить их эффективность, необходимо создание мощных и точных квантовых компьютеров. Так что пока остается лишь ждать развития квантовых технологий. Если вас заинтересовала эта тема, можно попытаться ускорить этот процесс попробовав себя в программировании квантовых алгоритмов с помощью qiskit [5], где присутствует раздел, посвящённый конкретно QIP.

Список используемых материалов

Yan, Fei & Iliyasu, Abdullah & Le, Phuc. (2017). Quantum image processing: A review of advances in its security technologies. International Journal of Quantum Information. 15. 1730001. 10.1142/S0219749917300017. (ResearchGate)
Wang, Jian & Geng, Ya-Cong & Han, Lei & Liu, Ji-Qiang. (2019). Quantum Image Encryption Algorithm Based on Quantum Key Image. International Journal of Theoretical Physics. 58. 10.1007/s10773-018-3932-y. (ResearchGate)
Yang, Yu-Guang & Xia, Juan & Jia, Xin & Zhang, Hua. (2013). Novel image encryption/decryption based on quantum Fourier transform and double phase encoding. Quantum Information Processing. 12. 10.1007/s11128-013-0612-y. (ResearchGate)
Yang, Yu-Guang & Jia, Xin & Sun, Si-Jia & Pan, Qing-Xiang. (2014). Quantum cryptographic algorithm for color images using quantum Fourier transform and double random-phase encoding. Information Sciences. 277. 445-457. 10.1016/j.ins.2014.02.124. (ResearchGate)
https://qiskit.org/textbook/ch-applications/image-processing-frqi-neqr.html#1.-The-FRQI-State

Комментарии (2)

Scratch
12.12.2021 15:02
#23812143
Почему нельзя по квантовому каналу передать симметричный ключ, а потом уже шифровать любым нормальным AESом с ключом 256 бит?
1. plus79501445397
  12.12.2021 16:41
  #23812369
  +2
  Насколько я понимаю, в статье приводятся алгоритмы прямого шифрования квантового состояния (которое содержится в кубитах, передается по квантовому каналу), а классические алгоритмы (AES и т.п.) оперируют с классической информацией (биты, байты и т.д.). Квантовое состояние до какой-то размерности можно переводить в классическое, шифровать/передавать/расшифровывать классическим образом и обратно переводить в квантовое, но с ростом размерности это будет становиться уже не эффективно (и даже невозможно) и/или с существенными потерями по сравнению с более-менее эффективными методами шифрования квантовой информации напрямую (речь не обязательно про алгоритмы из этой статьи). Все эти рассуждения конечно для случая, когда квантовые компьютеры станут достаточно совершенны.