Как создавать модели прогнозирования временных рядов с помощью Darts.

Привет, это KOTELOV. Перевели статью, которая показалась интересной.

Изменение климата, несомненно, является одной из самых серьезных проблем, с которыми сталкивается человечество, и эксперты считают его экзистенциальной угрозой для нашего вида. Согласно Шестому оценочному докладу Межправительственной группы экспертов по изменению климата (МГЭИК), увеличение частоты экстремальных погодных явлений связано с изменением климата, и для решения этой проблемы необходимо принять решительные меры во всем мире¹. В противном случае пострадают миллионы людей, качество их жизни в последующие годы значительно снизится.

Парниковые газы (ПГ), такие как двуокись углерода (CO2) и метан (CH4), задерживают тепло в атмосфере, тем самым сохраняя нашу планету теплой и дружественной для биологических видов. Несмотря на это, человеческая деятельность, такая как сжигание ископаемого топлива, приводит к выбросу огромного количества парниковых газов, что приводит к чрезмерному повышению средней глобальной температуры Земли². Поэтому переход к устойчивой глобальной экономике необходим, чтобы мы могли смягчить последствия изменения климата и обеспечить процветание нашего вида. В этой статье мы собираемся применить прогнозирование временных рядов для данных о концентрации CO2 в атмосфере, что даст нам возможность исследовать пересечение машинного обучения и изменения климата.

Библиотека Darts

Разработчики библиотеки Darts стремятся упростить анализ временных рядов и прогнозирование с помощью Python. Darts поддерживает различные подходы к прогнозированию, начиная от классических статистических моделей, таких как ARIMA и экспоненциальное сглаживание, и заканчивая новыми методами, основанными на машинном и глубоком обучении. Кроме того, Darts включает в себя различные функции, которые позволяют нам понять статистические свойства временных рядов, а также оценить точность моделей прогнозирования. Если вы хотите узнать больше о Darts, вы можете прочитать это подробное введение в библиотеку или обратиться к официальной документации по API. Библиотека дартс позволит нам создавать различные модели прогнозирования на основе набора данных CO2 в Мауна-Лоа. Кроме того, мы собираемся сравнить точность этих моделей и использовать лучшую из них для прогнозирования значений концентрации CO2 в атмосфере на 2022 год.

Набор данных CO2 Мауна-Лоа

Вулкан Мауна-Луа является домом для одноименной обсерватории Мауна-Лоа (MLO), исследовательского центра, который занимается мониторингом атмосферы с 1950 года, а его удаленное расположение обеспечивает идеальные условия для записи климатических данных. В 1958 году Чарльз Дэвид Килинг учредил программу мониторинга CO2 MLO и начал регистрировать научные данные о быстром увеличении концентрации CO2 в атмосфере³. Набор данных CO2 в Мауна-Лоа был загружен из Океанографического института Скриппса и включает ежемесячные значения концентрации CO2 в атмосфере в частях на миллион (ppm) с 1958 по 2021⁴. Кроме того, набор данных также содержит сезонно скорректированные и сглаженные версии данных, но наш анализ будет сосредоточен исключительно на стандартных временных рядах.

Анализ временных рядов

В этом разделе мы собираемся извлечь некоторые сведения о наборе данных и его статистических свойствах. Это будет достигнуто с помощью различных типов графиков и других методов анализа временных рядов.

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from darts import TimeSeries
from darts.models import *
from darts.metrics import *
from darts.dataprocessing.transformers import Scaler
import logging

mpl.rcParams['figure.dpi'] = 300
logging.disable(logging.CRITICAL)

Начнем с импорта необходимых для нашего проекта библиотек Python, включая pandas, Matplotlib, а также различные функции из библиотек statsmodels и darts. После этого мы устанавливаем DPI рисунка Matplotlib на 300, поэтому мы получаем графики с высоким разрешением для этой статьи, но это необязательно.

df = pd.read_csv('data/monthly_in_situ_co2_mlo.csv',
                  comment = '"', header = [0,1,2], na_values = '-99.99')

cols = [' '.join(col).replace(' ', '') for col in df.columns.values]
df.set_axis(cols, axis = 1, inplace = True)

# Converting Excel date format to datetime
# and setting as dataframe index
df['datetime'] = pd.to_datetime(df['DateExcel'], origin = '1899-12-30', unit = 'D')

df.set_index('datetime', inplace = True)

df = df[['CO2filled[ppm]']]
df.rename(columns = {'CO2filled[ppm]': 'CO2'}, inplace = True)
df.dropna(inplace = True)
df = df.resample('M').sum()

После импорта библиотек мы продолжаем загружать набор данных в кадр данных pandas. Затем мы применяем к нему некоторые методы предварительной обработки данных, такие как удаление ненужных столбцов, установка ежемесячного индекса даты и времени и удаление нулевых значений.

df.plot(figsize=(8,5))
plt.title('Monthly CO2 Concentration (ppm)')

plt.show()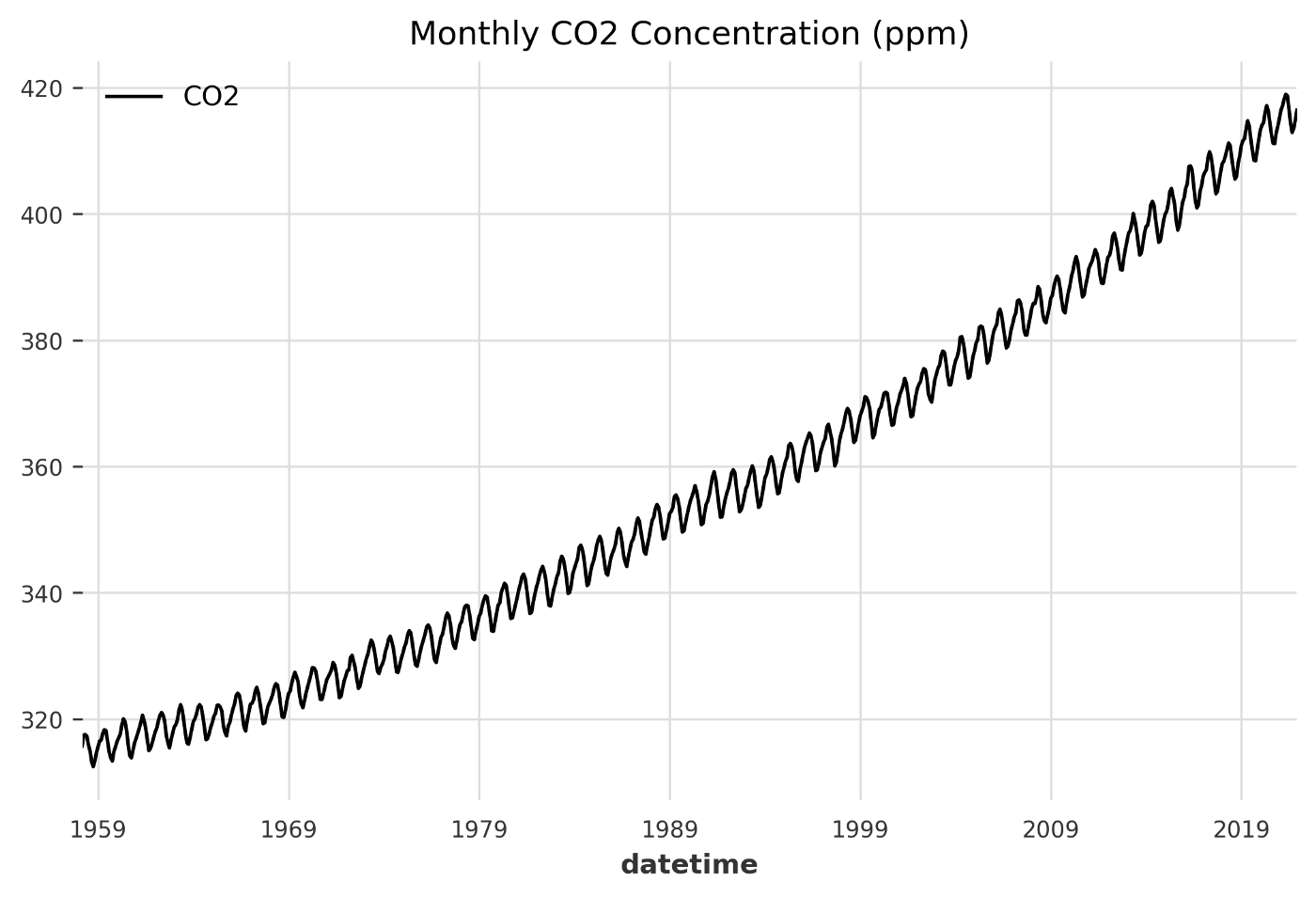

После очистки набора данных мы используем функцию pandas plot() для создания простого линейного графика временного ряда. Очевидно, существует четкая восходящая тенденция, подчеркивающая тот факт, что концентрация CO2 в атмосфере быстро увеличивалась в последние десятилетия. Кроме того, существует также сезонность из-за естественного углеродного цикла планеты, поскольку растения улавливают и выделяют CO2 в разные сезоны года⁵. В частности, когда растения начинают расти весной, они удаляют CO2 из атмосферы путем фотосинтеза. Напротив, когда лиственные деревья теряют листья осенью, CO2 высвобождается из-за дыхания.

mpl.rcParams['figure.figsize'] = (8, 6)

result = seasonal_decompose(df)
result.plot()

plt.show()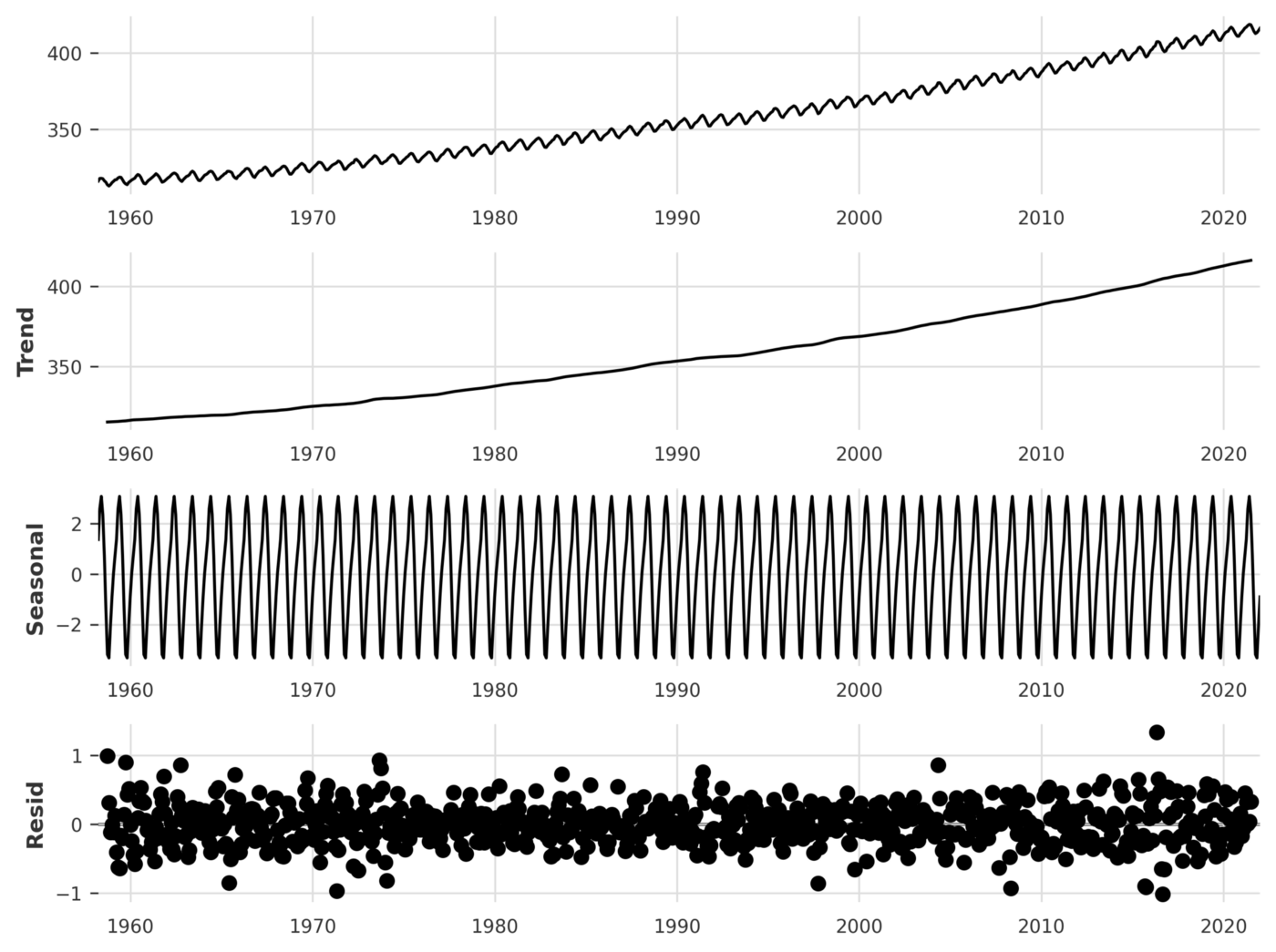

Мы используем функцию statsmodels Season_decompose(), чтобы применить декомпозицию к временному ряду, т.е. извлечь компоненты тренда, сезонности и остатков. После этого мы наносим эти компоненты на график и лучше понимаем тенденцию и сезонность, о которых упоминалось ранее. В этом конкретном случае мы уже могли идентифицировать компоненты, визуально рассматривая линейный график, но сезонная декомпозиция значительно помогает в более сложных случаях.

fig, ax = plt.subplots(figsize = (8,5))

plot_acf(df, ax = ax)

plt.show()

Мы используем функцию statsmodels plot_acf() для построения автокорреляционной функции (ACF) временного ряда, т. е. линейной зависимости между ее значениями с запаздыванием. Из-за тренда временного ряда мы можем видеть, что автокорреляция высока для небольших лагов и начинает постепенно уменьшаться после лага 5. АКФ также должна выделять сезонную составляющую временного ряда, но в данном случае она неразличима.

Прогнозирование временных рядов

В этом разделе мы собираемся обучить различные модели прогнозирования на наборе данных CO2 и сравнить их эффективность. После этого мы выберем наиболее точную модель и создадим на ее основе прогноз на 2022 год.

series = TimeSeries.from_dataframe(df)

start = pd.Timestamp('123115')
df_metrics = pd.DataFrame()

def plot_backtest(series, forecast, model_name):
    idx = -144
    series[idx:].plot(label='Actual Values')
    forecast[idx:].plot(label= 'Forecast')
    plt.title(model_name)
    plt.show()
    
def print_metrics(series, forecast, model_name):
    mae_ = mae(series, forecast)
    rmse_ = rmse(series, forecast)
    mape_ = mape(series, forecast)
    smape_ = smape(series, forecast)
    r2_score_ = r2_score(series, forecast)
    
    dict_ = {'MAE': mae_, 'RMSE': rmse_,
             'MAPE': mape_, 'SMAPE': smape_, 
             'R2': r2_score_}
    
    df = pd.DataFrame(dict_, index = [model_name])
    
    return(df.round(decimals = 2))  

Мы начинаем с загрузки фрейма данных pandas в объект TimeSeries, как того требует библиотека Darts. После этого мы создаем служебные функции plot_backtest() и print_metrics(), которые позволят нам строить прогнозы и отображать различные показатели модели, включая MAE, RMSE, MAPE, SMAPE и R².

Создание наивной модели прогнозирования

Установка базовой точности является стандартной практикой, поэтому мы собираемся сделать это, создав наивную модель. Это поможет нам оценить производительность более сложных моделей, которые теоретически должны иметь более высокую точность по сравнению с базовой линией. В этом случае мы собираемся создать наивную сезонную модель, которая всегда предсказывает значение на K шагов назад, где K равно сезонному периоду.

model = NaiveSeasonal(K = 12)
model_name = 'Naive Seasonal'

plt.figure(figsize = (8, 5))

forecast = model.historical_forecasts(series, start=start, forecast_horizon=12, verbose=True)
plot_backtest(series, forecast, model_name)
df_naive = print_metrics(series, forecast, model_name)
df_metrics = df_metrics.append(df_naive)

plt.show()
df_naive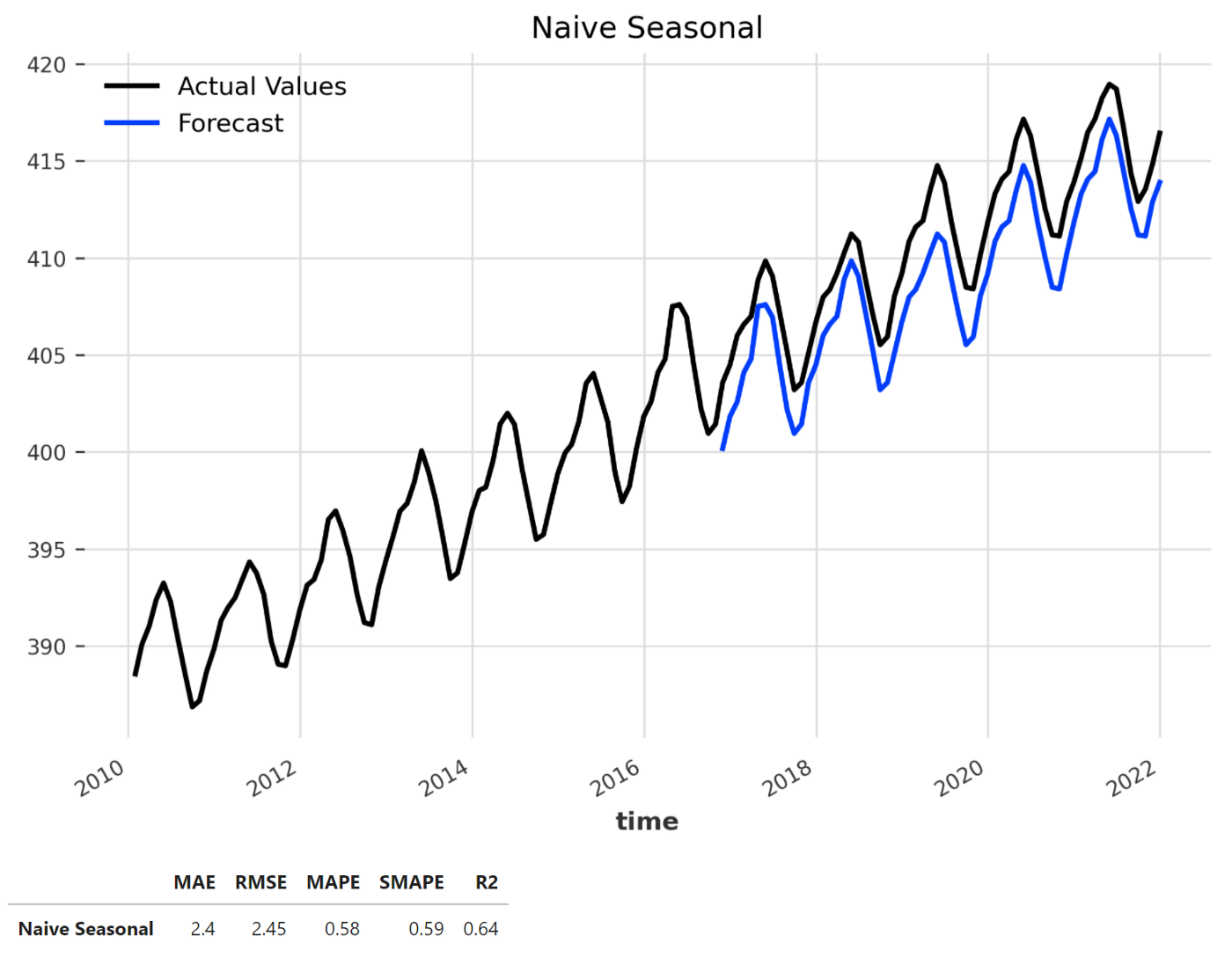

Чтобы протестировать наивную сезонную модель, мы используем функцию history_forecasts() с горизонтом прогноза 12 месяцев. Эта функция последовательно обучает модель в расширяющемся окне и по умолчанию сохраняет последнее значение каждого прогноза. Этот метод известен как ретроспективное тестирование или перекрестная проверка временных рядов, и он является более сложным по сравнению с типичным методом обучения/тестирования. После создания прогноза мы отображаем график и показатели с помощью функций полезности. Как мы видим, наивная сезонная модель работала достаточно хорошо, со значением SMAPE 0,59%.

Создание модели прогнозирования экспоненциального сглаживания

Теперь, когда мы установили базовую точность, мы собираемся создать модель прогнозирования на основе экспоненциального сглаживания Холта-Винтера, классического подхода, который успешно используется с 1960-х годов⁶.

model = ExponentialSmoothing(seasonal_periods = 12)
model_name = 'Exponential Smoothing'

plt.figure(figsize = (8, 5))

forecast = model.historical_forecasts(series, start=start, forecast_horizon=12, verbose=True)
plot_backtest(series, forecast, model_name)
df_exp = print_metrics(series, forecast, model_name)
df_metrics = df_metrics.append(df_exp)

plt.show()
df_exp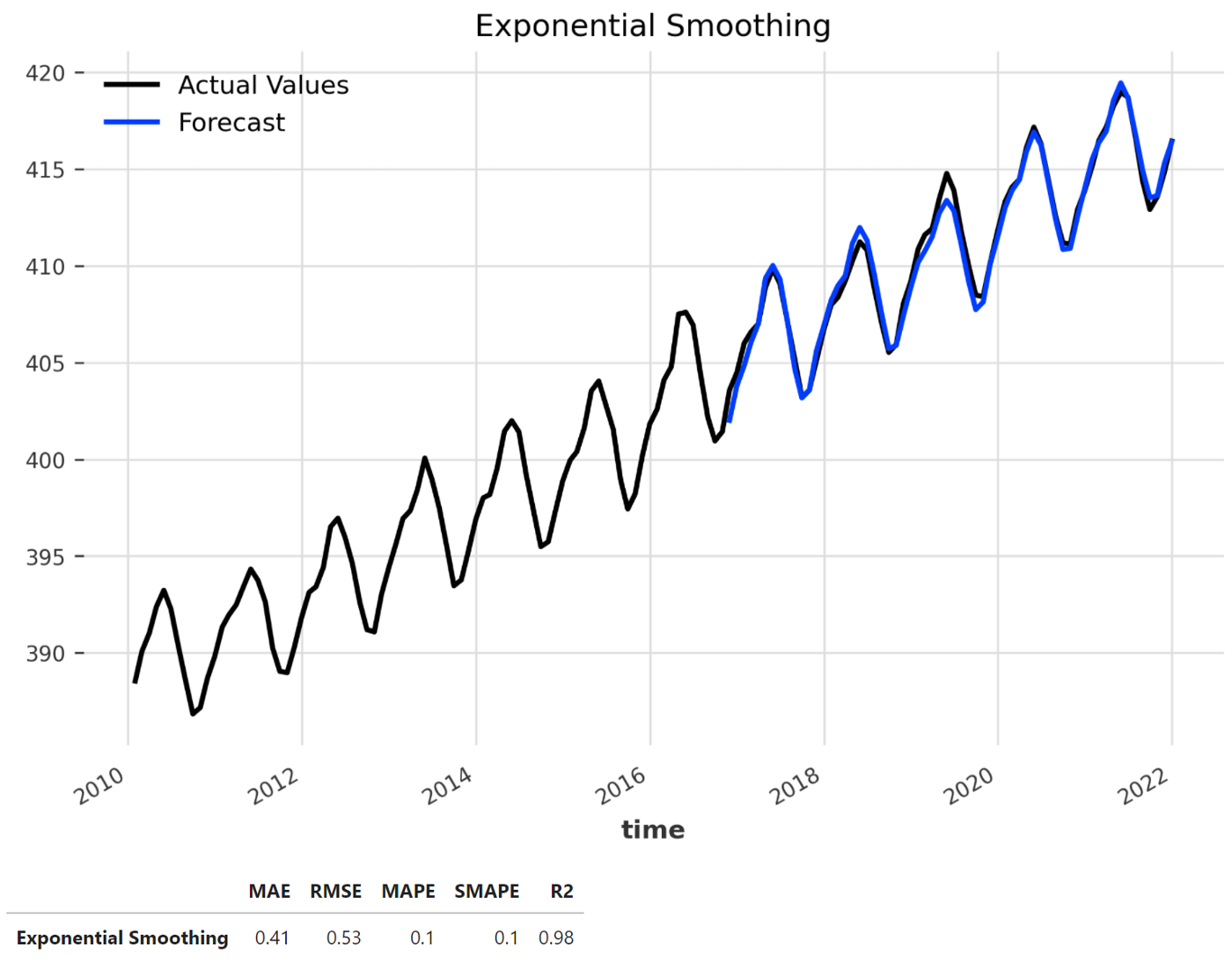

Как и ранее, мы используем функцию history_forecasts(), а также вспомогательные функции для оценки производительности модели. Очевидно, что модель экспоненциального сглаживания значительно превосходит наивную модель со значением SMAPE, равным 0,1%. Мы также можем визуально подтвердить это, заметив, что прогнозируемые значения почти идентичны значениям набора данных, нанесенным на график.

Создание модели прогнозирования линейной регрессии

В последние годы модели машинного обучения широко использовались при прогнозировании временных рядов в качестве альтернативы классическим подходам. Просто добавляя запаздывающие значения в качестве признаков в набор данных, мы можем превратить прогнозирование временных рядов в задачу регрессии⁷. Поэтому мы можем использовать любую регрессионную модель scikit-learn или другие библиотеки с совместимым API, включая XGBoost и LightGBM. В этом случае мы собираемся создать модель линейной регрессии на основе библиотеки scikit-learn.

model = LinearRegressionModel(lags = 12)
model_name = 'Linear Regression'

plt.figure(figsize = (8, 5))

forecast = model.historical_forecasts(series, start=start, forecast_horizon=12, verbose=True)
plot_backtest(series, forecast, model_name)
df_lr = print_metrics(series, forecast, model_name)
df_metrics = df_metrics.append(df_lr)

plt.show()
df_lr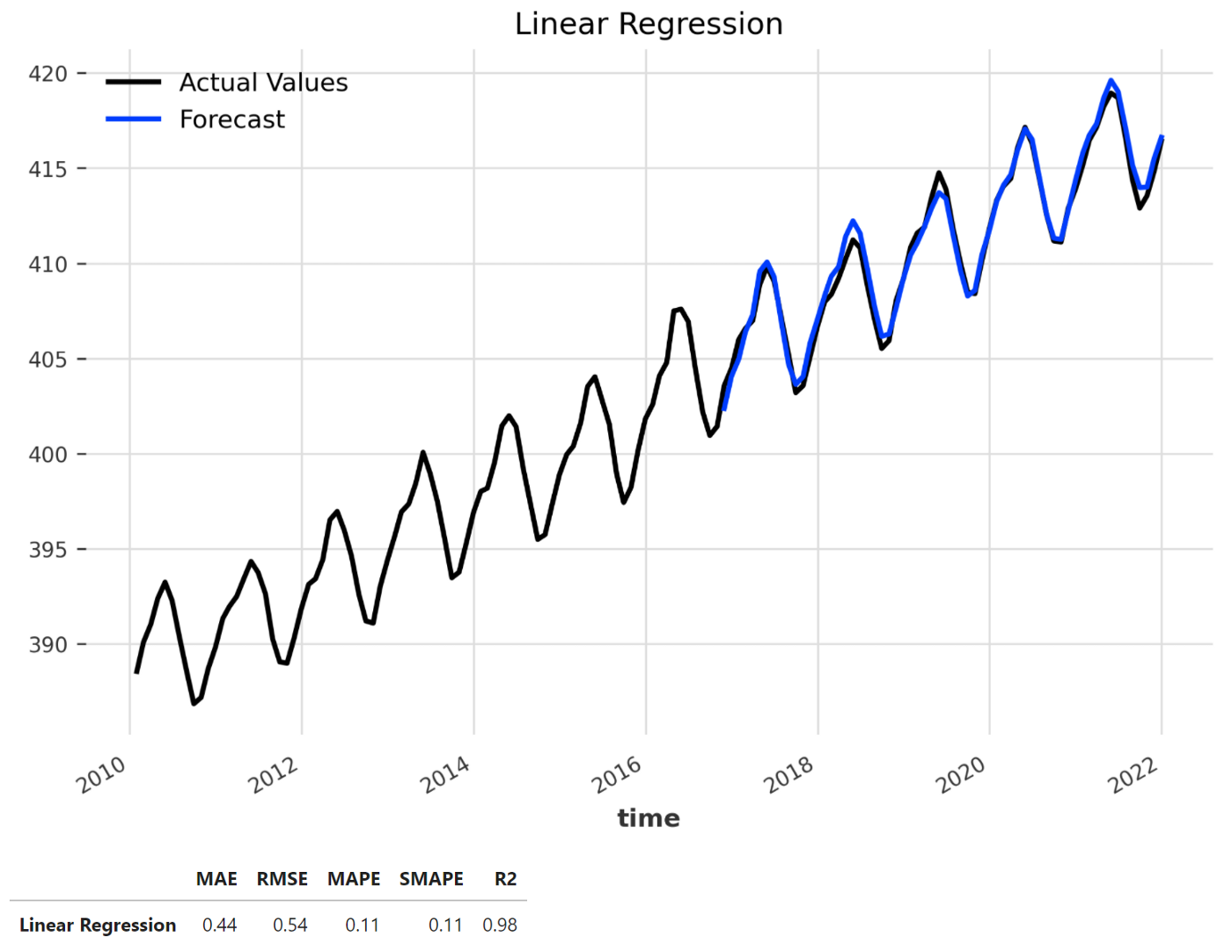

Используя history_forecasts() и служебные функции, мы тестируем модель линейной регрессии и впоследствии отображаем результаты. Как мы видим, модель имеет отличную производительность со значением SMAPE 0,11%.

Создание модели прогнозирования временной сверточной сети

В последние годы глубокое обучение стало популярным в прогнозировании временных рядов, при этом рекуррентные нейронные сети стали стандартным выбором в исследованиях, а также в практических приложениях. Несмотря на это, временная сверточная сеть — это альтернативная архитектура, дающая многообещающие результаты⁸, поэтому мы собираемся проверить ее производительность.

model = TCNModel(
    input_chunk_length=24,
    output_chunk_length=12,
    n_epochs=100,
    dropout=0.1,
    dilation_base=3,
    weight_norm=True,
    kernel_size=5,
    num_filters=3,
    random_state=0,
)

model_name = 'TCN'

plt.figure(figsize = (8, 5))

scaler = Scaler()
scaled_series = scaler.fit_transform(series)
forecast = model.historical_forecasts(scaled_series, start=start,
                                      forecast_horizon=12, verbose=True)
plot_backtest(series, scaler.inverse_transform(forecast), model_name)
df_dl = print_metrics(series, scaler.inverse_transform(forecast), model_name)
df_metrics = df_metrics.append(df_dl)

plt.show()
df_dl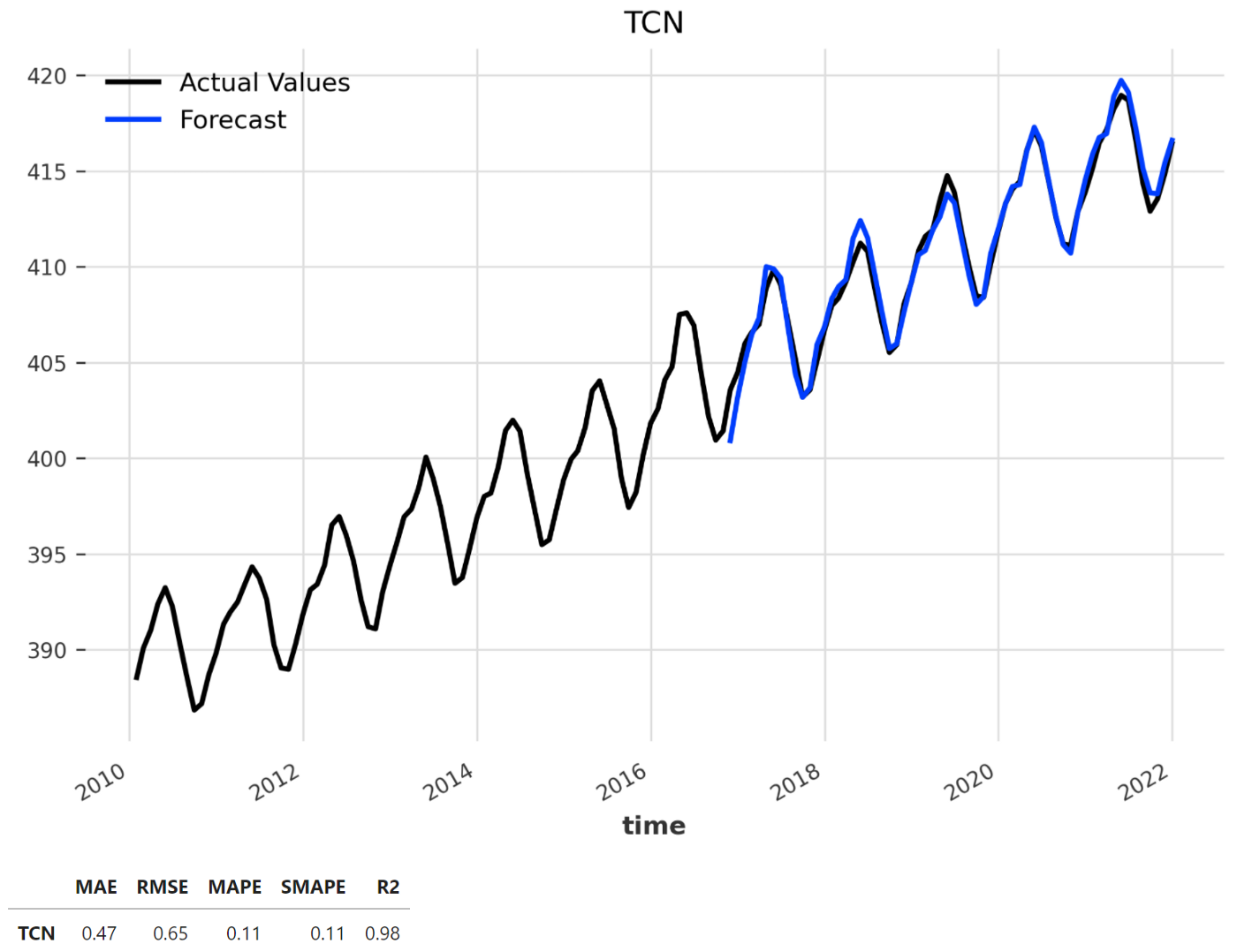

Как и ранее, мы используем history_forecasts() и служебные функции для тестирования модели временной сверточной сети и отображения результатов. Кроме того, мы также нормализуем временные ряды с помощью класса Scaler(). Очевидно, что модель TCN имеет значительно лучшую производительность по сравнению с базовой линией со значением SMAPE, равным 0,11%.

Создание прогноза

Как и ожидалось, все модели превзошли наивную сезонную модель, обеспечив превосходную точность. Несмотря на это, мы видим, что экспоненциальное сглаживание обеспечивает наилучшие результаты, поэтому наш прогноз концентрации CO2 в атмосфере на 2022 год будет основан на нем.

model = ExponentialSmoothing(seasonal_periods = 12)
model_name = 'Exponential Smoothing'

model.fit(series)
forecast = model.predict(12)

plot_backtest(series, forecast, model_name)
print(forecast.pd_dataframe())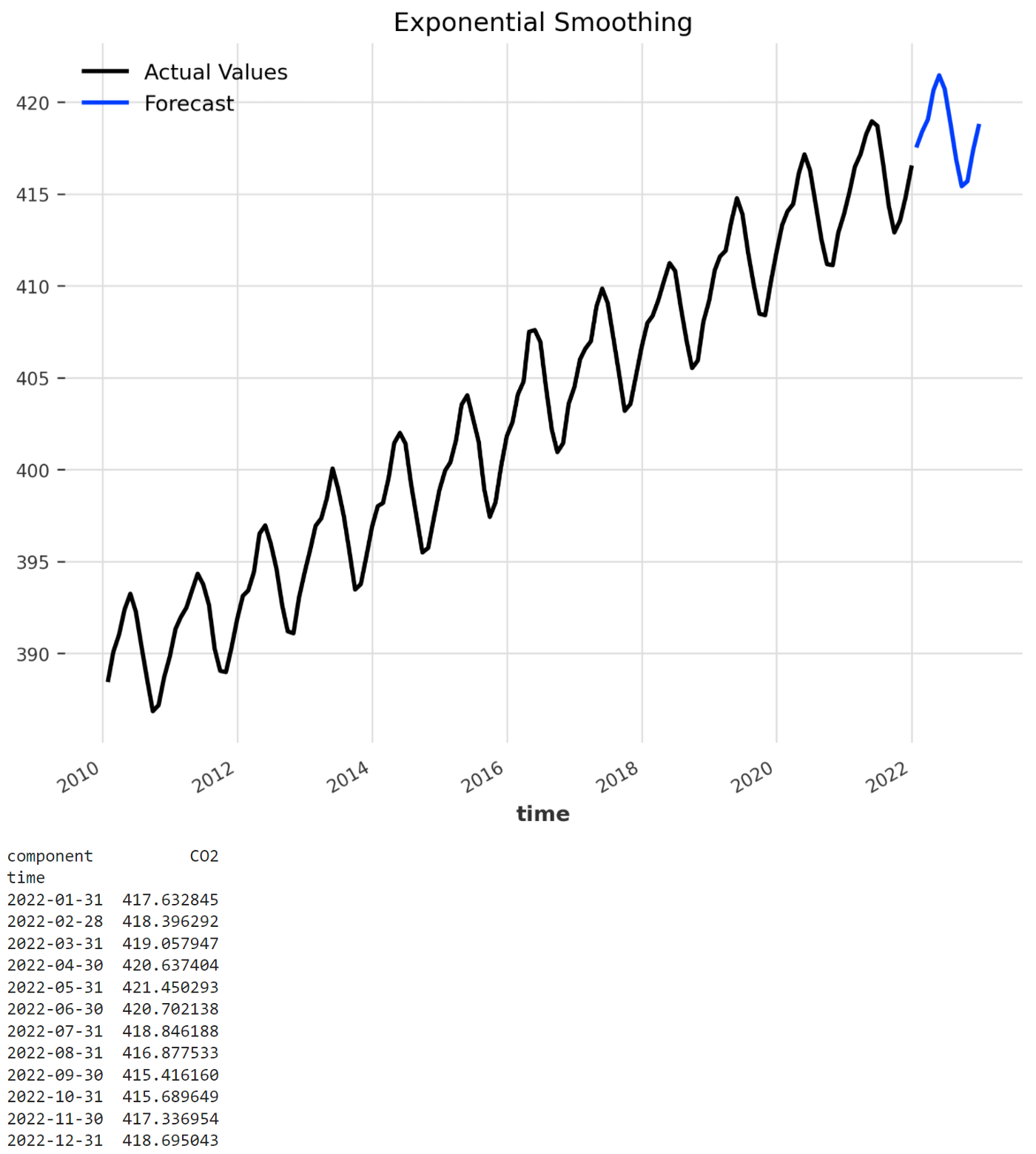

Мы используем функцию fit(), чтобы подогнать модель экспоненциального сглаживания ко всему набору данных, а затем отобразить результаты. Как мы можем визуально наблюдать, компоненты временного ряда были успешно идентифицированы моделью. Кроме того, мы можем сравнить наш результат с официальным прогнозом CO2 Метеорологического бюро Соединенного Королевства (Метеорологического бюро) на 2022 год. Как и ожидалось, два прогноза имеют почти одинаковые значения, что подтверждает точность модели экспоненциального сглаживания. Может показаться удивительным, что экспоненциальное сглаживание дало наилучшие результаты вместо моделей машинного обучения и глубокого обучения. Несмотря на это, мы должны иметь в виду, что новые модели не обязательно лучше в каждом случае по сравнению с классическими методами. Кроме того, модели машинного обучения можно оптимизировать, применяя настройку гиперпараметров — технику, которая отнимает много времени и является сложной, но может предложить значительные улучшения.

Заключение

В этой статье мы рассмотрели один из способов использования науки о данных для борьбы с изменением климата — процветающей и разнообразной области исследований, которая постоянно растет⁹, поэтому я призываю вас узнать о ней больше. К сожалению, мы также обнаружили, что в этом году ожидается увеличение концентрации CO2 в атмосфере, что подчеркивает тот факт, что выбросы должны быть сокращены, чтобы обеспечить процветание нашего вида. Наконец, код и данные этой статьи доступны в этом репозитории Github, так что не стесняйтесь клонировать их. Я также призываю вас делиться своими мыслями в комментариях или подписываться на меня в LinkedIn, где я регулярно публикую материалы о науке о данных, изменении климата и других темах. Вы также можете посетить мой личный веб-сайт или прочитать мою последнюю книгу под названием «Упрощение машинного обучения с помощью PyCaret».

Список литературы:

[1] Чжай П. и др. «IPCC 2021: Изменение климата 2021: Физическая научная основа. Вклад Рабочей группы I в шестой оценочный отчет Межправительственной группы экспертов по изменению климата». (2021).

[2] Хоутон, Джон. "Глобальное потепление." Отчеты о прогрессе в физике 68.6 (2005): 1343.

[3] Харрис, Дэниел К. «Чарльз Дэвид Килинг и история измерений CO2 в атмосфере». Аналитическая химия 82.19 (2010): 7865–7870.

[4] Килинг, Чарльз Д. и др. «Обмен атмосферным СО2 и 13СО2 с земной биосферой и океанами с 1978 по 2000 гг. I. Глобальные аспекты». (2001).

[5] Килинг, Чарльз Д. «Концентрация и содержание изотопов углекислого газа в атмосфере в сельской местности». Geochimica et космохимика acta 13.4 (1958): 322-334.

[6] Уинтерс, Питер Р. «Прогнозирование продаж с помощью экспоненциально взвешенных скользящих средних». Наука управления 6.3 (1960): 324–342.

[7] Диттерих, Томас Г. «Машинное обучение для последовательных данных: обзор». Совместные международные семинары IAPR по статистическим методам распознавания образов (SPR) и структурно-синтаксического распознавания образов (SSPR). Спрингер, Берлин, Гейдельберг, 2002.

[8] Бай, Шаоцзе, Дж. Зико Колтер и Владлен Колтун. «Эмпирическая оценка общих сверточных и рекуррентных сетей для моделирования последовательности». Препринт arXiv arXiv: 1803.01271 (2018).

[9] Ролник, Дэвид и др. «Борьба с изменением климата с помощью машинного обучения». Вычислительные исследования ACM (CSUR) 55.2 (2022): 1–96.