В мире полно вопросов на которые нет четкого ответа: есть ли жизнь после смерти, одни ли мы во Вселенной, для чего козе баян? Последний вопрос хоть и является поговоркой, не имеющей реального подтверждения факта использования козой музыкального инструмента, однако косвенно затрагивает тему сегодняшнего исследования. Многие вещи, явления и процессы мы связываем либо с миром дикой природы, либо с миром людей. Наш развитый интеллект позволил нам многое создать и многое изучить. Науки, особенно точные, мы считаем прерогативой ума человеческого, а не животного, занятого лишь мыслями о еде, размножении и выживании. Хотя и мы сами, порой того не осознавая, занимаемся тем же, просто в более техногенной обертке. Что касается мыслительных процессов, то умение прибавлять/вычитать в пределах от 1 до 5 для человека не является подспорьем для получения Нобелевской по математике. Но вот для представителей дикой природы — это удивительный навык. Особенно, если речь идет о рыбах. Ученые из Боннского университета (Германия) провели любопытные опыты, результаты которых показали наличие у скатов и цихлид базовых арифметических навыков. Насколько хороши рыбы в счете, как именно ученые смогли это проверить, и о чем говорят результаты наблюдений? Ответы на эти вопросы мы найдем в докладе ученых. Поехали.

Основа исследования

На самом деле, умение различать количество не является уникальной способностью человека. Многие позвоночные и даже некоторые виды беспозвоночных также это умеют. И логика в этом достаточно проста, так как количественное распознавание (включая численное распознавание) жизненно важно для многих видов в контексте повседневной деятельности, такой как поиск пищи, избегание хищников, обучение в стае и выбор партнера.

Количественное распознавание может быть основано на нескольких параметрах, таких как непрерывные (например, размер или площадь поверхности, покрываемая предметами) или дискретные переменные (количество предметов). Хотя обе стратегии не являются взаимоисключающими и могут в сочетании друг с другом давать более успешный результат, некоторые виды используют только непрерывные переменные, чтобы основывать свой выбор на них.

В нескольких исследованиях было высказано предположение, что существуют две разные системы численного дифференцирования (т.е. численного распознавания). Большинство исследований рыб поддерживают гипотезу применения обеих систем.

С помощью первой из двух предполагаемых систем, «объектной системы файлов» (OFS от object file system), небольшие объемы, отличающиеся только одним элементом, могут быть точно записаны. Однако верхний предел низкий и колеблется от 3 до 5 пунктов для большинства особей. Другими словами, многие особи способны различать число предметов на 1 в пределах 5. Для OFS числовое соотношение не имеет значения; вместо этого важна общая композиция изображения или количество элементов, хранящихся в рабочей памяти.

С помощью второй системы числового распознавания, «системы аналоговых величин» (AMS от analogue magnitude system), можно приблизительно оценить и сравнить большие числовые значения. Точность различия размеров подчиняется закону Вебера и зависит от соотношения между двумя различаемыми величинами. Распознавание более успешно при увеличении соотношения между двумя числовыми выборками.

Чтобы изучить эти две предложенные системы и их ограничения, были проведены исследования на различных организмах (приматы, саламандры, пересмешники, большеклювые вороны, трёхиглые колюшки, гуппи, гамбрузии Хольбрука и т.д.). Большинство этих исследований установили верхние пределы для OFS около 3–5, при этом различие между элементами 3: 4 или 4: 5 больше не было успешным. Но вот гуппи могли отличить 4 от 5, а колюшки могли увидеть разницу даже между 6 и 7.

Недавно было установлено, что у скатов вида Potamotrygon motoro и акул вида Chiloscyllium griseum OFS равно 4. При этом 4:3 и 5:3 распознаются успешно, а вот 4:5 – нет. У цихлид OFS колеблется от 1 до 5, при этом 4:5 по-прежнему успешно распознается большинством особей.

Вышеописанные наблюдения действительно интересны, но пока не было никаких точных данных касательно умения позвоночных, помимо людей и приматов, успешно решать числовые или арифметические задачи, такие как сложение и вычитание. Ранее подобные навыки изучались только у приматов, птиц, пауков и даже пчел.

В недавнем исследовании (Numerical cognition in honeybees enables addition and subtraction) медоносные пчелы распознавали цвета как символы для выполнения задач на сложение и вычитание. Пчелы успешно складывали и вычитали объекты и применяли эти знания в тестах на передачу неизвестного количества объектов, что свидетельствует о приобретении долговременных правил и кратковременной рабочей памяти. Пчел учили летать в Y-образную комнату для образцов, в которой им первоначально предъявляли один визуальный «тестовый» стимул (синий или желтый), отображающий определенное количество геометрических объектов. Затем они должны были пролететь через отверстие в камеру принятия решений и выбрать один из двух стимулов выбора (стимулы А и В). Они содержали на один элемент больше (стимул A) и на один элемент меньше (стимул B), чем тестовый стимул, показанный ранее. В зависимости от цвета тестового стимула пчелы успешно выполняли сложения и вычитания в числовом пространстве от 1 до 5.

Авторы рассматриваемого нами сегодня труда решили использовать опыт, проведенный с пчелами, и применить его для оценки арифметических навыков цихлид и пресноводных скатов. Именно эти рыбы были выбраны для опытов, так как предыдущие исследования показали, что и цихлиды, и скаты хорошо подходят для когнитивных экспериментов, демонстрируя широкий спектр когнитивных способностей, от экспериментов по визуальному различению до пространственной ориентации.

Подготовка к опытам

Pseudotropheus zebra (слева) и Potamotrygon motoro (справа).

В экспериментах приняли участие 8 цихлид (Pseudotropheus zebra) и 8 пресноводных скатов (Potamotrygon motoro). Шесть цихлид ранее участвовали в когнитивных экспериментах, двое других были экспериментально «чистыми».


Изображение №1

Для обоих видов жилые резервуары также служили экспериментальными резервуарами. Цихлид содержали индивидуально в испытательных аквариумах размером 61х31х31 см с максимальным объемом 54 л (схема выше). Отдельные баки были разделены пополам серой непрозрачной перегородкой на передний и задний отсеки. Рыба могла проплыть через окно размером 7х7 см (управляемое вручную прозрачной подъемной дверцей) в перегородке, чтобы использовать обе области. Пол жилого отсека (стартовый отсек) был засыпан песком, в то время как в переднем отсеке (опытный отсек) он был пуст.

С помощью проектора (Optima) слайды в формате Power Point демонстрировались на стенке с двухмерными геометрическими символами в качестве стимулов. С помощью пипеток, прикрепленных к длинной трубке, одна пищевая гранула выбрасывалась сразу после того, как был сделан правильный выбор. За ходом всех опытов ученые наблюдали с помощью камеры Logitec.


Изображение №2

Всех скатов содержали вместе в одном резервуаре (1300 л) размерами 2.30х2.07х0.40 м, в котором также находилась экспериментальная установка (схема выше). Экспериментальная установка (53.5х106 см) состояла из стартового отсека, переходной зоны и зоны принятия решений, разделенных двумя дверками с ручным управлением. Стимулы демонстрировались с помощью ламинированных карточек (А4) на передней стороне резервуара, который был разделен пластиковой перегородкой на две зоны принятия решений. После правильного выбора пища (дождевые черви, креветки) подавалась с помощью щипцов. За скатами также наблюдали с помощью камеры Logitec.

Сначала, еще находясь в стартовом отсеке, цихлидам предъявляли исходный тестовый стимул в течение пяти секунд на передней части аквариума молочного цвета. Цихлиды наблюдали этот раздражитель через закрытую, но прозрачную дверку. Через пять секунд представление стимула менялось на стимулы с двумя вариантами выбора, и дверь открывалась. Как только испытуемая особь переплывала двери, начинался отсчет времени. В тот момент, когда рыба пересекала линию принятия решения, время останавливалось и записывался выбор. Если особь делала правильный выбор, ее награждали, если выбор был неверным, проекцию останавливали и вместо нее показывали черный слайд. Затем испытуемый возвращался в стартовый отсек, а дверки закрывались.

В опытах со скатами первая дверка была поднята, а испытуемым был предъявлен исходный тестовый стимул в течение пяти секунд. Затем была поднята вторая дверь, и скаты могли войти в экспериментальную зону и зону принятия решений, где два стимула выбора предъявлялись на ламинированных карточках по обе стороны от перегородки. Как только скат проплывал через вторые двери, начинался отсчет времени. В тот момент, когда скат пересекал линию принятия решения, запись времени останавливалась. Если скат делал правильный выбор, его награждали, если выбор был неверным, карточки убирали.


Изображение №3

В ходе наблюдений было реализовано три типа экспериментов (A, B и C).

Эксперимент A: тестовых стимулов — 3; сложение (синий) — 4 (правильный выбор) или 2 (неправильный выбор); вычитание (желтый) — 2 (правильный выбор) или 4 (неправильный выбор).

В этом тесте ранее неиспользованное количество из трех символов предъявлялось в качестве тестового стимула (чтобы исключить запоминание символов), и затем рыба должна была выбирать между 2 и 4 символами. Этот тест был выполнен с использованием обоих цветов. Когда были представлены синие символы, ожидалось, что рыба выберет объект с более высоким номером, т. е. добавит «единицу». А для желтых символом рыба должна была вычесть «единицу».

Эксперимент B: тестовых стимулов — 3; сложение (синий) — 4 (правильный выбор) или 5 (неправильный выбор); вычитание (желтый) — 2 (правильный выбор) или 1 (неправильный выбор).

Этот тест определял, научилась ли рыба выбирать стимул с наибольшим или наименьшим количеством объектов в зависимости от представленного цвета, или же рыба действительно научилась прибавлять или вычитать «единицу» из тестового стимула. Стимулы выбора в этом тесте включали либо плюс один и плюс два (синий), либо минус один и минус два (желтый).

Эксперимент C: тестовых стимулов — 3; сложение (синий) — скорректированный размер стимулов 4 (правильный выбор) или 2 (неправильный выбор); вычитание (желтый) — скорректированный размер стимулов 2 (правильный выбор) или 4 (неправильный выбор).

Этот тест переноса контролировал влияние единственного потенциально искажающего фактора, т. е. размера отдельного символа. В то время как форма поверхности, расположение и площадь, покрытая стимулами, контролировались на многих экспериментальных стимульных карточках/проекциях, размер отдельных символов контролировался в меньшей степени (лишь на некоторых карточках). Это привело к тому, что отдельные символы в большинстве случаев были больше для меньших чисел и меньше для больших чисел. Чтобы контролировать это смещение, соотношение было изменено на противоположное: отдельные символы для меньшего варианта теперь были меньше, а символы для большего варианта теперь были больше.

Результаты экспериментов

Цихлиды

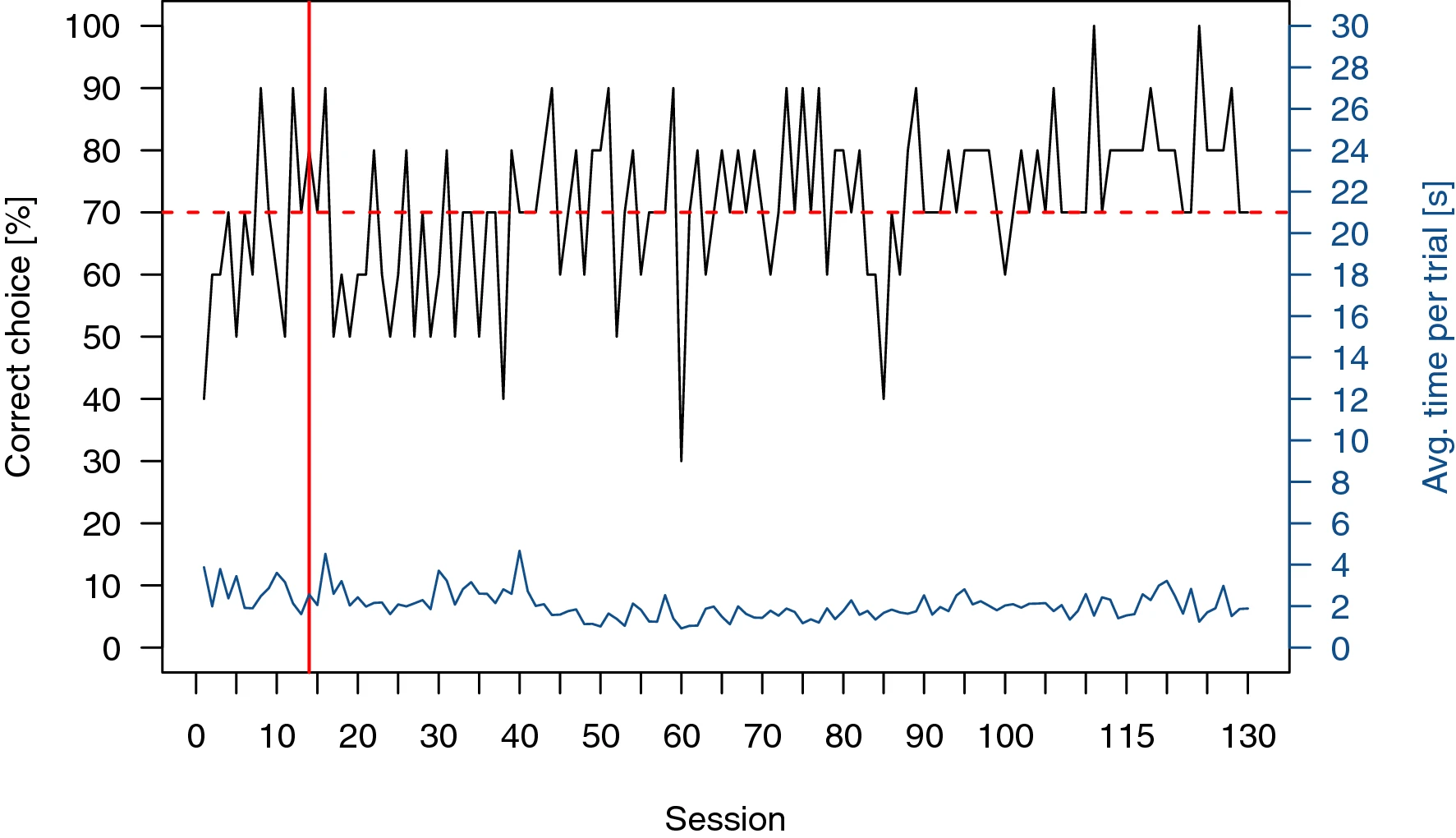
Изображение №4

Все шесть особей, участвовавших в тренинге, достигли нужного уровня обучения в среднем за 28 ± 18 сессий и участвовали во всех последующих тестах. Примерный график продуктивности одной цихлиды за все время эксперимента показан выше.

Во время тестов A, B и C индивидуальные выборы, объединенные в группу, показали, что цихлиды значительно чаще выбирали правильный стимул (+1/−1). В задаче на сложение теста А испытуемые были верны в 117 из 141 случаях (n = 6, p < 0.0001) и в 96 из 141 раза (n = 6, p < 0.01) в задаче на вычитание (5а).


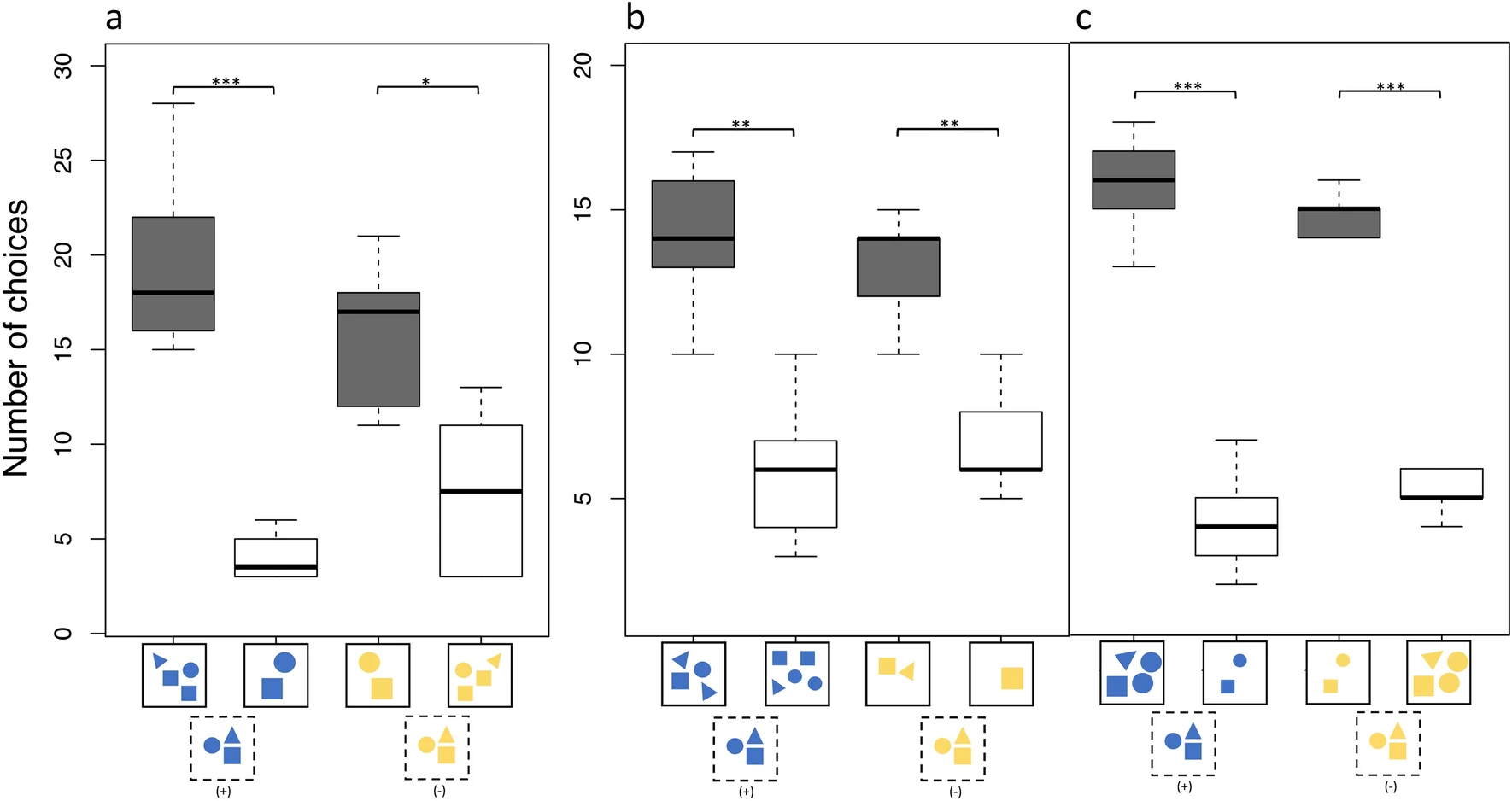
Изображение №5

В тесте B особи были верны 84 из 120 раз в задаче на сложение (n = 6, p < 0.001) и 79 из 120 раз (n = 6, p < 0.001) в задаче на вычитание (5b). Выборы в задаче на сложение в тесте С были правильными в 95 случаях из 120 (n = 6, p < 0.0001) и в 89 из 120 раз (n = 6, p < 0.0001) в задаче на вычитание (5c).

Скаты

Изображение №6

Все скаты преуспели в предварительном обучении в среднем в течение 21±5 сеансов, и им было разрешено участвовать в обучении сложению/вычитанию. Но лишь 3 особи после 68 ± 10 сеансов были отобраны для дальнейших опытов, так как именно они достигли желаемого уровня обучения. Примерный график продуктивности одного ската за все время эксперимента показан выше.

Во время тестов A, B и C индивидуальные выборы, объединенные в группу, показали, что скаты значительно чаще выбирали правильный стимул (+1/−1). В задаче на сложение в тесте А испытуемые были верны 58 из 60 раз (n = 3, p < 0.0001) и 54 из 60 раз (n = 3, p < 0.001) в задаче на вычитание (7а).


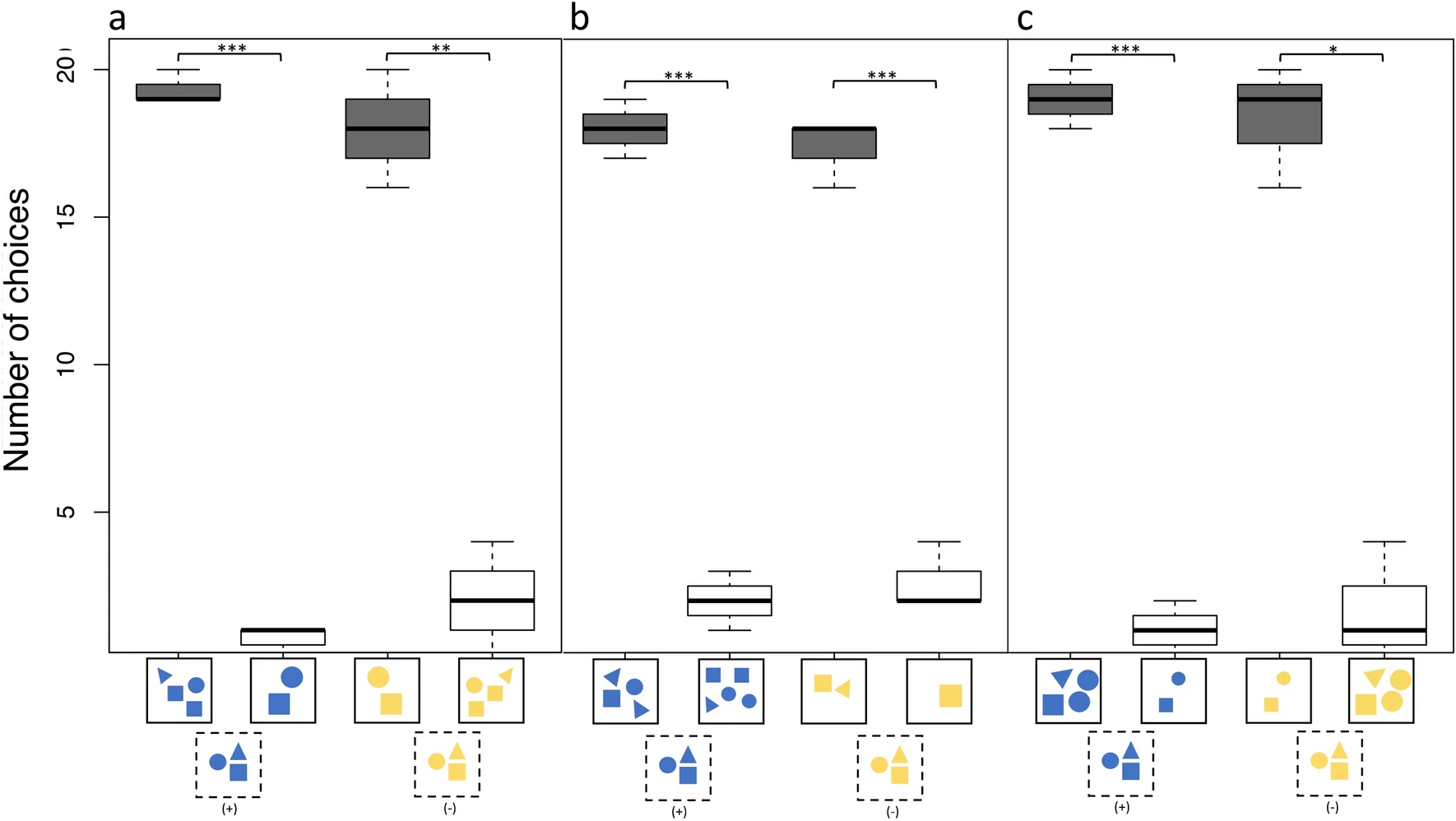
Изображение №7

В тесте B особи были верны 54 из 60 раз в задаче на сложение (n = 3, p < 0.0001) и 52 из 60 раз (n = 3, p < 0.0001) в задаче на вычитание (7b). Выборы в задаче на сложение в тесте С были правильными в 57 случаях из 60 (n = 3, p < 0.0001) и в 55 из 60 раз (n = 3, p < 0.01) в задаче на вычитание (7c).

Анализ результатов наблюдений

Цихлиды, как и скаты, успешно научились выполнять отсроченное задание на сопоставление с образцом в дополнение к выполнению простой арифметической задачи в зависимости от цвета первого предъявленного им тестового стимула. Тесты показали, что обучение не зависит от простого запоминания символов (тест А). Особи не просто научились выбирать наибольшее или наименьшее представленное число в зависимости от соответствующего цвета, вместо этого обучение было специфичным, т.е. наблюдалось прибавление или вычитание «единицы» (тест B).

В то время как групповые результаты были значительными для обоих видов во всех тестах, индивидуальные результаты все же различались. Как правило, оба вида выучили сложение легче, чем вычитание.

Цихлиды усвоили исходную задачу быстрее, чем скаты. Это может быть связано с более высокой экологической значимостью (цихлиды живут группами, а скаты — одиночки) или тем фактом, что цихлиды не были «чистыми» в начале экспериментов, поскольку ранее участвовали в других экспериментах на обучение. В результате задачу усвоили больше цихлид (80%), чем скатов (50%).

Любопытно то, что индивидуальные показатели скатов, как правило, превышали показатели цихлид, при этом большее число особей демонстрировало результаты значительно выше случайного во всех сценариях отдельных испытаний.

По мнению ученых, полученные результаты не являются чем-то удивительным, учитывая предыдущие когнитивные задачи, с которыми справлялись рыбы. Однако полученные результаты описывают новый уровень когнитивных способностей у этих существ. Задание с отложенным сопоставлением с образцом было сопряжено с арифметическим заданием, требующим как кратковременной памяти, числовых навыков, так и комбинированного использования обоих, в зависимости от задачи визуального распознавания (распознавания двух цветов).

В свете новых данных возникает новый вопрос — насколько большим должен быть мозг на самом деле для выполнения сложных когнитивных действий. Рыбы, у которых отсутствует неокортекс или столь же структурированный и во многих отношениях гомологичный птичий паллий, до сих пор обычно называют «примитивными» или «низшими» позвоночными. Получается, что неокортекс как таковой не нужен для выполнения сложных когнитивных навыков. Вместо этого несколько исследований показали, что различные паллиальные структуры участвуют в отдельных когнитивных действиях у рыб.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.

Эпилог

В рассмотренном нами сегодня труде ученые провели любопытные опыты, которые показали наличие у цихлид и скатов арифметических способностей. И те, и другие были успешны как в задачах на вычитание, так и на сложение.

Для существ, обладающих более развитым мозгом, подобные навыки не являются чем-то удивительным, но когда речь идет о рыбах, то их часто называют примитивными позвоночными, неспособными на такие когнитивные функции. Тем не менее результаты опытов доказывают обратное, из чего следует вывод, что неокортекс не так важен, как предполагалось ранее.

Авторы исследования также отмечают, что результаты их работы показывают еще один любопытный факт — человеку свойственно занижать интеллектуальные способности других видов. Особенно ярко это проявляется именно на примере существ, которые не являются нашими прямыми родственниками или же хотя бы млекопитающими.

В дальнейшем ученые намерены провести еще несколько экспериментов, дабы установить интеллектуальные способности и других существ, а также оценить предел этих способностей.

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?