Привет, Хаброжители! От создателя IBM Q. Квантовые вычисления заставляют нас изменить отношение к компьютерам. Кубиты способны решать задачи, которые еще совсем недавно казались неразрешимыми. Вы узнаете о принципиальных различиях между квантовыми и классическими вычислениями, вспомните матанализ, чтобы разобраться с такими понятиями, как суперпозиция, запутанность и интерференция, от алгоритмов и схем перейдете к физическим и техническим идеям, лежащим в основе создания железа для квантовых вычислений. Загляните в будущее и узнайте, как развитие технологий повлияет на нашу жизнь!

Прежде чем мы попробуем разобраться в том, как работают квантовые вычисления, придется обратиться к классике. И это нужно не только для сравнения. Я полагаю, что будущее — за гибридами классических и квантовых компьютеров.

Лучший способ усвоить что-то — начать с базовых принципов, а затем двигаться по восходящей. Это позволит вам самостоятельно рассуждать об осваиваемой теме, не полагаясь на механическое запоминание или ошибочные аналогии.

Симуляция

Можно ли симулировать квантовый компьютер на классическом компьютере? Если бы мы могли это сделать, то «квантовые вычисления» были бы всего лишь еще одним методом кодирования программного обеспечения на наших современных машинах.

В этом разделе мы поговорим о том, что вы должны учитывать, если захотите написать симулятор для манипулирования логическими кубитами.

Если у вас есть под рукой симулятор, например тот, который предоставляется квантово-вычислительной платформой Qiskit или онлайновой платформой IBM Q Experience, то вы можете использовать его для малых задач. Здесь мы в общих чертах рассмотрим вопрос о том, как можно было бы построить симулятор. Я предлагаю не законченный код на каком-либо конкретном языке программирования, а скорее список того, что нужно принять во внимание. Вы можете пропустить этот раздел, если такие задачи вас не интересуют.

Кубиты

Когда вы задумались о создании квантово-вычислительного симулятора, первое, что вам нужно решить, — это то, как вы представляете кубиты. С помощью того или иного варианта вы можете построить общую модель либо ее конкретизировать. Мы идем по пути общего случая. После того как вы закончите этот раздел, вы можете вернуться назад и подумать о том, как каждая из взаимосвязанных частей может быть оптимизирована вместе и по отдельности.

Мы хотим работать с более чем одним кубитом и поэтому не используем сферу Блоха. Состояние кубита хранится в двух комплексных числах, и вы можете хранить их в упорядоченном списке, массиве или похожей структуре. Если ваш язык или среда имеют математическо-векторный тип, то используйте его.

В то время как мы здесь, возможно, используем точное значение наподобие,

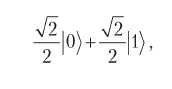
ваш язык или среда, вероятно, используют числа с плавающей запятой для вещественной и мнимой частей комплексного числа. Так что вышесказанное может равняться

0,7071067811865476 |0〉 + 0,7071067811865476 |1〉,

а сумма квадратов амплитуд вероятностей будет равна 1,0000000000000002. Вам необходимо отслеживать и, возможно, контролировать эту ошибку, если вы используете много кубитов или вентилей.

В случае очень малого симулятора вы должны рассмотреть возможность использования библиотеки символической математики, такой как SymPy [28]. Затраты времени и памяти могут оказаться слишком большими для вашего варианта использования. Кроме того, символические выражения могут быстро усложняться и запутываться, поэтому способность вашей системы упрощать эти выражения очень важна.

Если у вас есть n-битный квантовый регистр, то вам нужно представить вектор 2^n комплексных чисел. Если n = 10, то список из 1024 комплексных чисел использует 9024 байт. Для 20 кубитов это 8 697 464 байт, или приблизительно 8,3 Мбайт. Добавив всего лишь два кубита, вы получите 35 746 776, или 34 Мбайт.

Подумайте об этом: для одиночного состояния квантового регистра с 22 кубитами вам потребуется 34 Мбайт для его представления. Указанная величина становится экспоненциально больше и хуже, когда мы добавляем больше кубитов. Мы получаем более гигабайта в расчете на состояние при 27 кубитах. Растет не только объем памяти, но и время, необходимое для манипулирования всеми этими значениями. Ваш выбор алгоритмов на каждом уровне имеет решающее значение.

Дело обстоит еще хуже: размер матрицы для вентиля равен квадрату числа элементов в кете кубитного состояния.

Вы можете понизить эти цифры при помощи оптимизации, но экспоненциальный характер роста все равно вас догонит. Возможно, у вас получится сделать еще несколько кубитов, но симуляция в конечном итоге выдохнется.

Один из способов ее осуществить — использовать числа с плавающей запятой одинарной точности вместо двойной точности. Это ненадолго сэкономит память.

Мое предположение: общецелевая квантово-вычичлительная симуляция станет слишком большой и непрактичной по времени даже для суперкомпьютеров где-то на 40-м кубите. Если у вас очень специфическая задача, которую вы пытаетесь смоделировать, то вы можете упростить представляющие схему математические формулы. Точно так же, как выражение sin^2 (x) + cos^2 (x) сводится к гораздо более простой единице, математика для вашей схемы может стать меньше. И даже в этом случае, по моему мнению, вполне вероятно, что специализированная симуляция будет ограничена примерно 70–80 кубитами.

Симуляция хорошо подходит для экспериментов, обучения и отладки части квантовой схемы. Как только у нас появятся мощные и полезные настоящие квантовые компьютеры объемом более 50 кубитов или около того, потребность в симуляторах уменьшится — вероятно, вместе с их коммерческим рынком.

Рекомендуется использовать разреженное представление кубитов и кет-векторов. Действительно ли вам нужно 2^50 = 1 125 899 906 842 624 числа для представления состояния |0〉^⊗50? В конце концов, там есть только две части значимой информации, 0 и 50. Добавьте немного накладных расходов для представления разреженного кета, и вы сможете уместить все это в несколько байтов.

Вентили

Если кубиты — это векторы, то вентили — это матрицы. Наиболее прямолинейным способом реализации многопроводных схем является конструирование матрицы тензорного произведения для двух вентилей. Эти матрицы становятся довольно крупными: если у вас n кубитов, то ваши матрицы будут иметь размер 2^n × 2^n.

Для следующей подсхемы


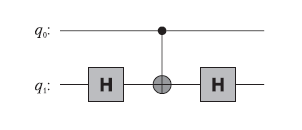
мы имеем произведение матриц, соответствующее ID ⊗ H,


как выполнить симуляцию измерения? Мы используем метод симулированной выборки с использованием случайных чисел из раздела 6.5.

Если существует один кет с ненулевой амплитудой, то эта амплитуда должна быть результатом измерения. Теперь предположим, что существуют две или более ненулевые амплитуды.

Вычислим вероятности, соответствующие каждому стандартному базисному кету. Если,


Еще раз напомню, что получение, например, E7 означает, что при измерении мы получаем результат |7〉.

Схемы

Для того чтобы симулировать схему, вам нужно каким-то образом ее представить. Подумайте о проводной модели, а затем о горизонтальных шагах слева направо, где вы размещаете и выполняете вентили.

Многокубитные вентили охватывают провода, поэтому вам нужно указать проводные входы и выходы. В процессе вам нужно выполнить проверку ошибок, чтобы убедиться, что два вентиля на одном шаге не задействовали одинаковые входные и выходные провода.

Я рекомендую вам начать с API, интерфейса прикладного программирования для набора подпрограмм, которые находятся поверх вашего внутреннего представления схем. Если вы начнете с разработки нового языка для написания схем, то, скорее всего, потратите больше ранних циклов кодирования на сам этот язык, чем на симулятор.

Кодирование симулятора

Если вы решите закодировать квантовый симулятор, то вот несколько советов.

— Не утруждайте себя, за исключением тех случаев, когда вы хотите сделать симулятор в качестве образовательного проекта или же когда у вас есть блестящая новая идея. Существует множество симуляторов, многие из которых с открытым исходным кодом, например в Qiskit.

— Не начинайте с оптимизации схем. Будет достаточно сложно отладить код, который должен выполнять последовательность операций, которую вы хотите.

— Когда вы все-таки начнете оптимизацию, в первую очередь обратите внимание на простые действия, такие как устранение расположенных подряд вентилей, которые ничего не делают. Три примера тому: H H, X X и Z Z.

— Не ищите тензорное произведение матриц до тех пор, пока у вас не будет проводной операции наподобие CNOT.

— Постройте эффективные подпрограммы, которые симулируют стандартные вентильные комбинации. Например, не стройте CNOT из вентиля Тоффоли, но обеспечьте наличие вентиля Тоффоли в своей коллекции.

— Углубитесь в то, как квантовые вентили конструируются из более примитивных вентилей. Например, освойте вентиль Клиффорда и разберитесь в том, как его симулировать. Обратите внимание, что это потребует более глубоких познаний в области квантовых вычислений и компьютерных наук [4], [5].

Дополнительные сведения
Еще раз хочу подчеркнуть свою мысль о том, что совсем не обязательно кодировать свой собственный симулятор: вбив в поисковой строке в интернете «список квантовых симуляторов» (или list of quantum simulators), вы увидите десятки симуляторов на многочисленных языках программирования, многие из которых будут с открытым исходным кодом.

Кот

А теперь поговорим о знаменитой дискуссии, которая развернулась в 1930-х годах. Мы воспользуемся ею как примером симулирования квантовой физики с помощью квантовых вычислений.

В 1935 году физик Эрвин Шрёдингер предложил мысленный эксперимент, который дал импульс к развитию глубокой научной и философской мысли почти на столетие, а также породил множество дурацких шуток. Мысленные эксперименты широко распространены среди математиков и физиков.

Основная предпосылка мысленного эксперимента заключается в том, что идея — это не то, что вы действительно собираетесь сделать, а то, что вы хотите продумать, чтобы понять последствия и сделать выводы.

Данный эксперимент был попыткой показать, как копенгагенская интерпретация, выдвинутая Нильсом Бором и Вернером Гейзенбергом в конце 1920-х годов, может привести к нелепому выводу для больших объектов. И в то же время это одно из популярных толкований того, как и почему работает квантовая механика, хотя есть и другие.

Вопрос 11.9.1

Какое отношение Копенгаген имеет к квантовой механике?

Настройка

В большой стальной ящик, в котором предостаточно воздуха, чтобы кот мог дышать в течение нескольких часов, мы помещаем небольшое количество радиоактивного материала, который имеет 0,5 вероятности распада одного атома и испускает одну частицу в час.

Мы также помещаем туда счетчик Гейгера, который способен обнаружить это единственное излучение, плюс подключенный молоток, который может разбить закрытый флакон с цианистым ядом. Если счетчик Гейгера что-нибудь обнаружит, то молоток качнется и цианид будет выброшен в воздух.

Теперь мы помещаем очаровательного, но озадаченного кота в ящик и запечатываем крышку.
Не стесняйтесь заменить кота чем-то другим, что не выживет в присутствии цианида.

Ожидание

Пока время идет свои чередом, мы задаемся вопросом о состоянии кота. Все ли у него хорошо, или он уже отошел в мир иной? Распался ли атом и привело ли это в действие молоток?

Мы не узнаем, пока не посмотрим. Насколько нам известно, кот находится в суперпозиции мертвого и живого. Открыв крышку и пронаблюдав за тем, что происходит в ящике, мы заставляем суперпозицию коллапсировать в |мертвый〉 = |0〉 либо |живой〉 = |1〉. Это соответствует копенгагенской интерпретации.

В многомировой интерпретации, когда появилась возможность выбора, были созданы две реальности. В одном мире кот мертв, в другом — нет.

Теперь выразим эту ситуацию на языке квантовой схемы.

Схема

Рассмотрим вот эту простую схему с двумя вентилями CNOT:

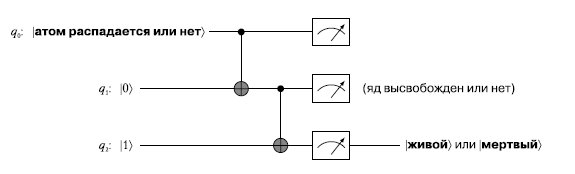
Для q0 входное состояние |0〉 означает, что в момент выполнения схемы ни один атом не распадается, а |1〉 — что испускается частица.

q1 устанавливается в начальное состояние |0〉, но инвертируется в |1〉, если атом распадается. Это приводит к тому, что молоток разбивает флакон, и цианид попадает в воздух.

Для q2 кот начинает в состоянии |живой〉 = |1〉. Конечное состояние кота может переключиться в |мертвый〉 = |0〉, только если высвобождается яд.

Вопрос 11.9.2

Поэкспериментируйте с состояниями Белла, чтобы ввести запутанность. Узнали ли вы что-нибудь новое о компонентах этого эксперимента?

Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.

Для Хаброжителей скидка 30% по купону — Сатор