Зачем нужен этот пост?

Задумка данного поста заключается в том, чтобы коротко и ясно объяснить как работают на графах данные алгоритмы. То есть целью поста в первую очередь является понимание, а не детали реализации в коде.

Зачем нужны данные алгоритмы?

Обход в ширину и обход в глубину - два алгоритма, являющиеся основой для большинства сложных алгоритмов, имеющих реальное применение в жизни. Не задумываясь, мы сталкиваемся с графами постоянно. Как самый банальный пример - навигатор. Построение маршрута - уже задача, в которой используются данные алгоритмы.

Обход в глубину (Depth-First Search, DFS)

Один из основных методов обхода графа, часто используемый для проверки связности графа, поиска цикла и компонент сильной связности и для топологической сортировки. Отбросим все эти сложные слова до поры до времени, а пока посмотрим, что же делает DFS и как он это делает. Будем рассматривать реализацию на списке смежности как самую легкую для понимания. Вкратце напомню, что список смежности - это один из способов представления графа, который выглядит примерно так:

Для каждой вершины (первый столбик) мы составляем список смежных ей вершин, то есть список вершин с которыми у данной есть общие ребра(ребро инцидентное данным вершинам).

Теперь собственно к самому алгоритму, принцип его работы совпадает с его названием, данный алгоритм идет "внутрь" графа, до того момента как ему становится некуда идти, затем возвращается в предыдущую вершину и снова идет от нее до тех пор, пока есть куда идти. И так далее. Для понимания данного алгоритма нам потребуются 3 цвета, один будет обозначать, что вершину мы еще не посетили, второй что посетили и ушли, а третий, что посетили и не смогли идти дальше и начинаем возвращаться обратно.

Стартуем из любой вершины, например, из первой. Идем по списку смежности. Из 1 вершины попадаем во вторую, переходим в ее список смежности, не забываем красить 1 вершину в серый, так как мы ее посетили и ушли дальше. Из второй вершины идем в любую из списка смежности второй вершины, например в 3. Красим 2 в серый и идем в список смежности 3-й вершины. А в нем ничего нет. В таком случае мы понимаем, что дальше нам идти не куда, пора возвращаться.

Красим 3 в черный так как нам идти некуда(нет белых вершин, в которые мы могли бы пойти из 3). Возвращаемся в 2 и в ее список смежности, видим что там еще есть вершина 4, выдвигаемся туда, оттуда можно пойти только в 1, но она уже серая, то есть мы там уже были. Алгоритм начнет рекурсивно откатываться назад перекрашивая все вершины в черный, думаю принцип уже понятен.

Псевдокод

Что здесь происходит? Все то, что мы уже видели, только в коде. G.Adj - список смежности данного графа. Для каждой вершины если она еще не посещена - красим ее в серый, то есть в true ее поле visited, таким образом пройдемся по всем вершинам. Зачем мы в init() вызываем dfs для каждой вершины? Мы можем не угадать с первой вершиной, как например в графе сверху, если бы мы начали с вершины 3, дфс бы закончился сразу, так как из нее нет исходящих дуг.

Обход в ширину (breadth-first search, BFS)

Систематически обходит все вершины графа. В чем его отличие от обхода в глубину? Обход в глубину "перепрыгивает" между строками списка смежности по 1 вершине за раз, а обход в ширину сразу по всем возможным, посмотрим как он работает на примере:

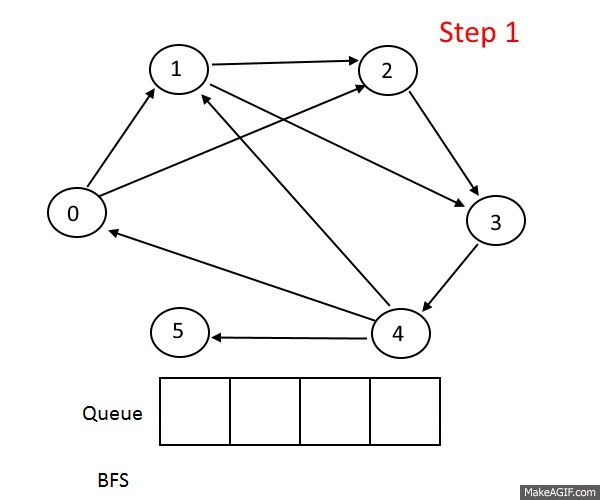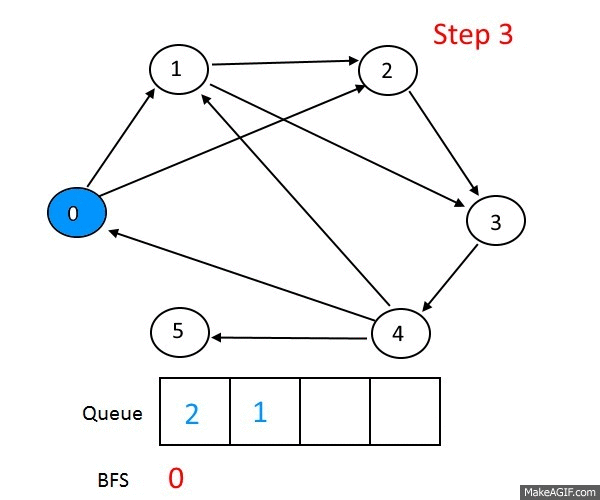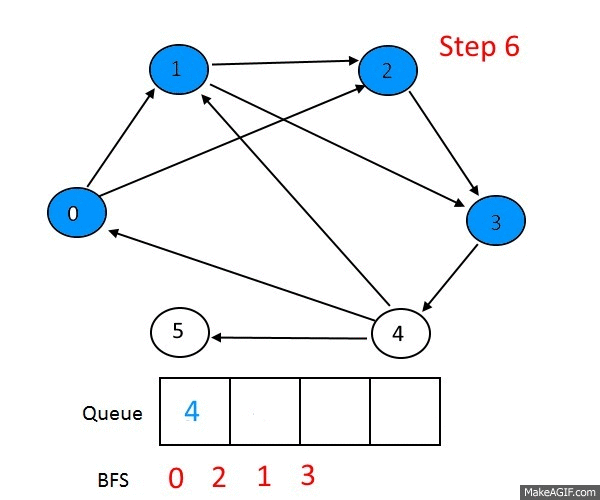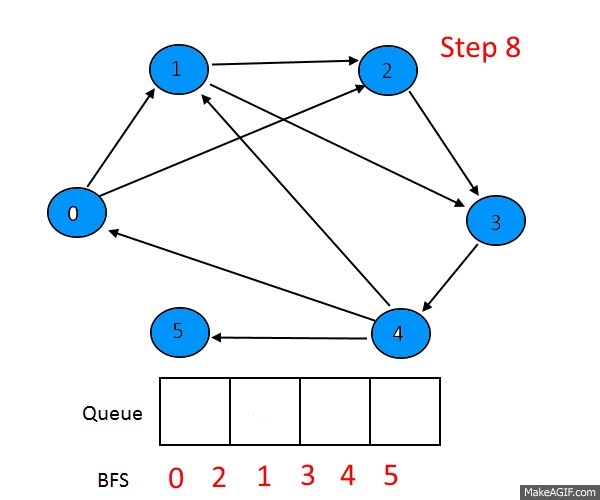
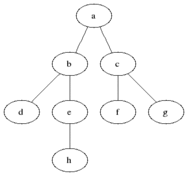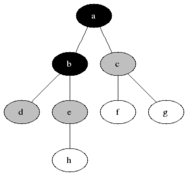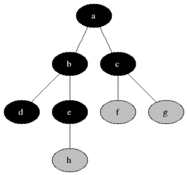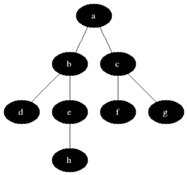
Сначала мы проходимся по всем вершинам смежным со стартовой, потом по всем, смежным со смежными стартовой и так далее. Вот еще один пример, который как мне кажется более наглядно показывает различие обходов в глубину и ширину: в 1-м граф как бы обходится равномерно.

Псевдокод с краткими пояснениями:

Заключение

Два этих алгоритма очень важны для понимания. Искренне надеюсь, что данный пост дал читателю хотя бы примерное представление о том, как работают обходы в глубину и ширину, так как полное понимание вы получите только после применения этих алгоритмов на практике.