Мы меняем
std::sort в библиотеке libcxx проекта LLVM. В этой статье мы подробно расскажем о том, как мы пришли к этому решению и какими будут возможные последствия, о багах, с которыми вы можете столкнуться в примерах из open source. Мы покажем несколько бенчмарков, объясним, почему вообще это сделали и чего это нам стоило, на примерах закона Хайрама и обучения с подкреплением. Все изменения выложены в open source, поэтому я свободно могу о них рассказывать.Эта статья разделена на три части. Первая — это подробная история недавнего прошлого сортировки в стандартных библиотеках C++. Вторая расскажет об усилиях, необходимых для перехода от одного алгоритма сортировки к другому с различными багами. В третьей мы объясним выбранную нами реализацию и все внесённые нами оптимизации.
Глава 1. История
Алгоритмы сортировки активно исследовались ещё с самого зарождения computer science1. В частности, люди пытались оптимизировать среднее количество сравнений в наихудшем случае и в определённых случаях, например, при частично отсортированных данных. Существует даже алгоритм сортировки, основанный на машинном обучении2 — он пытается прогнозировать позицию, где должны находиться элементы, и его бенчмарки весьма впечатляют! Очевидно одно — алгоритмы сортировки эволюционируют даже сейчас, улучшая постоянные коэффициенты и снижая количество сравнений.
Во всех языках программирования есть вызовы сортировки, и выбор используемого алгоритма зависит от библиотеки. О различиях в языках мы поговорим позже. Споры о том, какая сортировка лучше, не прекращаются на Hackernews3, в статьях4 и репозиториях5.
Дональд Кнут сказал:
Было бы здорово, если бы только один-два способа сортировки доминировали над остальными, вне зависимости от сферы применения и используемого компьютера. Однако, на самом деле каждый способ имеет собственные любопытные достоинства. […] Поэтому мы должны помнить практически все алгоритмы, потому что в некоторых случаях они оказываются наилучшими. — Дональд Кнут, «Искусство программирования», том 3
История C++
std::sort появилась в C++ с момента изобретения Александром Степановым9 так называемой «STL», а в стандарте C++ того времени была интересная инновация под названием «сложность». В то время сложность была установлена на At the time the complexity равной Как была реализована первая std::sort?
В ней использовался простой quicksort с медианой 3 (медиана от (первого, среднего, последнего) элементов). Если рекурсия затрагивает менее 16 элементов, она прекращается и в конце использует сортировку вставками, поскольку считается, что она быстрее для небольших массивов.
Вы видите последний этап, на котором она пытается «сгладить» неточные блоки размера 16.
Небольшая проблема quicksort
Да, действительно правда, что quicksort в среднем имеет сложность

Это даёт нам возможность самомодифицирования массива, или, иными словами, принятия решений в процессе вызова функции comp и внедряет наихудшую временную сложность для любых данных. Ниже мы объясним данный код:
int quadratic(int size) {
int num_solid = 0;
// gas означает "бесконечность"
int gas = size + 1;
int comparison_count = 0;
std::vector<int> indices(size);
std::vector<int> values(size);
// индексы - это 0, 1, …, size
// все значения бесконечны
for (int i = 0; i < size; ++i) {
indices[i] = i;
values[i] = gas;
}
// Принудительно обеспечиваем равномерное распределение входящих данных!
std::random_device rd;
std::mt19937 g(rd());
std::shuffle(indices.begin(), indices.end(), g);
sort(indices.begin(), indices.end(), [&](int x, int y) {
comparison_count += 1;
// Если оба бесконечны, задать левое.
// В противном случае gas всегда больше
if (values[x] == gas && values[y] == gas) {
values[x] = num_solid++;
return true;
} else if (values[x] == gas) {
return false;
} else if (values[y] == gas) {
return true;
} else {
return values[x] < values[y];
}
});
return comparison_count;
}Если мы рассмотрим любой алгоритм быстрой сортировки со следующей семантикой:
- Находим некий опорный
среди
(константа).
- Разделяем по опорному элементу, выполняем рекурсию с обоих сторон.
то значение «gas» обозначает неизвестное, бесконечность; значение левого элемента присваивается только при сравнении двух неизвестных элементов, и если один из элементов gas, то он всегда больше.
На первом шаге выберем какой-то опорный элемент из не более чем
На шаге
Если мы запустим этот код с оригинальной STL10, то точно получим квадратичное количество сравнений.
int main(int argc, char** argv) {
std::cout << "N: comparisons\n";
for (int i = 100; i <= 6400; i *= 2) {
std::cout << i << ": " << quadratic(i) << "\n";
}
return 0;
}
/*
N: сравнения
100: 2773
200: 10623
400: 41323
800: 162723
1600: 645523
3200: 2571123
6400: 10262323
*/Какую бы рандомизацию мы не вносили, даже quicksort-реализация
std::sort в среднем квадратична (с учётом произвольного компаратора) и реализация, строго говоря, не будет соответствовать требованиям.Показанный выше пример не пытается ничего доказать и является довольно искусственным, хоть и существуют некоторые проблемы с формулировками в стандарте относительно «среднего» случая.
Отход от квадратичного поведения
Тестирование наихудшего случая Quicksort впервые было проведено Дугласом Макилроем11 в 1998 году, оно называлось “Antiquicksort”. В конечном итоге оно повлияло на то, чтобы перейти к сложности
std::sort Однако на этом история не закончилась.
Соответствуют ли требованиям современные стандартные библиотеки C++?
В стандарте C++ есть не так много мест с формулировкой «в среднем». Ещё одним примером этого является вызов
std::nth_element.Что такое std::nth_element?
Вы можете догадаться, что функция находит
n-ный элемент в интервале. Если конкретнее, то std::nth_element(first, nth, last, comp) — это алгоритм частичной сортировки, изменяющий порядок элементов в интервале следующим образом:- Элемент, на который указывает
nth, меняется на тот элемент, который находится в этой позиции, если[first, last)отсортированы. - Все элементы до этого нового элемента
nthменьше или равны элементам после нового элементаnth.
Вы видите, что в сложности по-прежнему указывается «в среднем».

Это решение используется из-за применяемого алгоритма 12. Однако этот алгоритм восприимчив к одинаковым трюкам в реализациях и GNU, и LLVM.

В версии LLVM/clang он очевидно деградирует до квадратичного поведения, в версии GNU
Однако для нахождения элемента
nth существует не так много линейных алгоритмов наихудшего случая, один из них — это алгоритм median of medians16, имеющий очень плохую константу. Нам потребовалось около двадцати лет, чтобы найти что-нибудь действительно подходящее, и это удалось Андрею Александреску14. В моём посте об алгоритмах выбора эта тема изложена достаточно подробно (и есть реализация, созданная самим Андреем!). Мы выявили большое ускорение на реальных данных для реальных SQL-запросов типа SELECT * from table ORDER BY x LIMIT N.Miniselect: Practical and Generic Selection Algorithms
Что случилось с std::sort?
В ней начали использовать интроспективную сортировку, или introsort, поверх слишком многих уровней quicksort, если конкретнее, то
Вот наихудший случай сортировки introsort для реализации GNU:
История LLVM
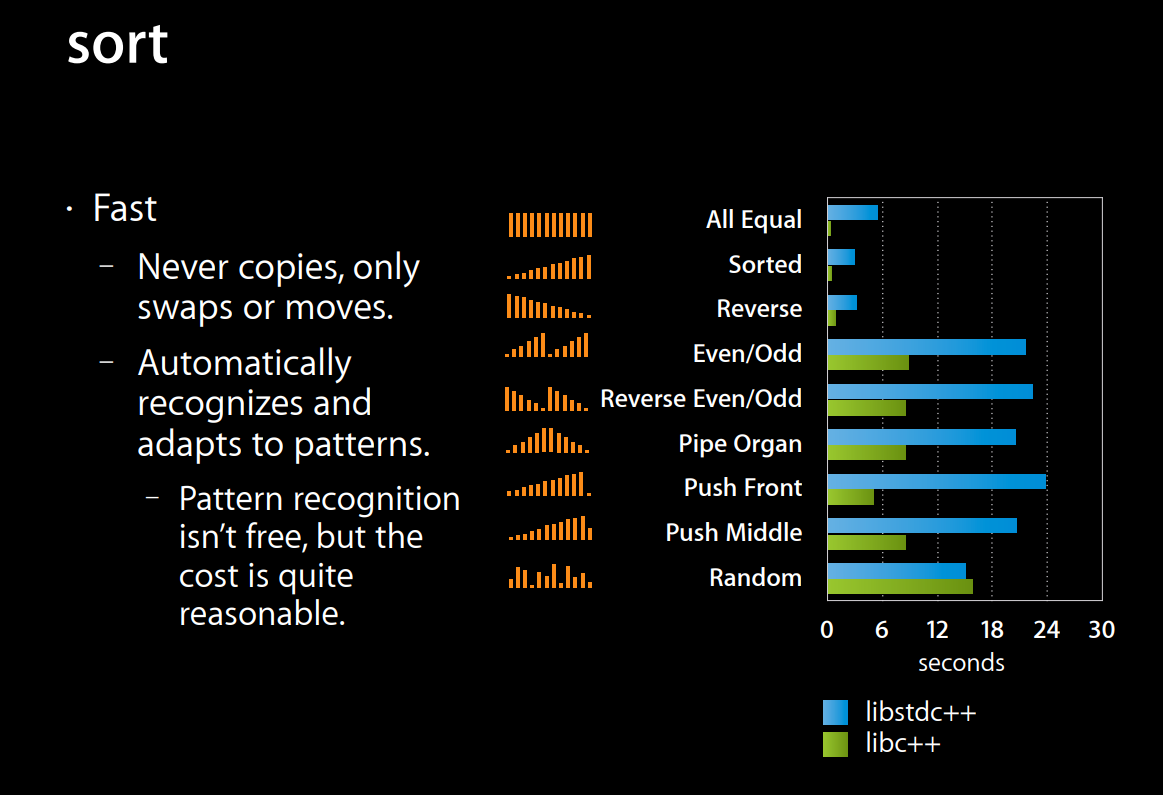
Когда LLVM попытался собрать версию STL для C++0x, Ховард Хиннант создал презентацию6 о том, как проходит реализация. В то время мы нашли очень интересные бенчмарки и всё больше бенчмарков сортировок на разных паттернах данных.

Слайд Ховарда Хиннанта о сортировке, 2010 год
Это заставило нас задуматься о том, что делает сортировку успешной и эффективной. Очевидно, что не все данные случайны и в продакшене возникают некоторые паттерны, насколько важно их балансировать и распознавать?
Например, даже в Google, поскольку мы используем много protobuf, встречаются частые вызовы
std::sort, исходящие от библиотеки7, сортирующей все метки представленных в сообщении полей:struct FieldNumberSorter {
bool operator()(const FieldDescriptor* left,
const FieldDescriptor* right) const {
// Сортируем по порядку меток.
return left->number() < right->number();
}
};
void Reflection::ListFieldsMayFailOnStripped(
const Message& message, bool should_fail,
std::vector<const FieldDescriptor*>* output) const {
// Обходим все поля по порядку их объявления.
for (int i = 0; i <= last_non_weak_field_index; i++) {
const FieldDescriptor* field = descriptor_->field(i);
if (FieldSize(message, field) > 0) {
output->push_back(field);
}
}
// Сортируем по их номеру метки
std::sort(output->begin(), output->end(), FieldNumberSorter());
}message GoogleMessage2 {
// тип имя метка
// vvvvvv vvvvvv vvv
optional string field1 = 1;
optional int64 field3 = 3;
optional int64 field4 = 4;
optional int64 field30 = 30;
optional bool field75 = 75 [default = false];
// Немного не по порядку, 1, 3, 4, 30, 75, 6, 2
optional string field6 = 6;
optional bytes field2 = 2;
// …
}Это первое важное наблюдение: нам нужно распознавать «почти отсортированные» паттерны, когда они встречаются. Очевидными случаями являются возрастание/убывание, небольшие примеси их, а также множественные последовательные серии увеличивающихся или уменьшающихся значений. TL;DR; нам не удалось достичь в этом особо хороших результатов, однако большинство современных алгоритмов может распознавать самые очевидные случаи.
Теория: presortedness
Показатель Presortedness впервые был формально описан в 8:

Условие 1 — это нормализатор, условие 2 указывает, что нас должны интересовать только сравнения, а не элементы, условие 3 показывает, что если мы можем отсортировать надпоследовательность, то мы сможем и отсортировать подпоследвательность за меньшее количество сравнений, условие 4 — верхний предел для сортируемых частей: вы должны иметь возможность отсортировать
Существует множество оценок presortedness, например
- m01: 1 — если не отсортировано, 0 — если отсортировано. Довольно глупая оценка.
- Block: количество элементов в последовательности, за которыми не следует тот же элемент в отсортированной последовательности.
- Mono: минимальное количество элементов, которое нужно удалить из X, чтобы получить отсортированную подпоследовательность, что соответствует |X| минус размер наибольшей неуменьшающейся подпоследовательности X.
- Dis: максимальное расстояние, определяемое инверсией.
- Runs: количество неуменьшающихся изменений в X минус один.
- И т. д.
Некоторые оценки presortedness лучше других, то есть если существует алгоритм, оптимальный для определённой оценки (под оптимальностью понимается, что количество сравнений

NeatSort — A practical adaptive algorithm
К сожалению, среди всех приведённых выше оценок только Mono, Dis и Runs выполянются за линейное временя (другие за
Что ж, наверно, вам надоела теория и вы готовы к чему-то более практичному.
Продолжение истории LLVM
Так как библиотека LLVM libcxx была разработана до C++11, первая версия тоже основывалась на quicksort. В чём заключалось отличие от сортировки GNU?
Реализация libcxx обрабатывала несколько конкретных случаев особым образом. Коллекции длиной 5 или меньше сортировались при помощи специальных самописных сортировок на основе сравнений.
sort4.cpp:template <class _Compare, class _ForwardIterator>
unsigned __sort4(_ForwardIterator __x1, _ForwardIterator __x2, _ForwardIterator __x3, _ForwardIterator __x4,
_Compare __c) {
unsigned __r = _VSTD::__sort3<_Compare>(__x1, __x2, __x3, __c);
if (__c(*__x4, *__x3)) {
swap(*__x3, *__x4);
++__r;
if (__c(*__x3, *__x2)) {
swap(*__x2, *__x3);
++__r;
if (__c(*__x2, *__x1)) {
swap(*__x1, *__x2);
++__r;
}
}
}
return __r;
}sort5.cpp:template <class _Compare, class _ForwardIterator>
unsigned __sort5(_ForwardIterator __x1, _ForwardIterator __x2, _ForwardIterator __x3,
_ForwardIterator __x4, _ForwardIterator __x5, _Compare __c) {
unsigned __r = _VSTD::__sort4<_Compare>(__x1, __x2, __x3, __x4, __c);
if (__c(*__x5, *__x4)) {
swap(*__x4, *__x5);
++__r;
if (__c(*__x4, *__x3)) {
swap(*__x3, *__x4);
++__r;
if (__c(*__x3, *__x2)) {
swap(*__x2, *__x3);
++__r;
if (__c(*__x2, *__x1)) {
swap(*__x1, *__x2);
++__r;
}
}
}
}
return __r;
}При некоторых типах данных коллекции длиной до 30 сортировались вставками. Тривиальные типы достаточно легко менять местами и ассемблерный код для них вполне подходит.
Есть специальный случай обработки коллекций, большинство элементов которых равно, и для коллекций, которые почти отсортированы. Алгоритм пытается использовать сортировку вставками до предела в 8 перестановок: если во время внешнего цикла мы встречаем больше 8 парных элементов, где
const unsigned __limit = 8;
unsigned __count = 0;
for (_RandomAccessIterator __i = __j + difference_type(1); __i != __last; ++__i) {
if (__comp(*__i, *__j)) {
value_type __t(_VSTD::move(*__i));
_RandomAccessIterator __k = __j;
__j = __i;
do {
*__j = _VSTD::move(*__k);
__j = __k;
} while (__j != __first && __comp(__t, *–__k));
*__j = _VSTD::move(__t);
if (++__count == __limit)
return ++__i == __last;
}
__j = __i;
}Сортировка libcxx LLVM при случайных данных
Однако, если посмотреть на входящие данные с возрастанием, то мы видим, что libstdcxx выполняет множество необязательной работы по сравнению с сортировкой libcxx, что на практике важно. Во-первых, она выполняется в 4,5 раза быстрее!
libcxx для возрастающих данных
libstdcxx для возрастающих данных
Последнее отличие заключается в том, что медиана, равная 5, выбирается, когда количество элементов в quicksort partition больше 1000. Больше никаких отличий; для меня самое большое влияние этой сортировки заключается в том, что она пытается распознавать стандартные паттерны, что затратно, но во многих реальных ситуациях даёт множество преимуществ.
Когда мы в Google сменили libstdcxx на libcxx, то заметили существенные улучшения (на десятки процентов) во времени, потраченном на
std::sort. С тех пор алгоритм не менялся, но данные, которые он обрабатывал, увеличивались.Проблема квадратичности
Так как libcxx LLVM разрабатывалась для C++03, первая реализация была нацелена на средний случай, о котором мы говорили выше. К этой проблеме обращались несколько раз, в 2014, 2017 и 2018 годах17, 18.
В конечном итоге мне удалось реализовать такое же улучшение, которое в библиотеке GNU добавили с помощью introsort. Мы добавили в алгоритм дополнительный параметр, определяющий максимальную глубину рекурсии, на которую может уйти алгоритм, после которой оставшаяся последовательность пути сортируется при помощи heapsort. Количество допустимых разделений задаётся равным
void
__introsort(_RandomAccessIterator __first, _RandomAccessIterator __last,
difference_type __depth) {
// …
while (true) {
if (__depth == 0) {
// Откат к heapsort, как предложено в Introsort.
_VSTD::__partial_sort<_Compare>(__first, __last, __last);
return;
}
–__depth;
// …
}
template <typename _Number>
inline _Number __log2i(_Number __n) {
_Number __log2 = 0;
while (__n > 1) {
__log2++;
__n >>= 1;
}
return __log2;
}
void __sort(_RandomAccessIterator __first, _RandomAccessIterator __last) {
difference_type __depth_limit = 2 * __log2i(__last – __first);
_VSTD::__introsort(__first, __last, __depth_limit);
}Сколько случаев из реального мира попало в heapsort?
Также нам было интересно, какая часть производительности ушла на глубокие уровни quicksort, и мы убедились, что один из нескольких тысяч всех вызовов
std::sort откатывается к heapsort.Это было довольно необычное открытие. Оно не показало никаких статистически значимых улучшений, т. е. не было найдено никаких очевидных или существенных квадратических улучшений. На самом деле Quicksort вполне хорошо работает с реальными данными, однако этот алгоритм может подвергаться эксплойтам.
Глава 2. Заменить сортировку легко, не правда ли?
Поначалу кажется, что легко просто поменять реализацию и выиграть в ресурсах: сортировка имеет порядок и, например, если вы сортируете integer, то API не волнует ваша реализация; ему достаточно, чтобы интервал был упорядочен правильно.
Однако C++ API может получать функции сравнения, которые для простоты могут быть лямбда-функциями. Мы называем их «компараторами». Они могут различными способами нарушать наши допущения о детерминированности сортировки. Иногда я называю эту проблему «ничья может решаться по-разному».
std::vector<std::pair<int, int>> first_elements_equal{{1, 1}, {1, 2}};
std::sort(first_elements_equal.begin(),
first_elements_equal.end(),
[](const auto& lhs, const auto& rhs) {
// Сравнение только с частью отсортированных данных.
return lhs.first < rhs.first;
});
// Сериализируем или делаем допущения обо всех данных.
// Ошибка, может быть или 1, или 2.
assert(first_elements_equal[0].second == 1);В более серьёзных примерах могут использоваться SQL-запросы такого типа:
| id_1 | id_2 |
| 0 | 3 |
| 0 | 3 |
| 0 | 2 |
| 0 | 2 |
| 0 | 3 |
| 1 | 1 |
| 1 | 3 |
create table example (id_1 integer, id_2 integer);
— Insert lots of equal id_1
insert into example (id_1, id_2) values (1, 1);
insert into example (id_1, id_2) values (0, 3);
insert into example (id_1, id_2) values (0, 2);
insert into example (id_1, id_2) values (0, 3);
insert into example (id_1, id_2) values (0, 2);
insert into example (id_1, id_2) values (0, 3);
insert into example (id_1, id_2) values (1, 3);
— Order only by the first element, second
— is undefined for equal first elements.
select * from example order by id_1;| id_1 | id_2 |
| 0 | 3 |
| 0 | 2 |
| 0 | 3 |
| 0 | 2 |
| 0 | 3 |
| 1 | 1 |
| 1 | 3 |
Результат MySQL
И мы знаем, что пользователию любят писать золотые тесты для подобных запросов. Однако несмотря на то, что никто не гарантирует порядок равных элементов, пользователи зависят от такого поведения, поскольку он может быть закопан в коде, о котором они никогда не слышали. Это классический пример закона Хайрама.
При достаточном количестве пользователей API, не важно, что вы обещаете в контракте: все наблюдаемые поведения вашей системы будут зависеть от кого-то. — Хайрам Райт
Если различия слишком велики, золотые тесты могут сбивать с толку: мы что-то ломаем или тест слишком хрупкий, чтобы показывать что-то полезное? Золотые тесты непохожи на типичные юнит-тесты, поскольку они не принуждают ни к какому поведению. Они просто дают нам знать, что результат работы сервиса изменился. Нет никакого контракта о значении этих изменений; пользователь сам должен решать, что он хочет делать с этой информацией.
Когда мы попытались найти все такие случаи, то поняли, что из-за этого миграцию почти невозможно автоматизировать — откуда мы знаем, что именно эти изменения нужны нашим пользователям? В конечном итоге мы получили довольно суровый урок о том, что даже незначительные изменения в способе использования примитивов приводят к проблемам с золотыми тестами. Лучше использовать вместо золотых тестов юнит-тесты или уделять больше внимания детерминированности написанного кода.
Как найти все зависимости равных элементов?
Поскольку равные элементы в основном неразличимы при функциях сравнения (мы нашли только горстку примеров компараторов, вносящих изменения в массив в процессе), достаточно рандомизировать интервал перед самим вызовом
std::sort. Вы можете самостоятельно вычислить вероятности и доказать, что этого достаточно.Мы решили реализовать такую функциональность в LLVM в режиме отладки20 для вызовов
std::sort, std::nth_element, std::partial_sort.// _LIBCPP_DEBUG_RANDOMIZE_RANGE - это std::shuffle
template <class _RandomAccessIterator, class _Compare>
void sort(_RandomAccessIterator __first, _RandomAccessIterator __last,
_Compare __comp) {
// Рандомизируем интервал.
_LIBCPP_DEBUG_RANDOMIZE_RANGE(__first, __last);
typedef typename __comp_ref_type<_Compare>::type _Comp_ref;
// Вызываем внутреннюю сортировку.
_VSTD::__sort<_Comp_ref>(_VSTD::__unwrap_iter(__first),
_VSTD::__unwrap_iter(__last), _Comp_ref(__comp));
}
template <class _RandomAccessIterator, class _Compare>
void nth_element(_RandomAccessIterator __first, _RandomAccessIterator __nth,
_RandomAccessIterator __last, _Compare __comp) {
// Рандомизируем интервал.
_LIBCPP_DEBUG_RANDOMIZE_RANGE(__first, __last);
typedef typename __comp_ref_type<_Compare>::type _Comp_ref;
// Вызываем внутреннюю nth_element.
_VSTD::__nth_element<_Comp_ref>(__first, __nth, __last, __comp);
// Обе части разделения не имеют требований к упорядочиванию.
_LIBCPP_DEBUG_RANDOMIZE_RANGE(__first, __nth);
if (__nth != __last) {
_LIBCPP_DEBUG_RANDOMIZE_RANGE(++__nth, __last);
}
}
template <class _RandomAccessIterator, class _Compare>
void partial_sort(_RandomAccessIterator __first, _RandomAccessIterator __middle,
_RandomAccessIterator __last, _Compare __comp) {
// Рандомизируем интервал.
_LIBCPP_DEBUG_RANDOMIZE_RANGE(__first, __last);
typedef typename __comp_ref_type<_Compare>::type _Comp_ref;
_VSTD::__partial_sort<_Comp_ref>(__first, __middle, __last, __comp);
// Замыкающая часть не имеет требований к упорядочиванию.
_LIBCPP_DEBUG_RANDOMIZE_RANGE(__middle, __last);
}Техники получения порождающих значений
Для использовали для получения порождающих значений генератора случайных чисел технику
ASLR (address space layout randomization)21, при которой статические переменные будут находиться по случайным адресам при запуске программы и мы можем использовать его в качестве seed. Это обеспечивает ту же гарантию стабильности при прогоне программы, но не при разных прогонах, например тесты могут оказаться слоистыми и может показаться, что они сломались. Для платформ, не поддерживающих ASLR, seed при сборке делается фиксированным. Использование других техник от заголовка <random> было невозможным, поскольку заголовок <algorithm> рекурсивно зависел от <random> и в такой низкоуровневой библиотеке мы реализовали очень простой линейный генератор.static uint_fast64_t __seed() {
// адрес статической переменной может быть рандомизирован, если сборка выполняется с ASLR.
static char __x;
return reinterpret_cast<uintptr_t>(&__x);
}Такая рандомизация была включена в режиме отладочной сборки, поскольку во всех случаях при перетасовке элементов снижение производительности может быть существенным.
Опасность partial и nth
Кроме того, если приглядеться к показанным выше изменениям в рандомизации, то можете заметить разницу между
std::nth_element и std::partial_sort. Она может запутать.std::partial_sort и std::nth_element имеют различие в значении их параметров, в котором легко запутаться. Обе получают 3 итератора:-
begin— начало интервала -
nthormiddle— значение (и имя) этого параметра различается в этих функциях -
end— конец интервала
В функции
std::partial_sort средний параметр называется middle, он указывает прямо на место после части интервала, которая должна быть отсортирована. Это значит, что мы не знаем, на какой элемент будет указывать middle – мы только знаем, что это будет один из элементов, которые не нужно сортировать.В функции
std::nth_element этот средний параметр называется nth. Он указывает на единственный элемент, который будет отсортирован. Для всех элементов в [begin, nth) мы знаем лишь то, что они будут меньше или равны *nth, но не знаем, в каком порядке они будут находиться.Это значит, что если мы хотим найти 10-й по меньшинству элемент контейнера, нам нужно вызывать эти функции немного по-разному:

std::vector<int> values = { /* больше 10 значений */ };
std::nth_element(values.begin(), values.begin() + 9, values.end());
int tenth_element = values[9];
std::vector<int> values = { /* больше 10 значений */ };
std::partial_sort(values.begin(), values.begin() + 10, values.end());
int tenth_element = values[9];В конечном итоге, после десятков прогонов всех тестов в Google и с помощью удачного ветра случайности мы выявили пару тысяч тестов, которые зависимы от стабильности алгоритмов сортировки и выбора. Поскольку мы также планировали обновить алгоритмы сортировки, этот процесс помог делать это постепенно и надёжно.
В конечном итоге, для исправления всего этого нам понадобилось около года.
Какие сбои вы, вероятно, обнаружите?
Золотые тесты
Во-первых, мы, разумеется, обнаружили множество сбоев в описанных выше золотых тестах, и это было неизбежно. Из мира open source можно посмотреть на ClickHouse22, 23, они тоже решили реализовать описанную выше случайность.

Типичные изменения в золотых тестах
Большинство изменений выглядело именно так — мы создавали правильный порядок и обновляли золотые тесты.
К сожалению, золотые тесты могут быть довольно чувствительными к нагрузкам в продакшене, например, при разворачивании потокового движка — что если некоторые инстансы создают немного отличающиеся результаты для одного и того же шарда? Или что если какой-то алгоритм сжатия случайно использует
std::sort и сравнивает контрольную сумму от другого сервиса, в котором реализация не обновилась? Это может вызвать несовпадение контрольных сумм, повышение количества ошибок, проблемы у пользователей и даже потерю данных, и вы не сможете просто заменить алгоритм, потому что это может неожиданным образом повредить нагрузкам в продакшене. Закон Хайрама во всём своём великолепии. Например, чтобы команды смогли мигрировать, нам пришлось инъецировать в пару мест старые реализации.Ох, чёрт, детерминированность
Некоторые другие изменения могут потребовать перехода от
std::sort к std::stable_sort, если требуется детерминированность. Мы рекомендуем написать комментарий о том, почему это важно, поскольку stable_sort гарантирует, что равные элементы будут в том же порядке, что и до сортировки.
Примечание: параметры по умолчанию в других языках отличаются, и, вероятно, это хорошо
Во многих языках24, в том числе в Python, Java, Rust,
sort() стабильна по умолчанию и, по-моему, это решение лучше. Например, в Rust есть .sort_unstable(), не имеющий гарантий стабильности, но сообщающий об этом явно. Однако у C++ другие приоритеты, например, использование чего-то не должно делать больше, чем требуется (принцип «ты не платишь за то, что не используешь»). По нашим бенчмаркам std::stable_sort была на 10-15% медленнее, чем std::sort, и распределяла линейную память. Учитывая преимущества в производительности, для кода на C++ это было довольно критично. Мне кажется, что по умолчанию Rust предполагает более строгие ограничения с возможностью их смягчить, а C++ предполагаем более мягкие ограничения с возможностью их ужесточения.
Логические баги
Мы нашли множество мест, где пользователи вызывали неопределённое поведение или создавали неэффективность. Перечислим их по степени возрастания важности.
Сортировка двоичных данных
При сравнении булевой переменной, например, когда вы разделяете данные по существованию какого-то параметра, очень привлекательным кажется использование вызова
std::sort.struct Data {
bool has_property;
// …
};
std::vector<Data> data(FillData());
std::sort(data.begin(), data.end(), [](const Data& lhs, const Data& rhs) {
return lhs.has_property < rhs.has_property;
});Однако для функций сравнения, выполняющих сравнение только по булевым переменным, у нас есть гораздо более быстрые линейные алгоритмы
std::partition и его стабильная версия std::stable_partition.struct Data {
bool has_property;
// …
};
std::vector<Data> data(FillData());
/*
Изменяет порядок элементов в интервале [first, last) таким образом,
чтобы все элементы, для которых предикат p возвращает true, предшествовали
элементам, для которых предикат p возвращает false. Относительный порядок
элементов не сохраняется.
*/
std::partition(data.begin(), data.end(), [](const Data& other) {
// Отрицание, поэтому все со свойством переносятся вправо.
return !other.has_property;
});Даже несмотря на то, что современные алгоритмы хорошо справляются с определением кратности, лучше предпочитать
std::partition, хотя бы ради читаемости.Сортировка больше необходимого
Мы часто встречали паттерн sort+resize.
// Нас интересуют только n сущностей с наибольшими score.
std::sort(vector.begin(), vector.end(),
HasHigherScore());
vector.resize(n);Из приведённого выше кода мы можем понять, что несмотря на то, что исследовать нужно каждый элемент, сортировка всего vector (позже
// We only care about the n entities with the highest scores.
std::partial_sort(vector.begin(),
vector.begin() + n,
vector.end(),
HasHigherScore());
vector.resize(n);К сожалению, не существует стабильного аналога
std::partial_sort, поэтому если требуется детерминированность, нужно исправить компаратор.Язык C++ сложен
Если в компараторе используется несоответствующий тип, то C++ не предупредит об этом даже при
-Weverything. На скриншоте ниже при сортировке вектора float с компаратором std::greater<int> не было выдано ни одного предупреждения.
Отсутствие следования строгому слабому упорядочиванию
При вызове в C++ любых функций упорядочивания, в том числе и
std::sort функции сравнения должны соответствовать строгому слабому упорядочиванию, что формально означает следующее:- Нерефлексивность:
ложно
- Асимметрию:
и
не могут одновременно быть истинными
- Транзитивность:
и
подразумевают
- Транзитивность несравнимости:
и
подразумевают
, где
означает, что
и
ложны.
Все эти условия логичны и для оптимизации алгоритмы используют их все. Первые три условия задают строгое частичное упорядочивание, а четвёртое добавляет соотношения эквивалентности для несравнимых элементов.
Как вы могли догадаться, мы столкнулись с нарушением всех условий. Чтобы продемонстрировать их, я ниже покажу скриншоты того, где я их нашёл при помощи Github codesearch (https://cs.github.com). И я не особо старался искать баги, самое важное, что нарушения происходят. После этого мы поговорим о том, как их можно использовать в эксплойтах.
Нарушение нерефлексивности и асимметрии
Под спойлером есть слайдшоу, изучите его.
Слайдшоу








Все они нарушают правило нерефлексивности, а
comp(x, x) возвращает true. Возможно, вы скажете, что это можно не использовать на практике, однако мы получили болезненный урок о том, что даже тесты не всегда помогают.30 и 31 элемент. Правильное исполнение и SIGSEGV
Вы можете помнить, что для количества элементов до 30 для тривиальных типов (и до 6 для нетривиальных) сортировка LLVM/libcxx использует сортировку вставками, а при бОльших количествах возвращается к quicksort. Однако если передать компаратор, в котором не удовлетворяются условия нерефлексивности и асимметрии, то можно обнаружить, что с 31 элементом программа может перейти в segfault, хотя с 30 элементами работает отлично. Рассмотрим пример, в котором мы хотим переместить все отрицательные элементы вправо и отсортировать все положительные, как и в примерах выше.

https://gcc.godbolt.org/z/17r76q7eo
Мы видели, что пользователи пишут тесты для небольших интервалов, однако когда количество элементов растёт,
std::sort может привести к SIGSEGV, а при тестировании это можно упустить; это может стать интересным вектором атаки для вылета программы.Это используется в реализации libcxx, чтобы ждать, когда какое-то условие окажется ложным, ведь мы знаем, что в какой-то момент будем сравнивать два равных элемента:
// Известно, что идущий вверх поиск защищён, но не идущий вниз.
// Дополним идущий вниз поиск защитой.
// __m по-прежнему защищает идущий вверх __i
while (__comp(*__i, *__m))
++__i;Нарушение транзитивности несравнимости

https://webrtc-review.googlesource.com/c/src/+/251681
Мы можем создать пример, где нарушается четвёртое условие.
Худшее, что может случиться в таком случае с текущей реализацией: элементы не будут отсортированы (без segfaults; это требует доказательства, однако статья и так уже слишком длинная), смотрите:

https://gcc.godbolt.org/z/c71qzM97f
И снова, если использовать меньше 7 элементов, применяется сортировка вставками, и нельзя создать контрпример, в котором
std::is_sorted не работает. Хотя теоретически это неопределённое поведение, его очень сложно распознать программами очистки или тестами, и в реальности простые случаи пропускаются.Этот фрагмент может просто выглядеть так:
std::vector<double> vector_of_doubles(FillData());
std::sort(vector_of_doubles.begin(), vector_of_doubles.end());Почему? Потому что double/float могут быть
NaN, что означает x < NaN и NaN < x ложны, а это означает, что x эквивалентно NaN, то есть для каждого конечного x мы имеем x == NaN, но очевидно, что x == NaN и y == NaN не подразумевают x == y.Итак, если у нас есть
NaN в векторе, вызов std::sort в теории приводит к неопределённому поведению. Это часть проблемы, которая описывается в видео:Постойте, но ведь для поиска нарушений строгой слабой упорядоченности требуется кубическое время
Для выявления нарушений строгой слабой упорядоченности нужно проверять все тройки элементов, что требует времени
И мы сделали то, что сделало бы большинство инженеров. Мы решили после рандомизации проверять тройки
У std::nth_element соотношение багов к рандомизации выше всего. И вот почему
Хотя
std::sort использовалась больше всего и было выявлено наибольшее количество сбойных тестовых случаев, мы выяснили, что рандомизация для std::nth_element и std::partial_sort находила больше логических багов на каждый сбойный тестовый случай. Я создал очень простой запрос codesearch, ищущий два близких вызова std::nth_element, и сразу же обнаружил некорректное использование. Сначала попробуйте найти баги самостоятельно (все их можно посмотреть в 25):
Слайдшоу
















Все они следуют одному и тому же паттерну: игнорируют результаты первого вызова
nth_element. Визуализация бага показана на изображении:
И да, это случается достаточно часто, я даже не пытался найти много багов, достаточно было десять минут исследовать результаты github codesearch. Исправить их легко, достаточно получать доступ к
nth элементу только после выполнения вызова. Будьте аккуратны.Как найти плохие вызовы сортировки среди сотен мест в вашей кодовой базе?
Даже в небольших репозиториях пользователи вызывают
std::sort в десятках, сотнях, а то и тысячах разных мест. Как же найти вызовы сортировки, создающие плохое поведение? Иногда они очевидны, иногда совершенно нет, и исследование — это отдельная задача, сильно упрощающая процесс отладки.Мы использовали inline-переменные26 (иногда люди, занимающиеся компиляторами, называют их weak symbols) C++, которые можно объявлять в заголовках и задавать в любом месте без ошибок компоновки.
// В <algorithm>
// Объявляем inline-переменную.
extern void (*ExtremelyHackyCallThatYouWillNotOverride)()
__attribute__((weak)) = nullptr;
// …
// До вызова сортировки
// …
if (ExtremelyHackyCallThatYouWillNotOverride)
ExtremelyHackyCallThatYouWillNotOverride();
_VSTD::__sort<_Comp_ref>(_VSTD::__unwrap_iter(__first), _VSTD::__unwrap_iter(__last), _Comp_ref(__comp));
// …
// main.cpp
#include <algorithm>
// Выводит трассировку стека.
void backtrace_dumper();
int main(int argc, char** argv) {
ExtremelyHackyCallThatYouWillNotOverride = &backtrace_dumper;
return InvokeRealMain(argc, argv);
}Это помогло найти все трассировки стеков вызовов
std::sort и провести статистический анализ того, откуда они пришли. Для этого всё равно требуется человеческое участие, но это сильно упрощает процесс отладки.Примечание об очень небольшой опасности
Если функция
backtrace_dumper каким-то образом использует std::sort, то вы можете попасть в бесконечную рекурсию. Этот способ не сработал с первого раза, поскольку в Google мы используем аллокатор TCMalloc, а он применяет std::sort.
https://github.com/google/tcmalloc/blob/2bac28c802ce5e93b284803854417cfe6dde0fff/tcmalloc/huge_page_filler.h#L1414
То же самое произошло с
absl::Mutex. Было очень «весело» выяснять, почему завершаются сбоями не связанные друг с другом тесты.Также стоит заметить, что
backtrace_dumper, скорее всего, должна быть потокобезопасной.Небольшая автоматизация процесса
Иногда можно сделать так:
- Найти все вызовы
std::sortчерез этот поиск обратной трассировки - Заменять их один за другим на
std::stable_sort - Если тесты становятся зелёными, сообщить пользователю, какой вызов, скорее всего, виноват в проблемах
- Может быть, предложить заменить его на
std::stable_sort- Принять патч иногда проще, чем делегировать устранение проблемы команде или человеку
- Если ничего не найдено, отправить баг или изучить код вручную
Это ускорило процесс, и некоторые команды решили использовать
std::stable_sort, осознавая связанное с этим снижение производительности, а другие поняли, что что-то не так, и попросили другое исправление.Глава 3. Какую сортировку мы заменяем?
В каком-то смысле, это самое маловажное и это не требует такого одновременного внимания и усилий большого количества людей. Если кто-то решит изменить реализацию с приведённой выше рандомизацией, то легче будет подготовиться, выполнить переход и получать удовольствие от экономии (вместе с преимуществами устранения серьёзных багов). Однако изначальной целью нашего проекта было повышение производительности, поэтому нужно немного рассказать об этом.
Также стоит признать, что споры о самой быстрой сортировке никогда не утихнут и тем не менее нам стоит стремиться двигаться к более совершенным алгоритмам. Не буду утверждать, что наш выбор самый лучший, он просто существенно улучшает статус-кво благодаря множеству потрясающих идей.
Примечание о распространении
Мы выяснили, что важно оптимизировать оба случая, от сортировки integer, где сравнения очень малозатратны, до чрезвычайно тяжёлых нагрузок, где сравниваются функции или даже выполняется декомпрессия кодеками. И как говорилось выше, очень важно выявить паттерны.
Ошибочные предсказания ветвлений для малозатратных сравнений
// *__m - это median. partition [__first, __m) < *__m и
// *__m <= [__m, __last)
//
// Особая обработка для почти отсортированных целевых данных
while (true) {
while (__comp(*++__i, *__m));
while (!__comp(*–__j, *__m));
if (__i > __j) break;
swap(*__i, *__j);
}
swap(*__i, *__m);В текущей реализации сортировка выполняет значительное количество команд ветвления при разделении входных данных относительно опорного элемента. Ветвления показаны выше, от их результатов зависит, нужно ли выполнять цикл. Эти ветвления довольно сложно предсказывать, особенно в случаях, когда опорный элемент выбран ровно в середине (например, в случайных массивах). Ошибочно предсказанные ветвления приводят к сбросу всего конвейера обработки и обычно считаются вредящими исполнению. Это достаточно хорошо известный и тщательно изученный вопрос28, 29. Иногда лучше выбрать сдвинутый опорный элемент, чтобы избежать такого большого количества циклов.

Как ошибочные предсказания ветвления влияют на Quicksort29
Чтобы справиться с этим, мы используем технику, описанную в BlockQuickSort28.
BlockQuickSort стремится избежать большинства ветвлений благодаря отделению перемещения данных от операции сравнения. Это реализуется созданием двух буферов размера B, в которых хранятся результаты сравнения (например, можно выбрать B=64 и хранить только 64-битные integer), один для левой половины, а другой для правой при обходе блоков размера B. В отличие от приведённой выше реализации, он не добавляет никакого ветвления и если сделать всё правильно, компилятор генерирует хороший SIMD-код с 16-байтными или 32-байтными командами
pcmpgt/pand/por для кода SSE4.2 и AVX2.
https://godbolt.org/z/nrhT88MsM
То же самое относится и к ARM.

https://godbolt.org/z/W6sjrMnWf
После заполнения всех буферов мы должны менять их местами относительно опорного элемента. К счастью, для этого достаточно найти индексы элементов, которые нужно обменять местами следующими. Так как буферы находятся в регистрах, мы используем команды
ctz (count trailing zeros, в x86 bsf (Bit Scan Forward) или tzcnt (появилась в BMI)), blsr (Reset Lowest Set Bit, появилась в BMI) для поиска индексов для элементов, избегая таким образом всех команд ветвления.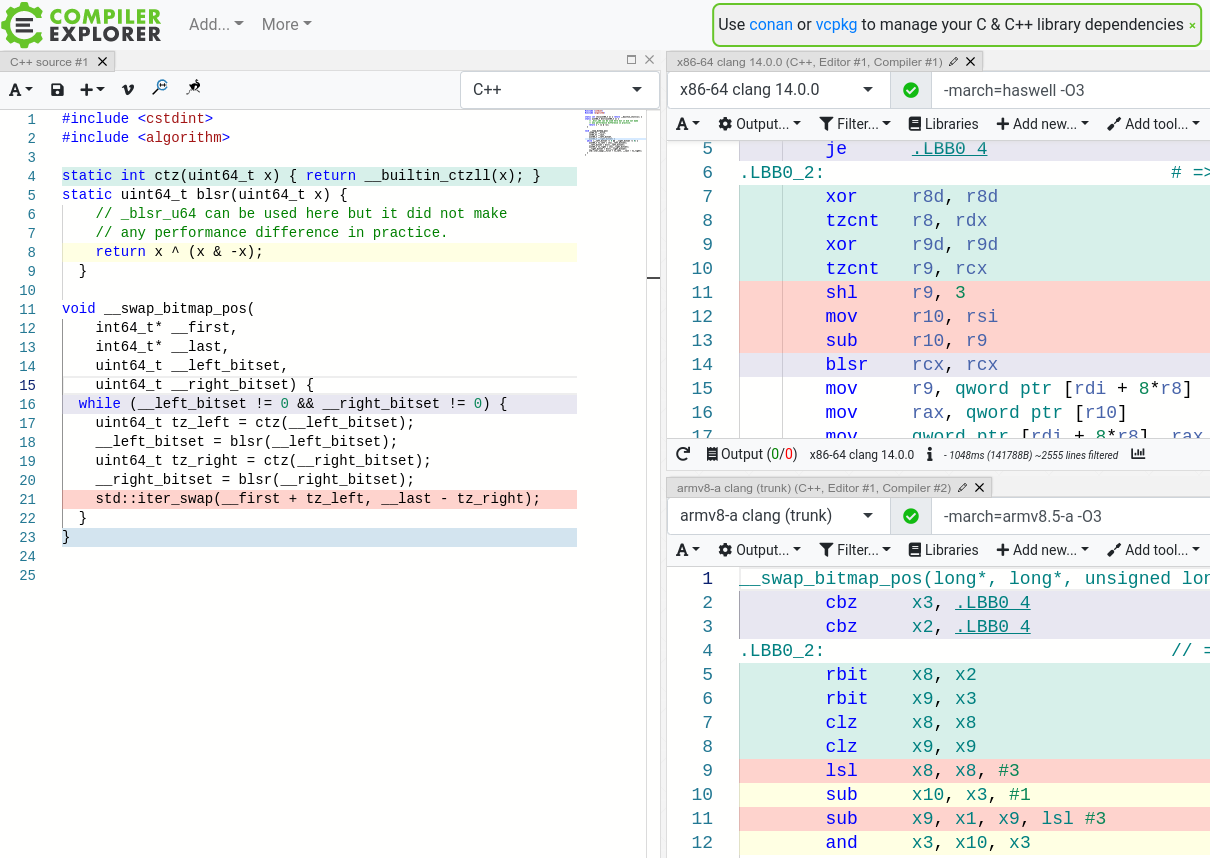
https://godbolt.org/z/YPTWT4exz. Стоит заметить, что у aarch64 нет аналога blsr
Бенчмарки демонстрируют при сортировке случайных перестановок integer экономию примерно на 50%. Можно изучить их в https://reviews.llvm.org/D122780.
Тяжёлые сравнения
Так как мы устранили ошибочно предсказываемые ветвления, теперь логичнее взять другие эвристики, например, выбор опорного элемента.
// Используем технику ninther Таки или медиану 3 для выбора опорного элемента.
// Получаем медиану из 3 медиан 9 элементов
// (first, first + half, last – 1)
// (first + 1, first + half – 1, last – 2)
// (first + 2, first + half + 1, last – 3)
_VSTD::__sort3<_Compare>(__first,
__first + __half_len,
__last – difference_type(1),
__comp);
_VSTD::__sort3<_Compare>(__first + difference_type(1),
__first + (__half_len – 1),
__last – difference_type(2),
__comp);
_VSTD::__sort3<_Compare>(__first + difference_type(2),
__first + (__half_len + 1),
__last – difference_type(3),
__comp);
_VSTD::__sort3<_Compare>(__first + (__half_len – 1),
__first + __half_len,
__first + (__half_len + 1),
__comp);
_VSTD::iter_swap(__first, __first + __half_len);Интуитивно понятно, что хороший опорный элемент уменьшает количество сравнений, но увеличивает количество ошибочных предсказаний ветвления. Если мы решим вторую проблему, то сможем справиться и с первой. Чем больше элементов на роль опорного элемента мы рассмотрим в случайных массивах, тем меньше сравнений мы будем делать в конце.
Прочие небольшие оптимизации включают в себя неохраняемую сортировку вставками для не самых левых интервалов во время рекурсии (из всех интервалов на каждом уровне рекурсии есть только один самый левый). Все они дают небольшие, но надёжные преимущества.
Всё это согласуется с реализацией pdqsort3, которую довольно часто используют в качестве реализации и в других языках. И мы наблюдаем улучшения примерно на 20-30% для случайных данных, не жертвуя при этом производительностью при почти отсортированных паттернов.
Обучение с подкреплением для небольших сортировок
Ещё одно реализованное изменение внесло инновации в генерации ассемблерного кода для небольших сортировок, в том числе
cmov (команда условного перемещения). Это изменение https://reviews.llvm.org/D118029. Что произошло?Из раздела «История LLVM продолжается» вы можете помнить функции sort4 и sort5. В них есть ветвление, однако существуют и другие способы сортировки элементов: сети сортировки. Это сети, абстрагирующие устройства, составленные из фиксированного количества «линий», передающих значения, и модулей компараторов, соединяющих пары линий, которые обменивают местами значения в линиях, если они находятся не в нужном порядке. Оптимальные сети сортировки — это сети, сортирующие массив наименьшим количеством операций сравнения и обмена местами (compare-and-swap). Для трёх элементов нужно выполнить операцию три раза, для четырёх элементов — пять раз, а оптимальная сеть сортировки для пяти элементов состоит из девяти операций compare-and-swap.
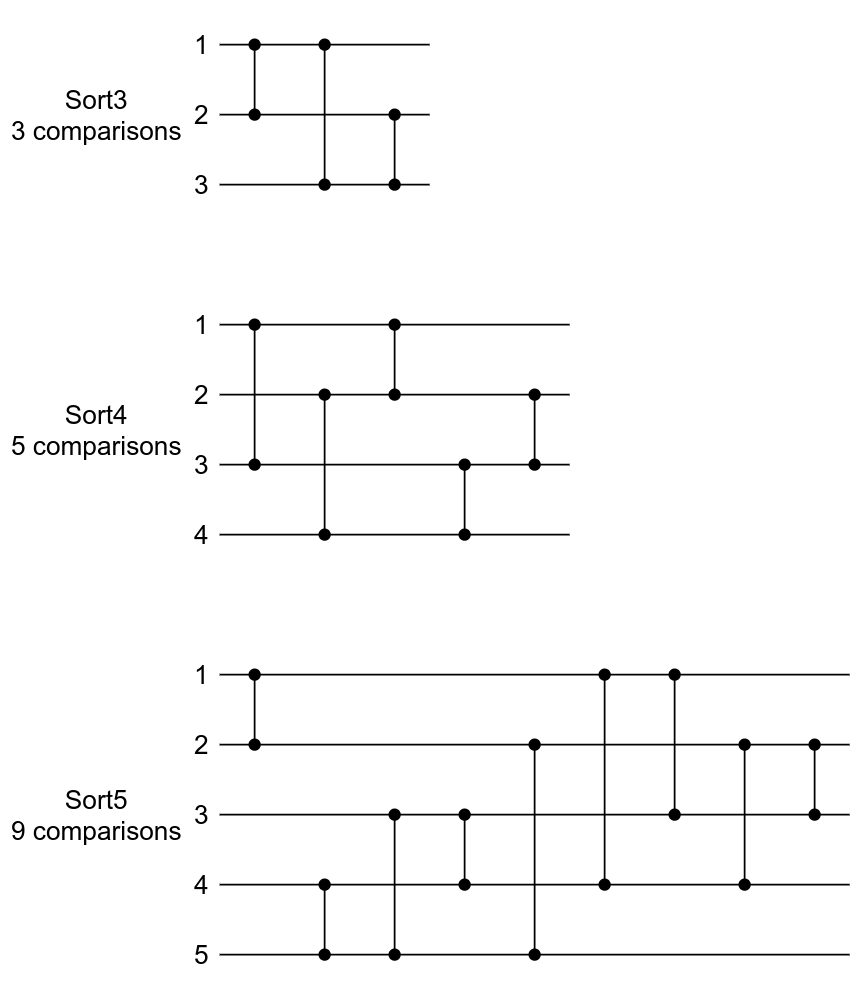
Оптимальные сети для больших значений по-прежнему под вопросом, но о том, как опровергнуть гипотезу оптимальных сетей для 11 и 12 элементов, вы можете прочитать в потрясающем посте Proving 50-Year-Old Sorting Networks Optimal30 Дженнис Хардер.
В ассемблерном коде x86 и ARM есть команды
cmov reg1, reg2 и csel reg1, reg2, flag, которые перемещают или выбирают регистры на основании значения сравнений. Их можно активно использовать для операций compare-and-swap.
https://gcc.godbolt.org/z/eG1EnqdTa
А для обмена местами
-
загрузок из указателей,
сохранений в указатели
- Для каждой команды сравнения
cmpвыполнятьmovдля временного регистра и дваcmovдля обмена местами. Всегокоманд.
Итого мы имеем:
- Sort2 — 8 команд (2 элемента и 1 сравнение)
- Sort3 — 18 команд (3 элемента и 3 сравнения)
- Sort4 — 28 команд (4 элемента и 5 сравнений)
- Sort5 — 46 команд (5 элементов и 9 сравнений)

Ровно 18 команд для sort3 с 64-битными integer, по 1 для имени и 1 для команды возврата
Однако как мы видим из показанного выше обзора, sort3 написана немного иначе, с одним условным обменом и с магическим обменом.
// Гарантирует, что *__x, *__y и *__z упорядочены согласно компаратору __c,
// при допущении, что *__y и *__z уже отсортированы.
template <class _Compare, class _RandomAccessIterator>
inline void __partially_sorted_swap(_RandomAccessIterator __x, _RandomAccessIterator __y,
_RandomAccessIterator __z, _Compare __c) {
using value_type = typename iterator_traits<_RandomAccessIterator>::value_type;
bool __r = __c(*__z, *__x);
value_type __tmp = __r ? *__z : *__x;
*__z = __r ? *__x : *__z;
__r = __c(__tmp, *__y);
*__x = __r ? *__x : *__y;
}
template <class _Compare, class _RandomAccessIterator>
inline void __sort3(_RandomAccessIterator __x1, _RandomAccessIterator __x2,
_RandomAccessIterator __x3, _Compare __c) {
_VSTD::__cond_swap<_Compare>(__x2, __x3, __c);
_VSTD::__partially_sorted_swap<_Compare>(__x1, __x2, __x3, __c);
}Если вставить это в Godbolt, то мы увидим, что такой код создаёт на одну команду меньше. 19-я строка слева стала 16-ой справа, а 15-я строка слева полностью исчезла.

https://gcc.godbolt.org/z/59TMfhs6v
Думаю, именно об этом говорят авторы обучения с подкреплением в патче. Генерация помогла найти возможность, выяснив, что если в тройке (X, Y, Z) последние два элемента (Y <= Z) отсортированы, задачу лучше выполнить за 7 команд, чем за 8.
- Перемещаем Z в tmp.
- Сравниваем X и Z.
- Выполняем условный перенос X в Z.
- Выполняем условный перенос X в tmp
-
Перемещаем tmp в X.— этот этап устранён - Сравниваем tmp и Y.
- Выполняем условный перенос Y в X.
- Выполняем условный перенос tmp в Y.
Для сортировки четырёх integer нет оптимальной сети с такой парой сравнений, но для сортировки пяти может быть до трёх пар. В конечном итоге патч позволил узнать, как экономить 1 команду в каждом красном кружке ниже. Это те пары линий, в которых 2 элемента уже отсортированы.

Это позволило уменьшить количество команд в небольших случаях 18->17 при сравнении трёх integer и 46->43 при сравнении пяти integer. Возникает вопрос: чтобы минимизировать количество команд, нам хочется создать такие сети с наибольшим количеством подобных магических обменов.
Действительно ли они быстрее? В случае 18->17 это не всегда так, поскольку убранная команда
mov хорошо встроена в конвейер. Фронтенду процессора всё равно остаётся меньше работы по декодированию команды, но, вероятно, в бенчмарках этого не будет заметно. Для 46->43 ситуация такая же.
Sort3 с 18 и с 17 командами: https://quick-bench.com/q/0THJhOe5q2-vQsEy4v5DrAFGzBc. Информацию по сравнению Sort5 с 46 и 43 командами см. в https://quick-bench.com/q/NXRFUJdHUoG6KMFSQ9B3fiVSKZ4
В ревью LLVM отмечается, что удаётся сэкономить примерно 2-3% для бенчмарков с integer, но экономия в основном связана с переходом от версии с ветвлением к версии без ветвления. Уменьшение количества команд особо не помогает, но это всё равно хороший пример того, как машинное обучение может стимулировать оптимизации компиляторов в таких примитивах, как сети сортировки, а также в генерации ассемблерного кода. Я крайне рекомендую всем любителям C++ изучить патч, в нём есть множество интересных идей и сложных обсуждений того, как их правильно реализовать31.
Заключение
Как вы можете помочь?
Предстоит сделать ещё многое. Вот краткий список того, с чем вы можете помочь:
- Реализовать описанную выше рандомизацию в отладочных режимах
- Это можно сделать для библиотеки GNU library, Microsoft STL, других языков наподобие Rust, D, и т. п.
- Добавить отладочные проверки строгого слабого упорядочивания во всех функциях, которые этого требуют.
-
std::sort, std::partial_sort, std::nth_element, std::min_element, std::max_element, std::stable_sortи в других, во всех стандартных библиотеках. Во всех языках наподобие Rust, Java, Python, D, и т. д. Как мы говорили, похоже, вполне достаточно проверять не более 20 элементов на вызов. Также при необходимости можно добавить сэмплирование.
-
- В своём проекте на C++ попробовать добавить отладочный режим, устанавливающий какой-то уровень
_LIBCPP_DEBUG27. - Рассмотреть возможность рандомизации для тех API, на которые можно положиться как минимум в режиме тестирования/отладки. По-другому создавать seed хэш-функции, чтобы не полагаться на порядок итерации хэш-таблиц. Если функция должна быть только ассоциативной, попробовать накапливать результаты в другом порядке, и т. д.
- Исправить наихудший случай
std::nth_elementво всех реализациях стандартных библиотек. - Ещё сильнее оптимизировать генерацию ассемблерного кода для сортировок. Как видите, тут тоже есть пространство для оптимизаций!
Последние мысли
Когда мы начали этот процесс более года назад (разумеется, работали над ним не полный рабочий день), первой основной целью была производительность. Однако проблема оказалась гораздо более сложной. Мы выявили несколько сотен багов (в том числе довольно критических). В конечном итоге мы нашли способ предотвратить появление багов в будущем, что поможет нам применять корректные реализации и, например, сразу же видеть преимущества без помех в виде поломанных тестов. Если ваша кодовая база велика, то используйте флаг сборки из libcxx и подготовьтесь к миграции. Самое важное в этом проекте было то, что мы получили опыт изменения даже простейших вещей в большом масштабе и научились бороться с законом Хайрама. Я рад, что участвовал в нём и помогал команде open source учиться на нём.
Благодарности
Благодарю Нилая Ваиша, запушившего изменения для новой сортировки в LLVM, мейнтейнера libcxx Луиса Дионне за терпеливое согласование наших изменений. Благодарю Morwenn за выдающуюся работу по сортировке, которая меня многому научила5. Спасибо Орсону Питерсу и pdqsort, которая сильно повысила производительность современной сортировки в памяти.
Ссылки
- В знаменитом учебнике Кормена и соавторов Introduction to Algorithms более пятидесяти страниц посвящено алгоритмам сортировки.
- Ani Kristo, Kapil Vaidya, Ugur Çetintemel, Sanchit Misra, and Tim Kraska. 2020. The Case for a Learned Sorting Algorithm. SIGMOD ’20.
- Hackernews: “I think it’s fair to say that pdqsort (pattern-defeating quicksort) is overall the best”
- In-place Parallel Super Scalar Samplesort (IPS4o)
- https://github.com/Morwenn/cpp-sort — коллекция самых интересных и эффективных алгоритмов, написанных на C++
- libc++: A Standard Library for C++0x, Howard Hinnant, 2010 LLVM Developers’ Meeting
- Один из самых популярных вызовов сортировки в ListFieldsMayFailOnStripped Google
- H. Mannila, “Measures of Presortedness and Optimal Sorting Algorithms,” in IEEE Transactions on Computers, vol. C-34, no. 4, pp. 318-325, April 1985, doi: 10.1109/TC.1985.5009382.
- C++ Standard Library
- Original std::sort implementation by Stepanov and Lee
- Antiquicksort: https://www.cs.dartmouth.edu/~doug/aqsort.c
- Quickselect
- nth_element worst case fallback in GNU libstdc++
- Fast Deterministic Selection by Andrei Alexandrescu
- Introsort
- Median of medians
- [libc++] Introsort based sorting function (2017, unsubmitted)
- libc++ has quadratic std::sort (reddit discussion)
- Add introsort to avoid O(n^2) behavior and a benchmark for adversarial quick sort input (submitted).
- [libcxx][RFC] Unspecified behavior randomization in libcxx
- ASLR (address space layout randomization)
- Sort added equal items ranges randomization (ClickHouse)
- bitsetsort peformance check (ClickHouse)
- Sort stability defaults in different programming languages
- All found open source issues (slides with repo names, commits and files)
- Inline variables in C++
- Debug mode in libcxx
- Stefan Edelkamp and Armin Weiß. 2019. BlockQuicksort: Avoiding Branch Mispredictions in Quicksort. ACM J. Exp. Algorithmics 24, Article 1.4 (2019), 22 pages. DOI.
- Kaligosi, K., & Sanders, P. (2006). How Branch Mispredictions Affect Quicksort. Algorithms – ESA 2006, 780–791. doi:10.1007/11841036_69
- Proving 50-Year-Old Sorting Networks Optimal
- Introduce branchless sorting functions for sort3, sort4 and sort5 (LLVM review)
Комментарии (5)

roger_h
25.04.2022 18:37+3С тексте проблема с формулами, типа $inline$2 \cdot n \cdot \log_2 n$inline$, читать так трудновато.
Можете поправить?

0xd34df00d
27.04.2022 06:29Добавить отладочные проверки строгого слабого упорядочивания во всех функциях, которые этого требуют.
Чего только люди не придумают, лишь бы не доказывать вещи про код.


ap1973
Жаль, что перевод. Интересно было бы узнать проводилось ли сравнение с TimSort на их наборах данных, и каковы результаты.
myxo
Автор ведет тг канал на русском, можно попробовать там в комментариях спросить — t.me/experimentalchill
upd. Ну и на самом сайте, как я погляжу, можно оставлять комментарии.