В этом посте я возвращаюсь к том, к чему не собирался возвращаться — уменьшению размерности и сжатию полного набора текстур материала (в отличие от единичных текстур) — крайне неисследованной области.

В одном из моих предыдущих постов я описал как простейшая линейная корреляция может быть использована для значительного уменьшения размерности набора текстур материала, а в другом посте рискнул пойти дальше в увлекательную область словарей и разреженного сжатия.

В этот раз я опишу как мы можем оставить мир простых линейных корреляций (который мы исследовали, используя SVD) и использовать техники основанные на данных (машинное обучение!) для изучения нелинейных функций, используя дифференцируемое программирование / нейронные сети.

Я собираюсь рассмотреть:

• Использование нелинейного декодирования попиксельных данных для лучшего уменьшения размерности, чем у линейной корреляции/PCA.

• Расширение нелинейных декодеров с помощью информации о соседних пикселях для улучшения качества реконструкции.

• Использование нелинейных энкодеров на данных SVD для целевой платформы или масштабирования производительности.

• Возможность использования обученных энкодеров/декодеров для данных G-buffer’а.

Заметка: Тут нет ничего магического или “нейронного” (и конечно никакого проклятого ИИ!). Это просто нелинейные отношения и я абсолютно ненавижу эти названия.

С другой стороны, мы будем использовать нейронные сети, так что инвесторы, обратите внимание!

Вдохновение

Недавно появилось несколько статей, которые изменили моё представление об уменьшении размерности для представления материалов.

Я не буду здесь их все перечислять, но тут (а также тут или тут) наиболее недавние, которые выделяются и я могу вспомнить не задумываясь. Вещь, которая показалась мне интересной, необычной и оригинальной — это концепция “нейронного отложенного рендеринга”. Суть в том чтобы иметь компактные латентные коды, которые используются для аппроксимации функций вроде ДФОС (Двулучевой функции отражательной способности) (или даже для финального направленного излучения пикселя) расширенных крошечными нейронными сетями, часто в форме многослойного перцептрона.

А что если мы будем использовать это в полу-офлайн режиме?

Что если мы будем использовать маленькую нейронную сеть для декодирования материалов?

Чтобы объяснить почему я думал, что это может быть интересным, озаботиться использованием “расточительных” нейронок (нейронки всегда расточительны, даже крошечные!), начнём с аппроксимаций функций и настройки нелинейных зависимостей.

Линейные и нелинейные зависимости

В своем посте про SVD и PCA, я рассмотрел как работает линейная корреляция и как её можно использовать. Если вы не читали этот пост, то рекомендую приостановить чтение текущего, так как я собираюсь использовать ту же терминологию и постановку проблемы и пройдусь по ним крайне поверхностно.

Это чрезвычайно мощные методы. И они так хорошо работают поскольку многие проблемы линейны при достаточно большом увеличении. Этот принцип лежит в основе аппроксимаций рядами Тейлора. Локальные уравнения прямых правят инженерным миром! (И они часто могут быть использованы как более подходящая замена билатеральному фильтру).

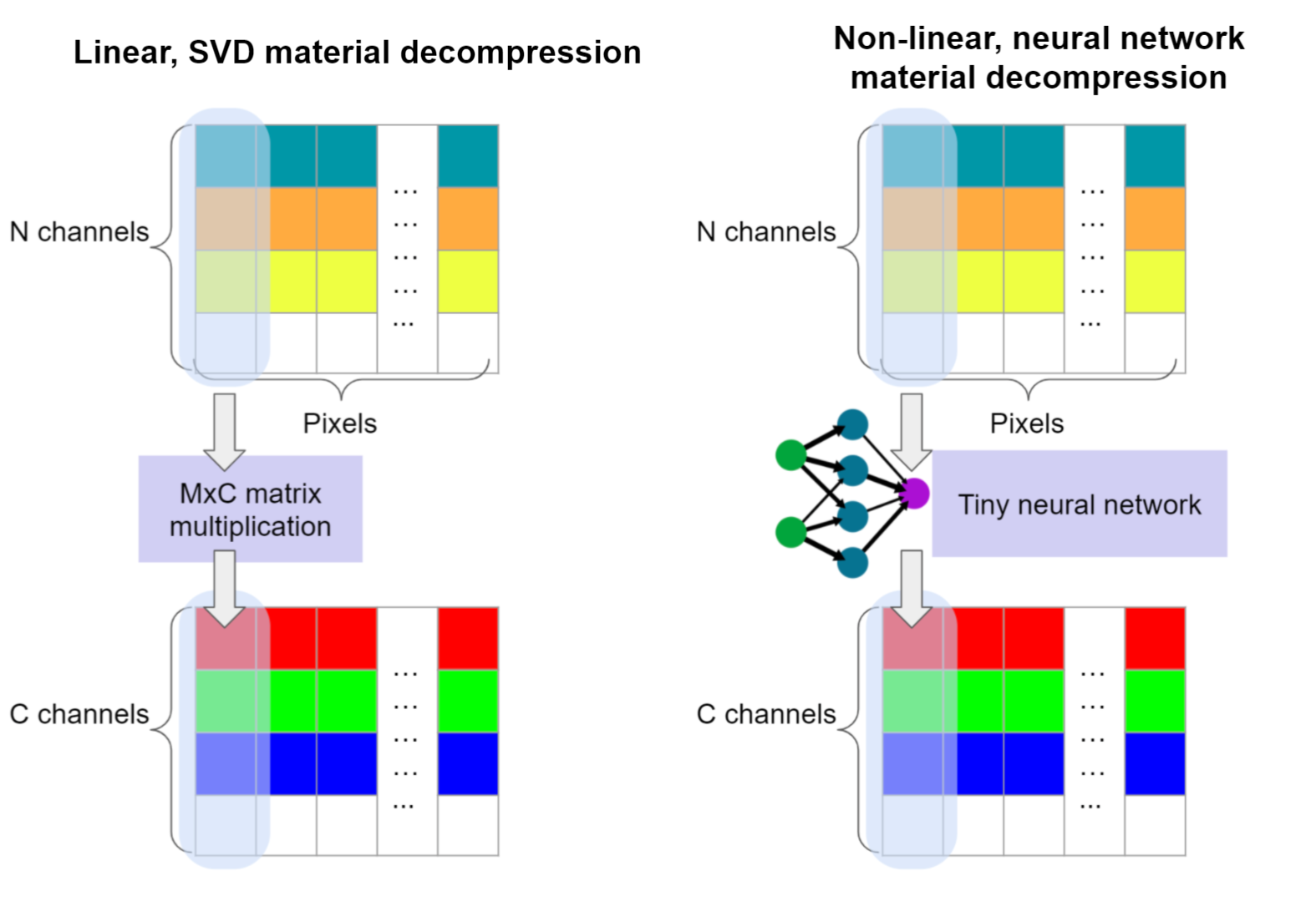
Таким образом, в случае сжатия материалов методом PCA, мы предполагаем линейную зависимость между свойствами материала и цветовыми каналами и используем это чтобы декоррелировать входные данные. Таким образом, мы можем игнорировать компоненты, которые меньше коррелируют и вносят меньший вклад, уменьшая тем самым представление материала и храня небольшое число каналов.

Затем, выходные значения могут быть получены как результат вычисления взвешенной суммы.

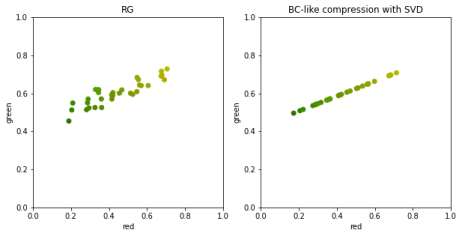
К сожалению, при уменьшении масштаба локальных аппроксимаций (или просто при рассмотрении данных, более приближенных к реальным), зависимости в данных перестают быть линейными.

Часто PCA не достаточно. Так в примере выше мы выкидываем много полезных различий между некоторыми точками.

Но давайте сделаем шаг назад и посмотрим на другой набор простых наблюдений (представленных как зашумленные данные на плоскости XY):

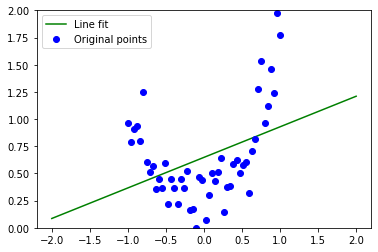
Линейная корреляция не может представить большую часть формы распределения и имеет очень много потерь. Мы можем понять почему — потому что перед нами старая добрая парабола, квадратичная функция.

Приближения линией недостаточно и ошибки велики как внутри распределения, так и на его концах.

Это то, что привело к развитию алгоритмов машинного обучения (PCA определенно тоже алгоритм машинного обучения!) — изучение, объяснение и аппроксимация растущих более сложных зависимостей, как параметрических (где мы подразумеваем некоторую модель реальности и пытаемся подобрать для неё параметры), так и непараметрических (где мы не создаём модель реальности или распределение данных) моделей.

Цель машинного обучения — дать разумный ответ там, где мы сами не знаем ответа, когда у нас нет достаточно точной модели реальности, размерности слишком большие, зависимости слишком сложные, или мы знаем, что они могут меняться.

В таких случаях мы можем использовать множество алгоритмов, но самые модные “очевидно” нейронные сети. :)  В следующем разделе мы рассмотрим почему, но сейчас давайте аппроксимируем наши данные маленьким многослойным перцептроном с тремя нейронами на скрытом слое и функцией активации ReLU (ReLU — это модное название для max(x, 0) — возможно наиболее простая нелинейная функция, подходящая нам и дифференцируемая почти везде!):

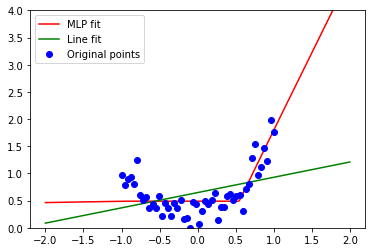
Или например 4 нейрона:

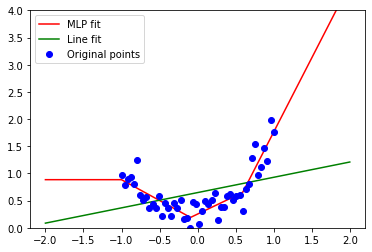
Если нам “улыбнётся удача” (хорошая инициализация), мы можем получить следующее приближение:

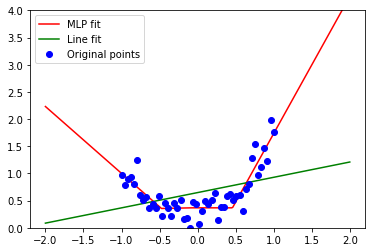
Это не “идеально”, но намного лучше чем линейные модели. SVD, PCA или линейное приближение в классическом виде могут работать только с линейными зависимостями, в то время как нейросети покрывают все остальные интересные и нелинейные.

И поэтому мы будем их использовать!

Отступление — почему многослойный перцептрон, ReLU и нейронные сети такие популярные?

Немного слов о выбранной “архитектуре”. Мы собираемся использовать наиболее олдскульный классический нейросетевой алгоритм — многослойный перцептрон.

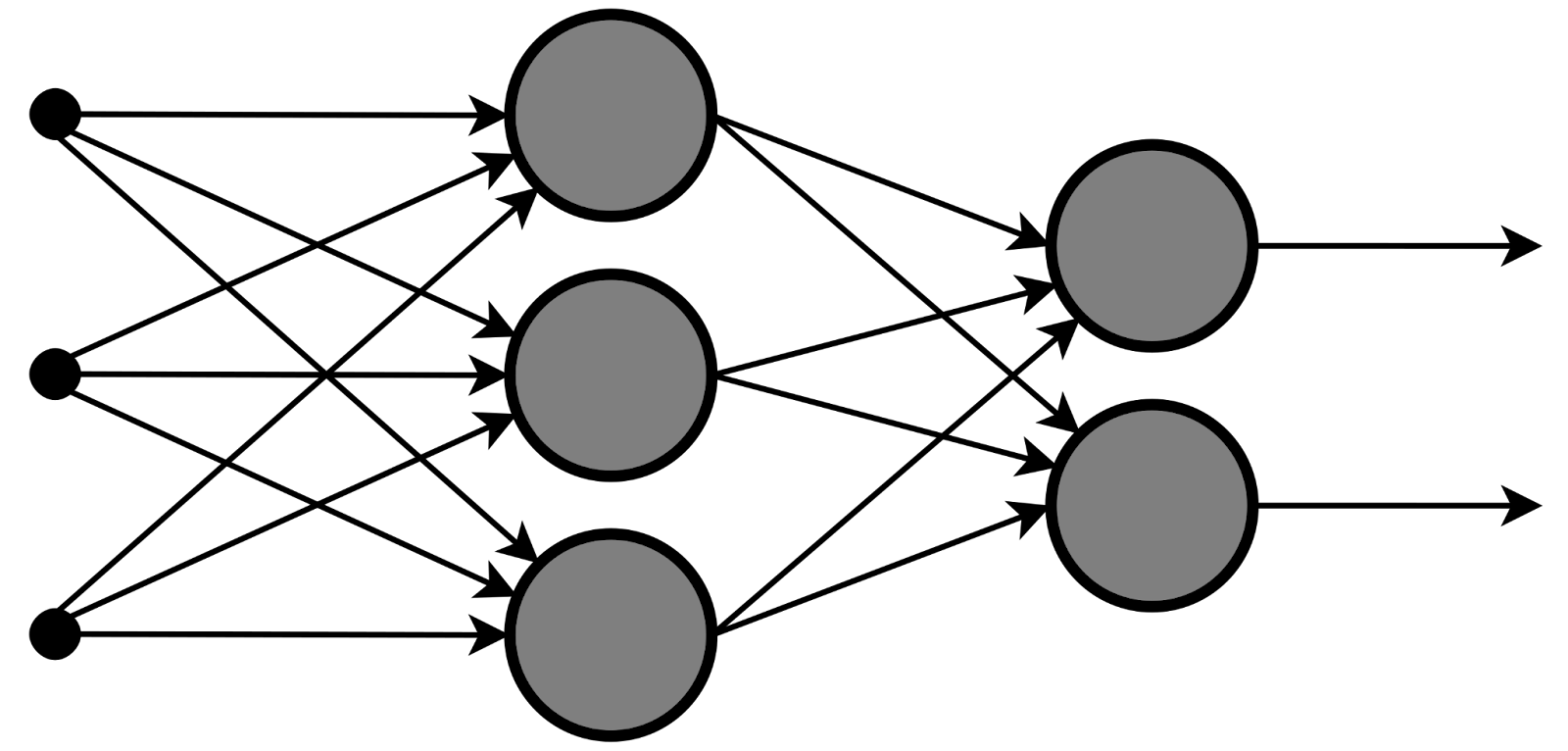
Когда я впервые услышал о “Нейронных сетях” в колледже в середине нулевых на вводном курсе, “нейронные сети” почти всегда были только многослойными перцептронами и были признаны устаревшими. Также я ознакомился со сверточными сетями и реализовал одну из них для моего выпускного проекта. Но они считались медленными, не практичными и обычно работали хуже чем SVM и другие техники. Забавно, как всё изменилось :)

Почему нейронные сети используются сейчас повсеместно?

Есть многочисленные объяснения, от теоретических, об “универсальной аппроксимирующей функции”, до связанных с аппаратным обеспечением (эффективно выполняются на GPU, но так же есть и специальные ускорители сделанные для нейросетей). Но для меня наиболее прагматичное, и возможно немного циничное, зацикленное объяснение: эта область очень “горячая” и как следствие а) актуальные исследования приводят к созданию прекрасных инструментов и библиотек, плюс б) есть множество ноу-хау.

Очень просто использовать нейронные сети для решения проблем, когда у вас есть “какие-то” данные. Существующие библиотеки и инструменты для этого прекрасны и за последнее десятилетие исследований (базирующихся на полвека фундаментальных исследований до этого!) они стали быстрыми и понятными.

Многослойный перцептрон с функцией активации ReLU представляет линейно-кусочную аппроксимацию для решения задачи. В нашем примере, им никогда не получится выразить параболу, но при наличии достаточного количества данных можно будет достаточно хорошо приблизить похожие данные.

Конечно, не имеет смысла использовать нейросети для данных, которые могут быть описаны простой параболой (потому что мы можем использовать параметрическую модель, более точную и эффективную), но если мы работаем с более чем 3-мя измерениями или несколькими сотнями примеров, человеческие размышления и интуиция начинают ошибаться.

Объем пространства возможных решений увеличивается экспоненциально (“проклятие размерности”). В качестве примера рассмотрим следующее (нейронная декомпрессия текстур), мы не можем просто быстро взглянуть на данные и понять “ок, здесь кубическое соотношение в скрытом пространстве между альбедо и глянцевостью”, поэтому найти такое с помощью маленького перцептрона кажется хорошей альтернативой.

Но в этом случае очень просто переобучиться (это помешает исследованию настоящих зависимостей в данных). Например, увеличив количество скрытых нейронов мы получим:

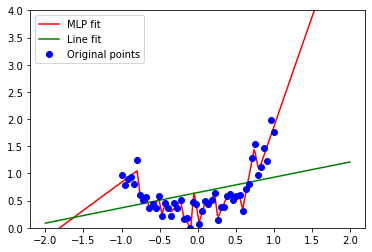
К счастью, для нашего примера это не важно. Для сжатия данных, чем больше переобучение, тем лучше.

Нелинейные соотношения в текстурах

В примере с SVD сжатием мы рассматривали N входных каналов (хранящихся в текстурах) и K (9 в рассматриваемом примере) выходных каналов, где каждый выходной канал вычисляется как x_0 * w_0 + … + x_n-1 * w_n-1, то есть как линейная комбинация.

Давайте ещё раз взглянем на N выходных и K выходных каналов, но теперь между ними будет 64 нейрона одного скрытого слоя с операцией ReLU:

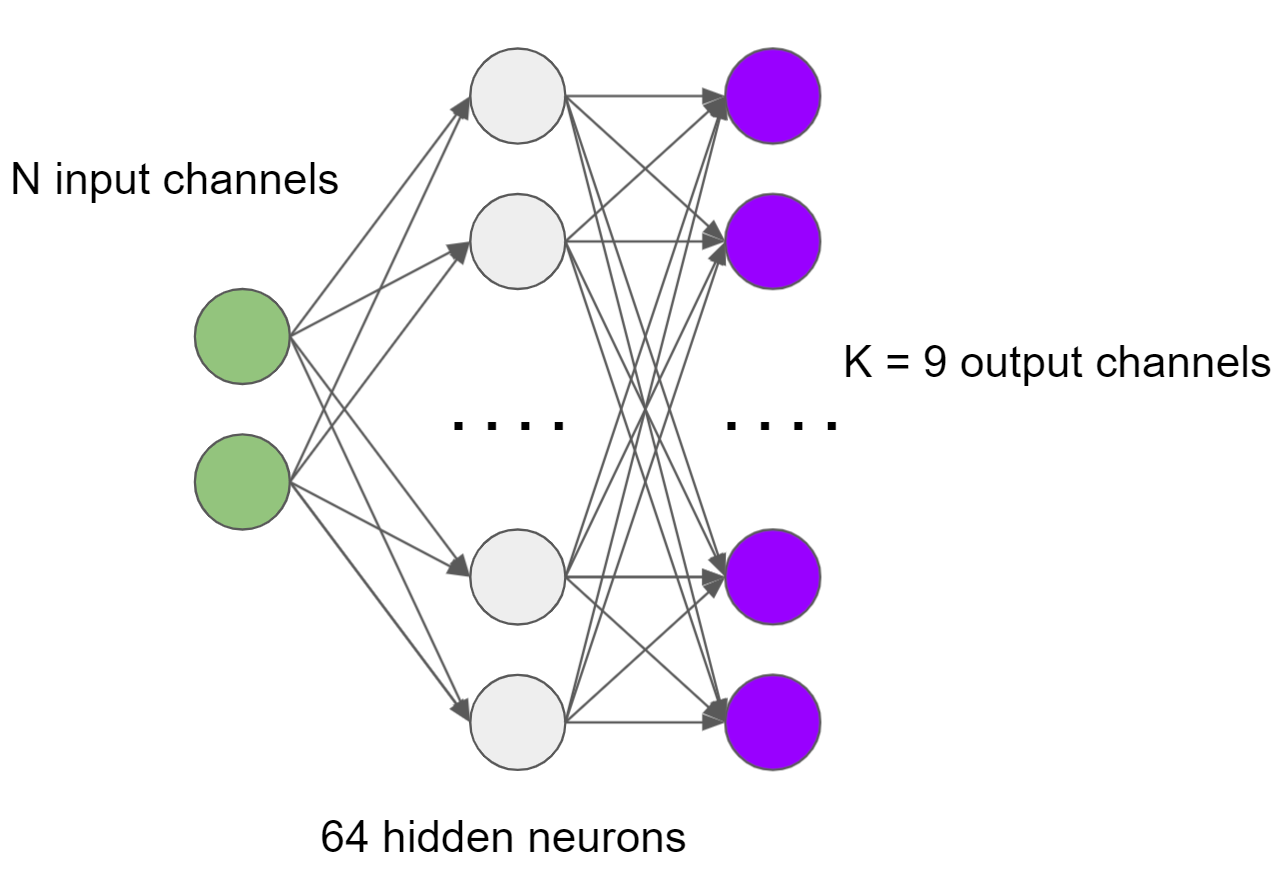
В данном случае, мы выполняем матричное умножение (или последовательность multiply-add инструкций) для каждого нейрона скрытого слоя и используем эти промежуточные значения как “временные” входные каналы и выполняем для них матричное умножение дающее выходные значения.

Это не сверточная нейросеть. Мы по прежнему используем “локальные” данные, читаем то же самое количество информации на канал. В процессе обучения мы обучаем как нейронную сеть, так и входные данные сжатых текстур.

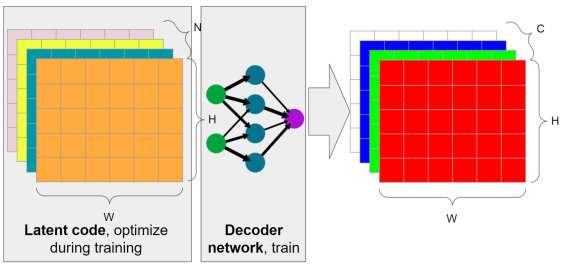
Если данные термины мало о чём вам говорят, к сожалению, я не буду углубляться в обучение сетей, что такое оптимизаторы и скорость обучения (я использовал ADAM с learning rate 0.01). Есть люди, которые гораздо более компетентны в данных вопросах и могу объяснить их лучше. Я учился по книге Deep Learning и могу рекомендовать её, как хороший источник как теории, так и практики, но со времени изучения мной прошло некоторое время и, возможно, сейчас есть лучшие ресурсы.

Однако, я писал об оптимизации латентных кодов! Об оптимизации SVD фильтров при помощи Jax, оптимизацию паттернов синего шума и о поиске латентных кодов для обучения словаря. В этом случае, содержимое текстур, это просто набор значений оптимизированных в ходе обучения, например, градиентным спуском или обратным распространением ошибки. Сам процесс не сильно оптимизирован и занимает пару минут (но я уверен, что это может быть намного быстрее).

Без лишних рассуждений, вот численное сравнение качества сжатия количество каналов/PSNR:

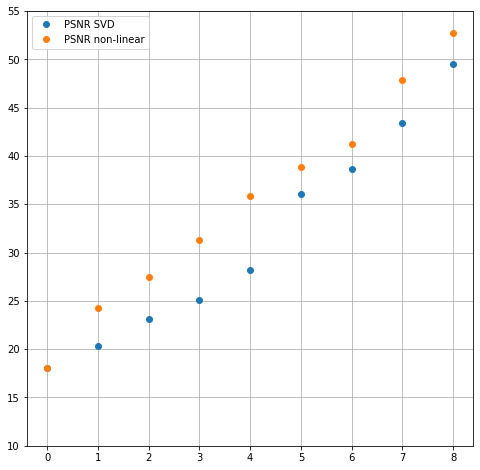
Когда я впервые увидел значения и поведение для очень маленького числа каналов я был впечатлен. Количественное улучшение значительно — более 1 дБ. В случае 4-х каналов сжатие из бесполезного (PSNR ниже 30 дБ), стало достаточно хорошим — более 36 дБ.

Вот визуальное сравнение:

В этом случае вам даже не нужна анимация или возможность переключать изображения туда и обратно. Разница очевидна, как на карте нормалей, так и на карте высот (в центре). Это сравнимо (почти такой же PSNR) с линейным сжатием в 5 каналов.

Это мощь нелинейности — выражать аппроксимацию соотношений между каналами карты нормалей x^2 + y^2 + z^2 = 1, которое невозможно выразить через единственное линейное уравнение.

Как выглядят эти латентные коды? На удивление похожи на данные PCA и обосновано не коррелирующие:

Эффективная реализация

Прежде чем мы пойдём дальше, разберемся, насколько быстрый/медленный данный подход?

Я не измерял производительность, но наиболее прямолинейная реализация это вычисление 64 значений для каждого пикселя, сохранение их на регистрах или LDS через последовательность из 64x4 MAD операций, а затем вычисление 64x9 MAD операций для финальных значений. Всего 832 операции умножения со сложением.

For intermediate channel (64):
  For input channel (1-5):
    Intermediate += Input * weight
    Intermediate = max(0, Intermediate)
For output channel (9):
  For intermediate channel (64):
    Output += Intermediate * weight

Это выглядит дорого, но можно применять всевозможные трюки для оптимизации нейросетей. Я уверен, что можно использовать “тензорные ядра” на железе от Nvidia и агрессивную квантизацию, не только числа типа half float, но так же и 8- и 4-битные типы для большей пропускной способности и векторизации.

Можно производить декомпрессию в некоторое промежуточное хранилище или кеш как с виртуальными текстурами, но я не уверен насколько перспективен этот путь. Последние пять лет обсуждается идея тексельных шейдеров и они могут быть решением данной проблемы, но я далёк от архитектуры GPU последние 4 года и не имею мнения по этому поводу.

Будет ли это работать с билинейной интерполяцией?

Я задался вопросом будут ли закодированные данные портиться при линейной интерполяции (или любой другой линейной комбинации)?

Я провел наиболее простой тест: сделал увеличение разрешения закодированных данных в 4 раза с билинейной фильтрацией, раскодировал их, уменьшил разрешение до исходного и сравнил с декодированными данными. Полученные изображения выглядели достаточно близко, но это всего лишь эмпирический эксперимент на всего одном примере. Я практически уверен, что это будет работать и с другими материалами. Причиной такого поведения я вижу то, что маленькая нейросеть имеет значительно меньше параметров, чем имеется обучающих примеров. Поэтому нет большого пространства для переобучения.

Чтобы объяснить эту интуицию, тут снова приведен пример рассмотренный выше, где меньшее количество параметров и недообученность (слева) даёт хороший результат, в то время как в случае переобучения (справа) поведение будет хуже.

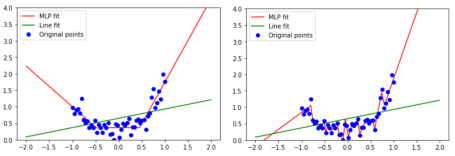
А что если посмотреть на соседей/большую окрестность?

Если посмотреть на текстуры материала, можно прийти к идее, что корреляция между каналами менее очевидна, чем другой вид корреляции — пространственная.

Я имею в виду, что некоторые особенности зависят не только от содержания одного пикселя, но в большей степени от расположения и того, что он представляет.

Например, карта нормалей представляет производные/градиент карты высот и полости или затемнения на карте AO окружены склонами карты высот.

Мы можем использовать либо вычисленные значения, например градиенты, либо просто сверточную нейронную сеть и дать нейросети обучиться на этих не-линейностях, но это может быть слишком медленным.

У меня была другая идея, которая сильно проще/дешевле и кажется, что работает достаточно хорошо — почему бы просто не посмотреть на размытую версию окрестности текселя? В пределе это будет практически бесплатная аппроксимация — если мы посмотрим на следующий уже сгенерированный MIP-уровень.

Поэтому в качестве входа нейросети я добавил чтение ещё двух MIP-уровней (полученных уменьшением разрешения в 4 раза и увеличением их обратно).

Это улучшило результаты довольно значительно в моём любимом (сильное сжатие, хорошие результаты PSNR) режиме на 2-5 выходных канала:

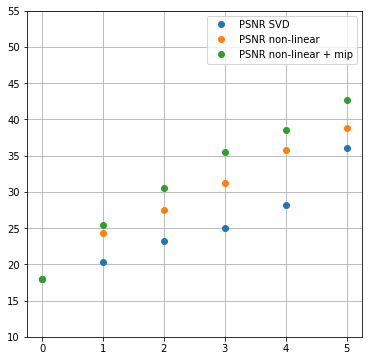
Может получилось не так уж впечатляюще, но с добавлением этих двух каналов улучшающими PSNR мы сохраняем 3 канала и реконструируем 9 c 35.5 дБ место 25 дБ. Это значительное улучшение!

Почему бы не пойти дальше к полному глобальному кодированию и координатным сетям?

Успех недавно появившихся техник в нейронном рендеринге и компьютерном зрении, где входные данные — это просто пространственные координаты (как в блестящем NeRF), вызывает вопрос — почему бы не использовать тот же подход для сжатия материалов/текстур? Насколько я понимаю, полностью обученный NeRF использует больше данных, чем дано на вход (расширение вместо сжатия!), но даже если мы обратимся к гибридному подходу (какой-то латентный код + смесь координат и обычного входа нейросети), для использования на GPU нам не нужно представление “глобальной поддержки” (где каждый кусочек информации описывает поведение/декодированные данные во всех точках).

Если вам нужен доступ к информации всей текстуры для кодирования единственного пикселя, то ваши данные не влезут в кеш… И в этом нет никакого смысла. Об это можно думать примерно в следующем ключе — если вы рисуете открытый мир, то хотелось бы вам чтобы для отрисовки одного маленького объекта вам требовалась вся информация о другом объекте находящемся в 3 милях или 5 км?

Поддержка локальности гораздо эффективнее (так как требует чтения данных полностью попадающих в кеш) и даже техники типа JPEG, которые использую глобальный контекст, делаю это внутри небольшого локального тайла.

Нейронная декомпрессия линейных SVD-данных

Эта идея возникла у меня во время экспериментов с пространственными отношениями. Может ли “нейронный” декомпрессор научиться осмысленному нелинейному декодированию линейно закодированных данных? Мы могли бы использовать обученный декодер на быстро линейно закодированных данных.

Такой подход имеет два значимых преимущества:

1. Компрессия/кодирование будет значительно быстрее.

2. В зависимости от скорости/производительности (или доступности памяти в случае кеширования) платформы, можно выбрать либо быструю линейную декомпрессию или нейросетевую.

3. Художники могут работать с линейными SVD-данными и имеют гарантию, что финальный результат будет иметь более высокое качество на высокопроизводительных платформах.

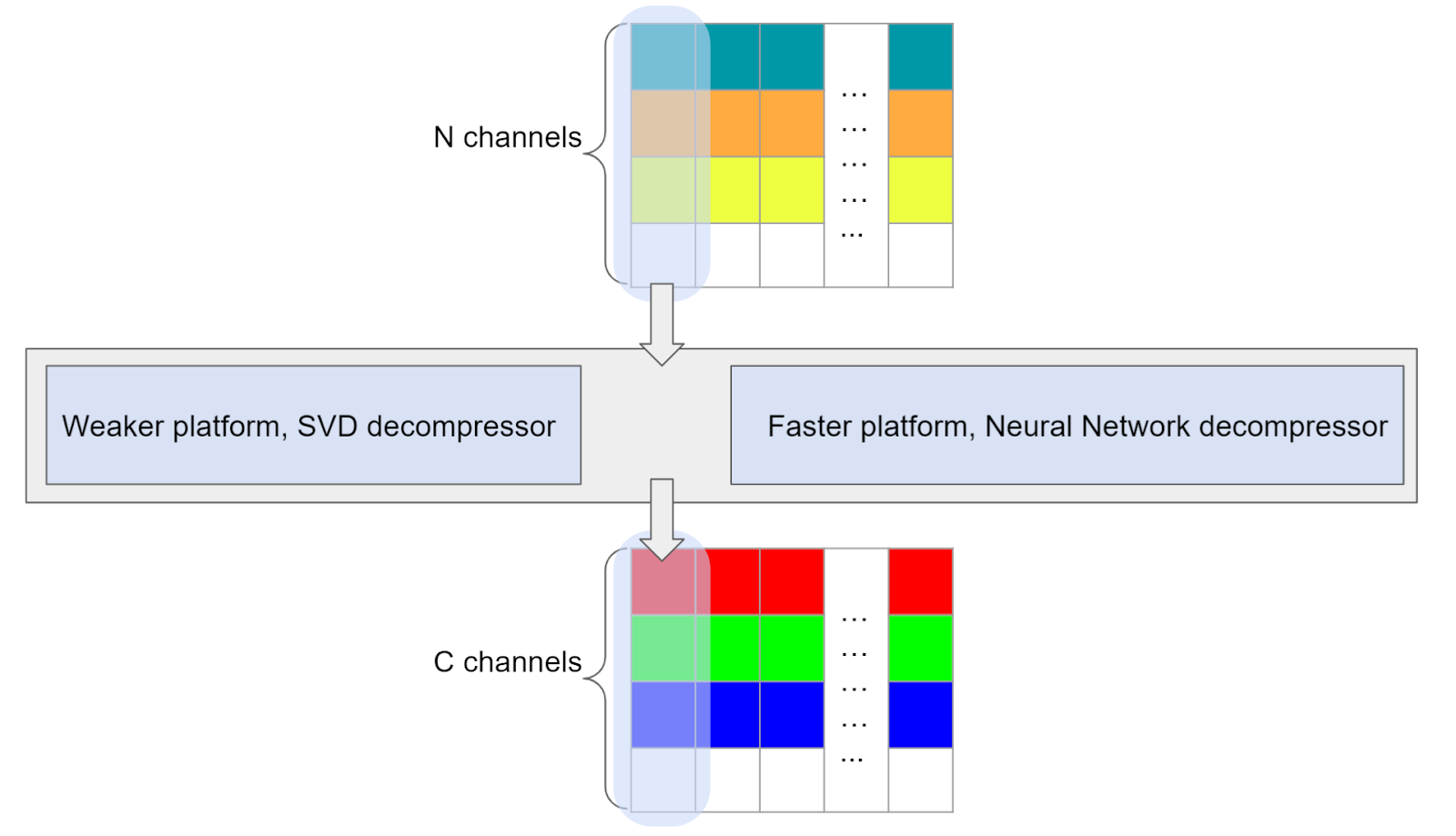
В такой постановке, мы берем латентные коды посчитанные через SVD и оптимизируем только сеть. Сеть имеет доступ к латентным SVD-кодам и двум следующим мип уровням.

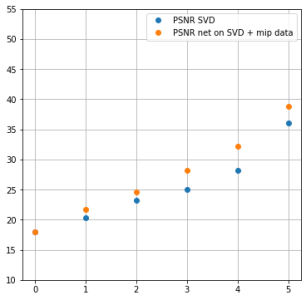
Результаты не такие впечатляющие как раньше, но всё равно на 4 дБ лучше на тех же самых данных, что интересно и может быть полезным результатом.

Хранение G-buffer’а

В качестве заключение отметим, что в некоторых случаях маленькие нейронные сети могут быть использования для декодирования данных хранящихся в G-buffer’е в контексте отложенного освещения. Если несколько различных материалов могут храниться в одном и том же представлении, то декодирование может быть выполнено непосредственно перед вычислением освещения.

Это не настолько безумная идея, как может показаться. Хотя выигрыш от компрессии может оказаться более скромным, я вижу другое достоинство: многие игровые движки, использующие отложенное освещение, содержат рукописный спагетти код, который пакует материалы различных типов с разными наборами свойств и столь же сложную декодирующую функцию.

Когда я работал над GoW, я тратил недели на “оптимальные” схемы упаковки, которые были бы компромиссом между потребностями различных художников и различными типами материалов (анизотропный спекуляр, подповерхностное рассеивание, самоотраженный спекуляр, диффуз с различными профилями…)

… а так же были различные типы кодирующих/декодирующих функций, такие как линеаризация шероховатости и последующая её конвертация в другое представление для вычисления текущей ДФОС. Много работы, которая была интересной (славный вызов!) в своё время, но в то же время трудоёмкая и иногда душераздирающая (когда вам приходится выбирать между тем, что игра будет использовать большее количество памяти и потеряет 10% производительности, и тем чтобы сказать художникам, что фича, которую вы написали для них и которую они любят, не будет больше поддерживаться).

Это может быть удивительной экономией времени и разгрузкой программистов, если положиться на автоматическое декодирование вместо таких несовершенных эвристик.

Заключение

В этом посте я вернулся к некоторым идеям совместного сжатия набора текстур материала, полагающихся на корреляцию между текстурами.

На этот раз мы исходили из предположения о существовании нелинейных корреляций в данных и использовали крошечные нейросети чтобы обучить их на этих соотношениях для эффективного представления и уменьшения размерности.

Мои эксперименты далеки от чего-то завершенного или применимого. Это в большей степени обзор идеи, набросок, требующий разработки многих деталей и заполнения многих пробелов. Но эта идея определенно работает! И даёт реальное, измеримое улучшение (на ограниченном наборе примеров, который я попробовал). Попытаюсь ли я использовать это в продакшене? Я не знаю. Возможно я поиграюсь ещё со сжатием наборов текстур материала если у меня будет жуткая нужда в уменьшении размерности размера материала, но с другой стороны я бы потратил время на развитие идеи компрессии G-buffer’а (хотя понимаю, что это может быть не так просто на практике).

Если можно сделать из всего этого какой-то вывод, помимо развлечений с компрессией наборов текстур, я надеюсь, что это будет некоторая демистификация использования нейронных сетей для задач ориентированных на данные:

• Это всё исследование нелинейных зависимостей во множестве сложных данных с большими размерностями.

• Несмотря на ограничения (ReLU может представлять только кусочно линейную аппроксимацию функции) этот подход действительно может быть использован на практике.

• Вам не нужно запускать гигантскую нейросеть с миллионами параметров чтобы получить какой-то выигрыш.

• Маленькие сети могут быть полезными и быстрыми (832 умножения со сложением на данных с ограниченной точностью вполне применимы на практике).

Дополнение: Я добавил некоторые примеры кода для этого поста на GitHub/Colab. Там всё запутано и не документировано, так что используйте на свой страх и риск (предпочтительно с GPU Colab).