Натолкнулся в Интернете на задачу, которая называется "Теорема о четырех красках".
Вот ее страница в Википедии. Если не знаете эту задачу, то прочтите - интересная история.
Сама задача звучит так: сколько минимум нужно красок, чтобы раскрасить государства на карте, и при этом чтобы все граничащие территории имели разный цвет?
Многократные попытки решить эту задачу в течение последних ста лет интригуют, а итоговое ее решение исключительно благодаря компьютерам и некоему "специальному программному обеспечению" звучит как-то не очень убедительно. Поэтому попробуем разобраться самостоятельно.
Приступим.
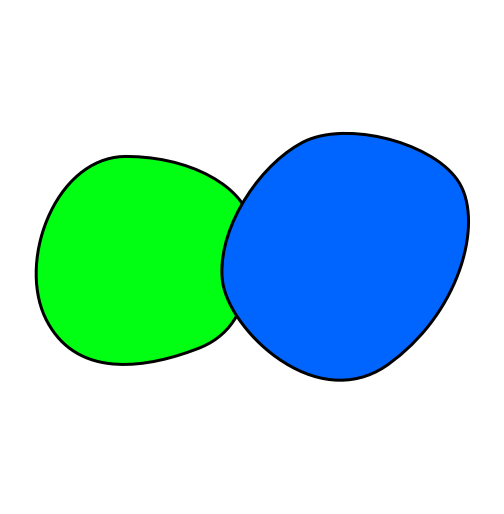

Как видим, одновременно два граничащих государства (рис.1) требуют два, а три граничащих государства (рис.2) - три разных цвета.

В случае с одновременно четырьмя граничащими государствами (рис.3) потребуется четыре цвета.
И на этом рост количества цветов заканчивается, а пятый цвет уже не понадобится. Почему так?
Потому что когда одновременно граничат четыре государства, то одно из них обязательно оказывается полностью окружено тремя другими и больше ни с чем уже граничить не может. Его цвет высвобождается для дальнейшего использования, а продолжение окрашивания возвращается к предыдущему шагу с тремя одновременно граничащими государствами (рис.4).

Разберем этот момент подробнее и покажем, почему в случае с четырьмя одновременно граничащими государствами одно из них всегда оказывается изолированным от всех остальных, что высвобождает его цвет для последующего шага окрашивания.


Для большей наглядности заменим государства точками, а их пограничные контакты обозначим соединяющими точки линиями (рис.5). Посмотрим, почему справедливо утверждение, что при одновременном соединении всех четырех точек одна из них обязательно окажется внутри трех других (рис.6).

Пусть исходно (рис.7) у нас есть три соединенных точки (точки 1, 2 и 3). Будем присоединять к ним четвертую точку (точку 4).


Соединив точку 4 с точками 1 и 2, нам остается соединить ее с точкой 3. Сделать это можно либо с одной стороны (a), либо с другой стороны (b). А такое соединение делает внутренней одну из двух точек (точку 1 на рис.8 или точку 2 на рис.9). Поэтому одновременное соединение четырех точек обязательно приводит к изоляции как минимум одной из них.
В контексте нашей задачи это означает, что при одновременном контакте четырех граничащих государств требуется четыре цвета, но при этом один из цветов становится внутренним и высвобождается для следующего шага раскрашивания. Поэтому пятый цвет не потребуется.
Более того, из изоляции одной из точек уже при четырех цветах также следует, что невозможно существование одновременно пяти граничащих государств.
Как и авторам решения этой головоломки из вышеуказанной статьи в Википедии, нам для решения этой задачи также потребовалась современная компьютерная техника и специальное программное обеспечение: мне - для того, чтобы написать этот текст, а вам - чтобы прочитать его.
Комментарии (27)

emaxx
26.06.2022 17:45+8Не только четыре одновременно граничащих государства требуют 4 цвета. Любое государство, окружённое нечётным числом других, приведёт к использованию 4 цветов (потому что при попытке раскрасить в 3 цвета получилось бы 232323...32 - нестыковка начала и конца).
Кроме того, вы не доказали исходную задачу, а лишь задачу "одно государство, окружённое другими". Потому что у вас нет доказательства того, что при описанной вами стратегии не возникнет противоречия между раскрасками дальних соседей.

Radisto
26.06.2022 20:12+7А если натянуть карту на тороидальную поверхность, то четырех может и не хватить. Там может понадобиться 7

Machirodont
26.06.2022 17:47+20Чудесно! Автору предлагаю также заняться поиском простого доказательства теоремы Ферма и построением вечного двигателя. А то ученые-моченые чего-то там мудрят все время.

valergrad
27.06.2022 00:52+3Надеюсь автор сам понимает насколько стебно его "доказательство" и просто решил всех развлечь. Хотя возраст автора в профиле является косвенным свидетельством что это не так. В возрасте за 50 больше шансов наткнуться на упертого в своем невежестве фрика, чем на шутника.

GlukKazan
26.06.2022 18:07Есть нюанс. На самом деле, задача заключается в том, чтобы доказать, что четырёх (или пяти) красок достаточно для раскраски любой (контурной) карты. При этом, нет требования, чтобы каждым цветом закрашивалась только одна область. Есть только требование того, чтобы области имеющие общую границу закрашивались разными цветами. Здесь есть небольшая вина Мартина Гарднера, как популяризатора задачи. В своём рассказе "Остров пяти красок", он не утрудил себя правильной формулировкой задачи.

aamonster
26.06.2022 19:34+1Нормальная там формулировка. Во всяком случае, в том переводе, по которому только что проверял.

GlukKazan
26.06.2022 20:01Согласен, я сам немного не точно сформулировал. Формулировка проблемы нормальная (прямо в третьем абзаце рассказа), но дальше он уже раскрашивает не любую, а вполне конкретную карту стран, расположенных на острове, причём, поскольку это именно страны, каждая из них представляет собой регион, состоящий из одного куска, что немного вводит читателя в заблуждение, относительно самой задачи (меня во всяком случае ввело, когда я это читал в первый раз).

Pochemuk
26.06.2022 20:58Автор рассмотрел один из частных случаев, когда добавляемая область касается трех других. Но она может касаться и двух и только одной уже существующих. В этом случае исключение цвета происходить не будет.

andres_kovalev
27.06.2022 01:46В этом случае ее можно раскрасить цветом той страны, с которой она не граничит - т.е. новый цвет не нужен.

Pochemuk
27.06.2022 22:22Если добавляемая область граничит с двумя раскрашенными, то ее можно раскрасить в один из двух цветов. Допустимо ли выбрать любой из этих цветов, чтобы в перспективе не возникла ситуация, требующего применения пятого цвета?
В комментарии показано, что это не так.
По сути имеем не одну проблему, а две:
1. Доказать, что для раскраски любой карты четырех цветов достаточно.
2. Разработать алгоритм последовательной раскраски областей — определить критерии выбора следующей раскрашиваемой области и ее цвета, не приводящие в сколь угодно дальней перспективе к противоречию п.1.
Medeyko
27.06.2022 23:07+2Дело даже хуже: невозможно разработать алгоритм последовательной раскраски областей, картину нужно рассматривать полностью, в совокупности.

Возвращаясь к тому моему примеру, на который Вы сослались.
Предположим, что на 12-м шаге областью стало не кольцо, а тоже кусочек.
Тогда с построением всё нормально.
Теперь перекрасим так, как я предложил, чтобы не было проблем на 12-м шаге с закраской кольца.
На 12-м кольцевом шаге проблем не будет, да.
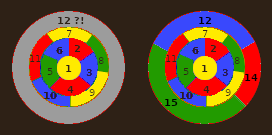
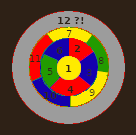
Но зато если на 12-м шаге областью станет не кольцо, а кусочек, на 15-м шаге опять возникнет проблема.Таким образом, последовательно раскрашивать, не зная, что будет дальше, невозможно. Нужна вся картина сразу.

Medeyko
28.06.2022 00:09Пропустил 13 (хотя вроде как я не суеверный!) - после 12 у меня сразу идёт 14, ну да надеюсь, всё равно понятно.
Раз уж пишу комментарий, то добавлю, что в последнем варианте нам не поможет и другой выбор цвета на 12-м ходу: если выбрать вместо синего красный, то на 14-м (который должен был быть обозначен как 13-й) придётся выбрать синий, и на 15-м всё равно возникает проблема.
(Ну и за техническое качество иллюстраций снова прошу извинить, надеюсь, что ни у кого глаза не вытекли.)

yurixi
28.06.2022 05:59Невозможность построения алгоритма последовательной закраски можно объяснить рассуждением. Последовательная закраска для определённого момента это разделение карты на две области, «до» и «после». Область «после» не зависит от области «до» и можно менять конфигурацию. Но возможность раскрасить в четыре цвета исходит из того, что известна вся карта, то есть, при изменении конфигурации в одной части в общем случае может понадобиться по-другому распределять цвета в другой части. Чтобы алгоритм последовательной раскраски существовал, нужно чтобы раскрашенная область «до» подходила к любой области «после» — к каждому варианту, а это не так.
Я бы вообще предложил бы красить не в цвета, а в «возможности». То есть, хранить для каждой области дозволительные варианты раскраски. И тогда связи между областями будут «в случае такой раскраски соседних областей остаются такие варианты для этой». Но под «раскраской соседних» здесь понимается комбинация соседних «цветов», поэтому различающихся вариантов раскраски областей может быть больше четырёх, один цвет области при разных ограничениях это разные «цвета». Могут быть такие комбинации соседних цветов, что варианта для области не останется. Но этот вариант исключается из рассмотрения, а теория о раскраске говорит, что исключать такое можно спокойно, меньше одного варианта для всей карты не останется.

yurixi
27.06.2022 06:16+3Я думал написать про теорию о четырёх красках, но для этого нужно соблюдать полнейшую точность определений и иметь мощную самопроверку, а не то получится такое же недоразумение. Хуже было бы, если бы это выглядело продуманным, а являлось бы тем же самым.
Но — хороший повод выложить свой написанный фрагмент.
Теорема о четырёх красках.
Существует довольно простое предположение, что после разделения плоскости на области, такого чтобы в углах они встречались не больше чем по трое, эти области можно раскрасить так, чтобы соседи не были раскрашены одинаково. И что хватит четырёх красок. Так как плоскость в топологии аналогична поверхности шара, доказать что не хватит трёх красок легко: спроецировать на сферу тетраэдр — и вот вам четыре участка, каждый соседствует один с другим, четыре цвета обязательны. Но хватит ли четыре цвета для всех видов разделения? Ведь тогда любое разделение можно спроецировать обратно на тетраэдр.
Предположим, что у меня есть задача доказать теорему. Я бы начал с описания нарушающего случая. У нас будет область, которая имеет как минимум четыре соседа, таких, которые обязательно различаются между собой. На графике, отражающем линии, проводящие эту недопустимость сходства лежат так, что у них обязательно есть пересечение. Это можно отметить для исследования. Если бы был способ передавать соседство на расстояния, то либо его нельзя представить линией передачи, либо задача сводится к самой себе: доказать что невозможно две таких передачи пересечь.
Рассмотрим дальнюю передачу соседства, в некотором виде оно возможно. Это можно сделать через обязательное совпадение первой областей и соседней ко второй, тут без такого соседа ко второй не обойтись. В свою очередь дальней передачи цвета можно достичь, если сделать так, чтобы между этими областями были расставлены все посредники, количество которых на единицу меньше количества используемых красок. В данном случае, получается, три, хотя к этому количеству уже могут быть вопросы, ведь количество красок у нас четыре условно. Но тут появляется кое-что ещё: принципиальная необходимость того, что эти трое цветов соединились в опоясывающий контур, иначе два цвета будут разделены между собой третьим и появляется возможность сменить цвет одной области на повторяющий. А не допустить смены цвета можно только если как-то другим способом передать соседство. А что это за другой способ? Разве такой есть?
Итак, опосредованно соседство не передать, либо способ неизвестен, а непосредственное соседство сводит задачу к ней же самой. И здесь ситуация, в которой, как говорится, предполагаемое либо не получится, либо одно из двух.
Не смотря на незаконченность, это может выглядеть как перспективный черновик на доказательство. Развивать можно, уточняя определения и схемы проверки. Но уже здесь кое что упущено. По логике, само существование десятого запрета в группе пяти областей, обязательно создающего пересечение, вовсе не обязательно. Достаточно того, что расставленные цвета действительно различаются, а запрет может быть симулирован через запрет менять цвета. Запрет одинакового соседства и запрет смены цвета как невозможность перерасстановки при соблюдения первого запрета — могут быть разными запретами. В случае если доказываемая теорема не верна.
Мы не избавились от необходимости в полноте и точности закончить доказательство, ничего не доказано. Похоже, теперь — нужно разобраться в том, почему поменять цвета в случае завершённой расстановки будет невозможно. Только, изначально доказываемая теорема предполагает о том что это возможно. Так что, очень сложно рассмотреть этот запрет — рассмотреть то, что предположительно не существует. Теорема оказалось действительно сложна в доказательстве, как за неё не возьмись — она выглядит как «а почему бы и нет».
***
Даже это — то что я написал — не сообщает о доказательстве ничего. Некоторые утверждения при дальнейшем разборе наверняка окажутся не точны, не верны. Но это лучше чем: «смотрите, схема в которой хватает четырёх цветов существует, я математег.»
Не знаю, возможно ли простое доказательство, но оно — не на столько простое.
ermouth
27.06.2022 18:39+1Так как плоскость в топологии аналогична поверхности шара
Это не так. Чтобы сфера стала гомеоморфна плоскости, нужно из сферы выколоть одну точку. После этого пример с тетраэдром перестаёт быть очевидной иллюстрацией, вообще говоря.

yurixi
28.06.2022 09:14Я думал вы шутите, и пошутил в ответ. Но для тех кто воспринял вас всерьёз тут нужно пояснить: раскраска областей и вопрос гомеоморфности сферы и плоскости никак не связаны, так как при раскраске рассматривается не столько плоскость, сколько плоский граф. Это многие вопросы сразу убирает. Но даже если действительно рассмотреть вопрос связи, сами подумайте: исключаемая точка может попасть только в область, ребро, узел — в любом случае вообще ни на что не влияет, правила заполнения не зависят от одной точки, можно хоть миллион точек исключить.
Вообще, даже интересно заметить, что есть две крайности: автор топика, который говорит «всё просто, верьте мне», и верит сам. И вы, «всё сложно, верьте мне». А может в это не стоит верить? Вы запутали не только лишь себя.
ermouth
28.06.2022 09:44+1Плоскость в топологии всё же не аналогична сфере, поэтому я обоснованно усомнился в ваших дальнейших рассуждениях.
И вы, «всё сложно, верьте мне». А может в это не стоит верить?
Я такого не говорил. Я сказал, что всё не так очевидно.
и вопрос гомеоморфности сферы и плоскости никак не связаны,
Это многие вопросы сразу убирает.
Не уверен, потому что если точку не выкалывать, вся дальнейшая модель кажется забывает о существовании бесконечной грани. Возможно, это не так, с учётом вашего замечания о независимости заполнения от выколотых точек.
Вашему черновику доказательства я пока не верю, потому что вы начали с ложного утверждения – так не принято даже в целях упрощения – но точно посмотрю внимательней, интуиции мне здесь не хватает.
Спасибо за аргументированное возражение.

yurixi
28.06.2022 10:49В «черновик доказательства», можете и не вникать, я там вижу несколько мутных моментов. «Задача сводится к самой себе» — это очень смешная с формулировка с математической точки зрения. Впрочем, если особенная область заставляла бы цвета соседних областей быть между собой различными, она бы и себя заставила быть новым цветом.

ermouth
28.06.2022 17:03Ок, для укладки планарного графа сфера и плоскость – действительно одно и то же, это элементарно доказывается, в одно соображение, я просто затупил. Считайте мой коммент просто уточнением вашей формулировки.

dmitryvolochaev
27.06.2022 09:03+3Коварство задач на доказательство в том, что правильность доказательства тоже еще доказать надо

s_f1
27.06.2022 10:23Кому некогда ходить по ссылкам – вот подробности:
Теорему доказали, прогнав через компьютер полторы тысячи конфигураций карт, с претензией на существование контрпримера. Но некоторых такое доказательство не убедило, как из-за привлечения компьютера, так и из-за метода подбора карт-кандидатов. Поэтому теорему периодически доказывают (вернее – проверяют) снова и снова. Правда, меняется только мощность компьютеров и эффективность алгоритмов, но суть доказательства остаётся похожей. Кое-кто решил зайти через снарки, но пока, вроде, строгого доказательства нет.

Medeyko
27.06.2022 12:40+6Когда читал это "конструктивное доказательство", ожидал, что в конце будет написано что-то в духе "Но конечно же, всё не так просто. Рассмотрим, что не так с этим как бы доказательством..." Увы, не дождался.
Проблема в том, что в этой статье не показан индуктивный переход, не доказано, что проблем не возникнет и дальше, при усложнении картины.
В качестве примера покажу картинку, которая строилась по неявно предполагаемому в статье конструктивному алгоритму, и в которой на 12-м шаге невозможно выбрать цвет:
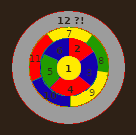
(Прошу простить за низкое качество иллюстрации) Разумеется, эту картинку можно перекрасить так, чтобы проблемы не было: если на 4-м ходу вместо красного закрасить зелёным, на 5-м - красным, на 11-м - зелёным, то на 12-м ходу можно закрасить красным.
Но в статье не предлагается выбор цветов и не доказывается, что он корректный.
И, вообще говоря, Стивен Барр игру такую придумал - "четыре краски" для двух игроков. Первый игрок рисует пустую область, второй её закрашивает одним из цветов и добавляет свою пустую область. Первый игрок также закрашивает её одним из четырёх цветов и в свою очередь рисует пустую область. Выигрывает тот, кто нарисовал пустую область, граничащую со всеми четыремя цветами.



Aspos
Ну то была конкретная карта графвтв Англии.
Не любая карта, конечно же.
Aspos
Ок, дошло, спасибо.
Maxik12
А что мешает сделать так?