Меня зовут Саша, я разработчик библиотеки ETNA в Тинькофф. Расскажу про методы EDA в библиотеке ETNA, а также о том, что можно увидеть с их помощью в данных и как использовать для улучшения модели прогнозирования.

Условия задачи

Попробуем найти что-то интересное во временных рядах из соревнования Web Traffic Time Series Forecasting. Организаторы предлагают участникам спрогнозировать количество посетителей страниц Википедии, а качество прогнозов оценить по SMAPE. Поэтому в статье будем ориентироваться на эту метрику.

В предыдущих статьях наша команда рассказывала, как прогнозировать временные ряды и как использовать для этого дополнительные данные. Если бейзлайн уже построен, метрики перестали улучшаться — самое время вернуться на шаг назад и приступить к EDA.

Выбросы, пропуски и прочие неприятности

Пропуски. В условиях соревнования указано, что в данных есть пропуски. Организаторы подсказывают, что они могут возникать из-за отсутствия данных или просто из-за того, что трафик в этот день был нулевой.

Попробуем визуализировать разные варианты заполнения пропусков. Заполнение нулями выглядит не очень правдоподобно:

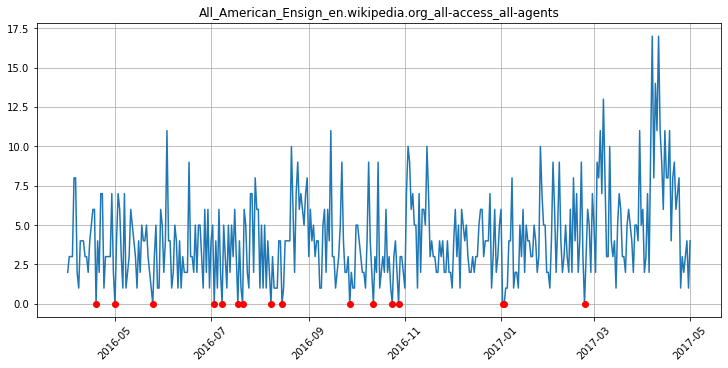
Последнее известное значение выглядит лучше, но может плохо работать, если пропуском является целый интервал:

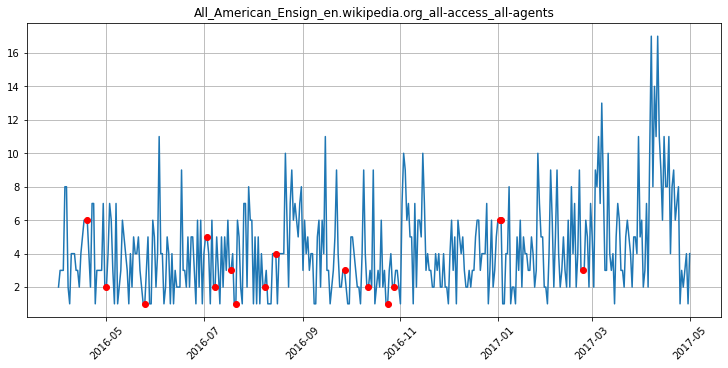
Скользящее среднее последних трех дней выглядит как идеальный вариант:

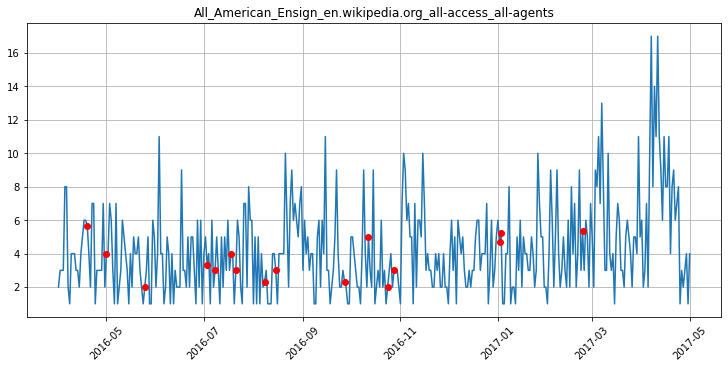
Выбросы. Заполнили пропуски — стало понятнее. Остались выбросы и аномалии. Выбросами назовем необъяснимые пики или сдвиги уровня ряда в случайные моменты времени. Чаще всего это следствия сбоев или ошибок при выгрузке данных, и они не отражают поведения ряда.

Для обработки выбросов есть методологии на любой вкус и цвет. Например, можно добавить специальный признак-индикатор, заменить выбросы, как мы это делали с пропусками, или просто выкинуть из датасета. Попробуем второй путь.

В нашей библиотеке есть целый набор методов для детектирования выбросов. К сожалению, все методы страдают общим «недугом» — для них нужно подбирать гиперпараметры:

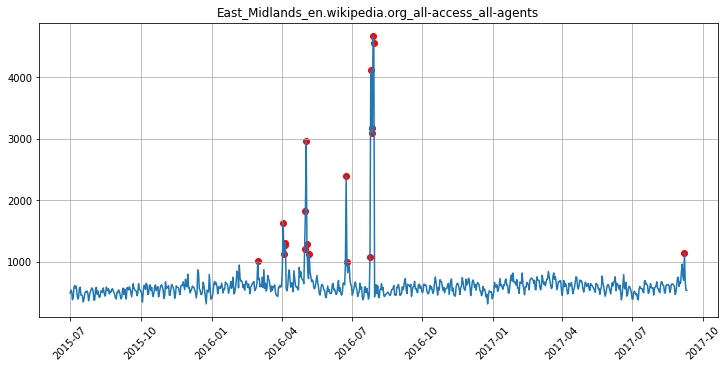
Параметры можно подбирать и в интерактивном режиме, пример — в ноутбуке по ссылке выше.

Попробуем спрогнозировать наш ряд на шесть недель вперед, оставив выбросы на месте, а затем «исправив» их, как договорились выше:

Сравним качество прогноза по метрике SMAPE с выбросами и без: 

Обработка выбросов улучшила нашу метрику примерно на 15%! Выглядит как убедительный довод в пользу того, что обработка выбросов — это определенно важная часть пайплайна прогнозирования.

Аномалии. Появление выбросов в ряде невозможно предсказать из-за их случайной природы, но в рядах есть и другие аномальные участки. Некоторые из них на первый взгляд ничем не отличаются от выбросов — например, пики в праздничные дни. Такое поведение ряда ожидаемо, и можно попробовать научить модель его предсказывать. Разберемся, как это делать, на примере ряда, связанного с сериалом Black Sails.

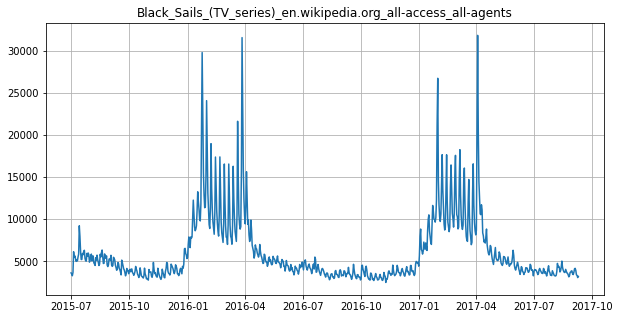
Аномальное поведение в начале года — выход очередного сезона. Нам известно об успехах первого сезона сериала в 2016 году, можем оценить нагрузку на сервера в период выхода новых серий в 2017 году.

Например, популярная модель Prophet умеет из коробки учитывать эффект таких событий, но для этого нужно подобрать параметры событий:

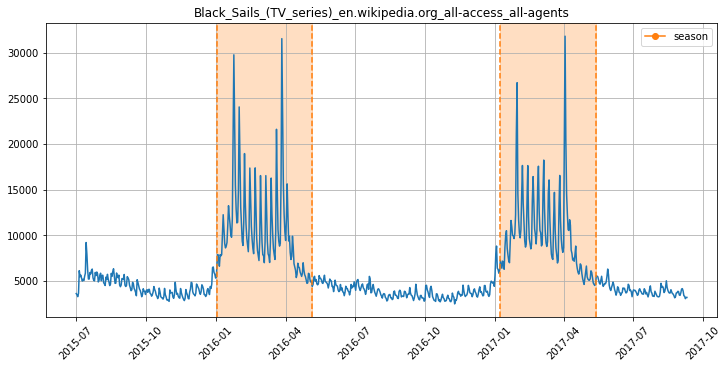
Дата выхода сериала известна, окно зависимости от выхода сезона мы определили, можно прогнозировать 2017 год. Попробуем сделать прогноз тремя способами — с дефолтными параметрами, с включенной годовой сезонностью и с включенной годовой сезонностью и учетом выхода сезона:

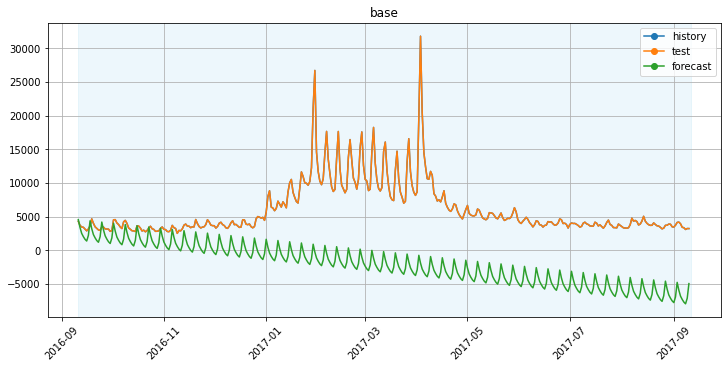
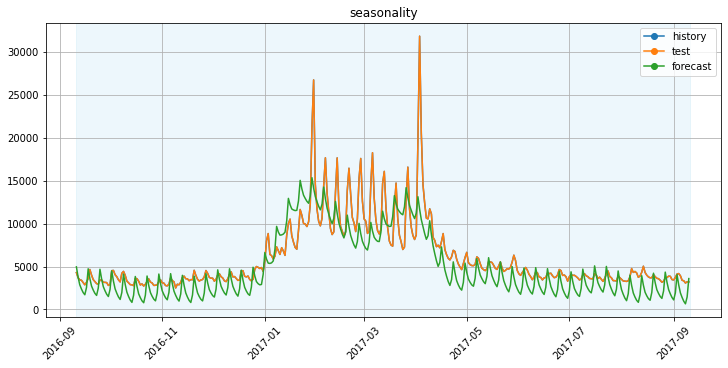
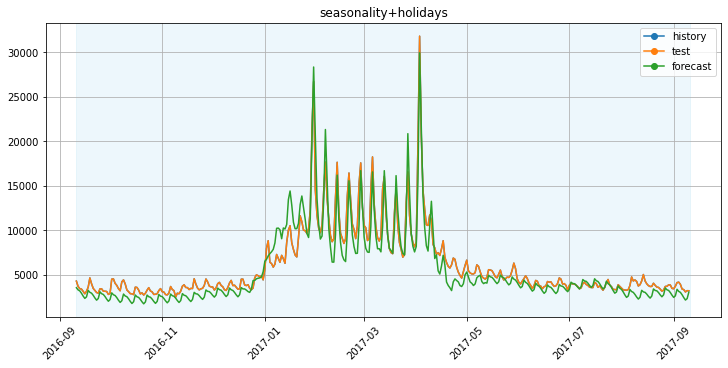
Мы попробовали три конфигурации модели Prophet, сравним метрику SMAPE:

Без учета эффекта выхода нового сезона в модели предсказать ничего особо не получается. Годовая сезонность улучшила картину, но информация о новом сезоне улучшила метрику еще в два раза.

Тренд и сезонность

Более глобальные свойства временных рядов — тренд и сезонность.

Сезонность — периодические колебания значений ряда.

Включение в модель годовой сезонности улучшило качество в предыдущем примере, но есть подозрение, что в данных могут присутствовать и более мелкие сезонности.

Для определения сезонности используем инструменты из нашей библиотеки. Все начинающие специалисты по временным рядам сталкивались с графиком автокорреляции. Его и используем, смотрим на соседние значимые пики, и видим недельную сезонность:

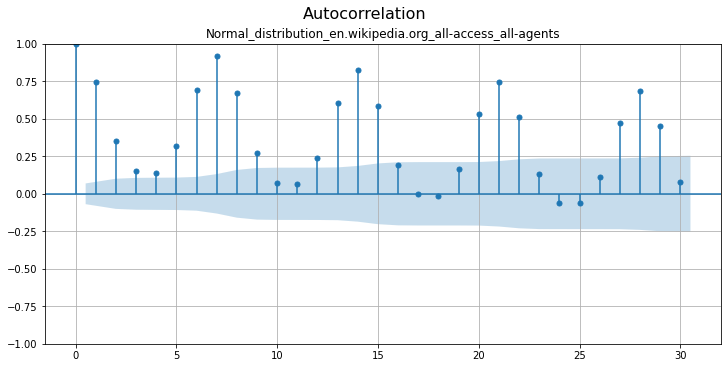
Посмотрим на более экзотичную картину — периодограмму. На ней изображены амплитуды компонент ряда Фурье с периодом в год:

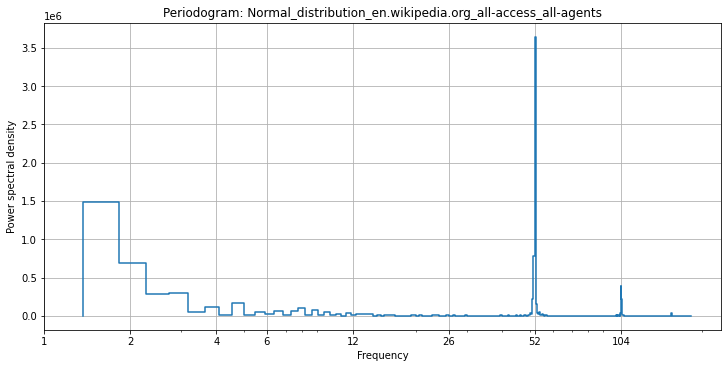
Попробуем другую модель, Catboost, и смоделируем недельную сезонность с помощью метки дня недели, а более длинные сезонности — с помощью признаков Фурье:

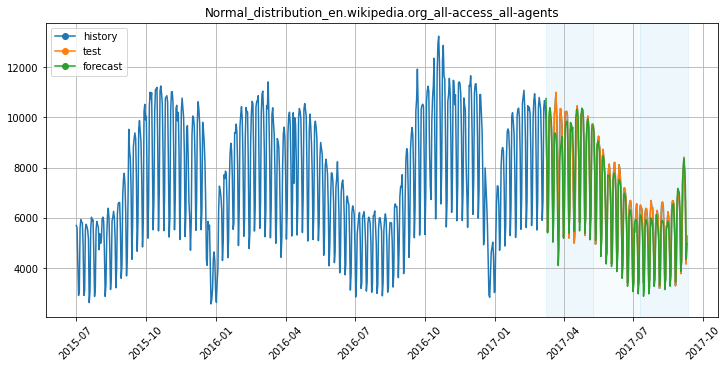
Видим, что модель успешно уловила годовую и недельную сезонность, можем двигаться дальше и переходить к тренду.

Тренд — глобальная тенденция изменения показателей временного ряда.

В нашей библиотеке реализовано несколько методов моделирования тренда, их также можно визуализировать и, конечно, добавить в пайплайн:

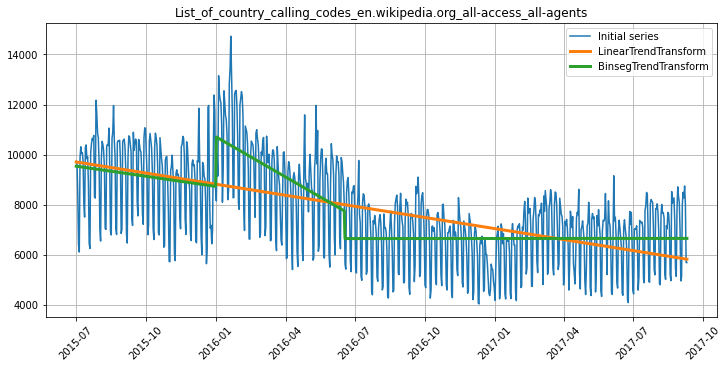
Визуализация подсказывает нам, что тренд у ряда лучше моделировать кусочно-линейной функцией. Давайте проверим, действительно ли это так, на практике. Попробуем спрогнозировать ряд тремя способами: без моделирования тренда, моделируя тренд линейной функцией и моделируя тренд кусочно-линейной функцией:

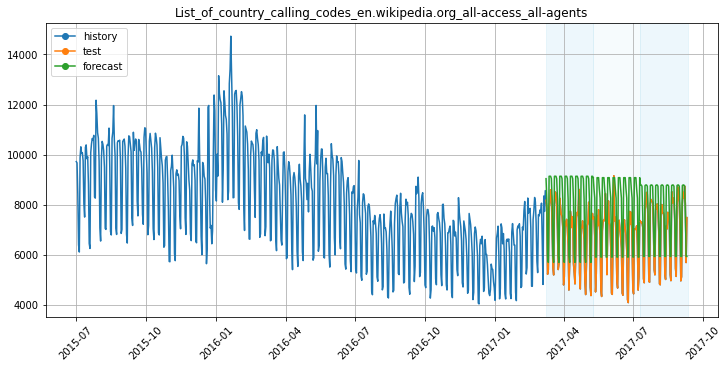
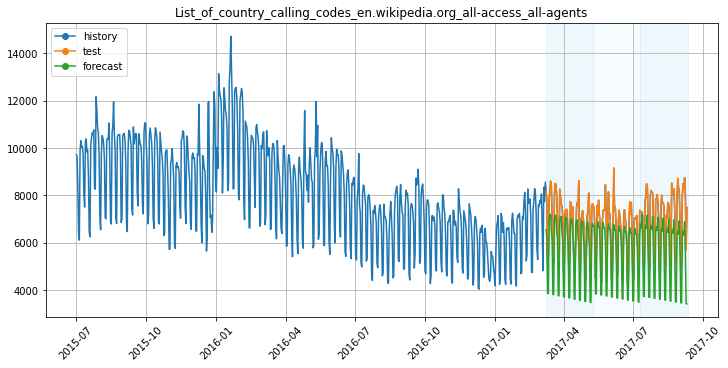
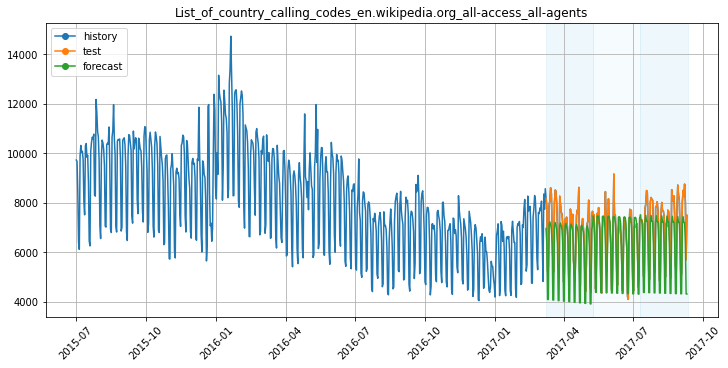
Сравним качество прогноза для рассмотренных методов по метрике SMAPE:

Использование кусочно-линейной функции для моделирования тренда улучшает качество прогноза на 37% относительно пайплайна прогнозирования без моделирования тренда. При этом моделирование тренда линейной функцией даже ухудшает качество.

Анализ качества модели

На протяжении статьи я показал различные особенности в отдельных сегментах, но стоит помнить, что датасет состоит из 145 тысяч рядов. Не будем травмировать наши вычислительные мощности и попробуем спрогнозировать случайные 100.

Представим, что этап борьбы с данными позади, есть пайплайн и нужно оценить, насколько он хорош. Запустим бэктест и визуализируем результаты, как мы уже делали это ранее. Хотя разглядывать картинки для 100 сегментов — так себе идея. Предлагаю посмотреть, как распределена целевая метрика:

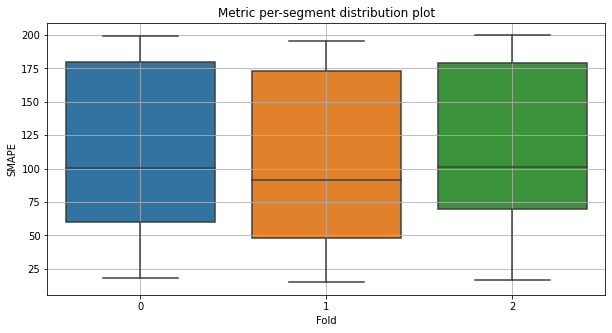
Неплохой разброс. Посмотрим, какие сегменты мы прогнозируем лучше и хуже всего:

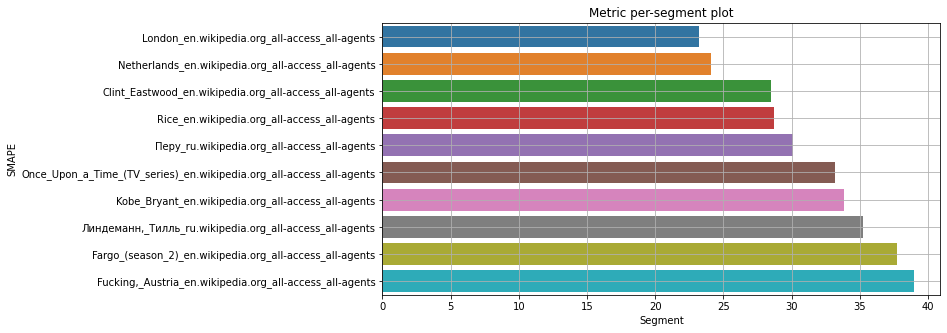
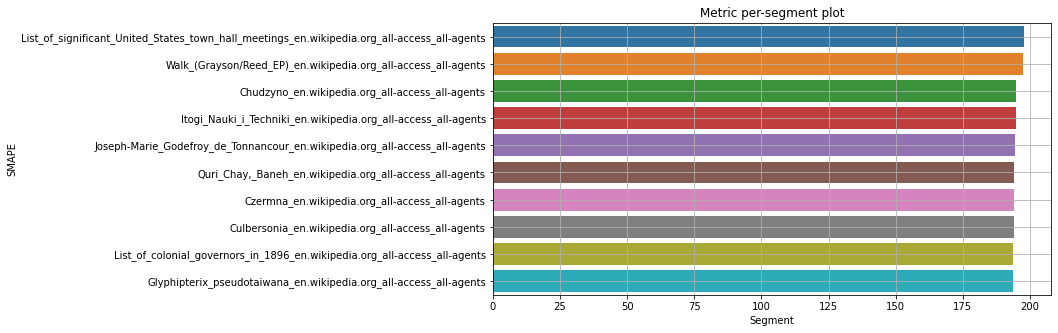
Посмотрим на важность признаков:

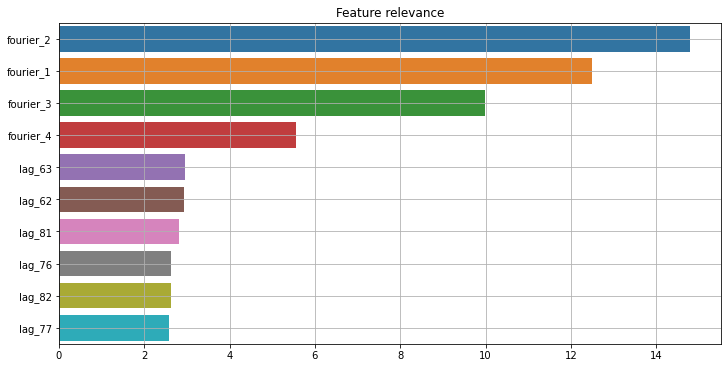
Вместо итогов

В статье мы рассмотрели различные особенности данных, которые могут существенно влиять на качество прогнозирования. В их числе могут выступать аномальное поведение, выбросы, сезонность, тренд и многое другое. Обнаруживать эти особенности нам помогают методы EDA, при этом большую часть интересных находок из этих методов можно легко добавить в пайплайн прогнозирования и задешево улучшить качество нашей модели. Надеюсь, мне удалось убедить вас, что EDA — это полезный шаг при построении пайплайна.

Если статья вам понравилась, не стесняйтесь ставить нам звездочки на GitHub. Для тех, кто хочет самостоятельно покопаться в данных и попробовать все наши методы EDA в деле, прилагаю код для загрузки данных.