Алгоритм бинарного (или двоичного) поиска - это один из базовых алгоритмов, который часто применяется при решении алгоритмических задач. На LeetCode на момент написания этой статьи порядка 190 задач в решении которых он используется (можно посмотреть здесь: https://leetcode.com/tag/binary-search/). Бинарный поиск разбирается во множестве статей, его идея достаточно несложная и интуитивно понятная. Однако алгоритм имеет некоторое количество "подводных камней". В этой заметке я хотел бы показать решение одной из задач с его помощью.

Для начала несколько слов о самом алгоритме. Задача, которую он решает, может быть сформулирована следующим образом: "найти в отсортированном массиве индекс элемента, значение которого соответствует заданному". Обычно массив отсортирован по возрастанию и в данной заметке мы будем предполагать, что это так и есть.

Основная идея алгоритма в том, чтобы проверить элемент в середине текущего среза массива (изначально берется весь массив). Если значение этого элемента меньше искомого, то необходимо проверить средний элемент в правой части массива, если больше, то в левой части массива. Мы будем повторять этот процесс, пока значения среднего элемента очередного среза не окажется равным искомому значению, либо больше не останется элементов (и тогда в массиве нет такого элемента). Более наглядно это видно на рисунке:

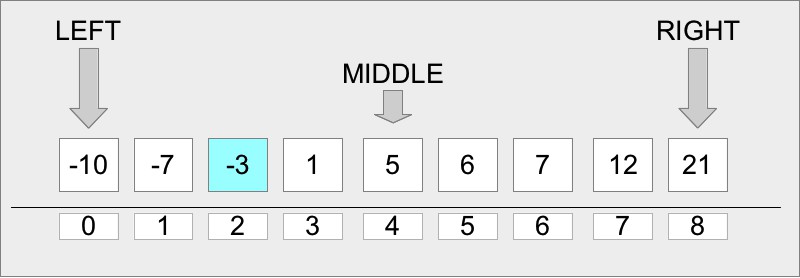
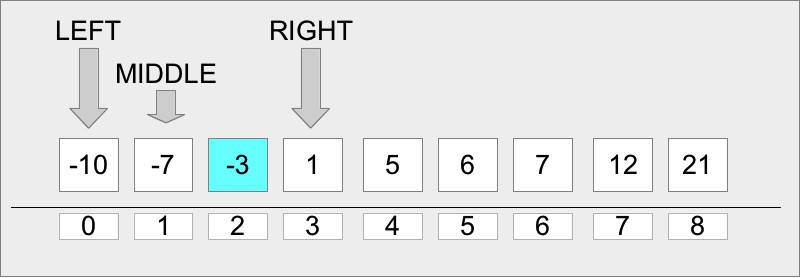
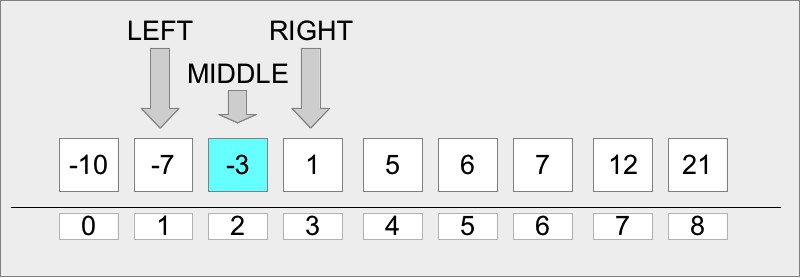
Сложность алгоритма бинарного поиска по времени выполнения O(logN) (так как мы уменьшаем срез массива на 2 на каждой итерации и проверяем только 1 элемент), и O(1) по памяти. Что касается реализации алгоритма, то обычно она выглядит следующим образом:

left, right = 0, len(array)-1
while left <= right do
	middle = (left + right) / 2
  if array[middle] > target then
  	right = middle - 1 // дальше будем проверять левую часть массива
  else if array[middle] < target then
  	left = middle + 1 // дальше будем проверять правую часть массива
  else
  	return middle // нашли элемент
  end if
end while
return -1 // элемента нет в массиве

Код на Golang можете посмотреть здесь. Есть тесты, которые включают часть corner cases. На эти случаи стоит обратить внимание и, возможно, почитать про них, например на stackoverflow (найти их описание сейчас не составляет проблем, есть много материалов как на английском, так и на русском языках).

Давайте перейдем к решению задачки с LeetCode. Возьмем для примера задачу Find Target Indices After Sorting Array. Она довольно простая, уровня easy, что позволит нам сосредоточится на одном алгоритме, а точнее его небольшой модификации. Если кратко, то суть задачи состоит в том, что нам необходимо в отсортированном массиве найти индексы всех элементов, значения которых соответствуют заданному. Есть еще одно дополнительное условие: необходимо вернуть их в порядке возрастания значений элементов массива (то есть надо сначала массив отсортировать). Таким образом, очень похоже, что нам подойдет алгоритм бинарного поиска, однако он позволяет найти индекс только одного из элементов.

Наиболее простым способом для нас будет нахождение элемента (любого) с заданным значением, затем распространение вправо и влево от него, пока значение не станет отличным с обеих сторон или мы не достигнем конца и начала массива. Однако, такой подход может привести к O(N) сложности по времени, тогда как бинарный поиск имеет сложность O(logN). Здесь может быть полезным модификация бинарного поиска, которая вернет наиболее левый элемент массива с искомым значением. Реализация алгоритма выглядит так (код на Golang можете посмотреть здесь, тесты здесь):

left, right = 0, len(array)
while left < right do
	middle = (left + right) / 2
  if array[middle] < target then
  	left = middle + 1 // дальше будем проверять правую часть массива
  else
  	right = middle // дальше будем проверять левую часть массива
  end if
end while
return left

Отлично, теперь мы сможем найти первый индекс в массиве и просто добавить все элементы начиная от него и пока не встретится элемент с отличным значением. Алгоритм будет выглядеть следующим образом (код на Golang здесь, тесты здесь):

sort(array) // сортируем массив по возрастанию ( обычно за O(NlogN) )

// бинарный поиск наиболее левого элемента
left, right = 0, len(array)
while left < right do
	middle = (left + right) / 2
  if array[middle] < target then
  	left = middle + 1 // дальше будем проверять правую часть массива
  else
  	right = middle // дальше будем проверять левую часть массива
  end if
end while

// собираем индексы элементов в результирующий массив
result = []
while left < length(array) and array[left] == target do
	append(result, left)
  left = left + 1
end while

Казалось бы, что все неплохо, но мы все еще можем получить сложность по времени O(N) в том случае, если все элементы массива содержат искомое значение. И, что может быть менее очевидным, мы можем потерять скорость на многократном выделении памяти и копировании при append.

Дальнейшим развитием решения может быть поиск индекса наиболее правого элемента массива с искомым значением. Это еще одна небольшая модификация бинарного поиска. Вот так выглядит сам алгоритм (код на Golang здесь, тесты здесь):

left, right = 0, len(array)
while left < right do
	middle = (left + right) / 2
  if array[middle] > target then
  	right = middle // дальше будем проверять левую часть массива
  else
  	left = middle + 1 // дальше будем проверять правую часть массива
  end if
end while
return right

Теперь мы можем найти оба (самый левый и самый правый) элемента за время O(logN) каждый. Код на golang можете посмотреть здесь и тесты.

Проверка кода на LeetCode дает результаты, представленные в таблице. Она включает в себя еще и результаты решения сортировкой и линейным поиском, которое не было рассмотрено в силу его простоты (код можно посмотреть здесь)

Бенчмарки на Golang с массивом из 30 одинаковых элементов, каждый из которых равен искомому дают следующие результаты

В качестве вывода хочется отметить, что знание модификаций алгоритма бинарного поиска может помочь в решении некоторых задач. Возможно оно не настолько важно и полезно, как знание исходного алгоритма, но может позволить нам сэкономить несколько миллисекунд.