Продвинутые методы Uplift-моделирования / forpes.ru

Главная
Продвинутые методы Uplift-моделирования

Продвинутые методы Uplift-моделирования +9

06.09.2022 16:37

polina_ok 0 582 Источник

Всем привет! Меня зовут Окунева Полина, я ведущий аналитик компании GlowByte команды Advanced Analytics. Сегодня я хочу рассказать о задаче Uplift-моделирования — частном случае такой большой сферы, как Causal Inference, или причинно-следственный анализ, — и методах её решения. Задачи такого типа важны во многих областях. Если вы сотрудник, например, продуктовой компании, то причинно-следственный анализ поможет сократить издержки на коммуникации с людьми, на которых она не повлияет. Если вы врач, то такой анализ подскажет, выздоровел пациент благодаря лекарству или из-за удачного стечения обстоятельств.

Какого-то полноценного гайда по продвинутым методам Uplift-моделирования я не встретила ни в русско-, ни даже в англоязычном интернете, поэтому было огромное желание структурировать информацию и поделиться ею с интересующимися.

Я предполагаю, что все, кто зашел на эту страничку, априори знакомы с постановкой задачи Uplift-моделирования и его базовыми методами. Подробно на этих методах останавливаться не будем, т. к. информации о них существует достаточно много. В частности, можно изучить цикл статей от коллег из МТС Туториал по Uplift-моделированию. Часть 1 или перейти на мой доклад в сообществе NoML, где я очень подробно рассказываю про проблематику задачи Uplift-моделирования, методы её решения и затрагиваю тему тестирования моделей.

На текущий момент существует несколько библиотек для Uplift-моделирования как на языке Python, так и на R:

Для детального рассмотрения я выбрала библиотеки EconML и CausalML, т. к. они наиболее популярны в области причинно-следственного анализа.

Цель текущей статьи — поговорить о продвинутых методах. Мы заглянем под капот каждого из них, т.к. я считаю, некорректно применять какой-то метод без четкого понимания, как он работает.

Сегодня мы рассмотрим следующие методы:

X-learner;
Domain Adaptation Learner;
R-learner;
DR-learner;
Doubly Robust Instrumental Variable (DRIV) learner.

Важно отметить до того, как перейдем к самим методам, что мы обязаны принять следующие допущения:

Stable unit treatment value assumption (SUTVA).
- Потенциальный результат от воздействия для любого сэмпла не зависит от воздействий, произведённых на другие сэмплы.
- Не существует различных уровней воздействия, ведущих к различным результатам.
Ignorability/unconfoundedness
- Для примеров с одинаковым набором фичей распределение по вариантам воздействия T, или тритмента, не зависит от потенциального результата.
Positivity
- Условная вероятность каждого значения воздействия T строго положительна:

Все перечисленные ниже методы (за исключением последнего) по итогу своей работы позволяют рассчитать значение эффекта на подгруппе CATE (Conditional Average Treatment Effect):

X-learner

Этот метод реализован в обеих библиотеках и работает следующим образом:

Шаг 1.Строим две независимые модели на контрольной и тестовой группах.

Какие модели использовать — аналитик решает сам. Главное, чтобы у класса модели была реализация методов fit() и predict().

Шаг 2. Рассчитываем разность (собственно, Uplift) между реальным значением целевой переменной и предсказанным значением (по модели). В первой строке из реального значения целевой переменной для контрольной группы вычитаем смоделированное значение целевой переменной для ровно тех же самых сэмплов (т. е. для контрольной группы) как если бы они были в тестовой. Это и есть тот эффект, который мы получим как результат определённого воздействия.

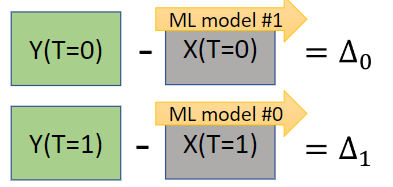
Модели также могут быть любыми, которые поддерживают методы fit() и predict().

Шаг 3. Строим две прогнозные модели на фичах сэмплов и значениях Uplift.

Т. е. итоговые модели прогнозируют сам эффект.

Шаг 4. Результаты применения двух моделей складываем с учётом веса $\epsilon(x)$ .

Вес $\epsilon(x)$ — это модель, которая в англоязычной литературе называется propensity score model. Моделью она называется потому, что прогнозирует вероятность для каждого сэмпла, исходя из его ковариат, оказаться в тестовой группе.

$\epsilon (x) = P(T=1|X=x)$

Т. о. внутри X-learner зашито обучение этой функции. По дефолту в библиотеке EconML в качестве базовой функции propensity score заложена логистическая регрессия. Но пользователь может указать абсолютно любой вариант, главное, чтобы у этого класса существовали методы fit() и predict_proba().

Domain Adaptation Learner

Метод реализован в библиотеке EconML.

Его также можно представить в виде последовательности из трёх шагов:

Шаг 1. Здесь, аналогично X-learner, строим две независимые модели на контрольной и тестовой группах.

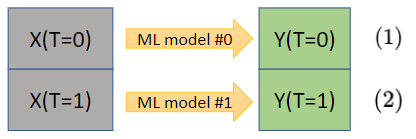
Однако, в отличие от X-learner, уже на этом этапе в моделях идёт учёт propensity score в расчете весов каждого сэмпла — модели должны уметь принимать веса на вход.

Для контрольной группы веса рассчитываются по формуле:

$Weights_{control} = \frac{\epsilon(X(T=0))}{1-\epsilon(X(T=0))} (3)$

Для тестовой:

$Weights_{test} = \frac{1-\epsilon(X(T=1))}{\epsilon(X(T=1))}(4)$

Хочу обратить внимание на одну важную особенность на примере контрольной группы. Всё, рассказанное мной ниже, очевидно из формулы, но, если не заострить внимание, то можно этот момент пропустить.

Напомню, propensity score model рассчитывает вероятность того, что объект принадлежит к тестовой группе. А теперь посмотрим на формулу (3) и место, где применяются веса — (1). При построении модели на контрольной группе больший вес будет отдаваться тем сэмплам, для которых вероятность принадлежать к тестовой группе выше. Т. е. больший вес присваивается тем объектам, которые скорее всего лежали бы в противоположной группе.

Ровно такие же рассуждения можно провести для построения модели по данным тестовой группы: больший вес отдается тем элементам, которые наиболее вероятно, опираясь на их фичи, лежали бы в контрольной группе.

Далее всё как в X-learner.

Шаг 2. Считаем разности (Uplift)

Шаг 3. Строим модель прогноза эффекта по ковариатам сэмпла

В итоге видим, что финальная модель прогнозирует на выходе сам Uplift.

R-learner

Прежде чем перейти к самой модели, мы пробежимся немного по теоретической части.

Вначале введём определения двух функций:

$\epsilon(x) = P(T=1|X=x)$ — уже знакомая нам propensity score model, $\mu(x) = E(Y(t)|X=x), t=\{0, 1\}$ — функция, выражающая математическое ожидание целевой переменной при фиксированных ковариатах для каждого из вариантов воздействий.

Обозначим через $\xi_{i}(t)$ разность между реальным значением, которое мы имеем с эксперимента, и спрогнозированный значением целевой переменной (с учётом описанных выше моделей):

$\xi_{i}(t)=Y_{i}(t) - ( \mu_{0}(X_{i}) + t \cdot \tau(X_{i})) \Rightarrow Y_{i}(t) = ( \mu_{0}(X_{i}) + t \cdot \tau(X_{i})) + \xi_{i} (t) (5)$

Т. к. предполагается выполнение свойства unconfoundedness (его определение можно найти в начале статьи), то:

$E(\xi_{i} (T_{i})|X_{i}, T_{i})=0$

Далее введём следующее обозначение: $m(x) = E(Y|X=x) = \mu_{0}(X_{i}) + \epsilon(X_{i})\cdot \tau(X_{i})(6)$

Отличие между выражениями и заключается в следующем: в выражении используется переменная t — реальный факт воздействия или его отсутствия, в выражении подставляется результат функции ϵ(x). Т. е., несмотря на то, что объект, например, был в контрольной группе, значение ϵ(x) могло быть близко к 1.

Рассчитаем разность, где выражение для $Y_{i}(t)$ возьмём из, а из :

$Y_{i} - m(X_{i}) = ( \mu_{0}(X_{i}) + T_{i} \cdot \tau(X_{i})) + \xi_{i} (t) - (\mu_{0}(X_{i}) + \epsilon(X_{i})\cdot \tau(X_{i}))$

Сократив все одинаковые слагаемые, придём к следующему выражению:

$Y_{i} - m(X_{i}) = (T_{i} - \epsilon(X_{i}))\cdot\tau(X_{i}) + \xi_{i} (t)$

Все так же, исходя из допущения unconfoundedness, мы понимаем, что функция $\tau(X_{i})$ должна быть такой, чтобы минимизировать выражение:

Чтобы оптимизатор мог корректно работать, сделаем функцию выпуклой и не зависящей от знака выражения. Стандартно это делается следующим образом:

$\tau = \arg \min_{\tau}(E((Y_{i} - m(X_{i})) - (T_{i} - \epsilon(X_{i}))\cdot\tau(X_{i}))^2)$

Добавив регуляризационный член и перейдя к конкретному решению задачи, имеем выражение:

$\tilde \tau = \arg \min_{\tau} (\frac{1}{n}\sum_{i=1}^{n}[(Y_{i} - m(X_{i})) - (T_{i} - \epsilon(X_{i}))*\tau(X_{i})]^2 + \Lambda_{n}(\tau))$

Теперь перейдём непосредственно к самому алгоритму R-learner, который реализован в CausalML.

Шаг 1. Задача аппроксимации.

Разделяем данные на несколько фолдов и строим функции с кросс-валидацией по всем фолдам.

$\epsilon(x) = P(T=1|X=x)$
$\mu(x) = E(Y(t)|X=x), t=\{0, 1\}$

Шаг 2. Задача оптимизации.

Подбираем параметры функции $\tau$ таким образом, чтобы они минимизировали сумму двух слагаемых: функции $L(\tau)$ и регуляризатора $\Lambda(\tau)$ , который стандартно работает на ограничение сложности функции $\tau$ .

$\tau = \arg \min_{\tau}(\tilde L_{n}(\tau) + \Lambda_{n}(\tau))$ $\tilde L_{n}(\tau) = \frac{1}{n}\sum_{i=1}^{n}[(Y_{i} - \hat \mu_{-q(i)}(X_{i})) - (T_{i} - \hat \epsilon_{-q(i)}(X_{i}))*\tau(X_{i})]^2,$

где $\hat \mu_{-q(i)}, \hat \epsilon_{-q(i)}$ — прогноз значений без учёта данных из фолда, к котрому принадлежит объект .

DR-learner

Метод реализован в CausalML, работа в нём происходит в три шага.

Шаг 1. Исходный датасет делится на три части:

На первой части строится модель propensity score model.
На второй части данные разделяем на подсэмплы — контрольная и тестовая группы, и на каждой из подчастей строится своя прогнозная модель (outcome regression model), которая предсказывает целевую переменную.
Третья часть на Шаге 1 остается незадействованной $(X_{3}, Y_{3})$ .

Шаг 2. В этом этапе участвуют незадействованная в Шаге 1 третья часть — $(X_{3}, Y_{3})$ . Происходит расчёт значения функции $\tau_{3}(X_{3}, Y_{3})$ , в которой участвуют модели, полученные на Шаге 1, — propensity score model и outcome regression model, в которые, в качестве переменной и отклика , подставляются $X_{3}$ и $Y_{3}$ .

$\tau_{3} = \frac {T - \tilde\epsilon(X)}{\tilde\epsilon(X)(1-\tilde\epsilon(X))}\cdot(Y - \mu_{(1)}(X)\cdot T - \mu_{(0)}(X)\cdot (1-T)) + \mu_{(1)}(X) - \mu_{(0)}(X)$

Далее части на Шаге 1 меняются местами и соответственно те же самые модели, но строятся на других долях исходного датасета.

Аналогично рассчитываем $\tau_{1}(X_{1}, Y_{1})$ и $\tau_{2}(X_{2}, Y_{2})$ .

Шаг 3. Рассчитываем итоговое значение функции $\tau$ как среднее арифметическое трёх значений — $\tau_{1}, \tau_{2}, \tau_{3}:$

$\tau = \frac{\tau_{1}+\tau_{2}+\tau_{3}}{3}$

Doubly Robust Instrumental Variable (DRIV) learner

И последний метод на сегодня. Он стоит немного особняком от остальных, т. к. позволяет рассчитать не CATE, а LATE — local average treatment effect.

Существуют ситуации, в которых невозможно заранее задать распределение по T: факт воздействия — выбор, который стоит перед самим пользователем. Но мы, как экспериментаторы, можем подтолкнуть пользователя к какому-то решению.

Как это выглядит на примере: допустим, магазин проводит акцию и хочет оценить эффект от этой кампании. Сложность оценки в том, что акция не таргетированная. Т.- е. поучаствовать в ней может любой человек (в зависимости от его личного решения) — это определяет переменная T. Однако кураторы акции могут проводить или не проводить акцию в конкретном магазине — за это отвечает переменная Z.

Эффект рассчитывается следующим образом:

$\tau_{complier} = \frac{E(Y|Z=1) - E(Y|Z=0)}{E(T|Z=1) - E(T|Z=0)}$

В числителе — разность двух математических ожиданий целевой переменной при фиксированных значениях Z, а в знаменателе — разность двух математических ожиданий факта воздействия, или участия в какой-то акции, при фиксированных значениях Z.

Сам алгоритм можно разбить на три этапа.

Шаг 1. Делим датасет на 3 части.

На первой части $(X_{1}, T_{1}, Z_{1})$ строим две модели propensity score, т. е. фиксируем $Z_{1}$ и на соответствующих $X_{1}$ строим модель, прогнозирующую $T_{1}$ , — $\epsilon_0, \epsilon_{1}$ .

На второй части $(X_{2}, Y_{2}, Z_{2})$ строим две модели, прогнозирующие целевую переменную, т. е. фиксируем $Z_{2}$ и строим зависимость $Y_{2}$ от $X_{2}$ — $\mu_{(0)}, \mu_{(1)}$ .

Третья часть — $(X_{3}, Y_{3}, Z_{3}, T_{3})$ — остается незадействованной.

Шаг 2. Работаем с третью частью — $(X_{3}, Y_{3}, Z_{3}, T_{3})$ . Это шаг оптимизации, на котором подбираем параметры функции $\tau_{3}$ так, чтобы функция потерь — $L_{\tau}$ — принимала свой минимум (теоретически который есть 0):

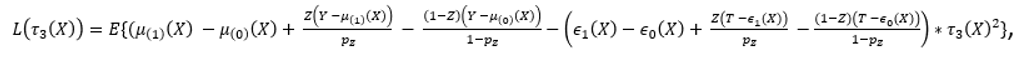
где $p_{z}$ — вероятность каждого участника попасть в ту или иную группу, которую экспериментатор задаёт самостоятельно.

Если рассмотреть подробнее, что стоит в скобках под функцией математического ожидания, то можно увидеть, что это два варианта выражения эффекта. Один вариант мы получаем через разность двух матожиданий целевой переменной для контрольной и тестовой групп с поправкой на разницу между реальным значением целевой переменной и матожиданием целевой переменной. Второй вариант — тот же эффект, только выраженный через функцию $\tau$ .

В результате шага оптимизации коэффициенты $\tau_{3}(X_{3})$ подобраны так, что происходит минимизация функции потерь $L(\tau_{3}(X_{3}))$ . В финале шага 2 рассчитываем значение $\tau_{3}(X_{3})$ .

Аналогично проводим расчёт для $\tau_{1}(X_{1})$ и $\tau_{2}(X_{2})$ .

Шаг 3. На последнем шаге усредняем значения функций $\tau$ , полученные по всем фолдам.

$\tau = \frac{\tau_{1} + \tau_{2} + \tau_{3}}{3}$

Вместо заключения

Ситуации при работе в сфере Causal Inference можно разделить на два типа:

Eсть возможность управлять данными, и в таком случае подбираются подходящие данные к методу. Например, частным случаем являются A/B тесты, в которых очень важным пунктом является разделение на сопоставимые группы.
Данными управлять не представляется возможным, и идёт подбор метода к данным. Именно здесь и применяется Uplift-моделирование. Частью таких методов являются те, что были рассмотрены в статье выше. Их ключевой особенностью является участие во всех них propensity score model. Именно с помощью этой функции происходит учёт смещения при определении объекта (в момент эксперимента) к той или иной группе — контрольной или тестовой.

Глобально вторая группа сегодняшними методами не ограничивается — существуют, например, такие методы, в которых учитываются переменные confounder`ы. Но об этом уже в другой раз.

Всех приглашаем в наше сообщество noML, где мы активно обсуждаем различные темы вокруг ML и продвинутой аналитики в реальных бизнес-задачах:

Канал новостей

Чат

Также предлагаем посмотреть запись нашего доклада, на базе которого написана статья.