22.09.2022 14:03
rotor 1 1500 Источник

У задач классификации, в отличие от задач регрессии, есть одно очень приятное свойство:
большинство ML алгоритмов решения задач классификации выдают не просто ответ, а некоторую оценку уверенности модели в ответе. То есть помимо метрик самой модели мы обладаем оценкой вероятности для конкретного ответа на конкретном примере. Это здорово помогает в принятии решений.

Неправда ли хотелось бы иметь что-то такое и для задач регрессии?

В задачах классификации почти все алгоритмы машинного обучения выдают нам некоторое число p в интервале [0, 1].

Это число можно рассматривать, с одной стороны, как оценку вероятности того, что метка рассматриваемого примера относится к положительному классу. С другой стороны, мы можем считать, что наша модель выдаёт распределение вероятностей для меток класса: пара чисел (1-p, p), где 1-p — оценка вероятности негативного класса и p — оценка вероятности позитивного класса. Кроме того, это же число p является и средним по модельному распределению: p = (1-p) \cdot 0 + p \cdot 1.

Таким образом, в случае задач классификации мы обладаем полной информацией о распределении для каждого конкретного примера. В силу тривиальности самого распределения, чаще всего, эта информация используется просто для оценки уверенности. Но даже в таком простом случае дополнительная информация существенно обогащает возможные варианты использования модели.

Любой алгоритм машинного обучения, так или иначе, "выучивает" заложенное в обучающей выборке распределение. И в этом отношении задачи регрессии ничуть не хуже задач классификации.

Давайте попытаемся понять, чего же мы хотим от моделей регрессии: что бы они стали такими же гибкими в применении как и модели классификации?

При наивном взгляде может показаться, что было бы неплохо иметь некоторый ответ модели, число v и некоторую оценку уверенности в ответе, число p в интервале [0, 1]. Но как интерпретировать эту уверенность? Если интерпретировать её как оценку вероятности того, что v является ответом, то какова оценка вероятности для v + \epsilonдля малого \epsilon?

Дело в том, что для непрерывно распределённой величины x мы не можем оценивать вероятность того, что x = v. Точнее, вероятность того что наша непрерывно распределённая величина x равна конкретному значению всегда будет равна нулю.

Но вот оценка принадлежности к интервалу имеет смысл. То есть вероятность принадлежности к интервалу [v-\epsilon, v+\epsilon]вполне может быть оценена и будет иметь вполне определённый смысл.

Все эти наводящие соображения приводят нас к мысли, что оценивать нам нужно не некоторую абстрактную уверенность, а вполне конкретную плотность распределения. То есть вероятность попадания ответа в любой допустимый интервал из области значений моделируемой величины.

Знание распределения для каждого примера, в таком случае, даст нам гораздо больше возможностей для принятия решений при использовании модели:

  • оценить уверенность прогноза в каждой конкретной точке. Для этого можно использовать дисперсию распределения или любые другие подходящие статистические характеристики;

  • найти не только среднее значение, но и наиболее вероятное значение ответа;

  • определить доверительный интервал возможных значений оценки ответа модели;

  • вычислить любые характеристики распределения, определяемые конкретной задачей и позволяющие более взвешенно и точно принимать решения на основе прогноза модели.

Хорошо. Допустим, у нас есть модель, выдающая нам каким-то образом плотность вероятности или функцию распределения. Но ведь первоочередная наша цель — это именно число. Сам прогноз.

Имея функцию распределения, мы можем получить конкретный прогноз, просто взяв среднее: матожидание.

То есть мы вообще ничего не теряем.

Теперь, когда мы знаем чего мы хотим, давайте решим как мы этого достигнем.

Для простоты рассуждений можем ограничиться случаем, когда нам предстоит строить модель для одномерных величин. То есть когда и наш таргет является просто числом, а не вектором, и пространство признаков тоже одномерно.

У нас есть два пути:

  1. Построить модель, генерирующую плотность распределения.

  2. Построить модель, генерирующую функцию распределения.

Я предлагаю моделировать функцию распределения. И на это у меня есть несколько причин:

  • Плотность распределения — величина дифференциальная, а функция распределения — интегральная. Это означает, что функция распределения статистически более устойчива.

  • Плотность распределения должна удовлетворять одному очень сильному ограничению: её интеграл по всей области значений должен быть равен 1:

\int_{-\infty}^{\infty}\rho(y) dy = 1

Последнее ограничение кажется будет очень сложно удовлетворить. Разумеется, мы всегда можем выполнить нормировку, либо как-то модифицировать модель, наложив на неё дополнительные ограничения в процессе обучения. Но это не тот путь, которым я хотел бы идти.


Я допускаю, что кто-то из читателей этой статьи может предложить свой вариант моделирования распределения, основанный именно на плотности. Такой подход имеет право на жизнь.

На функцию распределения тоже накладываются ограничения. Но эти ограничения проще удовлетворить.

Функция распределения должна быть в интервале [0, 1], она должна быть монотонной и её предельные значения на минус бесконечности и на бесконечности должны быть 0 и 1, соответственно:

M(x, t) \in [0, 1],\, \forall t \in \mathbb{R}t_1 \leqslant t_2 \Rightarrow M(x, t_1) \leqslant M(x, t_2)\lim\limits_{t \to -\infty} M(x ,t) = 0; \lim\limits_{t \to +\infty} M(x ,t) = 1

Подход, который я предлагаю ниже, выстроен именно таким образом, что бы моделируемая функция распределения была как можно ближе к истиной функции распределения и при этом удовлетворяла наложенным выше ограничениям.

И хотя по построению наложенные выше ограничения должны удовлетворяться, гарантировать это невозможно. И проверку этих ограничений нужно обязательно вынести на этап валидации модели.

Итак, наше знание об истинном распределении представлено для нас в виде обучающей выборки примеров, пар признак — таргет:

\{(x_i, y_i)\}_{i=1}^N,

где, x_i — признак и y_i — таргет.
Эта обучающая выборка порождает набор тривиальных функций распределения \{F_i\}_{i=1}^N:

F_i(t) = \begin{cases}1, & t \geqslant y_i \\0, & t < y_i \\\end{cases}

Наша цель построить такую модель M(x, t), которая будет принимать в качестве аргумента признак xи число t, которое будет аргументом функции распределения для конкретного признака и возвращать число M(x, t) \in [0, 1], удовлетворяя при этом наложенным выше ограничениям.

При этом наша модель должна обобщать представленные тривиальные функции распределения \{F_i\}_{i=1}^N.

То есть вместо того, чтобы строить модель на обучающем наборе \{(x_i, y_i)\}_{i=1}^N, нам нужен новый обучающий набор. Такой, чтобы можно было обучить M(x, t) , и чтобы он "ложился" на наш набор тривиальных функций распределения \{F_i\}_{i=1}^N.

Алгоритм

По заданному обучающему набору\{(x_i, y_i)\}_{i=1}^N признаковx_i и таргетовy_iдля каждой пары (x_i, y_i) строим новый набор признаков (x_i, t_{i, j})и таргетов u_{i, j}.

Для этого случайно берём Kточек \{t_j\}_{j=1}^Kиз равномерного распределения в области значений таргета Y (\{y\}_i \subset Y). А u_{i, j}строим следующим образом:

u_{i j} = \begin{cases} 1, & t_j \geqslant y_i \\ 0, & t_j < y_i \\ \end{cases}

Полученные таким образом для каждой пары (x_i, y_i) наборы ((x_i, t_{i, j}), u_{i, j})объединяем в единый обучающий набор (и при необходимости перемешиваем) и строим на новой выборке модель как для обычной задачи регрессии.

Новыми признаками будут пары (x_i, t_{i, j}), а новыми таргетами числа u_{i, j}.

Замечание. Точки t_{i, j} лучше брать так, чтобы было равное количество точек u_{i, j} < y_i и u_{i, j} > y_i.

Пример

В качестве иллюстрации я подготовил блокнот.

В качестве базовой закономерности возьмём функцию

f(x) = 1 - x^2 + \frac{3}{2} x - \sin(2 \pi x^2)

на отрезке x \in [0, 1]. И добавим к ней нормальный шум \mathcal{N}(f(x), \sigma(x)), где \sigma(x) = 0.05 + \frac{x}{2}.

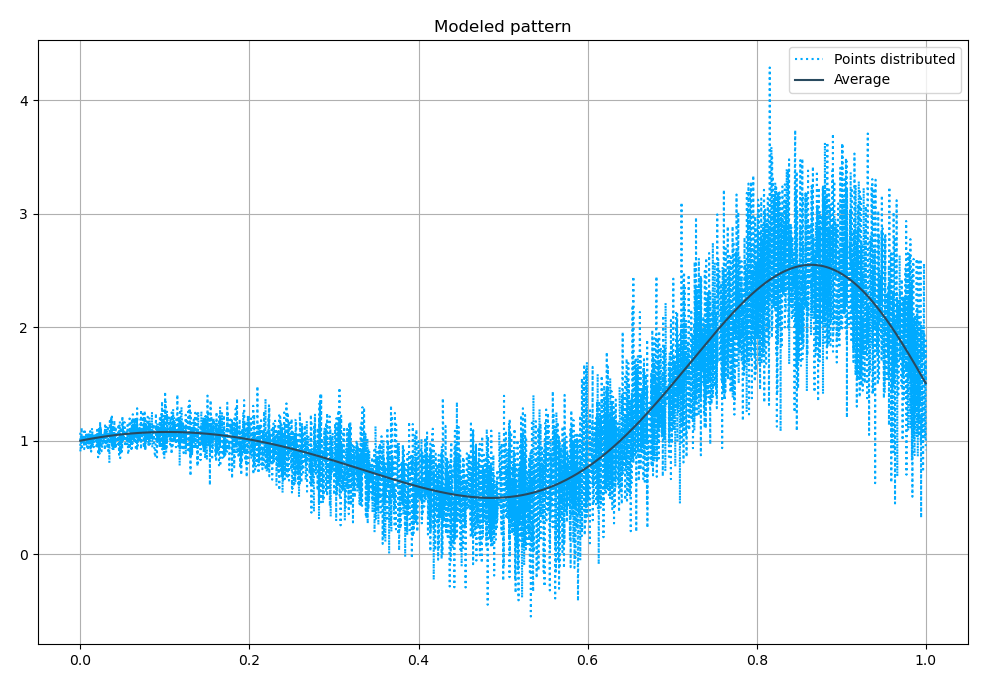
Решение обычной задачи регрессии даёт ожидаемое схождение прогнозной величины и среднего, определяемого функцией f(x):

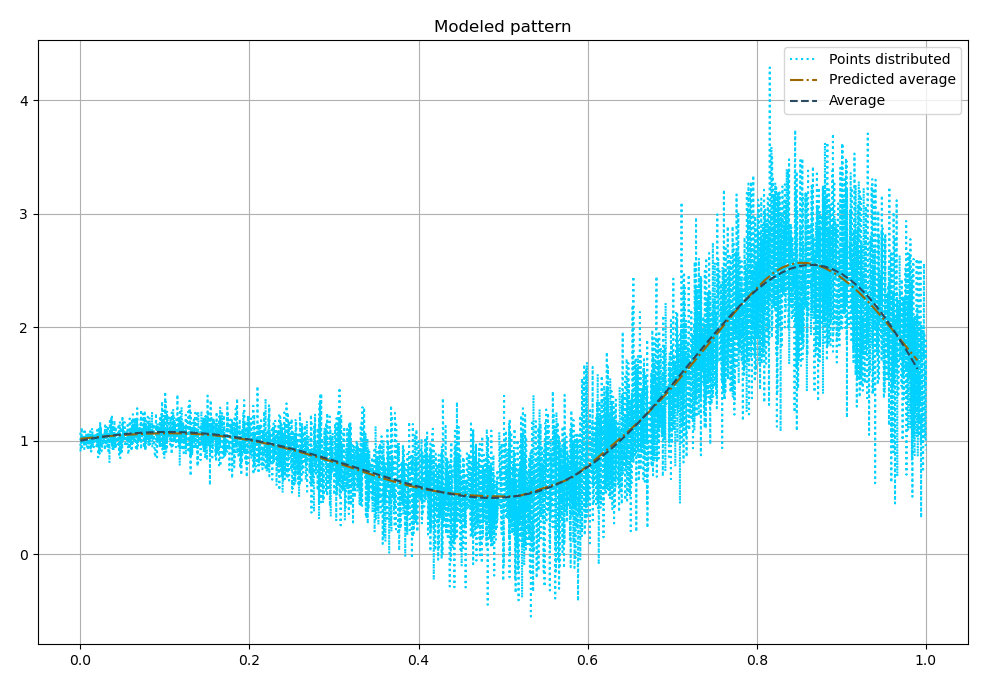
Теперь построим модель, порождающую функции распределения:

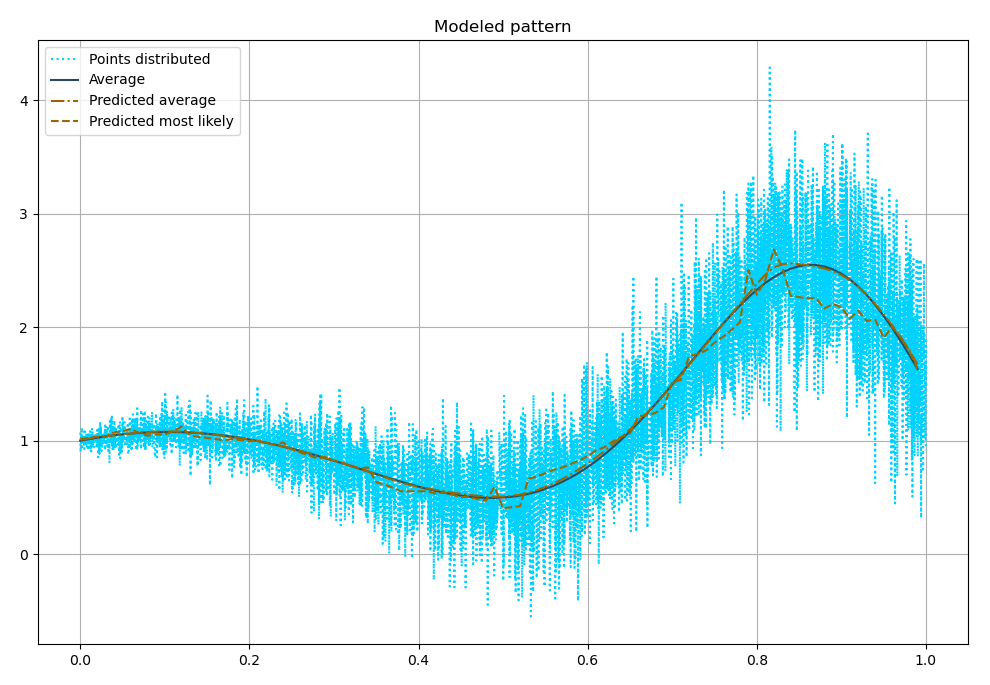
Как видно, средние хорошо сходятся к истинным средним. А вот наиболее вероятные, в нашем случае, имеют некоторую вариативность.

Вот пример истиной и модельной функций распределения для одной из точек:

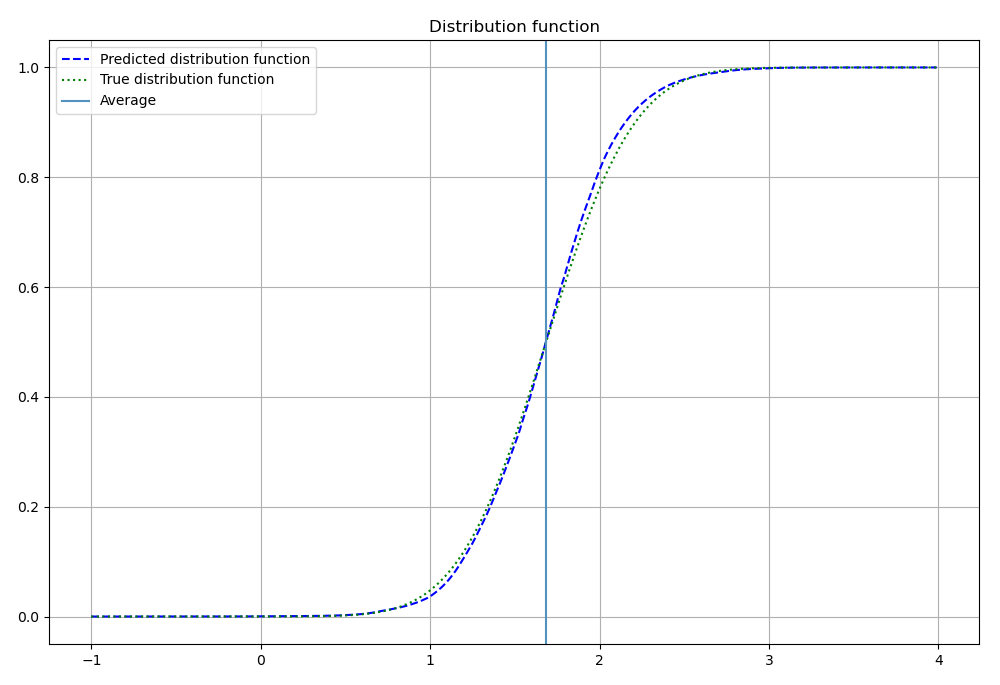
А это все функции распределения для всех точек:

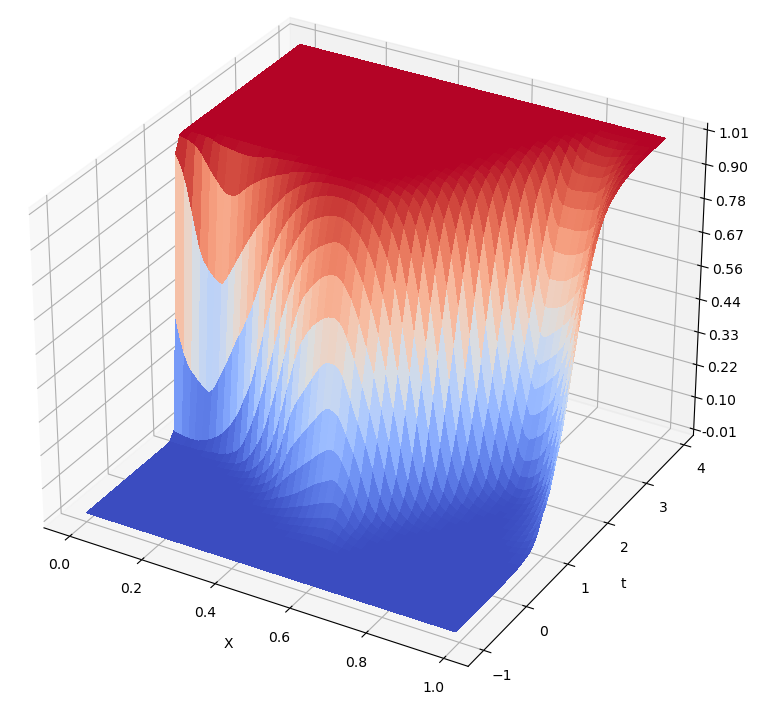
Недостатки

Главный и, как мне кажется, единственный недостаток — это существенное возрастание необходимых для обучения модели вычислительных ресурсов.

Действительно. Ведь теперь нам нужно не просто выучить средние, но и целиком распределения. Это возможно потребует более ёмкую модель.

Кроме того, мы в Kраз увеличили объём набора данных. А в случае, когда наше пространство признаков не одномерное, а d-мерное, объём датасета возрастёт в K^dраз, что может оказаться весьма существенным.

PS

Ссылка на пример реализации алгоритма.

Я постарался сделать изложение максимально простым и понятным для людей, незнакомых с математикой. Если вы предпочитаете более строгий стиль, то вот ссылка для вас.

Буду очень признателен, если кто-то сможет предоставить мне endorsement на arXiv в секцию cs.IT. https://arxiv.org/auth/endorse?x=ZZDXS8

Комментарии (1)


  1. promsoft
    22.09.2022 17:04
    #24758812

    Обычно эту задачу решают так: кроме целевой переменной предсказывают еще и разброс для каждой точки (те у нас два предикта - центр распределения и дисперсия).