12.10.2022 12:00
Nikuson 2 4700 Источник

Метод обратной диффузии поистине является самым нашумевшим в этом году методом генерации изображений нейросетями. Его используют: DALLE 2, Midjourney, imagen и другие актуальные модели 2022 года.

В данной статье мы подробно изучим, что под капотом самых современных генеративных моделей и даже напишем небольшую свою.

Под катом будет много кода, программирования, математики, в общем — всё, как вы любите.

Диффузионные модели являются генеративными моделями, что означает использование их для создания данных, подобных тем данным, на которых они обучаются.
image

Общая концепция обучения:

  1. Берём начальное изображение
  2. Итеративно добавляем Гаусовский шум, пока от исходного ничего не останется, только каша из пикселей
  3. Обучите модель шумоподавления приводить эту кашу к результату, похожему на исходное изображение

Общая концепция генерации: создайте чистый Гаусовский шум и дайте его обученной модели шумоподавления, чтобы получить абсолютно новое изображение

▍ Импортируем всё, что нам потребуется


!pip install datasets &>> install.log

from datasets import load_dataset
from PIL import Image
import torch.nn.functional as F
import os
from tqdm.notebook import tqdm
import torch
import numpy as np


def img_to_tensor(im):
  return torch.tensor(np.array(im.convert('RGB'))/255).permute(2, 0, 1).unsqueeze(0) * 2 - 1

def tensor_to_image(t):
  return Image.fromarray(np.array(((t.squeeze().permute(1, 2, 0)+1)/2).clip(0, 1)*255).astype(np.uint8))

def gather(consts: torch.Tensor, t: torch.Tensor):
    c = consts.gather(-1, t)
    return c.reshape(-1, 1, 1, 1)


▍ Данные


Готовьте свои блокноты colab для запуска кода, будем учиться на практике (Советую включить GPU). Для начала загрузим набор данных CIFAR-10 c 60 000 изображениями 32×32 пикселя и некоторые библиотеки с нужными функциями.

Конечно, диффузионные модели могут обрабатывать изображения любого разрешения, но для начала нам подойдёт и такой:

image

# Скачать и загрузить набор данных
cifar10 = load_dataset('cifar10')

image = Image.new('RGB', size=(32*5, 32*2))
for i in range(10):
  im = cifar10['train'][i]['img']
  image.paste(im, ( (i%5)*32, (i//5)*32 ))
image.resize((32*5*4, 32*2*4), Image.NEAREST)


▍ Шум


Для создания набора шумных изображений нам потребуется наложить Гаусовский шум на наш набор данных. Мы устанавливаем «график отклонений», он указывает, сколько шума мы хотим добавить на одном шаге.

По формуле:

$q(xt|xt−1)=N(xt;1−βt−−−−−√xt−1,βtI)q(x1:T|x0)=∏Tt=1q(xt|xt−1)$


Всё просто. Мы смешиваем xt−1 с Гаусовским шумом, определяемым βt
Ключевая идея в том, что после нескольких шагов шум будет складываться.

n_steps = 100
beta = torch.linspace(0.0001, 0.04, n_steps)

def q_xt_xtminus1(xtm1, t):
  mean = gather(1. - beta, t) ** 0.5 * xtm1 # √(1−βt)*xtm1
  var = gather(beta, t) # βt
  eps = torch.randn_like(xtm1) # Шум в форме xtm1
  return mean + (var ** 0.5) * eps

# Показать на разных этапах
ims = []
start_im = cifar10['train'][3]['img']
x = img_to_tensor(start_im).squeeze()
for t in range(n_steps):

  # Сохранение изображения каждые 20 шагов, чтобы показать прогресс
  if t%20 == 0:
    ims.append(tensor_to_image(x))
  
  # Вычислить Xt с учётом Xt-1 (т.е. x из предыдущей итерации)
  t = torch.tensor(t, dtype=torch.long) # t как тензор
  x = q_xt_xtminus1(x, t) # Изменение x, используя нашу функцию выше

# Отображение изображений
image = Image.new('RGB', size=(32*5, 32))
for i, im in enumerate(ims):
  image.paste(im, ((i%5)*32, 0))
image.resize((32*4*5, 32*4), Image.NEAREST)


image

Но мы будем делать это более целесообразным способом. Давайте попробуем использовать приём репараметризации, который позволяет нам получить xt любого x0 сразу:

$q(xt|x0)=N(xt;α¯t−−√x0,(1−α¯t)I) where α¯t=∏Ti=1αi$


Статья про репараметризацию
Код не так страшен, как может показаться глядя на формулу:

n_steps = 100
beta = torch.linspace(0.0001, 0.04, n_steps)
alpha = 1. - beta
alpha_bar = torch.cumprod(alpha, dim=0)

def q_xt_x0(x0, t):
  mean = gather(alpha_bar, t) ** 0.5 * x0 # теперь alpha_bar
  var = 1-gather(alpha_bar, t) # (1-alpha_bar)
  eps = torch.randn_like(x0)
  return mean + (var ** 0.5) * eps

# Показать на разных этапах
ims = []
start_im = cifar10['train'][3]['img']
x0 = img_to_tensor(start_im).squeeze()
for t in [0, 20, 40, 60, 80]:
  x = q_xt_x0(x0, torch.tensor(t, dtype=torch.long))
  ims.append(tensor_to_image(x))

image = Image.new('RGB', size=(32*5, 32))
for i, im in enumerate(ims):
  image.paste(im, ((i%5)*32, 0))
image.resize((32*4*5, 32*4), Image.NEAREST)


Заметьте, что теперь нам не требуется использовать *for t in range*

▍ Шумоподавление. U-NET


Единственное требование к нашей архитектуре Шумоподавления — чтобы её вход и выход были одинаковыми размерами. Именно поэтому неудивительно то, что модель диффузии изображения часто реализуется с архитектурами, подобными U-Net.

U-NET представляет собой архитектуру преобразования изображения в изображение. Чаще всего её используют для сегментации биомедицинских изображений, но и нам пригодилась.

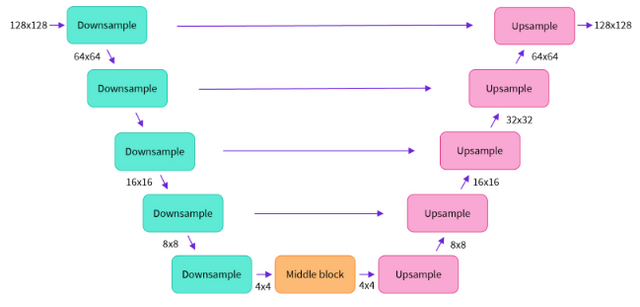
image

Архитектура передаёт информацию с ранних уровней с высоким разрешением — в более поздние уровни. «Ярлык» позволяет сети использовать подробные функции исходного изображения, а также захватывать более высокоуровневую семантику из глубоких слоёв.

Диффузионные нейросети используют архитектуру U-NETс одним дополнением: TimeEmbedding
TimeEmbedding кодирует временной шаг (t) и позволяет модели использовать это в качестве информации для кондиционирования, передавая её в середине сети.

Если вы копируете код по ходу статьи, скопируйте код U-NET отсюда. (Но в любом случае в конце будет ссылка на colab со всем кодом из статьи)

▍ Обучение


Теперь мы должны научить модель нам нужно обучить её предсказывать шум с учётом xt и t. Но почему мы возимся с этим, а не генерируем шумное изображение напрямую?

В основном просто из-за удобства. Шум хорошо масштабируется со средним значением, равным нулю, и это хорошо подходит для моделирования с помощью нейронной сети. Настроим нашу функцию q_xt_x0 так, чтобы она возвращала как изображение с шумом (xt), так и сам шум, который будет целью, которую пытается создать наша модель.

x = torch.randn(10, 3, 32, 32)
t = torch.tensor([50.], dtype=torch.long)
unet = UNet()
model_output = unet(x, t)
model_output.shape

# Создайте модель
unet = UNet(n_channels=32).cuda()
 
# Настройка параметров
n_steps = 100
beta = torch.linspace(0.0001, 0.04, n_steps).cuda()
alpha = 1. - beta
alpha_bar = torch.cumprod(alpha, dim=0)
 
# возвращаем шум
def q_xt_x0(x0, t):
  mean = gather(alpha_bar, t) ** 0.5 * x0
  var = 1-gather(alpha_bar, t)
  eps = torch.randn_like(x0).to(x0.device)
  return mean + (var ** 0.5) * eps, eps # также возвращает шум
 
# Тренировочные параметры
batch_size = 128
lr = 3e-4 # Скорочть обучение, это значение я называю это константой Карпати
 
losses = [] # Сохранение потери для построения графика
 
dataset = cifar10['train']
optim = torch.optim.AdamW(unet.parameters(), lr=lr) # Оптимизатор
 
for i in tqdm(range(0, len(dataset)-batch_size, batch_size)): # Просмотр набора данных
  ims = [dataset[idx]['img'] for idx in range(i,i+batch_size)]
  tims = [img_to_tensor(im).cuda() for im in ims] # Преобразование в тензоры
  x0 = torch.cat(tims)
  t = torch.randint(0, n_steps, (batch_size,), dtype=torch.long).cuda()
  xt, noise = q_xt_x0(x0, t)
  pred_noise = unet(xt.float(), t)
  loss = F.mse_loss(noise.float(), pred_noise)
  losses.append(loss.item())
  optim.zero_grad()
  loss.backward()
  optim.step()

После обучения можем отобразить график ошибок, это самое красивое, что я видел за день:

from matplotlib import pyplot as plt
plt.plot(losses)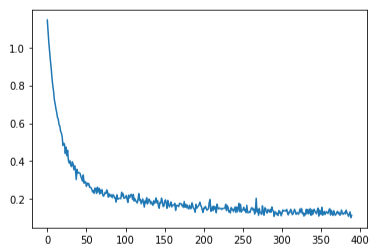

image

▍ Шумоподавление


Теперь нам нужно определить шумоподавление pθ(xt−1|xt).

Мы используем нашу модель для прогнозирования шума, а затем «отменяем» шаги прямого шума по одному за раз, чтобы перейти от изображения, представляющего собой чистый шум, к изображению, которое (надеюсь) выглядит похоже на реальное изображение:

def p_xt(xt, noise, t):
  alpha_t = gather(alpha, t)
  alpha_bar_t = gather(alpha_bar, t)
  eps_coef = (1 - alpha_t) / (1 - alpha_bar_t) ** .5
  mean = 1 / (alpha_t ** 0.5) * (xt - eps_coef * noise)
  var = gather(beta, t)
  eps = torch.randn(xt.shape, device=xt.device)
  return mean + (var ** 0.5) * eps 
 
x = torch.randn(1, 3, 32, 32).cuda() # Создадим рандомный шум
ims = []
for i in range(n_steps):
  t = torch.tensor(n_steps-i-1, dtype=torch.long).cuda()
  with torch.no_grad():
    pred_noise = unet(x.float(), t.unsqueeze(0))
    x = p_xt(x, pred_noise, t.unsqueeze(0))
    if i%24 == 0:
      ims.append(tensor_to_image(x.cpu()))
 
image = Image.new('RGB', size=(32*5, 32))
for i, im in enumerate(ims[:5]):
  image.paste(im, ((i%5)*32, 0))
image.resize((32*4*5, 32*4), Image.NEAREST)

image

Мы тренируемся здесь только со 100 шагами шума, и, возможно, модель видит изображения, в которых есть хотя бы небольшая структура, но это далеко не идеально, отчасти из-за маленького размера модели. Если мы начнём с изображения с наполовину зашумлённого, может ли оно исправить его до чего-то похожего на оригинал?

horse = cifar10['train'][4]['img']
x0 = img_to_tensor(horse)
x = torch.cat([q_xt_x0(x0.cuda(), torch.tensor(50, dtype=torch.long).cuda())[0] for _ in range(10)] )
example_start = q_xt_x0(x0.cuda(), torch.tensor(50, dtype=torch.long).cuda())[0]
print(x.shape)
ims = []
for i in range(50, n_steps):
  t = torch.tensor(n_steps-i-1, dtype=torch.long).cuda()
  with torch.no_grad():
    pred_noise = unet(x.float(), t.unsqueeze(0))
    x = p_xt(x, pred_noise, t.unsqueeze(0))
 
for i in range(10):
  ims.append(tensor_to_image(x[i].unsqueeze(0).cpu()))
 
image = Image.new('RGB', size=(32*5, 32*2))
for i, im in enumerate(ims):
  image.paste(im, ((i%5)*32, 32*(i//5)))
  if i==0:image.paste(tensor_to_image(example_start.unsqueeze(0).cpu()), ((i%5)*32, 32*(i//5)))
image.resize((32*4*5, 32*4*2), Image.NEAREST)

image

▍ Как работают диффузионные Text-to-image?


Обученная языковая модель передаёт в Unet некоторую кодировку текста (чаще из предварительно обученной языковой модели) и передаётся в качестве дополнительной обусловливающей информации.
Также мы можем попробовать встроить нужную информацию аналогично тому, как мы кодировали t. Например, можно это сделать через эмбендинги CLIP, как это сделано в DALLE 2.

▍ Выводы


Вы смогли погрузиться в удивительный мир диффузионных моделей и посмотрели на них изнутри, разобрав на код все основные принципы современных генеративных нейросетей.

Надеюсь, вам это показалось интересным и увлекательным.

Потыкать код и обучить модельку можно в этом колабе.

image
RUVDS | Community в telegram и уютный чат

Комментарии (2)


  1. lgorSL
    13.10.2022 20:35
    #24817722

    Как статья соотносится с вот этой ссылкой? https://colab.research.google.com/drive/1NFxjNI-UIR7Ku0KERmv7Yb_586vHQW43?usp=sharing#scrollTo=g7btoXL7Im7M


  1. Nikuson Автор
    14.10.2022 18:51
    #24822262

    36 плюсиков ????