Я занимаюсь написанием различных мелодий в разных жанрах довольно давно, но только недавно решил соотнести это занятие с научным подходом.
Что, если существует формула нахождения частоты любой выбранной ноты на любом аккорде? Что ж, углубившись в построение частот нот и настройку музыкальных инструментов, можно выяснить, что, во-первых, лучше использовать алгоритм, а во-вторых - всё будет зависеть от того, какой звукоряд используется:

На сегодняшний день, стандартом звукоряда является "равномерно темперированный строй". В нём, ноты всех аккордов образуются от ноты "ля", а соотношение между соседними нотами всегда одинаковое: 1 делить на корень 12-ой степени из двух.
Значение частоты ноты "ля" в так называемой "первой октаве" (четвёртой по стандарту MIDI) равна 440 герц.
Не мала вероятность того, что вы натыкались на споры о частоте в 432 герца, мол она звучит лучше, что можно услышать от обычных людей, или же что она подсознательно воздействует на организм, лечит любые болезни, и вообще её поменяли, чтобы жили мы хуже, что можно услышать от скрывающихся от властей проповедников правды, которые живут по месту прописки.
А раньше - стандарта на частоту ноты "ля" вообще не было. Её настраивали по-разному для разных композиций и инструментов, что делало каждую мелодию более уникальной. Попробуйте сравнить ноты "ля" в современных мелодиях и на настоящих записях старых композиций: ноты в старых мелодиях зачастую будут звучать намного ниже, ибо частота часто была в районе 415-и герц.
Но просто менять частоту ноты "ля", и образовывать от неё другие - это скучно, ведь это почти равнозначно простому понижению питча итоговой мелодии. Что, если можно добиться очень необычного звучания? Например: поменять звукоряд.
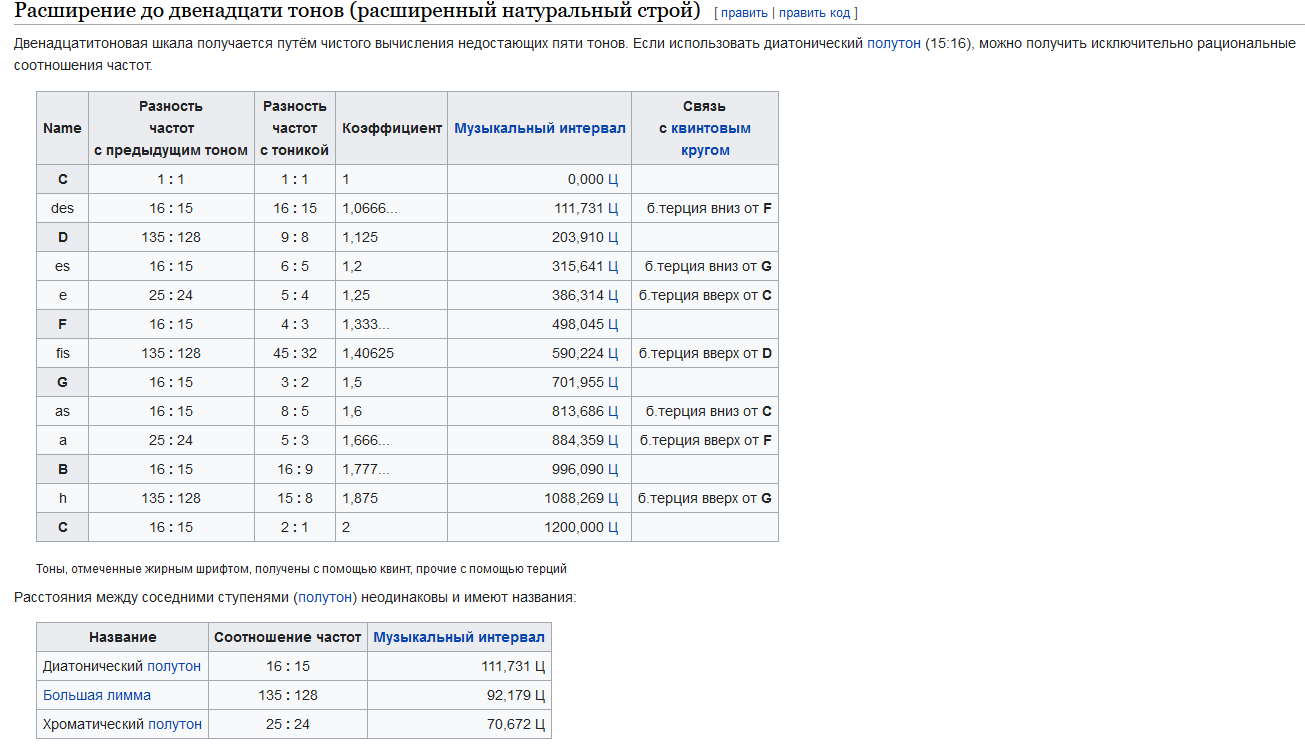
Помимо "равномерно темперированного строя", существует "натуральный строй", в котором аккорды строятся иначе, а соотношение между нотами вообще сумасшедшие, но что главное - они могут быть не равны в разных аккордах, из-за чего вообще все и стали использовать "равномерно темперированный строй". Не уверен, что такое подойдёт для современного композитора, ведь хочется иногда басовую партию прописать сначала на высоких частотах - прописал, сместил вниз, и получил кашу на выходе.
А что, если объединить строи, взяв из "равномерно темперированного строя" тот факт, что все ноты строятся от ноты "ля", а соотношения между нотами взять из "натуральный строя"? Правильно, получится какофония. Возможно, получатся удачные частоты для довольно необычных мелодий.
И так, теперь нужно написать программу, которая вычислит нам все частоты с довольно хорошей точностью, и выдаст их в виде массива дробных чисел.
Для начала нужно понять, какая будет частота ноты "ля" в субконтроктаве (нулевой аккорд по стандарту MIDI):
Стандарт (440) |
440 - 220 - 110 - 55 - 27.5 |
Среднее старых мелодий (415) |
415 - 207.5 - 103.75 - 51.875 - 25.9375 |
Для фанатов 432 (432, ого) |
432 - 216 - 108 - 54 - 27 |
А соотношения можно взять обратные тем, что указаны на картинке немного выше.
Ну, и теперь можно продумать весь алгоритм:
база_ля = 27.5 либо 25.9375 либо 27
колтчество_октав = 15
ноты_равномерные = []
ноты_натуральные = []
// Генерация нот в равномерном соотношении
// Можно заранее высчитать соотношения, ведь они одинаковые
полтона_вверх = 1.0594630943592953
полтона_вниз = 0.9438743126816934
// Основной цикл
для "октава" в количестве "колтчество_октав":
ля = база_ля
умножаем ноту ля на два столько раз, какая сейчас октава - 1
// Теперь считаем ноты, одну за другой
ля_диез = ля * полтона_вверх
си = ля_диез * полтона_вверх
соль_диез = ля * полтона_вниз
соль = соль_диез * полтона_вниз
...
до_диез = ре * полтона_вниз
до = до_диез * полтона_вниз
добавить все ноты в массив друг за другом, от "до" до "си"
// Генерация нот в натуральном соотношении, уже интереснее
для "октава" в количестве "колтчество_октав":
ля = база_ля
умножаем ноту ля на два столько раз, какая сейчас октава - 1
// И начинается самое интересное:
ля_диез = ля * (16/15) иррациональное значение
си = ля_диез * 1.0546875
соль_диез = ля * 0.96
соль = соль_диез * 0.9375
фа_диез = соль * 0.9375
фа = фа_диез * (128/135) иррациональное значение
ми = фа * 0.9375
ре_диез = ми * 0.96
ре = ре_диез * 0.9375
до_диез = ре * (128/135) иррациональное значение
до = до_диез * 0.9375
добавить все ноты в массив друг за другом, от "до" до "си"Как можно заметить, все данные полностью совпадают с официальными, а даже если и не совпадают - то это потому что наш результат более точен, а в официальных данных приведены сокращённые значения.

Реализацию данного алгоритма я уже написал на языке программирования Python, с ней можно ознакомиться в моём репозитории на Codeberg (да здравствует свободное ПО!).
И рассчитав все ноты, получив их в виде массива, можно генерировать звуки нужных частот. Я даже написал программу всё на том же Python, которую можно найти во всё том же репозитории, и которая позволяет сыграть на MIDI клавиатуре мелодию "в любом строю", меняя его нажатием стрелочек "влево" и "вправо".
С частотой ноты "ля" в 415 герц и в "псевдонатуральном строю" ноты звучат словно на полтона ниже, но это не совсем так (что даже можно заметить), и звучат словно более эмоционально, более выразительно и душевно.

А для чего это я делал?
Разумеется, я начал этим увлекаться не просто так. У меня есть наполеоновские планы по созданию собственного, полностью свободного и кросс-платформенного аналога FLStudio, с удобным управлением и красивым дизайном, а не как это сделано в LMMS (без обид, но управление в нём очень кривое, и отвлекает от написания музыки). Я уже даже продумал, как будут устроены инструменты (не VST, но возможно даже лучше, и точно безопаснее, ибо я параноик, и хочу защитить пользователей от уязвимостей через инструменты).
И одной из главных особенностей моего аналога будет передача инструментам не только номера нажатой ноты по стандарту MIDI, но ещё и частоты, чтобы инструменты по большей части работали с частотами, и можно было добиваться необычных звучаний прямо во время написания.
Из проблем пока нерешённость, на чём лучше писать (пока что думаю на C++, с использованием мультимедиа библиотеки SFML), и как генерировать сами звуки, ибо у меня получается пока только шум, но по синусу улетающий в бесконечность. Вторая проблема решится подробным изучением принципов наложения разных волн разных частот для создания красивого звука и принципов работы с сэмплами. Будет сложно, особенно учитывая, что я не варился в музыкальной школе десять лет.
А для тех, кто был в музыкальной школе, и не мало - предлагаю писать в комментарии уточнения для данной статьи, а так же делиться своими необычными фактами. Думаю, многим будет интересно почитать.
А если вы шарите за разработку VST плагинов или вообще заинтересованы в написании свободного аналога FLStudio - можете связаться со мной, можно вместе что-нибудь обдумать.
Премного благодарен за выделенное внимание.
Комментарии (36)

SlavikF
27.11.2022 06:29+16Ссылка на Python script - хорошо, вот только я не знаю, что с ним делать...
Было бы неплохо, если бы автор выложил примеры звучания. Хотя бы просто mp3, или может на Ютуб залить...

iShrimp
27.11.2022 18:33+2Могу предложить такой пример от Gary Garrett: короткая фортепианная мелодия
в темперированном звучании (12edo)
и в натуральном строе
Для обычного "темперированного" слушателя натуральный строй может поначалу звучать расстроенно, звук как бы плывёт, как на старом проигрывателе. Действительно, верхние (мажорные) ряды настроены ниже, чем в 12edo, примерно на 14 центов, а нижние (минорные) - напротив, настроены на 14 центов выше. Потому что натуральная большая терция (5/4) равна не 400, а 386 центам.
Но если послушать и сравнить звучание обеих версий, то можно заметить, как мягче теперь кажется натуральный строй и резче темперированный.

KOCTEP Автор
27.11.2022 19:53Да, лучше послушать чужие реализации, ибо у меня пока что получается только звук по синусоиде, который быстро сведёт с ума даже самого ярого фаната 8-битной музыки

lgorSL
27.11.2022 23:34+1У меня нет музыкального образования, но я пробовал генерировать звук от струны и получалось более-менее интересно.
Колебания струны можно разложить в сумму синусоид. Концы струны закреплены, поэтому возможны колебания, при которых на длину укладывается половина периода, один период, полтора и т.п. На практике будет базовая частота w и гармоники 2w, 3w, 4w...
Разные колебания затухают с разной скоростью - это особенно заметно по гитаре. (Можно предположить, что скорость затухания пропорциональна частоте в какой-то степени, логично попробовать 1 или 2. Начальные амплитуды колебаний на разных частотах можно найти, если представить график "высоты" струны, когда её кто-то потянул вбок, и разложить на сумму синусоид. Я могу ошибаться, но вполне разумным в качестве амплитуд кажется взять гармонический ряд - для w-1, для 2w-1/2, для 3w -1/3 и т.д
На "настоящие" значения влияет место, за которую дёргают струну - середина, 1/3 от длины и т.п., но в целом должно быть что-то похожее.В итоге звук от гитары можно представить как сумму синусоид, затухающих по времени: 1/n sin(wnt) e ^ (-nt)
P.s В жизни всё ещё сложнее, я описал линейную модель.

DmitryKoterov
27.11.2022 22:29+2А нет ли хорошего примера с другой мелодией? Где музыкальная тема прослеживается хотя бы. А то эта кажется какофонией как в одном варианте, так и в другом.

arseniy2
27.11.2022 11:12+2Наверное уже почти в любой DAW можно крутить +-50cents. И будет не от 440, а от другой. И некоторые так делают. Но это ничего не даёт. Ноты дело относительное. Не важно где оно будет стартовать между 415 и 440.
Ну в восточной муз есть хорошие примеры, когда деление не ровно на 12. Но чего-то такого особенного в этом нет.
Кто-то балуется с 19+- нотами в октаве. Опять же, ну и что. Простому человеку, у которого нет времени усиленно развивать музыкальный слух, ничего этого не нужно.
без VST никакого смысла нет. Пока будете пытаться состряпать Serum, Diva, Kontakt, они не только обновятся, а ещё что-нить новое выйдет. Ну а пост-процесс плагины, вряд ли вы состряпаете настолько хорошее, как флагманы. И интерфейсы в DAW на месте не стоят.
P.S.
Забейте на DAW и делайте какой-нить 1 плагин. Хотя бы есть вероятность доделать. Навскидку, нету шибко гибких хорусов пока что.
Компрессоры застряли в схеме 1 статичный трешолд, атака релиз. Хотя можно делать схемки и посложнее, с 2 и более трешолдами(и не статичными), и иметь комбо с вейвшейпером(возможно под капотом у флагманских лимитеров даже что-то такое и есть).
Не видел пока что вейвшейпера с плавно меняющимися кривыми(как аналогия можно представить wavetable). Т.е. плавная смена между большим количеством разных кривых.

whoisking
27.11.2022 11:57+2Компрессоры застряли в схеме 1 статичный трешолд, атака релиз.
Может, я не совсем точно вас понял, но Multiband компрессоры юзаются под десяток лет наверное, в Ableton Live давно есть встроенный, в Bitwig есть dynamics неплохой. В Bitwig вообще можно чудеса творить с недавно вышедшим spectral suite, делая сплит по спектру и на каждый сплит можно навешивать что угодно, тот же компрессор. Да и в целом, во многих DAW давно есть группы, с помощью которых можно разбить сигнал на разные участки и навешивать на них что угодно, мб поэтому люди не видят особого смысла в усложнении компрессоров...

arseniy2
27.11.2022 12:11+1Конечно не правильно. В мультибенде комп работает по той же самой схеме. Просто много тех же самых компов на каждом участке спектра.
речь же про работу трешолд, атак, релиз. которые могут быть не статическими и не единичными. Ну например, один трешолд мог бы ездить вверх вниз реагируя на что-то(например другой трешолд).
Зачем это надо? Такие вещи выявляются только на практике. Также как и применение компов развивалось на практике, а не в уме.
Ну или количество компрессии могло бы влиять на вейвшейпер. Этот вариант даже понятен практически. Например, если вам надо чтобы более низкий уровень сигнала дистортился похоже, как и высокий. Статичным вейвшейпером так не сделать. Рисовать автоматизации долго и муторно.
P.S.
Я заколебался править. Каждый раз при правке в каменте рандомно меняются абзацы! о_О

whoisking
27.11.2022 12:19Не знаю за другие VST, но похоже, что вы можете это сделать в bitwig grid. Его можно юзать и как инструмент и как эффект, вот сейчас смотрю, можно трешхолд привязывать к чему угодно, в базовом случае можно посмотреть пресет Grid compressor.
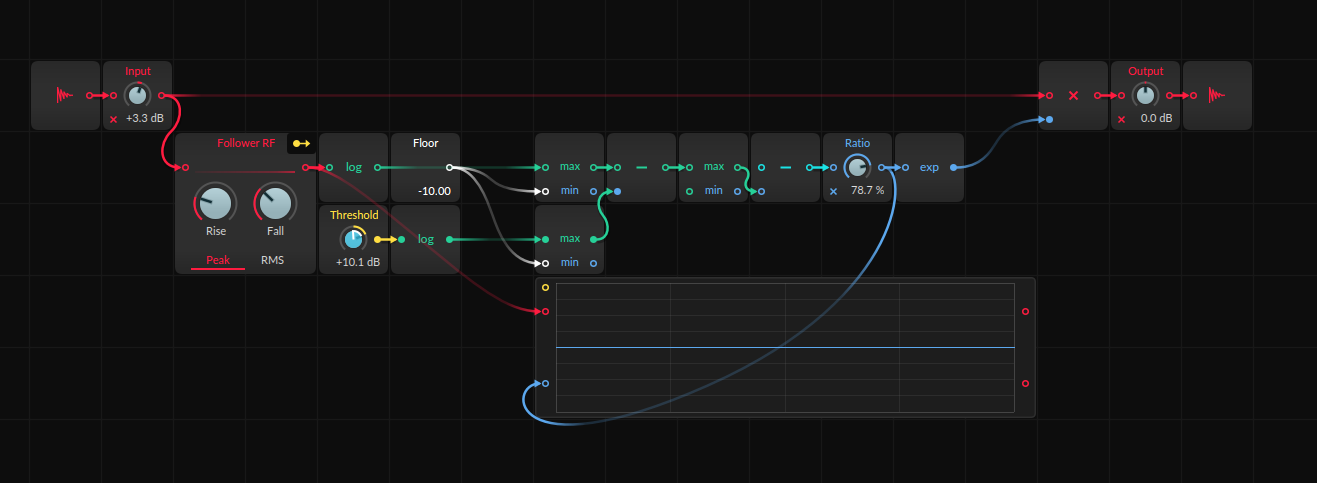
P. S. Похоже, что как раз для таких запросов как ваш и существуют такие штуки как Bitwig Grid, Max for Live =)
arseniy2
27.11.2022 12:25Вполне вероятно. Там накрутить можно очень много чего. Только иметь под рукой готовый, специализированный инструмент тоже хорошо.

SADKO
27.11.2022 18:42Проблема bitwig grid-а и иже с ним, что всё реализуется в лоб, без математической оптимизации и даже понимания необходимости оной, как в примере выше.
Будто это аналоговая схема из идеальных компонентов в которой вы можете сделать сначала тише на 90dB, потом на столько-же громче, и качество звука даже не пострадает ;-) И это ещё самый банальный пример подвоха, которых есть ещё масса куда менее очевидных.
Хорошие приборы, что аналоговые, что цифровые, должны по уму делаться, с глубоким пониманием природы происходящих процессов.

arseniy2
27.11.2022 12:22Я по другому попробую сказать. Комп - это динамический процессор, реагирующий на уровень сигнала. Так чего бы не дать в руки чуть больше инструментов, каким именно образом наш алгоритм будет реагировать на уровень сигнала?

whoisking
27.11.2022 12:33В Fl studio тоже, судя по всему, можно линкать что угодно и по любой формуле

SADKO
27.11.2022 18:29Правильные мысли думаете, но всё придумано дедами ещё до нас, и собиралось из нескольких кубиков. В вашем примере, ничто не мешает сделать посыл на компрессор => шейпер, и накрутить его как лимиттер с временными характеристиками для расстановки акцентов. Тихие и громкие звуки будут единообразно зашейплены.
Динамические уровни и не только, на самом деле делают и давно, просто никто не спешит делиться своими фишками, тем более что музыканты и не требуют, они-же на слух оценивают приборы работать с которыми не умеют. И хорошо продаются те приборы, из которых годный звук может накрутить обезьяна. А какой-то мастеринговый компонент точно делающий то что описано, сам себе звукорежиссёрам не упал.

iShrimp
27.11.2022 17:29+3Существует такой крутой плагин для Reaper под названием Alt-tuner, который позволяет не только перестраивать каждую из 12 степеней октавы, но и создавать собственные звукоряды из любого количества ступеней. Я экспериментировал в нём с перенастройкой классических композиций в натуральный строй. Если кому-то интересно, можете посмотреть другие видео на канале.

pinbraerts
27.11.2022 20:14+1Да, Reaper вполне подходит под понятие условно-бесплатный, спокойно заводится под линуксом. Он напрочь отбивает "наполеоновские" планы по написанию своих студий. Проще написать плагин для рипера на JS, чем свою DAW.

AEP
27.11.2022 17:22+1Давным-давно на Linux Audio Conference был интересный доклад, в котором музыкальная шкала делалась двумерной или даже трехмерной, чтобы от любой ноты можно было точно построить гармонично звучащие рациональные интервалы. https://lac.linuxaudio.org/2014/video.php?id=7

unclegluk
27.11.2022 17:28Жаль, что pyAudio не существует для Андроида. Так не хочется в выходной день садиться за компьютер.

iShrimp
27.11.2022 17:58+2Уважаемый @KOCTEP, всячески поддерживаю ваши начинания и желаю успехов в изучении этой сложной темы. Могу посоветовать ряд информационных ресурсов:
Микротоновая энциклопедия Xenharmonic Wiki: такие статьи, как DAWs и Software (музыкальный софт, поддерживающий кастомные строи), Instruments (акустические инструменты) и Riemann zeta function and tuning (математическое обоснование для поиска идеальных делений октавы, приближающихся к натуральному строю, с помощью Z-функции Римана)
Сайт Tall Kite - теоретика-любителя микротоновой музыки, автора плагина alt-tuner
Руководство к Alt-tuner, которое также является справочником по натуральным и темперированным строям
Сайт Gary Garrett, ещё одного любителя натурального строя, с кучей красивых визуализаций. Пример: песня Flying dream (Youtube).

iShrimp
27.11.2022 18:13+3Для визуализации интервалов и создания клавиатур очень удобно использовать тональную решётку, также известную как Tonnetz, в которой по одной оси отложены квинты (степени числа 3), а по другой - терции (степени числа 5). Октавы здесь не отображаются.
Разные авторы по-разному располагают главные оси на плоскости, но мне кажется естественным, что положительные степени 3 и 5 (обертоны) должны быть направлены вверх и вправо, а отрицательные (унтертоны) - вниз и влево.
Наклонив вертикальную ось под углом 60° и проведя диагонали, получим сетку из треугольников: мажорных - вершиной вверх и минорных - вершиной вниз.
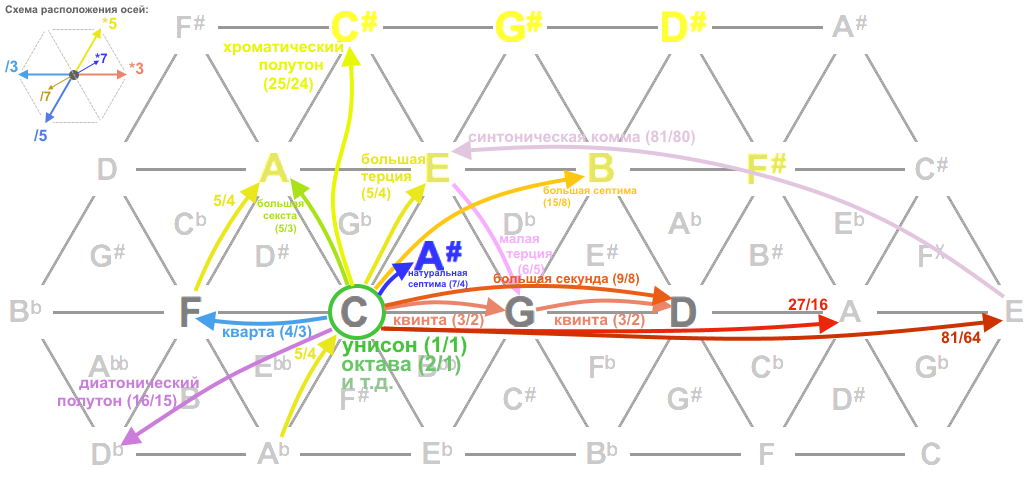
Степени числа 7 можно расположить как бы в третьем измерении, т.е. в вершине тетраэдра, построенного на основе мажорного треугольника.

StjarnornasFred
28.11.2022 03:02+1Ох, дзен-гармония... Я однажды пытался изобрести гамму на не 12 (полу)тонов, а потом понял, что её уже изобрели, рассчитали и сыграли.
Что до натурального строя, то почему-то ни в статье, ни в комментариях не прозвучало самого важного про него. А именно: для человеческого уха наиболее гармоничны те интервалы, где частоты точно соотносятся как небольшие натуральные числа. Например, октава - самый консонирующий интервал - всегда имеет соотношение 2:1. Чистая квинта в натуральном строе - 3:2. Проблема в том, что
нот всего семьто есть двенадцатьчисла в итоге не сходятся. Ведь частоты каждой ноты в натуральном строе берутся как "N квинт - М октав". И тут внезапно всплывает, что произвольно взятая квинта имеет хрен знает какое соотношение и звучит он же знает как (волчья квинта), а значит, инструмент нужно перенастраивать под каждую тональность (ладно, не под каждую, но почти), а в произведении строго избегать нестандартных аккордов. Поэтому плюнули на идеалы и сделали усреднённо-нормальный строй, для которого отклонение от чистых интервалов минимально. Всех устроило, все довольны.
Pavgran
28.11.2022 03:42А именно: для человеческого уха наиболее гармоничны те интервалы, где частоты точно соотносятся как небольшие натуральные числа. Например, октава - самый консонирующий интервал - всегда имеет соотношение 2:1
Это не обязательно так. Автокорреляция и обертоны играют более важную роль.

iShrimp
28.11.2022 18:17Идеальным тембром обладает только идеальная, равномерная, бесконечно тонкая струна. Все реальные звучащие тела, имеющие ненулевую ширину (толщину), слегка (или сильно) негармоничны. Модифицируя тембр, например сделав струну неравномерной толщины, можно заставить диссонировать привычные интервалы (октаву), а вместо них получить новые консонансы, определяемые тембром...

iShrimp
28.11.2022 17:17Да, вы совершенно правы, человеческий слух всюду ищет простые рациональные соотношения. Октава (2,0) и квинта (1,5) - очень сильные созвучия, и они "притягивают" близкие числа в некоторой окрестности. Например, соотношение частот 1,980123 подавляющее большинство людей воспримет скорее как плохо настроенную октаву (это почти 2,00 = 2/1), чем сложную вещь вроде 99/50.
Математическое обоснование этого феномена заключается в том, что одновременно звучащие ноты и их обертона интерферируют и образуют комбинационные тона, в которых мозг угадывает знакомые паттерны. А они, в свою очередь, соответствуют рациональным приближениям звучащего интервала, которые можно получить с помощью его разложения в цепную дробь.
Например: 1,980123 = 1 + 1/1,0202801077... — отбросив дробную часть, получим первое приближение, равное 2;
если раскладывать её дальше, то получим:
1,980123 = 1 + 1 / (1 + 1 / 49,309402829...) — это даёт очередную подходящую дробь 1+1/(1+1/49) = 99/50, и так далее.
Чем ближе очередное дробное число к целому (1,0202... очень близко к 1), тем точнее соответствующее разложение. Поэтому в данном примере в первую очередь будет слышаться октава.
Но проблема в том, что создать инструмент, на котором были бы реализованы все возможные чистые интервалы, физически невозможно. Поэтому была изобретена темперация и равномерные деления октавы.
Для нахождения оптимального РДО можно вывести функцию, показывающую, насколько точно ступени данного РДО аппроксимируют интервалы натурального звукоряда. Причём не обязательно аппроксимировать все натуральные ступени, как сделано в той самой статье о Z-функции Римана. Можно задать лимит простых чисел, которыми будет описываться требуемая гармония, и искать подходящие РДО для 7-лимитной, 11-лимитной и т. д. музыки.


iShrimp
28.11.2022 17:48Для гитары один из лучших звукорядов - 31edo. Он совместим со стандартным гитарным строем EADGBE, он является среднетоновым (в нём нет коммы), и он даёт очень точное и мягкое звучание терций, секст и натуральной септимы. Но квинты и кварты чуть хуже, чем в 12edo.
Также, внезапно пользуются популярностью 22edo-гитары. Это не среднетоновый строй, а скорее суперпифагорейский - с увеличенной квинтой и уменьшенной большой терцией. Комма в нём присутствует, и она растянута до размера 1 ступени, т.е. 1/22 октавы. Между второй (В) и третьей (G) струнами возникает уже не чистая большая терция. Большой тон (9/8) и малый тон (10/9) заметно различаются, и последний звучит довольно "кисло", как какая-нибудь нейтральная секунда (11/10).
Для клавишных инструментов в целях обратной совместимости с 12edo оптимальным выбором будет 72edo. Такой звукоряд имел легендарный советский синтезатор АНС, названный в честь А. Н. Скрябина. Однако, в своё время он редко использовался для сочинения музыки в натуральном строе, в основном на нём создавались различные "инопланетные" звуки и шумовые эффекты для советских фильмов.

ahdenchik
28.11.2022 20:05Ремарка по поводу опенсорсного софта: у нас уже есть JACK, lv2 и Carla - это всё не то?





yea
Фраза не парсится. Наверное, корень двенадцатой степени из двух :)
Mirzapch
Отлично парсится и даже считается. 1.4B79170A07B
KOCTEP Автор
Да, так будет корректнее. Пожалуй, исправлю