В предыдущей статье у нас получился красивый слайдер («карусель») с круговым вращением. А сегодня я создам слайдер, пролистывающий стопку «полароидных» снимков.

Пока не смотрите код, сначала я должен вам многое про него рассказать. Поехали! К старту нашего курса по Fullstack-разработке на Python.

Основные настройки

Большую часть HTML и CSS для этого проекта я возьму из кода кругового слайдера из предыдущей статьи. HTML-разметка абсолютно та же:

<div class="gallery">
  <img src="" alt="">
  <img src="" alt="">
  <img src="" alt="">
  <img src="" alt="">
</div>

А ниже — исходный CSS родительского контейнера .gallery. Контейнер — это грид, где изображения находятся в стопке одно над другим:

.gallery  {
  display: grid;
  width: 220px; /* контроль размера контейнера */
}
.gallery > img {
  grid-area: 1 / 1;
  width: 100%;
  aspect-ratio: 1;
  object-fit: cover;
  border: 10px solid #f2f2f2;
  box-shadow: 0 0 4px #0007;
}

Пока ничего сложного. Для эффекта «полароидности» я использую свойства border и box-shadow. Попробуйте поиграть со стилями, возможно, вам удастся добиться большего! Я же приступлю к самому сложному — к анимации.

В чём фокус?

Логика слайдера основана на порядке размещения изображений в стопке. Да, мы будем работать с z-index. Сначала у всех картинок будет один и тот же z-index, равный 2. Так последнее изображение будет наверху стопки.

Затем последняя картинка смещается вправо, пока не появится следующая. После z-index картинки уменьшается и она помещается обратно в стопку. Теперь её z-index меньше, чем у других изображений, и она перемещается вниз стопки.

Посмотрите на упрощённую демоверсию слайдера. Наведите мышь на изображение, чтобы увидеть анимацию.

Так же нужно поступить с остальными картинками. Вот алгоритм с псевдоселектором :nth-child() для разных изображений:

• Смещаем последнюю картинку (N). Становится видна следующая (N − 1).
• Смещаем следующую картинку (N − 1). Становится видна ещё одна (N − 2).
• Смещаем следующую картинку (N − 2). Становится видна ещё одна (N − 3).
• (Продолжаем, пока не увидим первую картинку)
• Смещаем первое изображение (1) и снова видим последнее (N).

Бесконечный слайдер готов!

Разбираемся с анимацией

В предыдущей статье я написал лишь одну анимацию и проигрывал её с различными задержками для каждого изображения. Здесь будет такой же подход. Для начала давайте представим временную шкалу анимации сначала для трёх картинок, а затем и для любого их числа (N).

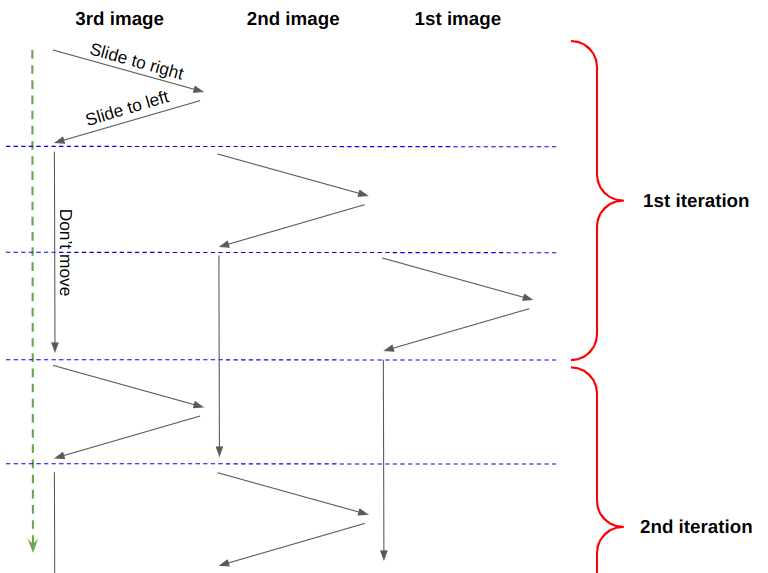
Анимация разбита на три этапа — «смещение вправо», «смещение влево» и «стоп». Задержки между изображениями определяются так: если анимация первой картинки начинается в 0s (0 с), а её продолжительность — 6s (6 с), то анимация второй картинки начинается в -2s (минус 2 с), а третьей — -4s (минус 4 с).

.gallery > img:nth-child(2) { animation-delay: -2s; } /* -1 * 6с / 3 */
.gallery > img:nth-child(3) { animation-delay: -4s; } /* -2 * 6с / 3 */

Также видно, что этап «стоп» занимает две трети времени всей анимации (2*100%/3), а «смещение вправо» и «смещение влево» в сумме занимают треть времени. Следовательно, длительность каждого смещения равна 100%/6 от времени всей анимации.

Ключевые кадры анимации выглядят так:

@keyframes slide {
  0%     { transform: translateX(0%); }
  16.67% { transform: translateX(120%); }
  33.34% { transform: translateX(0%); }
  100%   { transform: translateX(0%); } 
}

120% — произвольная цифра. Нужно значение больше 100%. Изображения должны смещаться вправо за пределы границ других картинок. Необходимо сместить изображения по крайней мере на 100% от их размера. Вот почему я выбрал число 120% — чтобы получить немного дополнительного места.

Далее нужно прописать значения z-index. Помните, что необходимо обновлять z-indexкартинки после того, как она сместится вправо.

@keyframes slide {
  0%     { transform: translateX(0%);   z-index: 2; }
  16.66% { transform: translateX(120%); z-index: 2; }
  16.67% { transform: translateX(120%); z-index: 1; } /* здесь обновляем порядок наложения по оси z */
  33.34% { transform: translateX(0%);   z-index: 1; }
  100%   { transform: translateX(0% );  z-index: 1; }  
}

Вместо того чтобы определить одно состояние на точке временной линии, равной 16.67% (100%/6), определим два состояния почти в одной и той же точке (16.66 и 16.67%), где z-index уменьшается перед тем, как изображение смещается обратно в стопку.

Вот что произойдёт после того, как мы соединим всё вместе.

Странно, смещение работает нормально, но порядок изображений в стопке неправильный. Анимация начинается правильно, верхнее изображение перемещается назад… Но следующие изображения не следуют этому примеру. Обратите внимание на вторую картинку — она возвращается на верх стопки, а затем следующее фото появляется поверх неё.

Давайте внимательно посмотрим на изменения z-index. Изначально у всех изображений z-index равен 2. Это значит, что порядок картинок в стопке выглядит так…

Наш взгляд ???? --> третье фото (2) | второе фото (2) | первое фото (2)

Третья картинка смещается, её z-index обновляется. Теперь порядок картинок таков:

Наш взгляд ???? --> второе фото (2) | первое фото (2) | третье фото (1)

То же самое делаем со второй картинкой:

Наш взгляд ???? --> первое фото (2) | третье фото (1) | второе фото (1)

…и с первой:

Наш взгляд ???? --> третье фото (1) | второе фото (1) | первое фото (1)

Вроде бы всё должно быть в порядке, но на самом деле нет! Когда первая картинка перемещается назад, третья начинает новую итерацию, что означает, что её z-index снова становится равным 2:

Наш взгляд ???? --> третье фото (2) | второе фото (1) | первое фото (1)

На самом деле все изображения никогда не получали значение z-index, равное 2! Когда изображения неподвижны (к примеру, на этапе «стоп»), z-index равен 1. Если третье фото смещается, а его z-index изменяется с 2 до 1, оно остается поверх стопки! Если у всех изображений одинаковый `z-index, последнее в исходной последовательности — в данном случае третье — оказывается сверху. Смещение третьего изображения приводит к следующему:

Наш взгляд ???? --> третье фото (1) | второе фото (1) | первое фото (1)

Третье изображение всё ещё поверх стопки, а следом наверх перемещается второе, когда его анимация перезапускается при z-index: 2:

Наш взгляд ???? --> второе фото (2) | третье фото (1) | первое фото (1)

Когда оно смещается, получается вот что:

Наш взгляд ???? --> третье фото (1) | второе фото (1) | первое фото (1)

А затем сверху оказывается первая картинка:

Наш взгляд ???? --> первое фото (2) | третье фото (1) | второе фото (1)

Я запутался. Получается, что вся логика неверна?

Знаю, это сложно. Но наша логика отчасти правильна. Нужно немного изменить анимацию, и всё заработает. Фокус в том, чтобы верно сбросить значение z-index.

Давайте вернёмся на этап, когда третье изображение находилось сверху стопки:

Наш взгляд ???? --> третье фото (2) | второе фото (1) | первое фото (1)

После смещения третьей картинки и изменения её z-indexона остаётся сверху. Нам же необходимо обновить z-index второй картинки. Давайте перед смещением третьего изображения за пределы стопки сделаем z-index второго изображения равным 2.

Другими словами, z-index второй картинки сбрасывается перед окончанием анимации.

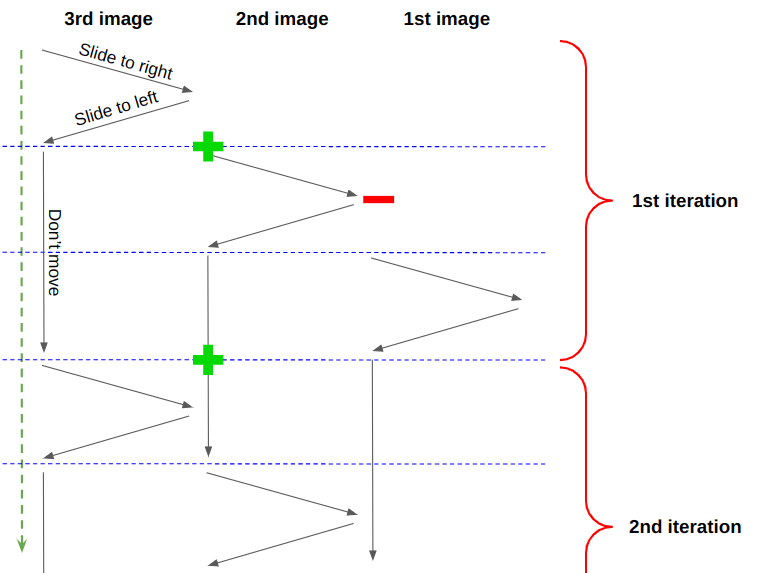
Зелёный плюс означает увеличение z-index до 2, а красный минус — уменьшение до 1. Второе фото сначала имеет z-index, равный 2, а при смещении из стопки он уменьшается до 1. Но, прежде чем первое изображение смещается из стопки, сделаем z-index второго изображения равным 2. Таким образом, z-index первого и z-index второго изображения получаются одинаковыми. Но третье изображение всё равно окажется сверху, так как в DOM оно появляется позже. После смещения третьего фото и обновления его z-indexоно оказывается внизу стопки.

Это происходит на двух третях анимации. Необходимо соответствующим образом обновить ключевые кадры:

@keyframes slide {
  0%     { transform: translateX(0%);   z-index: 2; }
  16.66% { transform: translateX(120%); z-index: 2; }
  16.67% { transform: translateX(120%); z-index: 1; } /* здесь обновляем порядок наложения по оси z... */
  33.34% { transform: translateX(0%);   z-index: 1; }
  66.33% { transform: translateX(0%);   z-index: 1; }
  66.34% { transform: translateX(0%);   z-index: 2; } /* ...а также здесь */
  100%   { transform: translateX(0%);   z-index: 2; }  
}

Уже лучше, но все ещё не совсем…

Это никогда не кончится

Не беспокойтесь, нам не придётся снова менять ключевые кадры, ведь такая ситуация возникает, только если в анимации задействовано последнее фото. Можно создать «особую» анимацию ключевых кадров специально для решения проблемы последнего изображения.

Когда первое фото находится сверху, происходит следующее:

Наш взгляд ???? -->  первое фото (2) | третье фото (1) | второе фото (1)

После предыдущего изменения третье изображение появится сверху перед смещением первого. Так происходит только сейчас, потому что следующее изображение, которое двигается после первого, — это последнее изображение, которое находится выше в DOM. Остальные фото работают, как нужно, потому что сначала идёт N, затем — N - 1, потом 3 меняется на 2, а 2 на 1… Но затем происходит переход от 1 к N.

Избежим этого, используя следующие ключевые кадры для последнего изображения:

@keyframes slide-last {
  0%     { transform: translateX(0%);   z-index: 2;}
  16.66% { transform: translateX(120%); z-index: 2; }
  16.67% { transform: translateX(120%); z-index: 1; } /* здесь обновляем порядок наложения по оси z... */
  33.34% { transform: translateX(0%);   z-index: 1; }
  83.33% { transform: translateX(0%);   z-index: 1; }
  83.34% { transform: translateX(0%);   z-index: 2; } /* ...а также здесь */
  100%   { transform: translateX(0%);   z-index: 2; }
}

z-index сбрасывается на 5/6 анимации (а не на 2/3), когда первое фото находится вне стопки. Больше никакого выпрыгивания картинки!

Ура. Теперь всё работает безупречно! Вот окончательный код во всём его великолепии:

.gallery > img {
  animation: slide 6s infinite;
}
.gallery > img:last-child {
  animation-name: slide-last;
}
.gallery > img:nth-child(2) { animation-delay: -2s; } 
.gallery > img:nth-child(3) { animation-delay: -4s; }

@keyframes slide {
  0% { transform: translateX(0%); z-index: 2; }
  16.66% { transform: translateX(120%); z-index: 2; }
  16.67% { transform: translateX(120%); z-index: 1; } 
  33.34% { transform: translateX(0%); z-index: 1; }
  66.33% { transform: translateX(0%); z-index: 1; }
  66.34% { transform: translateX(0%); z-index: 2; } 
  100% { transform: translateX(0%); z-index: 2; }
}
@keyframes slide-last {
  0% { transform: translateX(0%); z-index: 2; }
  16.66% { transform: translateX(120%); z-index: 2; }
  16.67% { transform: translateX(120%); z-index: 1; }
  33.34% { transform: translateX(0%); z-index: 1; }
  83.33% { transform: translateX(0%); z-index: 1; }
  83.34% { transform: translateX(0%); z-index: 2; } 
  100%  { transform: translateX(0%); z-index: 2; }
}

Поддержка любого числа изображений

Теперь, когда анимация правильно отображает три фотографии, давайте перепишем код так, чтобы он работал с любым числом (N) картинок. Но сначала оптимизируем и уберём избыточный код. Для этого разделяем анимацию:

.gallery > img {
  z-index: 2;
  animation: 
    slide 6s infinite,
    z-order 6s infinite steps(1);
}
.gallery > img:last-child {
  animation-name: slide, z-order-last;
}
.gallery > img:nth-child(2) { animation-delay: -2s; } 
.gallery > img:nth-child(3) { animation-delay: -4s; }

@keyframes slide {
  16.67% { transform: translateX(120%); }
  33.33% { transform: translateX(0%); }
}
@keyframes z-order {
  16.67%,
  33.33% { z-index: 1; }
  66.33% { z-index: 2; }
}
@keyframes z-order-last {
  16.67%,
  33.33% { z-index: 1; }
  83.33% { z-index: 2; }
}

Теперь кода намного меньше! Я создал отдельную анимацию для смещения, а другую — для обновления z-index. Обратите внимание, что при анимации z-index используется steps(1). Я использую steps(1), потому что хочу резко изменить значение z-index, а не постепенно, как в анимации сдвига.

Теперь код легче читать и поддерживать. Стало ясно, как работать с любым числом изображений. Необходимо обновлять задержки анимации и процентные значения ключевых кадров. С задержками всё просто — можно использовать цикл, который я написал в предыдущей статье для поддержки множества изображений в круговом слайдере:

@for $i from 2 to ($n + 1) {
  .gallery > img:nth-child(#{$i}) {
    animation-delay: calc(#{(1 — $i)/$n}*6s);
  }
}

От ванильного CSS переходим к SASS. Затем представим, как временная шкала изменяется при наличии N количества изображений. Не стоит забывать, что анимация состоит из трёх этапов:

После «смещения вправо» и «смещения влево» изображение должно оставаться неподвижным, пока другие картинки не пройдут через анимации. Так что этап «стоп» должен длиться столько же, сколько и этапы (N − 1) «смещения вправо» и «смещения влево». В течение одной итерации «сместятся» N изображений. Таким образом, «смещение вправо» и «смещение влево» вместе длятся 100%/N от общего времени анимации. Изображение выходит из стопки в (100%/N)/2 и входит обратно в стопку в 100%/N.

Этот код:

@keyframes slide {
  16.67% { transform: translateX(120%); }
  33.33% { transform: translateX(0%); }
}

заменяем на этот:

@keyframes slide {
  #{50/$n}%  { transform: translateX(120%); }
  #{100/$n}% { transform: translateX(0%); }
}

Если заменить N на 3, получается 16.67 и 33.33%, если в стопке три фотографии. Применяя такую же логику для порядка наложения, получаем следующее:

@keyframes z-order {
  #{50/$n}%,
  #{100/$n}% { z-index: 1; }
  66.33% { z-index: 2; }
}

Нам всё ещё нужно обновить значение 66.33%. В этой точке сбрасывается z-index изображения перед окончанием анимации и одновременно следующее изображение начинает смещаться. Смещение занимает 100%/N, а сброс z-index происходит в 100% — 100%/N:

@keyframes z-order {
  #{50/$n}%,
  #{100/$n}% { z-index: 1; }
  #{100 — 100/$n}% { z-index: 2; }
}

Но для работы анимации z-order-last сброс z-index должен произойти чуть позже. Помните о фиксе для последней фотографии? Сброс z-index должен происходить, когда первая картинка находится вне стопки, а не когда она начинает смещение. Здесь используется схожий подход:

@keyframes z-order-last {
  #{50/$n}%,
  #{100/$n}% { z-index: 1; }
  #{100 — 50/$n}% { z-index: 2; }
}

Готово! Вот слайдер с пятью картинками:

Для красоты добавим поворот:

Я всего лишь добавил rotate(var(--r)) к свойству transform. В цикле --r — случайный угол:

@for $i from 1 to ($n + 1) {
  .gallery > img:nth-child(#{$i}) {
    --r: #{(-20 + random(40))*1deg}; /* случайный угол между -20 и 20 градусами */
  }
}

Поворот приводит к возникновению небольших глитчей. Иногда изображения перепрыгивают в конец стопки, но это не важно.

Заключение

Вся работа с z-index потребовала точной настройки. Если раньше вы не были уверены, как работает порядок наложения, то теперь, надеюсь, вы понимаете принцип его работы гораздо лучше! Если вам что-то показалось непонятным, настоятельно советую вам ещё раз прочитать эту статью и расписать всё на бумаге. Попробуйте проиллюстрировать каждый шаг анимации, используя разное количество изображений, чтобы лучше понять, как всё работает.

В прошлой статье я показал несколько геометрических хитростей и создал закольцованный круговой слайдер. Сегодня — сделал что-то похожее с помощью z-index. В обоих случаях я не дублировал картинки для создания непрерывной анимации и не использовал JavaScript.

А в следующей статье я покажу вам, как создать трёхмерный слайдер. Не переключайтесь!

• Профессия Fullstack-разработчик на Python (16 месяцев)
• Профессия Data Scientist (24 месяца)