Фракталы — это бесконечные сложные узоры, которые самоподобны в разных масштабах. Например, ствол дерева расщепляется на ветки. Те распадаются на еще более мелкие ветви и так далее. Программная генерация фракталов превратит простые формы в сложные узоры. Я покажу, как построить впечатляющие фракталы при помощи Python простой геометрии и знания программирования.
Фракталы важны и в науке о данных. Например, фрактальный анализ оценивает фрактальные характеристики наборов данных, чтобы помочь понять структуру процессов в основе данных. А рекуррентный алгоритм — центр генерации фракталов — может применяться к широкому кругу задач с данными, от алгоритма двоичного поиска до рекуррентных нейронных сетей.
Идея
Я хочу написать программу, которая рисует равносторонний треугольник. Затем на каждой стороне треугольника эта же программа рисует треугольник поменьше, обращенный наружу. Должна быть возможность повторять рисование столько раз, сколько нужно, чтобы отрисовать интересные узоры.

Этот набросок — тип узора, который хочется нарисовать
Представление изображения
Изображение я представлю как двумерный массив пикселей. Каждая ячейка в массиве пикселей — это цвет пикселя в RGB. Библиотекой NumPy воспользуемся для генерации массива пикселей, а Pillow — для превращения массива в изображение, которое можно сохранить.

Синий пиксель имеет значение x равное 3, а y — 4, а значит, доступ к нему можно получить строкой pixels[4][3].
Рисуем линию
Нам нужна функция, которая принимает две координаты и между ними рисует линию.
Приведенный ниже код работает путем интерполяции между двумя точками, с каждым шагом добавляя в массив новые пиксели. Это как раскрашивание линии пиксель за пикселем.
import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
# Figure out the boundaries of our pixel array
max_x_coordinate = len(pixels[0])
max_y_coordinate = len(pixels)
# The distances along the x and y axis between the 2 points
horizontal_distance = to_coordinates[1] - from_coordinates[1]
vertical_distance = to_coordinates[0] - from_coordinates[0]
# The total distance between the two points
distance = math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
+ (to_coordinates[0] - from_coordinates[0])**2)
# How far we will step forwards each time we colour in a new pixel
horizontal_step = horizontal_distance/distance
vertical_step = vertical_distance/distance
# At this point, we enter the loop to draw the line in our pixel array
# Each iteration of the loop will add a new point along our line
for i in range(round(distance)):
# These 2 coordinates are the ones at the center of our line
current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
# Once we have the coordinates of our point,
# we draw around the coordinates of size 'thickness'
for x in range (-thickness, thickness):
for y in range (-thickness, thickness):
x_value = current_x_coordinate + x
y_value = current_y_coordinate + y
if (x_value > 0 and x_value < max_x_coordinate and \
y_value > 0 and y_value < max_y_coordinate):
pixels[y_value][x_value] = colour
# Define the size of our image
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# Draw a line
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# Turn our pixel array into a real picture
img = Image.fromarray(pixels)
# Show our picture, and save it
img.show()
img.save('Line.png')
Я попросил функцию нарисовать желтую линию по углам массива пикселей
Треугольник
Теперь у нас есть функция, которая проводит линию между двумя точками. Нарисуем первый равносторонний треугольник.
Взяв центральную точку и длину стороны треугольника, с помощью удобной формулы вычислим высоту: h = ½(√3a).
Теперь, используя эту высоту, центральную точку и длину стороны, я могу определить, где должен находиться каждый угол треугольника. А функция plot_line проведет линию между углами.
def draw_triangle(center, side_length, thickness, colour, pixels):
# The height of an equilateral triangle is, h = ½(√3a)
# where 'a' is the side length
triangle_height = round(side_length * math.sqrt(3)/2)
# The top corner
top = [center[0] - triangle_height/2, center[1]]
# Bottom left corner
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# Bottom right corner
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
# Draw a line between each corner to complete the triangle
plot_line(top, bottom_left, thickness, colour, pixels)
plot_line(top, bottom_right, thickness, colour, pixels)
plot_line(bottom_left, bottom_right, thickness, colour, pixels)
Генерация фрактала
Последний шаг, пожалуй, самый сложный. Я хочу, чтобы функция треугольника вызывала сама себя для каждой стороны треугольника. Для этого нужно вычислять центральную точку каждого из новых меньших треугольников и правильно поворачивать их, так, чтобы они были направлены перпендикулярно стороне, к которой прикреплены.
Мы можем использовать эту функцию для поворота каждого угла треугольника, вычитая смещение центральной точки из координат, которые я хочу повернуть, а затем применяя формулу для поворота пары координат.
def rotate(coordinate, center_point, degrees):
# Subtract the point we are rotating around from our coordinate
x = (coordinate[0] - center_point[0])
y = (coordinate[1] - center_point[1])
# Python's cos and sin functions take radians instead of degrees
radians = math.radians(degrees)
# Calculate our rotated points
new_x = (x * math.cos(radians)) - (y * math.sin(radians))
new_y = (y * math.cos(radians)) + (x * math.sin(radians))
# Add back our offset we subtracted at the beginning to our rotated points
return [new_x + center_point[0], new_y + center_point[1]]
Треугольник, в котором каждую координату мы повернули на 35 градусов
Теперь, когда я могу вращать треугольник, переключу внимание на рисование меньших треугольников.
Для этого я дописал draw_triangle так, чтобы для каждого ребра вычислить поворот и центральную точку нового треугольника с длиной стороны, уменьшенной на параметр shrink_side_by.
После вычисления центральной точки и поворота нового треугольника функция вызывает draw_triangle (саму себя), чтобы из центра текущей линии нарисовать новый треугольник меньше. Так один блок кода вычислит другой набор центральных точек и вращений меньшего треугольника.
Такой алгоритм называется рекурсивным: функция draw_triangle будет вызывать себя, пока не достигнет количества треугольников max_depth. Это условие важно потому, что иначе произойдет ошибка переполнения стека.
def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \
pixels, shrink_side_by, iteration, max_depth):
# The height of an equilateral triangle is, h = ½(√3a)
# where 'a' is the side length
triangle_height = side_length * math.sqrt(3)/2
# The top corner
top = [center[0] - triangle_height/2, center[1]]
# Bottom left corner
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# Bottom right corner
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
if (degrees_rotate != 0):
top = rotate(top, center, degrees_rotate)
bottom_left = rotate(bottom_left, center, degrees_rotate)
bottom_right = rotate(bottom_right, center, degrees_rotate)
# Coordinates between each edge of the triangle
lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]]
line_number = 0
# Draw a line between each corner to complete the triangle
for line in lines:
line_number += 1
plot_line(line[0], line[1], thickness, colour, pixels)
# If we haven't reached max_depth, draw some new triangles
if (iteration < max_depth and (iteration < 1 or line_number < 3)):
gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1])
new_side_length = side_length*shrink_side_by
# Center of the line of the traingle we are drawing
center_of_line = [(line[0][0] + line[1][0]) / 2, \
(line[0][1] + line[1][1]) / 2]
new_center = []
new_rotation = degrees_rotate
# Amount we need to rotate the traingle by
if (line_number == 1):
new_rotation += 60
elif (line_number == 2):
new_rotation -= 60
else:
new_rotation += 180
# In an ideal world this would be gradient == 0,
# but due to floating point division we cannot
# ensure that this will always be the case
if (gradient < 0.0001 and gradient > -0.0001):
if (center_of_line[0] - center[0] > 0):
new_center = [center_of_line[0] + triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
new_center = [center_of_line[0] - triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
# Calculate the normal to the gradient of the line
difference_from_center = -1/gradient
# Calculate the distance from the center of the line
# to the center of our new traingle
distance_from_center = triangle_height * (shrink_side_by/2)
# Calculate the length in the x direction,
# from the center of our line to the center of our new triangle
x_length = math.sqrt((distance_from_center**2)/ \
(1 + difference_from_center**2))
# Figure out which way around the x direction needs to go
if (center_of_line[1] < center[1] and x_length > 0):
x_length *= -1
# Now calculate the length in the y direction
y_length = x_length * difference_from_center
# Offset the center of the line with our new x and y values
new_center = [center_of_line[0] + y_length, \
center_of_line[1] + x_length]
draw_triangle(new_center, new_side_length, new_rotation, \
thickness, colour, pixels, shrink_side_by, \
iteration+1, max_depth)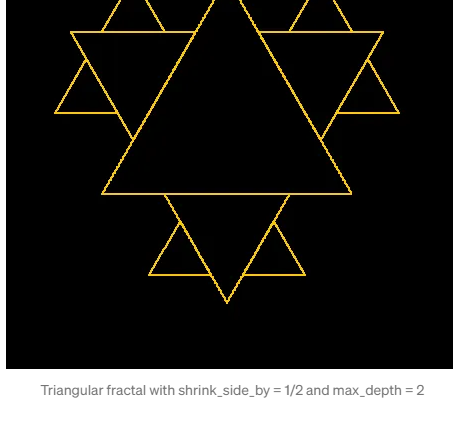
Фрактал с параметрами shrink_side_by = 1/2 и max_depth = 2
Результаты
Ниже приведены примеры изображений, которые мы можем сгенерировать, изменив значения параметров shrink_side_by и max_depth в draw_triangle.
Интересно, что эти крупные повторяющиеся узоры часто порождают формы сложнее, например завораживающе симметричные шестиугольники.

В симметрии повторяющихся треугольников начинают проявляться все более сложные формы.
 Фрактал-снежинка при помощи версии
Фрактал-снежинка при помощи версии draw_triangle, которая рисует треугольники сторонами внутрь

Другое творение с небольшим уменьшением в размерах на каждой итерации
Заключение
Творческий подход поможет создавать впечатляющие структуры.
Разобравшись с основными свойствами фракталов и применив рекурсивный алгоритм, мы создали прочную основу, которая также поможет разобраться со сложными задачами науки о данных.
Загружайте и читайте код здесь. Если знаете, как сделать код лучше, свяжитесь со мной.
Data Science и Machine Learning
- Профессия Data Scientist
- Профессия Data Analyst
- Курс «Математика для Data Science»
- Курс «Математика и Machine Learning для Data Science»
- Курс по Data Engineering
- Курс «Machine Learning и Deep Learning»
- Курс по Machine Learning
Python, веб-разработка
- Профессия Fullstack-разработчик на Python
- Курс «Python для веб-разработки»
- Профессия Frontend-разработчик
- Профессия Веб-разработчик
Мобильная разработка
Java и C#
- Профессия Java-разработчик
- Профессия QA-инженер на JAVA
- Профессия C#-разработчик
- Профессия Разработчик игр на Unity
От основ — в глубину
А также



matveypol003
Можешь пожалуйста расставить отступы в коде?