Если вы занимаетесь обучением крупных современных нейросетей, эта статья будет вам не совсем в тему, ведь у A100 скорость в сто раз выше (156 терафлопсов).

Так что же интересного в этих полутора терафлопсах?

• работа на одном ядре MacBook Air 2020 года с питанием от батареи;
• выполнение с задержкой ~0,5 наносекунды на инструкцию.

Мы говорим не о мощных ускорителях или тензорных ядрах графических процессоров, а лишь о настоящей производительности линейной алгебры, которая отстоит от регистров процессора на один цикл.

Как ни странно, Apple прячет от нас эту штуку! Но в этой статье мы рассмотрим код, который позволит нам приподнять завесу тайны. Для всего кода используется заголовок aarch.h в замечательном репозитории corsix.

Что такое сопроцессор AMX?

По сути, это SIMD на стероидах. Важная особенность в том, что отношение AMX:CPU не равно 1:1. Сопроцессор AMX есть не у каждого ядра.

Вот размеры, которые можно использовать для загрузки или хранения значений:

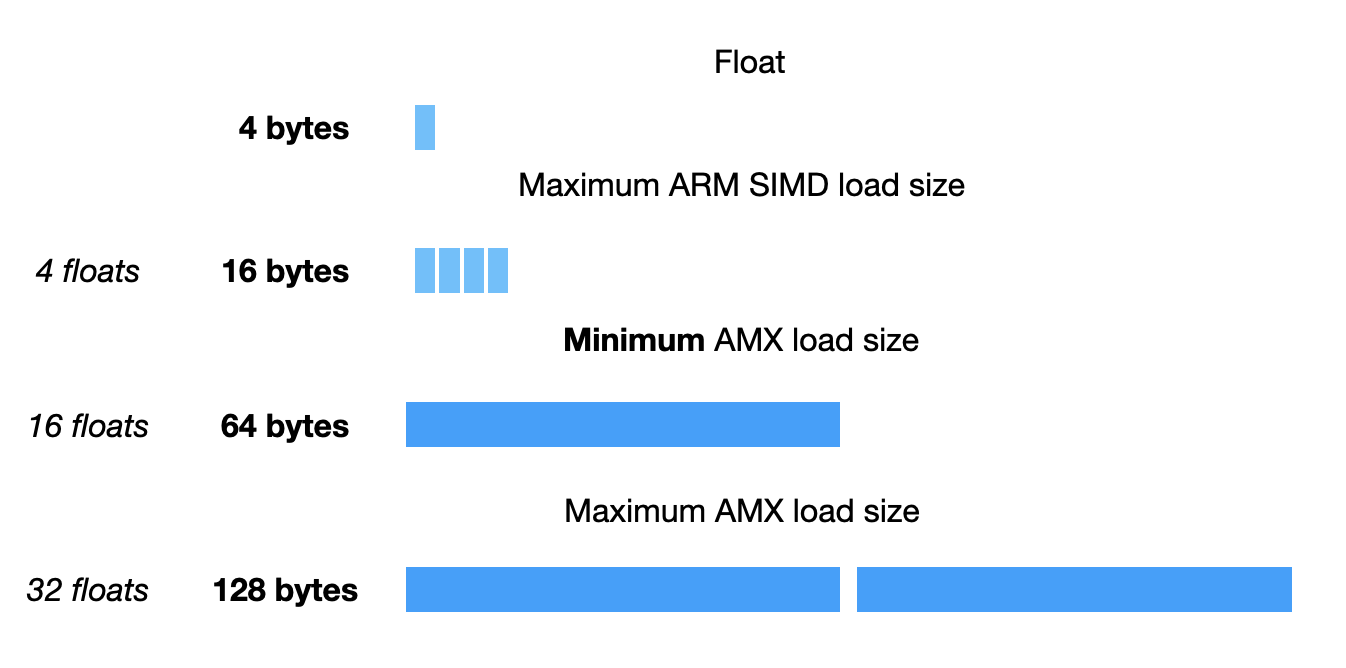
Размер minimum равен ширине полного регистра AVX512.

Но откуда загружаются или где хранятся эти значения? Понятно, что такие размеры довольно быстро заполнили бы файл регистра NEON. Есть отдельный регистровый файл специально для AMX, выглядит он весьма странно.

Регистры распределены по группам X, Y и Z. В группах X и Y хранятся входные значения для каждой инструкции, а в группе Z — выходные значения.

Группы X и Y уже не маленькие! На них ушел целый килобайт. Ну а Z вообще ни в какие ворота:

Спойлер: 1024 байт (1/4 от группы Z-регистров) могут быть полностью заняты одной инструкцией AMX.

И как же попасть из X и Y в Z? Способов так много, что все они едва ли уместятся в кодировку ISA, поэтому большую часть информации об инструкциях Apple закодировали в регистре общего назначения. Оказалось, что с этим классно работать, ведь есть возможность конфигурировать код на AMX на лету, во время его выполнения.

Цель этого поста — добиться от сопроцессора предельной мощности. Есть инструкции умножения векторов, которые выводят векторы одинаковой длины, но они далеко не исчерпывают вычислительные возможности этой микросхемы. Чтобы добиться реального эффекта, придется вместо этого использовать внешнее произведение.

Что такое внешнее произведение? Пусть есть два вектора u и v? тогда:

Внешнее произведение этих векторов — это матрица, которая содержит произведения всех возможных попарных комбинаций их элементов. Это немного проясняет, почему группа регистров Z настолько больше групп X и Y.

В микросхеме AMX это сводится к очень простой, вот такой инструкции:

Ещё есть флаг, который можно установить, чтобы суммировать с нарастанием (accumulate) данные из прошлого результата:

Итак, у нас есть все необходимое, чтобы написать умножение матриц: перезагрузим 16 значений с плавающими точками из входных матриц и суммируем их внешние произведения с нарастанием в выводе размерностью 16x16. При этом уменьшение размерности K никакой роли не играет!

Упростим задачу и неявно транспонируем матричное умножение. Как A, так и B (наши входные данные) как основную размерность будут иметь размерность уменьшения K. На практике это не имеет большого значения, но значительно упрощает код.

Вот ссылка, при помощи которой предложенное решение можно проверить:

void reference_16x16xK(float *A, float *B, float *C, uint64_t K) {
  for (uint32_t m = 0; m < 16; ++m) {
    for (uint32_t n = 0; n < 16; ++n) {
      C[n * 16 + m] = 0;
      for (uint32_t k = 0; k < K; ++k) {
        C[n * 16 + m] += A[k * 16 + m] * B[k * 16 + n];
      }
    }
  }
}

А вот как проверить его на AMX:

// only set for k == 0
uint64_t reset_z = 1ull << 27;

for (uint32_t k = 0; k < K; ++k) {
  uint64_t idx = k % 4;
  // 64 bytes = 16 floats
  AMX_LDX((uint64_t)A + k * 64);
  AMX_LDY((uint64_t)B + k * 64);

  // now we do 4 indepedent outer products (avoiding pipeline hazards)
  AMX_FMA32(reset_z);
  reset_z = 0;
}

Примечательно, что мы не обращались по адресу ни к одному регистру. Вернее, обращались, но тайно. Точно так же, как reset_z кодируется битовой маской, адреса регистров кодируются в аргументах, передаваемых AMX_*. Указатели на A и B используют лишь до 56 бит, поэтому инженеры Apple запрятали данные в оставшихся восьми битах. Мы просто случайно установили их все в значение 0. Итак, в данном случае применяются регистры "0" для X и Y.

Код для сохранения регистров Z в памяти немного сложнее: заполняется только первый столбец. Это означает, что нужно занять регистры 0, 4, 8 и т. д.:

for (uint64_t i = 0; i < 16; ++i) {
  const uint64_t z_register = (i * 4ull) << 56;
  AMX_STZ(z_register | (uint64_t)C + i * 64);
}

К сожалению, если загрузить размещенный выше код, мы увидим, что он страшно тормозит. А ведь это всего какая-то пара сотен гигафлопов. Почему же? Есть две причины.

Первая — конфликт при конвейерной обработке (pipeline hazard)

pipeline hazard — общее название случаев, когда результаты одной инструкции требуются для выполнения последующей до того, как первая завершится.

Каждая инструкция AMX_FMA32 зависит от предыдущей, поскольку мы суммируем с нарастанием в единое подмножество регистрового файла. В итоге используется 25% регистрового файла на полную мощность, а остальное мы оставляем незадействованным, что мешает распараллеливанию на уровне инструкций.

Вторая причина — неэффективная загрузка из памяти. Одновременно можно загружать 128 байт, но приведенный выше код загружает всего 64 байта. Аналогично мы можем выполнять загрузку в другие регистры, а не загружать каждый раз в одни и те же. Это тоже позволяет немного распараллелиться на уровне инструкций.

И какой же у нас план?

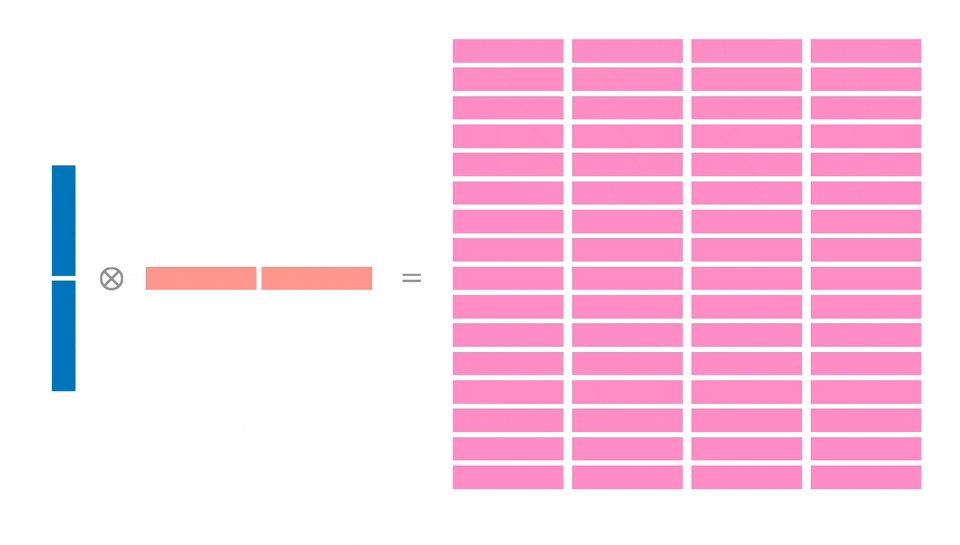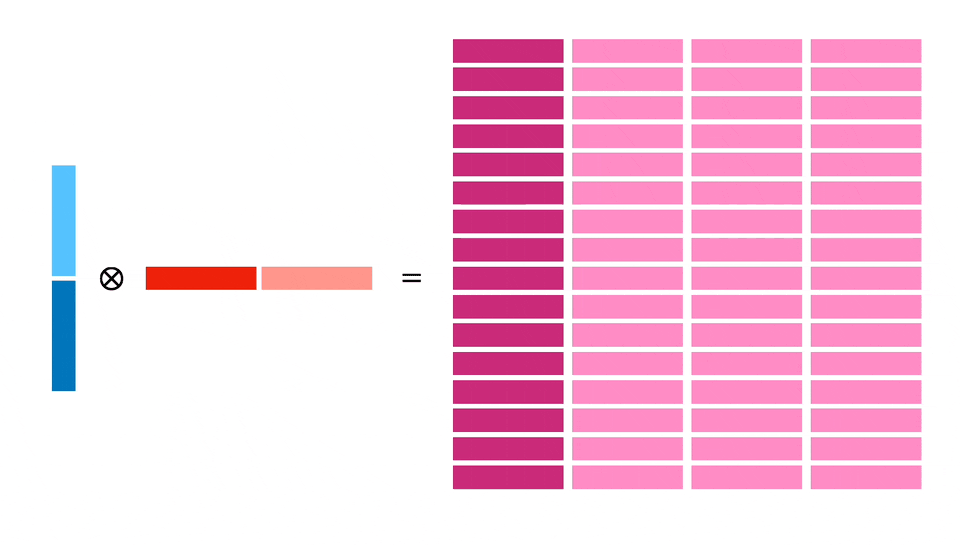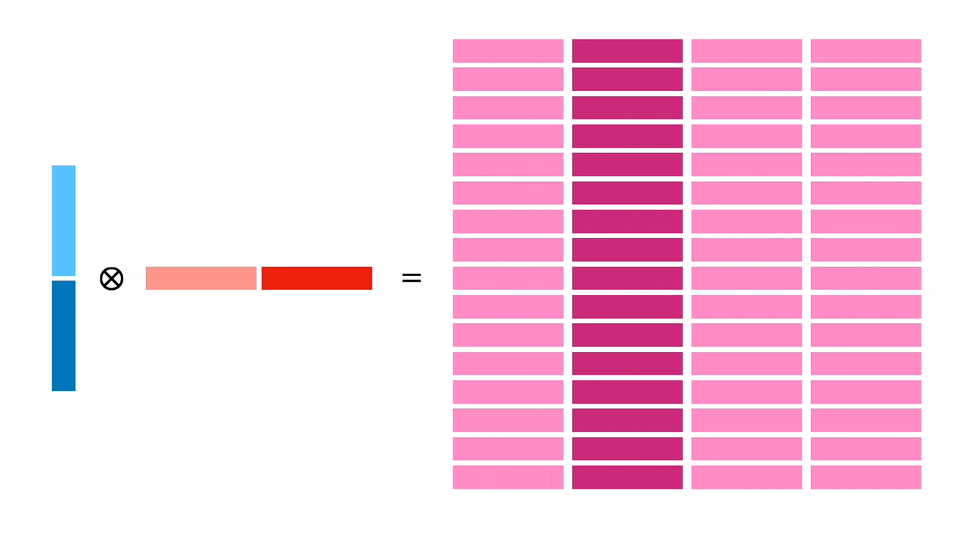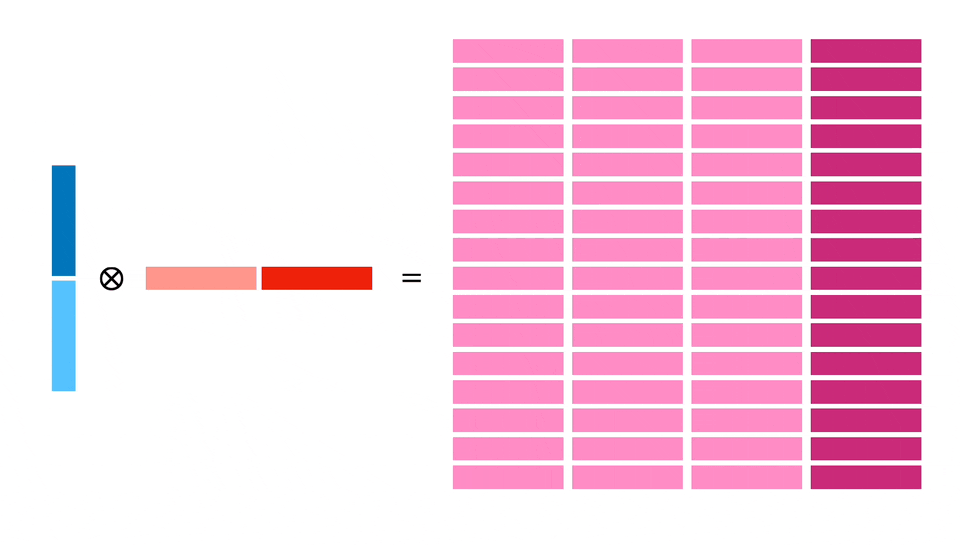
Мы планируем загрузить 128 байт в X и Y и затем рассчитать блок 32x32. Для этого потребуется 4 независимых расчета блоков по 16x16, что позволит добиться параллелизма на уровне инструкций, а также более эффективно использовать загруженную память (каждый 64-байтовый регистр используется дважды).

void mm32x32xK(float* A, float* B, float* C, uint64_t K) {

  // flag to load/store 128 bytes
  const uint64_t load_store_2 = 1ull << 62;
  const uint64_t load_store_width = 128; // in bytes

  // only set for k == 0
  uint64_t reset_z = 1ull << 27;

  for (uint32_t k = 0; k < K; ++k) {
    uint64_t idx = k % 4;
    // load to X, Y (skipping every other index because we're loading 128 bytes)
    AMX_LDX(load_store_2 | (idx * 2) << 56 | (uint64_t)A + k * load_store_width);
    AMX_LDY(load_store_2 | (idx * 2) << 56 | (uint64_t)B + k * load_store_width);

    // offset into X and Y registers is byte-wise
    const uint64_t offset = idx * load_store_width;

    // now we do 4 indepedent outer products (avoiding pipeline hazards)
    AMX_FMA32(reset_z | (0ull << 20) | ((offset +  0ull) << 10) | ((offset +  0ull) << 0));
    AMX_FMA32(reset_z | (1ull << 20) | ((offset + 64ull) << 10) | ((offset +  0ull) << 0));
    AMX_FMA32(reset_z | (2ull << 20) | ((offset +  0ull) << 10) | ((offset + 64ull) << 0));
    AMX_FMA32(reset_z | (3ull << 20) | ((offset + 64ull) << 10) | ((offset + 64ull) << 0));
    reset_z = 0;
  }

  for (uint64_t i = 0; i < 16; ++i) {
    // store interleaved
    AMX_STZ(load_store_2 | ((i * 4ull + 0) << 56) | (uint64_t)C + i * load_store_width);
    AMX_STZ(load_store_2 | ((i * 4ull + 2) << 56) | (uint64_t)C + (16 + i) * load_store_width);
  }
}

Выше я добавил комментарии, но есть еще пара интересных штук с флагами для инструкций. Corsix отлично все объясняет, поэтому я просто оставлю ссылки на объяснения:

• загрузка и хранение флагов;
• флаги FMA.

Как быстро мы к этому пришли? Ну, это зависит от числа килобайт, но к 1.5TFlops мы приходим при высоких значениях.

Не удивительно, что большие задачи получают лучшую относительную производительность, ведь у кеша больше возможностей для разогрева, а у процессора — для чередования инструкций.

В целом на фоне больших современных нейросетей, работающих с общим искусственным интеллектом, эти размеры просто микроскопические. Тем не менее такой тип производительности открывает двери и для меньших нейросетей, которые могут найти себе место в реальных современных вычислениях. Если прогноз можно выполнить на ноутбуке с питанием от батареи за пару десятков наносекунд, то, скорее всего, он имеет ценность больше, чем та ценность, которую мы могли бы добавить в местах, где иначе могла бы применяться эвристика.

Иными словами, по мнению автора, выполненный прогноз имеет ценность больше, чем та ценность, которой можно было бы добиться через эвристику.

А что думаете по этому поводу вы? Спасибо за внимание!

• Профессия Data Scientist (25 месяцев)
• Профессия Fullstack-разработчик на Python (16 месяцев)