В производстве все больше используется оборудование с числовым программным управлением (программным обеспечением). И все большую роль приобретают 3D-принтеры и 3D-сканеры (оптические, лазерные). На вход в 3D-принтеры подаются модели формата *.stl – STL модель, на выходе из 3D-сканеров создаётся модель реального объекта в формате *.stl. Модель формата *.stl представляет собой пространственную триангуляционную сетку, поверхность из множества треугольников. Для анализа геометрии деталей по STL и построении из STL твердотельных компьютерных моделей необходимо разбить единую триангуляционную поверхность на отдельные грани.
В программных продуктах для работы с STL, таких как Geomatix Design X, Wrap, NX и др., функционал обязательно включает сегментацию STL модели на отдельные грани. На рисунке 1 приведён пример сегментации STL модели секции лопаток соплового аппарата (часть газовой турбины).

В свободно распространяемом ПО, однако, инструменты для сегментации зачастую отсутствуют. В данной статье хочу рассказать о реализованном мной на Python алгоритме разбиения STL на отдельные грани.
Кратко об STL
Для триангуляционной сетки введём следующие обозначения матриц, характеризующих её: Vg×3 – матрица координат вершин сетки stl-модели, Fm×3 – матрица сочетаний вершин в фасеты (состоит из трех столбцов Fa, Fb, Fc), Nm×3 – матрица координат нормалей фасет. Каждая точка регулярной поверхности в трёхмерном евклидовом пространстве характеризуется двумя экстремальными значениями кривизн kmin и kmax, называемых главными [1]. Вычисление главных кризн основано на вычислении производных, и для поверхности STL, которая является кусочно-линейной, вычисление главных кривизн является нетривиальной задачей. Для корректного вычисления кривизн еще в начале текущего века были разработаны различные подходы [2, 3, 4]. В моей реализации я опирался на работу [3] для вычисления кривизн. В алгоритмах сегментации используются значениями кривизн и направлениями нормалей для разделения граней, реализованный мною алгоритм не является исключением.
Математика алгоритма сегментации
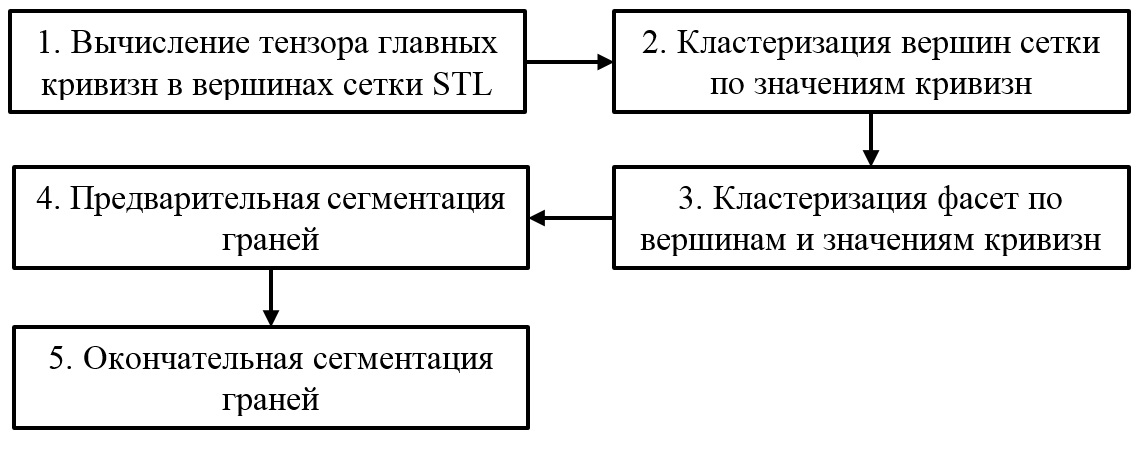
Блок-схема алгоритма сегментации stl-моделей на ряд областей приведена на рисунке 2.
На первом этапе разработанного алгоритма, при вычислении главных кривизн в вершинах stl моделей были использованы результаты работы [3]. Тензор главных кривизн представляет собой значения самих главных кривизн (собственные числа тензора) и главные направления изменения этих кривизн (собственные векторы тензора). Приведём кратко последовательность вычислений параметров тензора.
Сначала вычисляются все вектора граней фасет (запишем их в виде матриц):
Вектора граней нормируются. С использованием компонент матрицы Nm×3 для каждой фасеты вычисляются три угла фасеты, видимых из вершины, как арккосинус скалярного произведения: Нормали каждой фасеты вычисляется как векторное произведение двух векторов граней фасеты.
Компоненты нормалей Nx, Ny, Nz в каждой вершине находятся как сумма произведений компонент нормали фасеты и соответствующего угла. Компоненты нормируются.
На следующем этапе рассчитываются компоненты матриц повората для нормали – Mr3×3 , так чтобы она имела компоненты [-1, 0, 0]. Кроме того, рассчитываются компоненты обратной матрицы для возврата в исходную систему координат. Для каждой вершины находится вектор порядковых номеров соседних вершин первого и второго уровней – формируется матрица координат этих вершин Vn×3. С вершинами первого уровня она связана ребрами, второй уровень образован соседями вершин первого уровня. Для поиска вершин используется матрица Fm×3.
Вершины в окрестности поворачиваются, то есть производится умножение матриц Vn×3 иMr3×3. Для повернутых точек подбираются коэффициенты полинома второй степени: , где
– координаты вершин окрестности. Формируется матрица:
.
Далее вычисляют собственно собственные числа и
(главные кривизны) и собственные векторы
и
тензора главных кривизн.
,
, где
.
,
ортогонален
.
и
нормируются.
На втором этапе алгоритма выполнялась кластеризация вершин сетки по значениям главных кривизн и
. Алгоритм кластеризации вершин основан на методе машинного обучении без учителя – методе k-средних. Алгоритм k-средних выполняет поиск заранее заданного количества кластеров в немаркированном многомерном наборе данных [5]. Результаты кластеризации достигаются итерационно, основываясь на двух допущениях: 1) «центр кластера» — арифметическое среднее всех точек, относящихся к этому кластеру 2) каждая точка ближе к центру своего кластера, чем к центрам других кластеров. В рассматриваемом объекте (сочетание четырёх поверхностей) количество кластеров явно следует задать равным четырём.
На третьем этапе алгоритма классифицируются сами фасеты. Классификация фасет происходит уже по сочетанию главных кривизн в вершинах фасета. Вначале данной процедуры выявляются все фасеты, у которых вершины принадлежат одному кластеру и не превышают поставленный допуск на кривизну, задаваемый в начале алгоритма. Такие фасеты являются полностью определенными (относящимися к определенному кластеру) [6]. Параметр кривизны каждой полностью определенной фасеты рассчитывается по формуле:
где ,
– кривизны фасеты;
,
– главные кривизны i-й вершины фасеты.
Данные по допуску на кривизну для каждого конкретного объекта и по количеству кластеров для предыдущего этапа можно получать автоматизировано по результатам классификации детали, или задать вручную.
Кроме рассмотренного ранее случая, существуют еще четыре типа фасет с точки зрения классификации по кривизнам в вершинах. Будем называть вершину «острой», если значение одной из двух главных кривизн превышает заданный допуск на кривизну всех поверхностей. На рисунке 3 приведено пояснение к оставшимся четырем группам с точки зрения наличия «острых вершин».
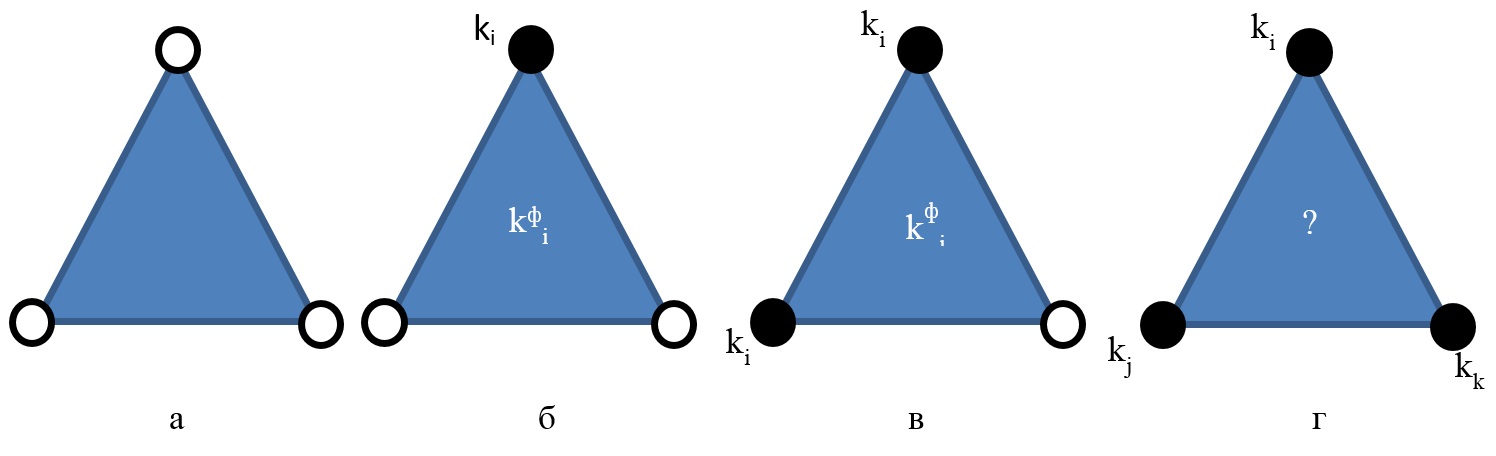
В первой группе фасет (рисунок 3, а) все три вершины фасеты являются «острыми». В данном случае кривизна фасеты определяется так же по выражению (3). Для разделения фасет по классам производится расчет евклидовых расстояний между вектором кривизн фасеты и векторами центров кластеров:
где – вектор главных кривизн i-го кластера.
Выбирается кластер, для которого евклидово расстояние (4) минимально. Кривизна фасеты приравнивается к вектору кривизн кластера, к которому она была определена.
Во второй группе фасет (рисунок 3, б) две вершины являются «острыми». Кривизна фасеты приравнивается к кривизне не «острой» вершины, фасета отходит в класс этой вершины.
В третьей группе фасет (рисунок 3, в) одна вершина «острая». В этой группе также возможно два варианта: оставшиеся две фасеты принадлежат одному классу; оставшиеся две вершины принадлежат разным классам. В обоих случаях кривизна фасеты определяется по выражению (2), только в вычислении учавствуют не «острые» вершины. Определение класса осуществляется аналогично как в первой группе (рисунок 3, а).
В четвертой группе фасет (рисунок 3, г) нет «острых» вершин, но вершины принадлежат разным классам. Определение принадлежности к тому или иному классу осуществляется аналогично первой группе (рисунок 3, а).
Четвертым этапом алгоритма является процесс предварительной сегментации фасет. В нем классифицированные на предыдущем этапе фасеты объединяются (разрастаются) до участков фасет. Объединение осуществляется внутри классов, где выбирается случайным образом начальная фасета. Если по абсолютной величине хотя бы одна из кривизн фасеты превышают некую величину , близкую к 0, то в качестве метрики объединения
выступает вектор кривизн. Если обе близки к 0, то видимо имеет место плоский участок (плоская грань), и в качестве метрики для объединения фасет выступает вектор нормали
. Допуск на отклонение нормали
в угловом выражении так же задается пользователем.
После определения метрики выбираются смежные с выбранным треугольники до тех пор, пока разница между их метриками объединения с целевой метрикой не превысит допуска. Производится поиск всех фасет, у которых разница между их метриками объединения с целевой метрикой вектор нормали не превышает величину допуска (для кривизн рассчитывается эвклидово расстояние, аналогично (4); в случае нормалей используется скалярное произведение векторов).
Из множества находящихся в заданном допуске фасет производится выбор фасет, связанных с первой и между собой общими вершинами.
Завершающим этапом является алгоритм окончательной сегментации фасет. Целью этапа является: 1) уменьшение чрезмерной сегментации, возникшей на четвертом этапе; 2) сделать алгоритм сегментации независимым от количества кластеров кривизны после классификации вершин на втором этапе. Таким образом, на завершающем этапе происходит объединение смежных однородных областей фасет, полученных в результате выполнения четвертого этапа. Математика для выполнения этого этапа взята из работы [6].
Эффективность алгоритма зависит от используемой схемы данных, была использовано представление данных по уже сегментированным участком в виде графа смежности областей (RAG), используемая при сегментации изображений [7].
Выявляется область с наибольшей площадью. Затем вычисляется общая граница (граф смежности) с соседними областями и вычисляются расстояния между целевой областью и соседями по формуле:
,
где – расстояние по кривизне меду двумя областями, равное сумме расстояний между векторами кривизн участков и кривизны их границы;
– коэффициент, вычисляемый как отношение минимального из периметров границ двух областей к длине их общей границы;
– коэффициент ускорения поглощения очень малых областей, основанный на использовании величин площадей поверхности областей
,
и допуска
:
Расстояние по кривизне сравнивается с допуском на объединение областей, который равен допуска , умноженному на поправочный коэффициент. Если расстояние меньше допуска, то области объединяются. Алгоритм проходит последовательно по всем областям, от наибольшего к наименьшему, постепенно объединяя однородные участки. Формируется структура сегментированных областей Fc (величина совпадает с матрицей фасет тела Fm×3).
Реализация алгоритма на Python
Я реализовывал алгоритм сегментации на Python версии 3.8.8. Кроме того, для выполнения ряда операций и визуализаций решения понадобятся следующие библиотеки: trimesh версии 3.19.4; vedo версии 2023.4.3; numpy версии 1.22.4 для выполнения матричных операций; matplotlib 3.3.0 для визуализации; scipy 1.6.2 для сохранения каждого из пяти этапов в файлы формата *.mat; scikit-learn версии 0.24.2 для выполнения кластеризации.
Полный исходный код находится в репозитории https://github.com/vadimpechenin/segmentation_method_of_stl_objects_2020.git.
Для хранения всей
необходимой информации о сетке STL и параметров, хранящих информацию о
сегментации, был создан класс Mesh_class.
class Mesh_class():
"""Класс slt-объекта"""
def __init__(self,num_vertices,num_faces):
self.num_vertices = num_vertices
self.num_faces = num_faces
self.vertices =0
self.faces = 0
self.normals =0
self.Cmin = 0
self.Cmax = 0
#Структура сегментированныой сетки
# В виде списков с вложенными матрицами
# Структура фасет сегментов
self.surface_seg = 0
# Структура нормалей фасет сегментов
self.surfaceNormal_seg = 0
# Структура кривизн фасет сегментов
self.surfaceCurve_seg = 0
# В виде матриц
# Площади сегментов
self.area_segments = 0
# Количество фасет в каждом сегменте
self.num_segments = 0
# Общая кривизна каждого сегмента
self.curve_of_segments = 0
# Число, отвечающее за цвет каждого сегмента
self.color_segments = 0
# Количество сегментов
self.struct_seg = 0 Для хранения настроек алгоритма был создан класс Main_variables. В классе храняться значения переменный pl_zagr, отвечающая за выполнение или загрузку каждого из этапов; переменной pl, отвечающей за визуализацию результатов каждого из этапов; переменной curvature_tolerance для хранения величины допуска на кривизну и переменной angle_tolerance, для хранения величины допуска на угол(при работе с разбиением плоских граней).
class Main_variables():
"""Класс, в котором храняться главные переменные проекта"""
def __init__(self):
self.pl_zagr = np.array([0, 0, 0, 0, 0])
""" Переменная выполнения этапов 1-5
1 этап - загрузка структуры stl
2 этап - вычисление кривизн поверхности
3 этап - кластеризация вершин по кривизне, предварительная классификация фасет
4 этап - предварительная сегментация фасет
5 этап - окончательная сегментация фасет
6 этап - визуализация без мелких деталей"""
self.pl = np.array([0, 0, 0, 1, 1, 1]) # Прорисовка этапов 1-5
self.pl_sphere_cyl = np.array([5, 1]) # 1 - какая серия эксперментов; 2 - вид из серии экспериментов
self.pl_klast = 1 # какой алгоритм кластеризации использовать, k-mean или DBSCAN
self.curvature_tolerance = 0.6 # допуск на кривизну при кластеризации
self.angleTolerance = 30
self.path_file = 'D:\\PYTHON\\Programms\\Segmentation_ex_2\\Segmentation_stl_py_2020\\results\\'Сначала осуществляется импорт матриц, характеризующих STL. Выполняется это в классе Import_stl_data, с помощью единственного его метода import_data. Для импорта используется метод load библиотеки trimesh. В Mesh_class заполняются поля num_vertices, num_faces, vertices, faces , normal. Структуры struct_seg, num_segments и color_segmetns на этом этапе заданы в виде единичных матриц из одного элемента. Матрица surface_seg задана в виде двумерного списка, в единственном элементе которого помещается значение структуры faces.
В качестве примера работы алгоритма используем сетку, состоящую из 5232 вершин и 10460 граней. Код для визуализации приведен ниже (используется библиотека trimesh).
def plot_stl_color(struct_seg,num_segments, surface_seg,vertices):
# https://pydoc.net/trimesh/2.22.26/trimesh.visual/
#https://pypi.org/project/trimesh/
"""Функция для прорисовки stl объекта"""
# struct_seg - структура участков (если поверхность сегментирована, то больше 1)
# num_segments - структура количества фасет
# surface_seg - фасеты, из которых состоит каждый участок
# vertices - общий набор вершин поверхности
if (1 == 1):
# C Использованием библеотеки trimesh
for j in range(struct_seg.shape[0]):
for i in range(num_segments.shape[0]):
faces = copy.deepcopy(surface_seg[j][i][0])
meshFromTrimesh = trimesh.Trimesh(vertices=vertices,
faces=faces,
process=False)
# Если объект один
if (struct_seg.shape[0] == 1) & (num_segments.shape[0] == 1):
meshFromTrimesh.visual.face_colors = [200, 200, 250]
else:
facet = range(faces.shape[0])
meshFromTrimesh.visual.face_colors[facet] = trimesh.visual.random_color()
meshFromTrimesh.show()Результат визуализации приведен на рисунке 4.

Объект состоит из трех сфер разного диаметра, между двумя из них выполнено скругление места сопряжения.
С использованием методов библиотеки scipy.io – savemat и loadmat результаты работы каждого из этапов сохраняются в виде словарей в файлы *.mat, удобные для хранения матриц чисел.
После загрузки и сохранения структуры сетки можно приступать собственно к этапам сегментации. Ниже приведён код для вычисления главных кривизн.
def patchcurvature_2014(mesh):
#1. Количество вершин
num_vertices=mesh.vertices.shape[0]
# 2. Расчет нормалей в вершинах
normals_in_vertices = patchnormals(mesh)
# 3. Расчет матриц вращения для нормалей
M = np.zeros([3, 3, num_vertices])
Minv = np.zeros([3, 3, num_vertices])
for i in range(num_vertices):
M[:,:, i], Minv[:,:, i]=VectorRotationMatrix(normals_in_vertices[i,:])
# 4. Получить соседей всех вершин
neighbours_of_vetres=vertex_neighbours(mesh)
# Перебрать все вершины
min_curvature = np.zeros([num_vertices, 1])
max_curvature = np.zeros([num_vertices, 1])
Dir1 = np.zeros([num_vertices, 3])
Dir2 = np.zeros([num_vertices, 3])
for i in range(num_vertices):
# Получение соседей первого и второго уровней.
idx_1_2_ring=np.array(neighbours_of_vetres[i])
neighbours_of_vetres_1_2_ring=np.array([]).astype(int)
for j in idx_1_2_ring:
c=np.array(neighbours_of_vetres[int(j)])
neighbours_of_vetres_1_2_ring = np.append(neighbours_of_vetres_1_2_ring,c)
neighbours_of_vetres_1_2_ring=np.unique(neighbours_of_vetres_1_2_ring)
vert_no_rot=mesh.vertices[neighbours_of_vetres_1_2_ring,:]
# Вращение вершин, чтобы сделать нормаль [-1 0 0]
c=Minv[:,:,i]
vert_rot=np.dot(vert_no_rot, Minv[:,:,i])
f , x, y = vert_rot[:, 0], vert_rot[:, 1], vert_rot[:, 2]
# Вписать фасеты в уравнение второй степени
# f(x,y) = ax^2 + by^2 + cxy + dx + ey + f
function_of_curve = np.array([x[:]** 2, y[:]** 2, x[:]*y[:], x[:], y[:], np.ones([vert_rot.shape[0]])]).T
abcdef=np.linalg.lstsq(function_of_curve,f)
a, b, c = abcdef[0][0], abcdef[0][1], abcdef[0][2]
# Создание матрицы Гессиана
# H = [2*a c;c 2*b]
Dxx, Dxy, Dyy = 2 * a, c, 2 * b
min_curvature[i], max_curvature[i], I1, I2 = eig2(Dxx, Dxy, Dyy)
dir1 = np.dot(np.array([0, I1[0], I1[1]]), M[:, :, i])
dir2 = np.dot(np.array([0, I2[0], I2[1]]), M[:, :, i])
Dir1[i,:]=dir1 / (dir1[0] ** 2 + dir1[1] ** 2 + dir1[2] ** 2) ** (0.5)
Dir2[i,:]=dir2 / (dir2[0] ** 2 + dir2[1] ** 2 + dir2[2] ** 2) ** (0.5)
return Dir1, Dir2, min_curvature, max_curvature
def patchnormals(mesh):
# Функция вычисления нормалей триангуляционной сетки.
# Вызывается функция patchnormals_double, вычисляющая нормали всех граней, а затем нормали вершин по нормалям
# граней, взвешенным по углам граней
Nx, Ny, Nz = patchnormals_double(mesh.faces[:, 0], mesh.faces[:, 1],
mesh.faces[:, 2], mesh.vertices[:, 0].astype('float32'),
mesh.vertices[:, 1].astype('float32'), mesh.vertices[:, 2].astype('float32'))
normals_in_vertices = np.zeros([Nx.shape[0], 3])
normals_in_vertices[:, 0]=Nx
normals_in_vertices[:, 1]=Ny
normals_in_vertices[:, 2]=Nz
return normals_in_vertices
def patchnormals_double(Fa,Fb,Fc,Vx,Vy,Vz):
# Функция вычисления составляющих нормалей в вершинах stl
vertices = np.zeros([Vx.shape[0], 3])
vertices[:, 0]=Vx
vertices[:, 1]=Vy
vertices[:, 2]=Vz
# 1. Вычисление всех векторов граней
e1 = vertices[Fa,:]-vertices[Fb,:]
e2 = vertices[Fb,:]-vertices[Fc,:]
e3 = vertices[Fc,:]-vertices[Fa,:]
# Нормирование векторов
e1_norm = np.array([e1[:,0] / (e1[:, 0] ** 2 + e1[:, 1] ** 2 + e1[:, 2] ** 2)** (0.5),
e1[:, 1] / (e1[:, 0] ** 2 + e1[:, 1] ** 2 + e1[:, 2] ** 2) ** (0.5),
e1[:, 2] / (e1[:, 0] ** 2 + e1[:, 1] ** 2 + e1[:, 2] ** 2) ** (0.5)]).T
e2_norm =np.array([e2[:,0] / (e2[:, 0] ** 2 + e2[:, 1] ** 2 + e2[:, 2] ** 2)** (0.5),
e2[:,1] / (e2[:, 0] ** 2 + e2[:, 1] ** 2 + e2[:, 2] ** 2) ** (0.5),
e2[:,2] / (e2[:, 0] ** 2 + e2[:, 1] ** 2 + e2[:, 2] ** 2) ** (0.5)]).T
e3_norm = np.array([e3[:,0] / (e3[:, 0] ** 2 + e3[:, 1] ** 2 + e3[:, 2] ** 2)** (0.5),
e3[:,1] / (e3[:, 0] ** 2 + e3[:, 1] ** 2 + e3[:, 2] ** 2) ** (0.5),
e3[:,2] / (e3[:, 0] ** 2 + e3[:, 1] ** 2 + e3[:, 2] ** 2) ** (0.5)]).T
# 2. Расчет угла фасет, видимых из вершин
# равносильно np.multiply(e1_norm.T,-e3_norm.T)==e1_norm.T*(-e3_norm.T)
Angle = np.array([np.arccos(np.sum(np.multiply(e1_norm.T,-e3_norm.T),axis=0)),
np.arccos(np.sum(np.multiply(e2_norm.T,-e1_norm.T),axis=0)),
np.arccos(np.sum(np.multiply(e3_norm.T,-e2_norm.T),axis=0))]).T
# 3. Расчет нормалей граней
normals_of_faces=np.cross(e1,e3)
# 4. Расчет нормалей в вершинах
normals_in_vertices = np.zeros([Vx.shape[0], 3])
for i in range(Fa.shape[0]):
normals_in_vertices[Fa[i],:]=normals_in_vertices[Fa[i],:]+normals_of_faces[i,:]*Angle[i, 0]
normals_in_vertices[Fb[i],:]=normals_in_vertices[Fb[i],:]+normals_of_faces[i,:]*Angle[i, 1]
normals_in_vertices[Fc[i],:]=normals_in_vertices[Fc[i],:]+normals_of_faces[i,:]*Angle[i, 2]
eps=1/10000000000000000
V_norm = (normals_in_vertices[:, 0] ** 2 + normals_in_vertices[:, 1] ** 2 +
normals_in_vertices[:, 2] ** 2) ** (0.5) + eps
Nx = normals_in_vertices[:, 0] / V_norm
Ny = normals_in_vertices[:, 1] / V_norm
Nz = normals_in_vertices[:, 2] / V_norm
return Nx, Ny, Nz
def VectorRotationMatrix(normals_in_vertices):
# Функция расчета матрицы вращения и обратной ей
v = (normals_in_vertices.T) / (np.sum(normals_in_vertices**2))**(0.5)
k = np.array([random.random() for i in range(3)])
l = np.array([k[1] * v[2] - k[2] * v[1], k[2] * v[0] - k[0] * v[2], k[0] * v[1] - k[1] * v[0]])
l = l / (np.sum(l ** 2))**(0.5)
k = np.array([l[1] * v[2] - l[2] * v[1], l[2] * v[0] - l[0] * v[2], l[0] * v[1] - l[1] * v[0]])
k = k / (np.sum(k ** 2))**(0.5)
Minv = np.array([v, l, k]).T
M = np.linalg.inv(Minv)
return M, Minv
def vertex_neighbours(mesh):
# Эта функция производит поиск всех фасет-соседей каждой вершины в списке фасет поверхности.
neighbours_of_vetres = vertex_neighbours_double(mesh.faces[:, 0], mesh.faces[:, 1],
mesh.faces[:, 2], mesh.vertices[:, 0],
mesh.vertices[:, 1], mesh.vertices[:, 2])
return neighbours_of_vetres
def vertex_neighbours_double(Fa,Fb,Fc,Vx,Vy,Vz):
faces = np.array([Fa, Fb, Fc]).T
vertex= np.array([Vx, Vy, Vz]).T
# массив соседей вершин
neighbours_of_vetres = []
for r in range(vertex.shape[0]):
neighbours_of_vetres.append([])
# Пройтись по всем фасетам
for i in range(faces.shape[0]):
# Добавить соседей каждой вершины фасеты в список соседей.
neighbours_of_vetres[faces[i, 0]].append(faces[i, 1])
neighbours_of_vetres[faces[i, 0]].append(faces[i, 2])
neighbours_of_vetres[faces[i, 1]].append(faces[i, 2])
neighbours_of_vetres[faces[i, 1]].append(faces[i, 0])
neighbours_of_vetres[faces[i, 2]].append(faces[i, 0])
neighbours_of_vetres[faces[i, 2]].append(faces[i, 1])
# Перебрать все соседние массивы и отсортировать их (Поворот такой же, как у фасет)
for i in range(vertex.shape[0]):
Pneighf=neighbours_of_vetres[i]
Pneig = []
if (len(Pneighf)==0):
pass
else:
for x in Pneighf:
if x not in Pneig:
Pneig.append(x)
neighbours_of_vetres[i] = Pneig
return neighbours_of_vetres
def eig2(Dxx, Dxy, Dyy):
# | Dxx Dxy |
# | |
# | Dxy Dyy |
# Вычисление собственных векторов
tmp = ((Dxx - Dyy)** 2 + 4 * Dxy**2)**(0.5)
v2x, v2y = 2 * Dxy, Dyy - Dxx + tmp
# Нормализация
mag = (v2x** 2 + v2y** 2)**(0.5)
if (mag != 0):
v2x = v2x / mag
v2y = v2y / mag
# Собственные векторы ортогональны
v1x = -copy.deepcopy(v2y)
v1y = copy.deepcopy(v2x)
# Вычисление собственных значений
mu1 = (0.5 * (Dxx + Dyy + tmp))
mu2 = (0.5 * (Dxx + Dyy - tmp))
# Сортировка собственных значений по абсолютному значению abs (Lambda1) < abs(Lambda2)
if (abs(mu1) < abs(mu2)):
min_curvature = mu1
max_curvature = mu2
I2 = np.array([v1x, v1y])
I1 = np.array([v2x, v2y])
else:
min_curvature = mu2
max_curvature = mu1
I2 = np.array([v2x, v2y])
I1 = np.array([v1x, v1y])
return min_curvature, max_curvature, I1, I2На рисунке 5 приведена визуализация значений в вершинах рассматриваемой сетки.
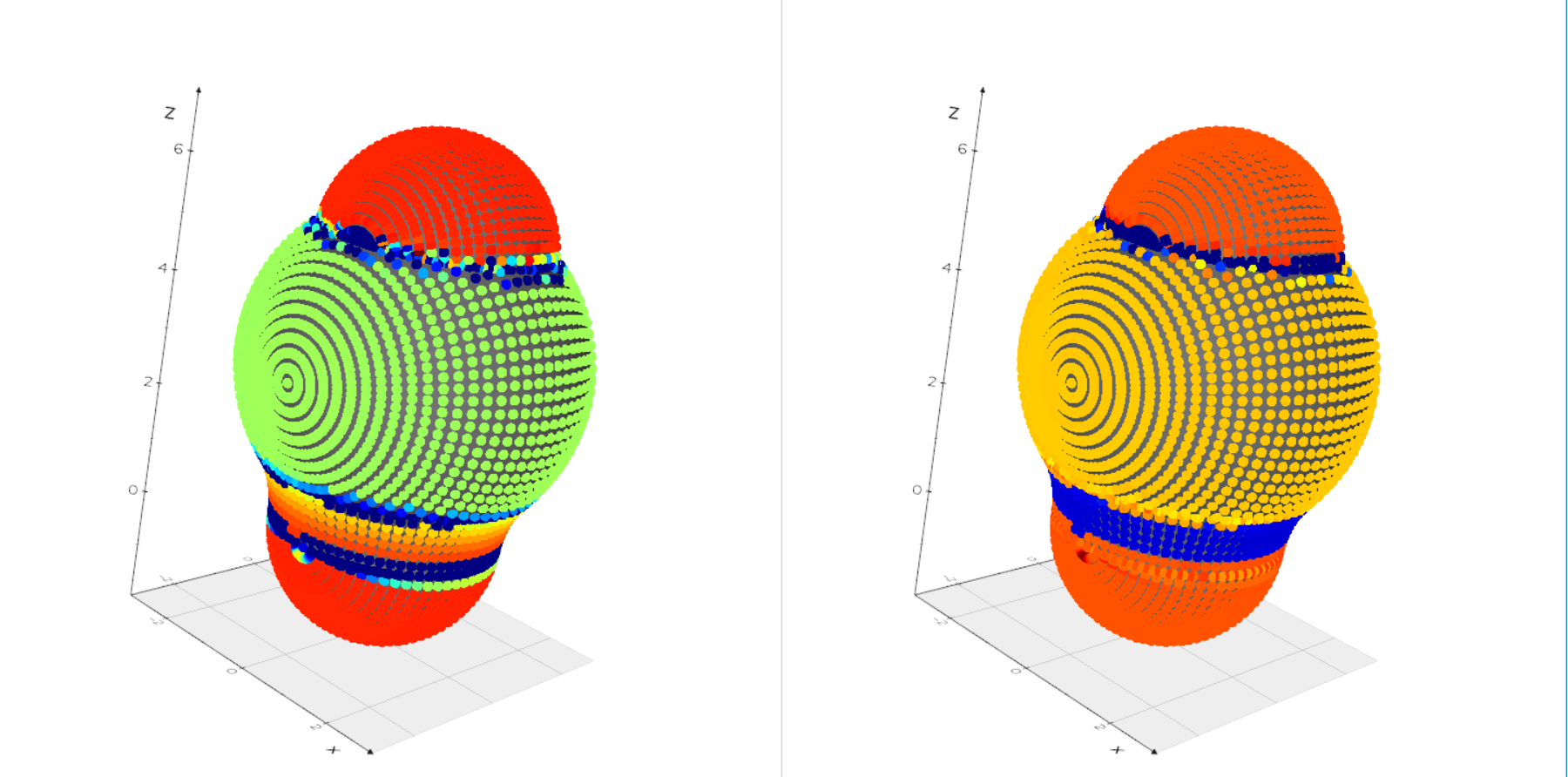
Второй и третий этапы алгоритма объединены в одной функции. Кластеризация вершин по двум значениям кривизн выполняется с использованием класса KMeans библиотеки scikit-learn.
def klastering_vetices_of_mesh_by_curvature_tensor(mesh,pl_zagr,pl,pl_sphere_cyl,path_file,curvature_tolerance):
# Количество кластеров
N_clusters=sff.num_of_klasters(pl_sphere_cyl)
X = np.zeros([mesh.Cmin.shape[0], 2])
# Нормирование для кластеризации
Cmin1, Cmax1 = copy.deepcopy(mesh.Cmin), copy.deepcopy(mesh.Cmax)
min_max_Cmin = np.array([np.mean(mesh.Cmin) - np.std(mesh.Cmin), np.mean(mesh.Cmin) + np.std(mesh.Cmin)])
min_max_Cmax = np.array([np.mean(mesh.Cmax) - np.std(mesh.Cmax), np.mean(mesh.Cmax) + np.std(mesh.Cmax)])
for i in range(mesh.Cmin.shape[0]):
if Cmin1[i] > min_max_Cmin[1]:
Cmin1[i] = min_max_Cmin[1]
elif Cmin1[i] < min_max_Cmin[0]:
Cmin1[i] = min_max_Cmin[0]
if Cmax1[i] > min_max_Cmax[1]:
Cmax1[i] = min_max_Cmax[1]
elif Cmax1[i] < min_max_Cmax[0]:
Cmax1[i] = min_max_Cmax[0]
X[:, 0], X[:, 1] = copy.deepcopy(Cmin1[:, 0]), copy.deepcopy(Cmax1[:, 0])
if (pl_zagr[2] == 1):
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=N_clusters)
kmeans.fit(X)
idx_K = kmeans.predict(X)
centers = kmeans.cluster_centers_
# 2. Выявляем зерна (по двум кривизнам)
massiv_face_klast = np.full((mesh.faces.shape[0], 1), -1)
curvature_null = np.array([np.amax(mesh.Cmin) + 100, np.amax(mesh.Cmax) + 100])
curvature_face_klast = np.full((mesh.faces.shape[0], 2), curvature_null)
curvature_mean = np.zeros([N_clusters, 2])
for j in range(centers.shape[0]):
w = idx_K[mesh.faces[:, 0]]
idx_K_1, = np.where(idx_K[mesh.faces[:, 0]] == j)
idx_K_2, = np.where(idx_K[mesh.faces[:, 1]] == j)
idx_K_3, = np.where(idx_K[mesh.faces[:, 2]] == j)
# 2. intersection
C1 = np.intersect1d(idx_K_1, idx_K_2)
C2 = np.intersect1d(idx_K_2, idx_K_3)
C3 = np.intersect1d(C1, C2)
if C3.shape[0] > 0:
massiv_face_klast[C3, 0] = j
curvature_face_klast[C3, 0], curvature_face_klast[C3, 1] = mesh.Cmin[mesh.faces[C3, 0], 0], \
mesh.Cmax[mesh.faces[C3, 0], 0]
curvature_mean[j, :] = np.mean(curvature_face_klast[C3, :], axis=0)
# Выявляем границы и идентифицируем их
id, = np.where(curvature_face_klast[:, 0] == curvature_null[0])
# Массив кривизн смешанных граней
f_K_1, f_K_2 = np.zeros((id.shape[0], 3)), np.zeros((id.shape[0], 3))
f_K_1[:, 0], f_K_1[:, 1], f_K_1[:, 2] = copy.deepcopy(mesh.Cmin[mesh.faces[id, 0], 0]), \
copy.deepcopy(mesh.Cmin[mesh.faces[id, 1], 0]), \
copy.deepcopy(mesh.Cmin[mesh.faces[id, 2], 0])
f_K_2[:, 0], f_K_2[:, 1], f_K_2[:, 2] = copy.deepcopy(mesh.Cmax[mesh.faces[id, 0], 0]), \
copy.deepcopy(mesh.Cmax[mesh.faces[id, 1], 0]), \
copy.deepcopy(mesh.Cmax[mesh.faces[id, 2], 0])
# Нулевой массив
f_K_1_null, f_K_2_null = np.zeros((id.shape[0], 3)), np.zeros((id.shape[0], 3))
idx_K_1_f1, idx_K_1_f_alt1 = np.where(abs(f_K_1[:, 0]) > curvature_tolerance), \
np.where(abs(f_K_1[:, 0]) <= curvature_tolerance)
idx_K_2_f1, idx_K_2_f_alt1 = np.where(abs(f_K_1[:, 1]) > curvature_tolerance), \
np.where(abs(f_K_1[:, 1]) <= curvature_tolerance)
idx_K_3_f1, idx_K_3_f_alt1 = np.where(abs(f_K_1[:, 2]) > curvature_tolerance), \
np.where(abs(f_K_1[:, 2]) <= curvature_tolerance)
idx_K_1_f2, idx_K_1_f_alt2 = np.where(abs(f_K_2[:, 0]) > curvature_tolerance), \
np.where(abs(f_K_2[:, 0]) <= curvature_tolerance)
idx_K_2_f2, idx_K_2_f_alt2 = np.where(abs(f_K_2[:, 1]) > curvature_tolerance), \
np.where(abs(f_K_2[:, 1]) <= curvature_tolerance)
idx_K_3_f2, idx_K_3_f_alt2 = np.where(abs(f_K_2[:, 2]) > curvature_tolerance), \
np.where(abs(f_K_2[:, 2]) <= curvature_tolerance)
# Объединение union
idx_K_1_f, idx_K_1_f_alt = np.union1d(idx_K_1_f1, idx_K_1_f2), np.union1d(idx_K_1_f_alt1, idx_K_1_f_alt2)
idx_K_2_f, idx_K_2_f_alt = np.union1d(idx_K_2_f1, idx_K_2_f2), np.union1d(idx_K_2_f_alt1, idx_K_2_f_alt2)
idx_K_3_f, idx_K_3_f_alt = np.union1d(idx_K_3_f1, idx_K_3_f2), np.union1d(idx_K_3_f_alt1, idx_K_3_f_alt2)
f_K_2_null[idx_K_1_f, 0] = curvature_null[1]
f_K_2_null[idx_K_2_f, 1] = curvature_null[1]
f_K_2_null[idx_K_3_f, 2] = curvature_null[1]
# Ищем где 2 острых грани, или 1, или 0
# Делаем свертку матрицы, ищем строчки с ситуациями
f_K_2_null_svertka = np.sum(f_K_2_null, axis=1)
# 3 острых вершины
id_3_versh = np.where(f_K_2_null_svertka == 3 * (curvature_null[1]))
# 2 острых вершины
id_2_versh = np.where(f_K_2_null_svertka == 2 * (curvature_null[1]))
# 1 острая вершина
id_1_versh = np.where(f_K_2_null_svertka == (curvature_null[1]))
# 0 острых вершин
id_0_versh = np.where(f_K_2_null_svertka == 0)
# Поиск кривизн треугольников
# Нулевой массив для записи кривизн не острых вершинами в фасетах с острыми вершинами
f_K_1_null2, f_K_2_null2 = np.zeros((id.shape[0], 3)), np.zeros((id.shape[0], 3))
# Специально когда все 3 острые вершины
f_K_1_null3, f_K_2_null3 = np.zeros((id.shape[0], 3)), np.zeros((id.shape[0], 3))
# Свертка значений в 1 число
f_K_1_null_svertka, f_K_2_null_svertka = np.zeros((id.shape[0], 1)), np.zeros((id.shape[0], 1))
# Матрица разностей для поиска кластера
delt_kriv = np.zeros((id.shape[0], centers.shape[0]))
# массив кривизн
f_K_1_null2[idx_K_1_f_alt, 0] = mesh.Cmin[mesh.faces[id[idx_K_1_f_alt], 0], 0]
f_K_1_null2[idx_K_2_f_alt, 1] = mesh.Cmin[mesh.faces[id[idx_K_2_f_alt], 1], 0]
f_K_1_null2[idx_K_3_f_alt, 2] = mesh.Cmin[mesh.faces[id[idx_K_3_f_alt], 2], 0]
f_K_2_null2[idx_K_1_f_alt, 0] = mesh.Cmax[mesh.faces[id[idx_K_1_f_alt], 0], 0]
f_K_2_null2[idx_K_2_f_alt, 1] = mesh.Cmax[mesh.faces[id[idx_K_2_f_alt], 1], 0]
f_K_2_null2[idx_K_3_f_alt, 2] = mesh.Cmax[mesh.faces[id[idx_K_3_f_alt], 2], 0]
f_K_1_null3[idx_K_1_f, 0] = mesh.Cmin[mesh.faces[id[idx_K_1_f], 0], 0]
f_K_1_null3[idx_K_2_f, 1] = mesh.Cmin[mesh.faces[id[idx_K_2_f], 1], 0]
f_K_1_null3[idx_K_3_f, 2] = mesh.Cmin[mesh.faces[id[idx_K_3_f], 2], 0]
f_K_2_null3[idx_K_1_f, 0] = mesh.Cmax[mesh.faces[id[idx_K_1_f], 0], 0]
f_K_2_null3[idx_K_2_f, 1] = mesh.Cmax[mesh.faces[id[idx_K_2_f], 1], 0]
f_K_2_null3[idx_K_3_f, 2] = mesh.Cmax[mesh.faces[id[idx_K_3_f], 2], 0]
# 0 случай, 3 острые вершины (судя или по 1 или по 2 кривизне)
if (len(id_3_versh[0]) > 0):
f_K_1_null_svertka[id_3_versh, 0] = np.sum(f_K_1_null3[id_3_versh[0], :], axis=1) / 3
f_K_2_null_svertka[id_3_versh, 0] = np.sum(f_K_2_null3[id_3_versh[0], :], axis=1) / 3
for j in range(centers.shape[0]):
delt_kriv[id_3_versh, j] = ((f_K_1_null_svertka[id_3_versh, 0] -
np.full((1, len(id_3_versh[0])), centers[j, 0])) ** 2 +
(f_K_1_null_svertka[id_3_versh, 0] -
np.full((1, len(id_3_versh[0])), centers[j, 1])) ** 2) ** 0.5
num_center_of_sharp = np.argmin(delt_kriv[id_3_versh[0], :], axis=1).T
massiv_face_klast[id[id_3_versh], 0] = num_center_of_sharp.T
curvature_face_klast[id[id_3_versh], 0] = f_K_1_null_svertka[id_3_versh, 0]
curvature_face_klast[id[id_3_versh], 1] = f_K_2_null_svertka[id_3_versh, 0]
# 1 случай, 2 острые вершины
if (len(id_2_versh[0]) > 0):
f_K_1_null_svertka[id_2_versh, 0] = np.sum(f_K_1_null3[id_2_versh[0], :], axis=1)
f_K_2_null_svertka[id_2_versh, 0] = np.sum(f_K_2_null3[id_2_versh[0], :], axis=1)
for j in range(centers.shape[0]):
delt_kriv[id_2_versh, j] = ((f_K_1_null_svertka[id_2_versh, 0] -
np.full((1, len(id_2_versh[0])), centers[j, 0])) ** 2 +
(f_K_1_null_svertka[id_2_versh, 0] -
np.full((1, len(id_2_versh[0])), centers[j, 1])) ** 2) ** 0.5
num_center_of_sharp = np.argmin(delt_kriv[id_2_versh[0], :], axis=1).T
massiv_face_klast[id[id_2_versh], 0] = num_center_of_sharp.T
curvature_face_klast[id[id_2_versh], 0] = f_K_1_null_svertka[id_2_versh, 0]
curvature_face_klast[id[id_2_versh], 1] = f_K_2_null_svertka[id_2_versh, 0]
# 2 случай, 1 острые вершины
if (len(id_1_versh[0]) > 0):
f_K_1_null_svertka[id_1_versh, 0] = np.sum(f_K_1_null3[id_1_versh[0], :], axis=1)
f_K_2_null_svertka[id_1_versh, 0] = np.sum(f_K_2_null3[id_1_versh[0], :], axis=1)
for j in range(centers.shape[0]):
delt_kriv[id_1_versh, j] = ((f_K_1_null_svertka[id_1_versh, 0] -
np.full((1, len(id_1_versh[0])), centers[j, 0])) ** 2 +
(f_K_1_null_svertka[id_1_versh, 0] -
np.full((1, len(id_1_versh[0])), centers[j, 1])) ** 2) ** 0.5
num_center_of_sharp = np.argmin(delt_kriv[id_1_versh[0], :], axis=1).T
massiv_face_klast[id[id_1_versh], 0] = num_center_of_sharp.T
curvature_face_klast[id[id_1_versh], 0] = f_K_1_null_svertka[id_1_versh, 0]
curvature_face_klast[id[id_1_versh], 1] = f_K_2_null_svertka[id_1_versh, 0]
# 3 случай, 0 острые вершины
if (len(id_0_versh[0]) > 0):
f_K_1_null_svertka[id_0_versh, 0] = np.sum(f_K_1_null3[id_0_versh[0], :], axis=1)
f_K_2_null_svertka[id_0_versh, 0] = np.sum(f_K_2_null3[id_0_versh[0], :], axis=1)
for j in range(centers.shape[0]):
delt_kriv[id_0_versh, j] = ((f_K_1_null_svertka[id_0_versh, 0] -
np.full((1, len(id_0_versh[0])), centers[j, 0])) ** 2 +
(f_K_1_null_svertka[id_0_versh, 0] -
np.full((1, len(id_0_versh[0])), centers[j, 1])) ** 2) ** 0.5
num_center_of_sharp = np.argmin(delt_kriv[id_0_versh[0], :], axis=1).T
massiv_face_klast[id[id_0_versh], 0] = num_center_of_sharp.T
curvature_face_klast[id[id_0_versh], 0] = f_K_1_null_svertka[id_0_versh, 0]
curvature_face_klast[id[id_0_versh], 1] = f_K_2_null_svertka[id_0_versh, 0]
# Вывод решения
return idx_K, centers, massiv_face_klast, curvature_face_klast, curvature_meanРезультат кластеризации приведен на рисунке 6.

Этап предварительной сегментации выполняется с помощью единственного метода класса Pre_segmentation_faces.
def func_calculate_pre_segmentation(self):
# Функция предварительной сегментации slt и визуализации решения
name_safe = sff.name_of_results(self.pl_sphere_cyl) + '_stage_3'
save_dict={} #словарь для сохранения списков с вложенными массивами
if self.pl_zagr[3] == 1:
curveTolerance, angleTolerance = sff.tolerances_for_segmentation(self.pl_sphere_cyl, self.mesh)
massiv_face_klast_all=copy.deepcopy(self.massiv_face_klast)
faces_all = copy.deepcopy(self.mesh.faces)
normals_all = copy.deepcopy(self.mesh.normals)
curvature_face_klast_all = copy.deepcopy(self.curvature_face_klast)
ko = 1 # Запись для цвета
i = -1
struct_seg=np.array([])
surface_seg=[]
surfaceNormal_seg=[]
surfaceCurve_seg = []
area_segments=np.array([])
num_segments=np.array([])
color_segments=np.array([])
curve_of_segments1 = np.array([])
# 3.1 Основной цикл сегментирования данных по значению кривизны
t=()
for j in range(self.centers.shape[0]):
# Центральная точка
if (np.size(massiv_face_klast_all)>0):
id = np.where((massiv_face_klast_all[:, 0]) == j)
length_of_num_segments=len(id[0])
while (length_of_num_segments>0):
i += 1
#Подход случайного выбора
if (1==0):
msize = len(id[0])
idx = np.random.permutation(msize)
firstpart = id[0][idx[0]]
else:
#Подход близости к центру кластера (центральному зерну)
array_for_first=((curvature_face_klast_all[id, 0]-
np.full((len(id[0]),1),self.centers[j, 0])) ** 2 +
(curvature_face_klast_all[id, 1] -
np.full((len(id[0]), 1),self.centers[j, 1])) ** 2) **(0.5)
min_idx = np.argmin(array_for_first)
firstpart=id[0][min_idx]
targetPoint = self.mesh.vertices[faces_all[firstpart, 0],:]
targetVector = curvature_face_klast_all[firstpart,:]
targetVector2 = normals_all[firstpart,:]
if (abs(curvature_face_klast_all[firstpart, 0]) > 0.005) or \
((abs(curvature_face_klast_all[firstpart, 1]) > 0.005)):
surface, surfaceNormal,surfaceCurve = sff.ExtractSurface_by_curve_2020_2_curves(
self.mesh.vertices, faces_all,
normals_all, curvature_face_klast_all,
targetPoint, targetVector, curveTolerance,0
)
else:
surface, surfaceNormal, surfaceCurve = sff.ExtractSurface_by_curve_2020_2_curves_norm(
self.mesh.vertices, faces_all,
normals_all, curvature_face_klast_all,
targetPoint, targetVector, curveTolerance,
targetVector2,angleTolerance,0
)
if (surface.size==0):
surface, surfaceNormal, surfaceCurve = sff.ExtractSurface_by_curve_2020_2_curves(
self.mesh.vertices, faces_all,
normals_all, curvature_face_klast_all,
targetPoint, targetVector, curveTolerance, 0
)
# Исключение сегментированных значений из общего массива
massiv_face_klast_all, faces_all, \
normals_all, curvature_face_klast_all=sff.facet_exception(
massiv_face_klast_all, faces_all, normals_all,
curvature_face_klast_all, surface
)
if massiv_face_klast_all.shape[0]>0:
id=np.where((massiv_face_klast_all[:, 0]) == j)
length_of_num_segments = len(id[0])
else:
id=()
length_of_num_segments = len(id)
# Сохранение структуры сегментированных кусков
surface_seg.append([])
surface_seg[i].append(surface)
surfaceNormal_seg.append([])
surfaceNormal_seg[i].append(surfaceNormal)
surfaceCurve_seg.append([])
surfaceCurve_seg[i].append(surfaceCurve)
#Сохранение в словарь
save_dict['surface_seg' + str(i)] = surface_seg[i]
save_dict['surfaceNormal_seg' + str(i)] = surfaceNormal_seg[i]
save_dict['surfaceCurve_seg' + str(i)] = surfaceCurve_seg[i]
#Вычисление площадей
area=sff.stl_Area_segment(self.mesh.vertices.T,surface.T)
area_segments = np.append(area_segments, area)
# Количество фасет в сегменте
num_segments = np.append(num_segments, surface.shape[0])
# Порядковый номер для цвета сегмента
color_segments=np.append(color_segments, ko)
# Кривизна сегмента
curve_of_segments1=np.append(curve_of_segments1, targetVector)
ko=ko+1
print('Осталось фасет фактически: '+ str(massiv_face_klast_all.shape[0])+
'; распознано: '+str(np.sum(num_segments))+'; осталось фасет расчетно:'+
str(self.mesh.faces.shape[0]-np.sum(num_segments)))
if ko > 1:
struct_seg1 = num_segments.shape[0]
curve_of_segments = np.zeros([num_segments.shape[0],2])
for numerate in range(num_segments.shape[0]):
curve_of_segments[numerate,:] = curve_of_segments1[0+numerate*2:1+numerate*2]
else:
struct_seg1 = 0
curve_of_segments=np.array([])
struct_seg=np.append(struct_seg, struct_seg1)На рисунке 7 приведены результаты четвертого этапа алгоритма.
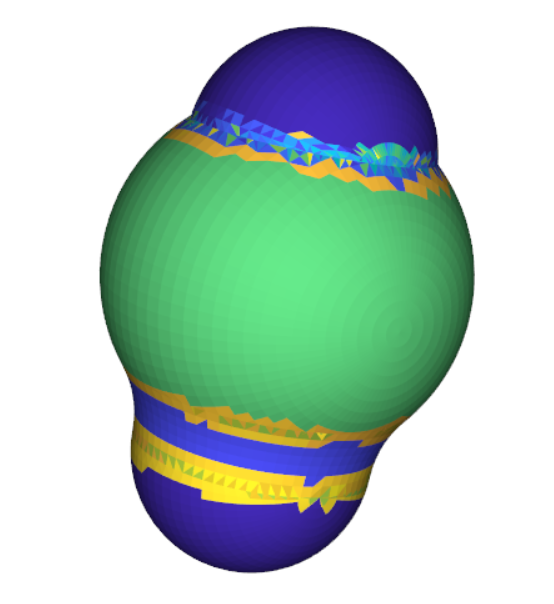
В результате предварительной сегментации остается много неверно сегментированных фасет на границах основных поверхностей. Уменьшить их количество позволяет этап окончательной сегментации, для которого был создан класс Final_segmentation_faces.
class Final_segmentation_faces():
"""Класс расчета структуры предварительной сегментации фасет"""
def __init__(self,stl_pre_segment,mesh):
self.pre = stl_pre_segment
self.mesh = mesh
def func_calculate_final_segmentation(self):
# Функция окончательной сегментации slt и визуализации решения
name_safe = sff.name_of_results(self.pre.pl_sphere_cyl) + '_stage_4'
save_dict = {} # словарь для сохранения списков с вложенными массивами
if self.pre.pl_zagr[4] == 1:
mesh_pre = copy.deepcopy(self.pre.mesh)
curveTolerance, angleTolerance = sff.tolerances_for_segmentation(self.pre.pl_sphere_cyl, mesh_pre)
# Критерий максимальной площади
# Общая площадь всех сегментов
Area_of_segments_total = sff.stl_Area_segment(mesh_pre.vertices.T, mesh_pre.faces.T)
nm = np.round(self.pre.massiv_face_klast.shape[0] / mesh_pre.struct_seg[0] * 0.2)
eps = 1E-5
Toleranse_area = Area_of_segments_total / self.pre.massiv_face_klast.shape[0] * nm
Tolerance_of_curve_in_merging = curveTolerance
# Общий периметр
faces_perimetr, deameter_max = sff.perimeter_and_diametr_calculation(mesh_pre.vertices, mesh_pre.faces)
# Создание матрицы координат вершин сетки, последняя точка - удаленная от сетки
vertices1=np.zeros([mesh_pre.vertices.shape[0]+1,3])
vertices1=np.vstack((mesh_pre.vertices, np.array([np.mean(mesh_pre.vertices,axis=0) + deameter_max * 1E+3])))
# Находится максимальный элемент
struct_seg1=copy.deepcopy(mesh_pre.struct_seg)
area_segments1 = copy.deepcopy(mesh_pre.area_segments)
num_segm_counter=copy.deepcopy(mesh_pre.struct_seg[0])
while (num_segm_counter>1):
max_index_Area = np.argmax(area_segments1)
surface_search = copy.deepcopy(mesh_pre.surface_seg[max_index_Area])
counter = 1
while (counter == 1):
counter = 0
num_cor=np.arange(mesh_pre.struct_seg[0])
num_cor=np.delete(num_cor, num_cor[max_index_Area])
print(str(num_segm_counter))
for idx_of_segm in range(mesh_pre.struct_seg[0] - 1):
# Поиск общей границы
if (area_segments1[0,num_cor[idx_of_segm]] > 0):
surface_search2=copy.deepcopy(mesh_pre.surface_seg[num_cor[idx_of_segm]])
surface_search2_uniq =np.unique(np.vstack((np.array([surface_search2[:, 0]]),
np.array([surface_search2[:, 1]]),
np.array([surface_search2[:, 2]]))),
return_index=False, return_inverse=False,
return_counts=False, axis=None)
surface_search1_uniq = np.unique(np.vstack((np.array([surface_search[:, 0]]),
np.array([surface_search[:, 1]]),
np.array([surface_search[:, 2]]))),
return_index=False, return_inverse=False,
return_counts=False, axis=None)
F_massiv_boundary = np.intersect1d(surface_search1_uniq, surface_search2_uniq)
if (F_massiv_boundary.shape[0]) > 2:
# средние кривизны границы
c_mean_boundaru = np.array([np.mean(self.pre.curvature_face_klast[F_massiv_boundary,0]),
np.mean(self.pre.curvature_face_klast[F_massiv_boundary, 1])])
# Расстояние
DC=np.abs(((mesh_pre.curve_of_segments[max_index_Area,0]-c_mean_boundaru[0])**2+
(mesh_pre.curve_of_segments[max_index_Area,1]-c_mean_boundaru[1])**2)**0.5-
((mesh_pre.curve_of_segments[num_cor[idx_of_segm],0]-c_mean_boundaru[0])**2+
(mesh_pre.curve_of_segments[num_cor[idx_of_segm],1]-c_mean_boundaru[1])**2)**0.5)
if ((area_segments1[0, num_cor[idx_of_segm]] < Toleranse_area) or
(area_segments1[0, max_index_Area] < Toleranse_area)) or \
((area_segments1[0, num_cor[idx_of_segm]] < Toleranse_area) and
(area_segments1[0, max_index_Area] < Toleranse_area)):
D = DC * eps
else:
D = copy.deepcopy(DC)
# Поиск периметров сегментов и общей границы
# 2. Делаем ответные области фасету (из общей вычитаем текущие)
f_surface_search_sympathetic, \
f_surface_search_sympathetic1= copy.deepcopy(mesh_pre.faces), \
copy.deepcopy(mesh_pre.faces)
f_surface_search_sympathetic = sff.facet_exception_lite(f_surface_search_sympathetic,
surface_search)
f_surface_search_sympathetic1 = sff.facet_exception_lite(f_surface_search_sympathetic1,
surface_search2)
# 3. Поиск пересекающихся вершин с общей структурой, т.е. границ
boundary_surface_poisk = sff.boundary_intersection(surface_search,
f_surface_search_sympathetic)
boundary_surface_poisk1 = sff.boundary_intersection(surface_search2,
f_surface_search_sympathetic)
# 4. Матрицы с v1(end+1,:) вершиной
surface_search_boundary = np.full((surface_search.shape[0], 3), vertices1.shape[0]-1)
surface_search_boundary1 = np.full((surface_search2.shape[0], 3), vertices1.shape[0]-1)
surface_search_boundary_common = np.full((surface_search2.shape[0], 3), vertices1.shape[0]-1)
# 5. Включение в матрицы вершины не 0
# Большая область
surface_search_boundary = sff.filling_in_common_vertices(surface_search_boundary,
surface_search,
boundary_surface_poisk)
surface_search_boundary1 = sff.filling_in_common_vertices(surface_search_boundary1,
surface_search2,
boundary_surface_poisk1)
surface_search_boundary_common = sff.filling_in_common_vertices(surface_search_boundary_common,
surface_search2,
F_massiv_boundary)
# 6. Матрицы расстояний в массиве vertices1
P_surface_search_boundary_matrix = sff.search_matrix_compilation(vertices1,
surface_search_boundary)
P_surface_search_boundary_matrix1 = sff.search_matrix_compilation(vertices1,
surface_search_boundary1)
P_surface_search_boundary_matrix_common = sff.search_matrix_compilation(vertices1,
surface_search_boundary_common)
# 7. Обнуление ненужных расстояний и
# поиск периметров
idx = np.where(P_surface_search_boundary_matrix[:,0] > deameter_max)
P_surface_search_boundary_matrix[idx,0] = 0
P_surface_search= np.sum(P_surface_search_boundary_matrix)
idx = np.where(P_surface_search_boundary_matrix1[:,0] > deameter_max)
P_surface_search_boundary_matrix1[idx, 0] = 0
P_surface_search1 = np.sum(P_surface_search_boundary_matrix1)
idx = np.where(P_surface_search_boundary_matrix_common[:,0] > deameter_max)
P_surface_search_boundary_matrix_common[idx, 0] = 0
P_boundary = np.sum(P_surface_search_boundary_matrix_common)
if P_boundary>0:
D *= np.min([P_surface_search, P_surface_search1]) / P_boundary
else:
D *= np.min([P_surface_search, P_surface_search1])
if abs(mesh_pre.curve_of_segments[max_index_Area,0]) < 0.005 or \
abs(mesh_pre.curve_of_segments[max_index_Area,1]) < 0.005:
#Массивы границ
if (idx_of_segm==109):
g=0
array_boundary=sff.creating_an_array_of_borders(surface_search,F_massiv_boundary)
norm_boundary=copy.deepcopy(mesh_pre.surfaceNormal_seg[max_index_Area][array_boundary,:])
array_boundary1 = sff.creating_an_array_of_borders(surface_search2, F_massiv_boundary)
norm_boundary_symp = copy.deepcopy(mesh_pre.surfaceNormal_seg[num_cor[idx_of_segm]][array_boundary1,:])
norm_boundary1=np.zeros([1,3])
norm_boundary_symp1 = np.zeros([1, 3])
if len(array_boundary) > 1:
for i in range(3):
norm_boundary1[0,i] = np.mean(norm_boundary[:,i])
else:
norm_boundary1=copy.deepcopy(norm_boundary)
if len(array_boundary1) > 1:
for i in range(3):
norm_boundary_symp1[0,i] = np.mean(norm_boundary_symp[:,i])
else:
norm_boundary_symp1 = copy.deepcopy(norm_boundary_symp)
angles2 = np.arccos(np.sum((norm_boundary1* np.full((norm_boundary1.shape[0],3),
norm_boundary_symp1)),axis=1))/np.pi*180
if (angles2 > angleTolerance):
D = Tolerance_of_curve_in_merging * 2
# Объединение в случае удовлетворения условиям
if (D < Tolerance_of_curve_in_merging):
# Поглощение сегмента
surface_search = np.vstack((surface_search, surface_search2))
mesh_pre.surface_seg[max_index_Area] = copy.deepcopy(surface_search)
# Обнуление структуры поглощенного сегмента
struct_seg1 -= 1
# Структура фасет поверхности
#del mesh_pre.surface_seg[num_cor[idx_of_segm]]
mesh_pre.surface_seg[num_cor[idx_of_segm]] = np.array([])
# Нормали фасет поверхности
normal_search = np.vstack((mesh_pre.surfaceNormal_seg[max_index_Area],
mesh_pre.surfaceNormal_seg[num_cor[idx_of_segm]]))
mesh_pre.surfaceNormal_seg[max_index_Area] = copy.deepcopy(normal_search)
#np.append(mesh_pre.surfaceNormal_seg[max_index_Area],
# mesh_pre.surfaceNormal_seg[num_cor[idx_of_segm]])
mesh_pre.surfaceNormal_seg[num_cor[idx_of_segm]] = np.array([])
# Кривизны фасет поверхностей
curve_search = np.vstack((mesh_pre.surfaceCurve_seg[max_index_Area],
mesh_pre.surfaceCurve_seg[num_cor[idx_of_segm]]))
mesh_pre.surfaceCurve_seg[max_index_Area] = copy.deepcopy(curve_search)
#np.append(mesh_pre.surfaceCurve_seg[max_index_Area],
# mesh_pre.surfaceCurve_seg[num_cor[idx_of_segm]])
mesh_pre.surfaceCurve_seg[num_cor[idx_of_segm]] = np.array([])
# Площадь поверхности
area_segments1[0,num_cor[idx_of_segm]] = 0
# Количество элементов в сегменте
mesh_pre.num_segments[max_index_Area] += mesh_pre.num_segments[num_cor[idx_of_segm]]
mesh_pre.num_segments[num_cor[idx_of_segm]] = 0
# Цвет сегмента убираем
mesh_pre.color_segments[0,num_cor[idx_of_segm]] = 0
# Кривизна сегмента
mesh_pre.curve_of_segments[num_cor[idx_of_segm], 0] = 0
mesh_pre.curve_of_segments[num_cor[idx_of_segm], 1] = 0
num_cor[idx_of_segm]=-1
num_segm_counter -= 1
if counter==0:
counter = 1
else:
pass
area_segments1[0,max_index_Area] = 0
num_segm_counter -= 1
# Сохраниние структуры данных
struct_seg=np.array([])
surface_seg=[]
surfaceNormal_seg=[]
surfaceCurve_seg = []
area_segments=np.array([])
num_segments=np.array([])
color_segments=np.array([])
curve_of_segments = np.array([])
idx = np.where(mesh_pre.num_segments[:] > 0)
if len(idx[0]) > 0:
for j in range(len(idx[0])):
surface_seg.append([])
surface = mesh_pre.surface_seg[idx[0][j]]
surface_seg[j] = copy.deepcopy(surface)
surfaceNormal_seg.append([])
surfaceNormal = mesh_pre.surfaceNormal_seg[idx[0][j]]
surfaceNormal_seg[j] = copy.deepcopy(surfaceNormal)
surfaceCurve_seg.append([])
surfaceCurve = mesh_pre.surfaceCurve_seg[idx[0][j]]
surfaceCurve_seg[j] = copy.deepcopy(surfaceCurve)
#Вычисление площадей
area=sff.stl_Area_segment(mesh_pre.vertices.T,surface.T)
area_segments = np.append(area_segments, area)
# Количество фасет в сегменте
num_segments = np.append(num_segments, mesh_pre.num_segments[idx[0][j]])
# Порядковый номер для цвета сегмента
color_segments = np.append(color_segments, j+1)
# Кривизна сегмента
curve_of_segments = np.append(curve_of_segments, mesh_pre.curve_of_segments[idx[0][j]])
# Сохранение в словарь
save_dict['surface_seg' + str(j)] = surface_seg[j]
save_dict['surfaceNormal_seg' + str(j)] = surfaceNormal_seg[j]
save_dict['surfaceCurve_seg' + str(j)] = surfaceCurve_seg[j]
struct_seg1=num_segments.shape[0]
save_dict['area_segments'] = area_segments
save_dict['num_segments'] = num_segments
save_dict['curve_of_segments'] = curve_of_segments
save_dict['color_segments'] = color_segments
save_dict['struct_seg'] = struct_seg1
scipy.io.savemat(self.pre.path_file + name_safe + '.mat', save_dict)
struct_seg=np.append(struct_seg, struct_seg1)Итог работы алгоритма приведен на рисунке 8.
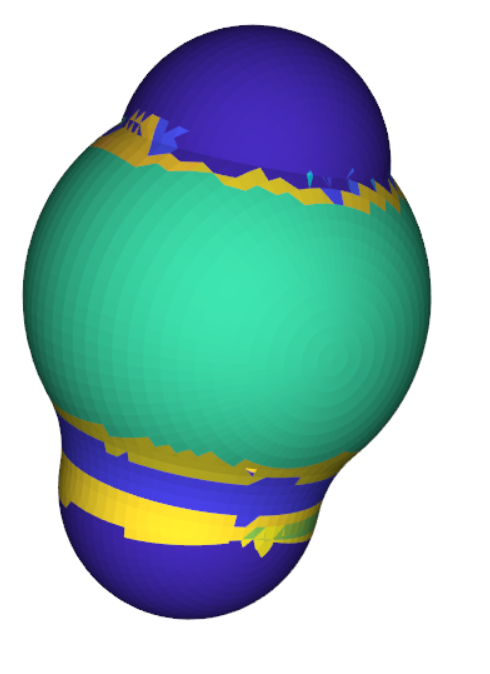
В результате все же остаются неверно сегментированные фасеты на стыках граней, особенно их много при нерезком изменении кривизны. В алгоритме настраиваются начальное количество кластеров, допуски на угол и на отклонение нормали. Все они влияют на получаемый результат.
Для ускорения работы алгоритма на больших «боевых» сетках требуется добавить многопоточность в код, что планирую сделать в будущем.
Ссылки
Роджерс, Д. Математические основы машинной графики / Д. Роджерс, Дж. Адамс. – Москва : Мир, 2001. – 604 c.
Cohen-Steiner, D. Restricted Delaunay triangulations and normal cycle / D. Cohen-Steiner, J. Morvan // 19th Annu. ACM Sympos. Comput. Geom. – 2003. – P. 312-321.
Discrete Differential-Geometry Operators for Triangulated 2-Manifolds / M. Meyer, M. Desbrun, P. Schröder, H. Barr // International Workshop on Visualization and Mathematics, Berlin, Germany. – 2002. – P.35-37.
Taubin, G. Estimating the Tensor of Curvature of a Surface from a Polyhedral Approximation / G. Taubin // Fifth International Conference on Computer Vision. – 1995. – P. 902-907.
Вандер Плас Дж. Python для сложных задач. Наука о данных и машинное обучение / Плас Дж. Вандер. – Санкт-Петербург : Питер, 2018. – 516 c.
Guillaume, L. A new curvature tensor based segmentation method for optimized triangulated CAD / L. Guillaume, D. Florent, Baskurt Atilla // Comput. Aided Des. – 2005. – Vol. 37. – P. 975-987.
Schettini, R. A Segmentation Algorithm For Color Images / R. Schettini // Pattern Recognition Letters. – 1993. – Vol. 14. – P. 499-506.

