XGBoost и другие методы на основе дерева решений, обучающие модели при помощи градиентного подъема, принимают решение через сравнение, тогда как определить оператор сравнения категорий математически — это нетривиальная задача.
Ниже объясняется, какие есть варианты, подробно рассказывается об их плюсах и минусах. Особое внимание уделяется встроенной поддержке категориальных функций, представленных недавно в XGBoost и LightGBM.
Если вас интересует градиентный бустинг и его применение к дереву решений, посмотрите мою книгу.
Деревья решений
Деревья решений основываются на сравнении, как показано ниже:

Простое дерево решений
Если ввод — это строка данных с двумя столбцами A=21 и B=111, то выходным значением станет вес 4.
Ограничение этого типа дерева решений состоит в том, что признаками могут быть только числа.
Стандартные способы обработки категориальных признаков
Прямое кодирование
Один из распространенных способов обработки категориальных значений — прямое кодирование: чтобы преобразовать нечисловые категориальные значения в числовые, под каждую возможную категорию выделяется столбец.
Когда категория применяется к текущей строке набора данных, соответствующие столбцы устанавливаются равными 1, а в противном случае — 0.
Фрагмент кода ниже показывает стандартное прямое кодирование в Pandas:
import pandas as pd
dtf = pd.DataFrame({'cat': ['one', 'two', 'three', 'one', 'one', 'three'],
'num': [1, 2, 3, 4, 5, 6]})
print(pd.get_dummies(dtf))
#> num cat_one cat_three cat_two
#> 0 1 1 0 0
#> 1 2 0 0 1
#> 2 3 0 1 0
#> 3 4 1 0 0
#> 4 5 1 0 0
#> 5 6 0 1 0Одно из основных ограничений прямого кодирования — то, что столбцов в наборе данных окажется столько, сколько в наборе отдельных категорий.
Важно отметить, что в обучающем и тренировочном наборах данных у вас должны быть одни и те же уникальные значения, иначе во время прогнозирования некоторые столбцы просто не будут учтены.
GLMM
GLMM (обобщенная линейная смешанная модель) преобразует нечисловые категории в числа при помощи обобщенной линейной смешанной модели.
generalized (обобщенная) означает, что это просто обобщение линейных моделей, где целевая переменная может быть преобразована функцией, подобной логарифму. А значит, на одной и той же математической базе можно смоделировать стандартную линейную и логистическую регрессии.
mixed (смешанная) указывает, что модели могут объединять постоянные и случайные эффекты, то есть среднее значение прогнозируемой переменной во множестве наблюдений предпочтительно постоянное или случайное.
Для категориального кодирования GLMM фиксирует случайный эффект каждой категории, которая соответствует модели такого типа:
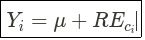
Смешанная модель прогнозирует Y для категории I. Формула автора.
Yi — это значение, спрогнозированное моделью Mixel для цели Y и категории i; μ — глобальное среднее значение Y и постоянный эффект, а REci — случайный эффект, возникающий из-за категории i.
Это означает, что REci фиксирует эффект категории, и это закодированное значение категории.
Вся эта теория сводится в несколько строк кода:
import pandas as pd
import category_encoders as ce
dtf = pd.DataFrame({'cat': ['one', 'two', 'three', 'one', 'one', 'three'],
'num': [1, 2, 3, 4, 5, 6],
'to_predict': [1.2, 2.3, 3.6, 4.1, 5.2, 6.6]})
targeted = ce.glmm.GLMMEncoder(cols='cat',
return_df=True).fit_transform(
dtf['cat'],
dtf['to_predict'])
print(targeted)
#> cat
#> 0 -0.040995
#> 1 -0.069332
#> 2 0.110327
#> 3 -0.040995
#> 4 -0.040995
#> 5 0.110327Если вам это интересно, вот важная строка categorical_encoders:
# This one line is the crucial one in the category_encoders library
md = smf.mixedlm('target ~ 1', data, groups=data['feature']).fit()Эта строка тренирует модель, которая описывается формулой выше.
Нативная поддержка XGBoost
Как показано выше, свойства категориальных значений можно изменить, либо преобразовав их в реальные значения (это подход GLMM), либо изменив структуру набора данных и добавив столбец для каждой возможной категории (это подход прямого кодирования).
Но это не лучший способ интегрировать поддержку категорий в стандартную структуру градиентного бустинга: дерева решений.
Включение вместо сравнения
Естественной кажется замена сравнения включением. То есть вместо того, чтобы проверять, больше или меньше заданного порога некоторое значение, можно проверить включение значения в заданный набор категорий. Заменить

на

Это можно сделать, написав метод создания функции условия для узла дерева так, чтобы вместо сравнения (как в моей предыдущей статье) он поддерживал включение:
def _create_condition(self, col_name, split_value):
"""
Create a closure that capture split value
"""
if isinstance(split_value, (int, float)):
return lambda dta : dta[col_name] < split_value
else:
return lambda dta : dta[col_name].isin(split_value) if isinstance(dta[col_name], pd.Series) else dta[col_name] in split_valueГенерация возможных списков категорий
В стандартном методе, который в качестве условия разделения берет значение, возможные разделения генерируются путем упорядочения значений в рассматриваемом столбце и сохранения уникальных значений.
По этому значению разделения вычисляется усиление для результатов разбиения — левого и правого узлов. При работе с категориями порядок уже не имеет значения, а условия-кандидаты на разбиение — это не одно значение, а список категорий.
При этом ничего не известно о том, как лучше всего перегруппировать категории в множества, чтобы оптимизировать выигрыш, один из вариантов — сгенерировать все возможные комбинации категорий.
Вот код, который создает разбиение по порогу для числовых значений в _numerical_split; для генерации возможных комбинаций вводим новый метод _categorical_split:
def _numerical_split(self, col_name, x_sorted):
""" Create splitting candidates using threshold
"""
masks = []
split_values = []
prev_value = None
for split_idx in range(1, x_sorted.shape[0]):
if prev_value and x_sorted[col_name].iloc[split_idx] == prev_value:
continue
# skip this index if the spliting value is the same as before
prev_value = x_sorted[col_name].iloc[split_idx]
split_values.append(prev_value)
masks.append(x_sorted[col_name] < prev_value)
return masks, split_values
def _categorical_split(self, col_name, x_sorted):
""" Create splitting candidates using inclusion list of categories
"""
masks = []
groups = []
categories = list(x_sorted[col_name].unique())
for n in range(1, len(categories)):
for group in combinations(categories, n):
masks.append(x_sorted[col_name].isin(group))
groups.append(group)
return masks, groupsМаски Pandas — очень удобный способ обрабатывать оба случая одним и тем же подходом.
Собираем все воедино
Вот полная реализация градиентного бустинга деревьев решений с поддержкой числовых и категориальных данных:
from itertools import combinations
from collections import OrderedDict as OD
import matplotlib.pyplot as plt
import pandas as pd
from jax import grad, jacfwd, jacrev, jit
import jax.numpy as jnp
import numpy as np
import random
def hessian(fun):
return jit(jacfwd(jacrev(fun)))
class DecisionNode:
"""
Node decision class.
This is a simple binary node, with potentially two childs: left and right
Left node is returned when condition is true
False node is returned when condition is false<
"""
def __init__(self, name, condition, value=None):
self.name = name
self.condition = condition
self.value = value
self.left = None
self.right = None
def add_left_node(self, left):
self.left = left
def add_right_node(self, right):
self.right = right
def is_leaf(self):
"""
Node is a leaf if it has no child
"""
return (not self.left) and (not self.right)
def next(self, data):
"""
Return next code depending on data and node condition
"""
cond = self.condition(data)
if cond:
return self.left
else:
return self.right
class DecisionTree:
"""
A DecisionTree is a model that provides predictions depending on input.
Prediction is the sum of the values attached to leaf activated by input
"""
def __init__(self, objective, nb_estimators, max_depth):
"""
A DecisionTree is defined by an objective, a number of estimators and a max depth.
"""
self.roots = [DecisionNode(f'root_{esti}', None, 0.0) for esti in range(0, nb_estimators)]
self.objective = objective
self.lbda = 0.0
self.gamma = 1.0 * 0
self.grad = grad(self.objective)
self.hessian = hessian(self.objective)
self.max_depth = max_depth
self.base_score = None
self.label = 'root'
def _create_condition(self, col_name, split_value):
"""
Create a closure that capture split value
"""
if isinstance(split_value, (int, float)):
return lambda dta : dta[col_name] < split_value
else:
return lambda dta : dta[col_name].isin(split_value) if isinstance(dta[col_name], pd.Series) else dta[col_name] in split_value
def _pick_columns(self, columns):
return random.choice(columns)
def _add_child_nodes(self, node, nodes,
node_x, node_y,
split_value, split_column,
nb_nodes,
left_w, right_w, prev_w):
node.name = f'{split_column} < {split_value}'
node.condition = self._create_condition(split_column, split_value) # we must create a closure to capture split_value copy
node.add_left_node(DecisionNode(f'left_{nb_nodes} - {split_column} < {split_value}',
None, left_w + prev_w))
node.add_right_node(DecisionNode(f'right_{nb_nodes} - {split_column} >= {split_value}',
None, right_w + prev_w))
if isinstance(split_value, (int, float)):
mask = node_x[split_column] < split_value
else:
if isinstance(node_x[split_column], pd.Series):
mask = node_x[split_column].isin(split_value)
else:
mask = node_x[split_column] in split_value
# Reverse order to ensure bfs
nodes.append((node.left,
node_x[mask].copy(),
node_y[mask].copy(),
left_w + prev_w))
nodes.append((node.right,
node_x[~mask].copy(),
node_y[~mask].copy(),
right_w + prev_w))
def fit(self, x_train, y_train):
"""
Fit decision trees using x_train and objective
"""
self.base_score = y_train.mean()
for tree_idx, tree_root in enumerate(self.roots):
# store current node (currenly a lead), x_train and node leaf weight
nodes = [(tree_root, x_train.copy(), y_train.copy(), 0.0)]
nb_nodes = 0
# Add node to tree using bfs
while nodes:
node, node_x, node_y, prev_w = nodes.pop(0)
node_x['pred'] = self.predict(node_x)
split_column = self._pick_columns(list(x_train.columns)) # XGBoost use a smarter heuristic here
split_found, split_value, left_w, right_w = self._find_best_split(split_column,
node_x, node_y)
if split_found:
self._add_child_nodes(node, nodes,
node_x, node_y,
split_value, split_column,
nb_nodes,
left_w, right_w, prev_w)
nb_nodes += 1
if nb_nodes >= 2**self.max_depth-1:
break
def _gain_and_weight(self, x_train, y_train):
"""
Compute gain and leaf weight using automatic differentiation
"""
pred = x_train['pred'].values
G_i = self.grad(pred, y_train.values).sum()
H_i = self.hessian(pred, y_train.values).sum()
return -0.5 * G_i * G_i / (H_i + self.lbda) + self.gamma, -G_i / (H_i + self.lbda)
def _numerical_split(self, col_name, x_sorted):
masks = []
split_values = []
prev_value = None
for split_idx in range(1, x_sorted.shape[0]):
if prev_value and x_sorted[col_name].iloc[split_idx] == prev_value:
continue
# skip this index if the spliting value is the same as before
prev_value = x_sorted[col_name].iloc[split_idx]
split_values.append(prev_value)
masks.append(x_sorted[col_name] < prev_value)
return masks, split_values
def _categorical_split(self, col_name, x_sorted):
masks = []
groups = []
categories = list(x_sorted[col_name].unique())
for n in range(1, len(categories)):
for group in combinations(categories, n):
masks.append(x_sorted[col_name].isin(group))
groups.append(group)
return masks, groups
def _find_best_split(self, col_name, node_x, node_y):
"""
Compute best split
"""
x_sorted = node_x.sort_values(by=col_name)
y_sorted = node_y[x_sorted.index]
current_gain, _ = self._gain_and_weight(x_sorted, node_y)
gain = 0.0
split_found = False
split_value, best_left_w, best_right_w = None, None, None
if x_sorted[col_name].dtype == 'category':
masks, values = self._categorical_split(col_name, x_sorted)
else:
masks, values = self._numerical_split(col_name, x_sorted)
for mask, split_candidate in zip(masks, values):
left_data = x_sorted[mask]
right_data = x_sorted[~mask]
left_y = y_sorted[mask]
right_y = y_sorted[~mask]
left_gain, left_w = self._gain_and_weight(left_data, left_y)
right_gain, right_w = self._gain_and_weight(right_data, right_y)
if current_gain - (left_gain + right_gain) > gain:
gain = current_gain - (left_gain + right_gain)
split_found = left_data.shape[0]
split_value = split_candidate
best_left_w = left_w
best_right_w = right_w
return split_found, split_value, best_left_w, best_right_w
def predict(self, data):
preds = []
for _, row in data.iterrows():
pred = 0.0
for tree_idx, root in enumerate(self.roots):
child = root
while child and not child.is_leaf():
child = child.next(row)
pred += child.value
preds.append(pred)
return np.array(preds) + self.base_score
def show(self):
print('not yet implemented')
def squared_error(y_pred, y_true):
diff = y_true - y_pred
return jnp.dot(diff, diff.T)
x_train = pd.DataFrame({"A" : [3.0, 2.0, 1.0, 4.0, 5.0, 6.0, 7.0]})
y_train = pd.DataFrame({"Y" : [3.0, 2.0, 1.0, 4.0, 5.0, 6.0, 7.0]})
x_train['A'] = x_train['A'].astype('category')
tree = DecisionTree(squared_error, 1, 3)
tree.fit(x_train, y_train['Y'])
pred = tree.predict(pd.DataFrame({'A': [1., 2., 3., 4., 5., 6., 7.]}))
print(pred) #-> [1. 2. 3. 4. 5. 6. 7.]
tree = DecisionTree(squared_error, 2, 3)
tree.fit(x_train, y_train['Y'])
pred = tree.predict(pd.DataFrame({'A': [1., 2., 3., 4., 5., 6., 7.]}))
print(pred) #-> [1. 2. 3. 4. 5. 6. 7.]
tree = DecisionTree(squared_error, 4, 2)
tree.fit(x_train, y_train['Y'])
pred = tree.predict(pd.DataFrame({'A': [1., 2., 3., 4., 5., 6., 7.]}))
print(pred) # -> [1. 2. 3. 4. 5. 5.9999995 7. ]
x_train = pd.DataFrame({'A': [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0,
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0,],
'B': [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,]})
y_train = pd.DataFrame({"Y" : [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0,
1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5]})
x_train['A'] = x_train['A'].astype('category')
tree = DecisionTree(squared_error, 1, 6)
tree.fit(x_train, y_train['Y'])
pred = tree.predict(pd.DataFrame({'A': [1., 2., 3., 4., 5., 6., 7.],
'B': [0., 1., 0., 1., 0., 1., 0.]}))
print(pred) #-> [1. 2.5 3. 4.5 5. 6.5 7. ]В приведенном простом примере применение категориального или числового разбиения дает те же результаты. В случае с категориями код просто медленнее, здесь важно количество исследуемых комбинаций:
from itertools import combinations
categories = [1, 2, 3, 4, 5, 6, 7]
count = 0
for n in range(1, len(categories)):
for group in combinations(categories, n):
count += 1
print('Explore', count, 'combinations')
# Explore 126 combinationsЧтобы различать числовые и категориальные данные, используется внутренний код category в Pandas.
Проблемы с производительностью
Реализация работает в соответствии с ожиданиями и поддерживает категориальные значения, но исследуются все возможные комбинации категорий, поэтому, если уникальных категорий много, код itertools.combinations сильно замедляется.
Число k возможных комбинаций для множества категориальных значений n определяется как:
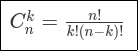
Вот почему XGBoost и LightGBM сокращают это число эвристически. Подробности читайте здесь.
Заключение
В работе с XGBoost или LightGBM я настоятельно рекомендую использовать нативную поддержку категорийных данных. Это не только более экономичный метод с точки зрения памяти и вычислений, еще он дает хорошую точность. Упрощается и конвейер подготовки данных: когда наборы данных для обучения и прогнозирования не пересекаются, он поддерживает пропущенные значения из коробки.
Data Science и Machine Learning
- Профессия Data Scientist
- Профессия Data Analyst
- Курс «Математика для Data Science»
- Курс «Математика и Machine Learning для Data Science»
- Курс по Data Engineering
- Курс «Machine Learning и Deep Learning»
- Курс по Machine Learning
Python, веб-разработка
- Профессия Fullstack-разработчик на Python
- Курс «Python для веб-разработки»
- Профессия Frontend-разработчик
- Профессия Веб-разработчик
Мобильная разработка
Java и C#
- Профессия Java-разработчик
- Профессия QA-инженер на JAVA
- Профессия C#-разработчик
- Профессия Разработчик игр на Unity
От основ — в глубину
А также


