В машинном обучении и нейронных сетях слои активации играют очень важную роль в процессе обработки данных. В этой статье мы рассмотрим, что такое слои активации, как они работают и как выбрать наиболее подходящий слой для вашей задачи.

Что такое слои активации?

Слои активации - это один из основных типов слоев, которые используются в нейронных сетях. Они представляют собой функцию, которая добавляет нелинейность к выходу предыдущего слоя. Это позволяет нейронной сети лучше моделировать сложные функции и более точно предсказывать результаты.

Как работают слои активации?

Слои активации принимают на вход результаты предыдущего слоя, называемые входом, и преобразуют их в выходное значение, которое передается следующему слою. Для этого они используют функцию активации, которая определяет, каким образом данные будут преобразованы.

Сигмойда

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры сигмоиды
x = np.linspace(-100, 100, 1000)
y = 1 / (1 + np.exp(-x))

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.title('График сигмоиды')

# Настраиваем значения осей координат
plt.xlim(-10, 10)
plt.ylim(0, 1)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=5)
plt.grid(True)

# Отображаем график
plt.show()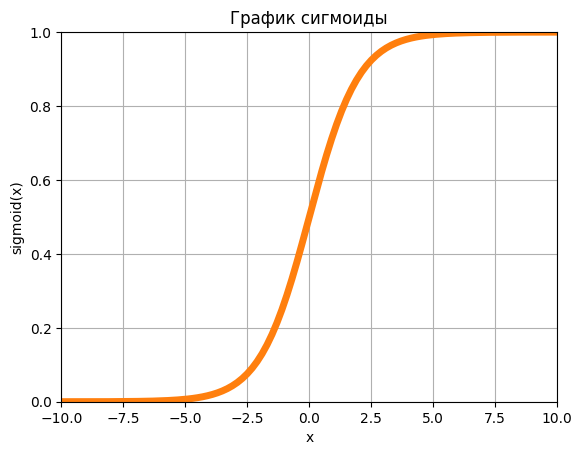

Сигмоидная функция активации - это нелинейная функция, которая преобразует входное значение в диапазоне от отрицательной бесконечности до положительной бесконечности в значение от 0 до 1. Эта функция активации часто используется в нейронных сетях для задач бинарной классификации.

Математически сигмоидная функция активации определяется следующим образом:

Графически сигмоидная функция активации выглядит как S-образная кривая, которая монотонно возрастает и имеет асимптоты на 0 и 1. В частности, если x > 0, то f(x) > 0.5, а если x < 0, то f(x) < 0.5. Значение 0.5 достигается при x = 0.

Сигмоидная функция активации используется для преобразования выходного значения нейрона в вероятность, т.е. вероятность того, что входное значение относится к классу 1, если мы работаем с задачей бинарной классификации. Если значение сигмоидной функции близко к 1, то вероятность того, что входное значение относится к классу 1, высока. Если значение близко к 0, то вероятность того, что входное значение относится к классу 1, низкая.

Однако сигмоидная функция активации имеет недостаток, который называется проблемой затухания градиента (vanishing gradient problem). Это означает, что при использовании сигмоидной функции активации в глубоких нейронных сетях градиенты могут становиться очень маленькими, что затрудняет обучение. В таких случаях часто используется другая функция активации, например, ReLU (Rectified Linear Unit).

ReLU

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры сигмоиды
x = np.linspace(-100, 100, 1000)
y = np.maximum(x, 0)

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.title('График функции ReLU')

# Настраиваем значения осей координат
plt.xlim(-5, 5)
plt.ylim(-0.5, 5)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=5)
plt.grid(True)

# Отображаем график
plt.show()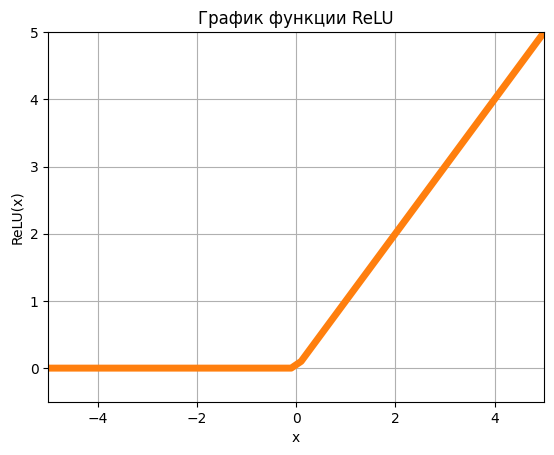

ReLU (Rectified Linear Unit) - это нелинейная функция активации, которая широко используется в глубоком обучении. Она преобразует входное значение в значение от 0 до положительной бесконечности. Если входное значение меньше или равно нулю, то ReLU выдает ноль, в противном случае - входное значение.

Математически ReLU определяется следующим образом:

где max - функция, возвращающая максимальное значение из двух.

Графически ReLU выглядит как линейная функция с нулевым отсечением на оси абсцисс в точке 0. Это значит, что функция имеет постоянный наклон во всех точках, кроме точки 0, где происходит отсечение.

ReLU имеет несколько преимуществ по сравнению со сигмоидной функцией активации. Во-первых, ReLU более вычислительно эффективна, поскольку она является простой и быстрой операцией, которая не требует вычисления экспоненты. Во-вторых, ReLU решает проблему затухания градиента, так как она не вызывает затухания градиента при обратном распространении ошибки, как это происходит в случае с сигмоидной функцией активации.

Однако, ReLU имеет некоторые недостатки. Во-первых, при использовании ReLU, некоторые нейроны могут "умереть" (dead neurons), т.е. они могут получить отрицательное значение и оставаться неактивными на всем протяжении обучения. Во-вторых, ReLU несимметрична относительно нуля, поэтому может возникнуть проблема "расслоения" (clustering), когда нейроны могут выдавать только положительные значения. Для решения этих проблем могут быть использованы другие функции активации, такие как Leaky ReLU или ELU.

Leaky ReLU

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры функции Leaky ReLU
x = np.linspace(-10, 10, 1000)
alpha = 0.1
y = np.where(x > 0, x, alpha*x)

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('Leaky ReLU(x)')
plt.title('График функции Leaky ReLU')

# Настраиваем значения осей координат
plt.xlim(-5, 5)
plt.ylim(-0.5, 5)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=5)
plt.grid(True)

# Отображаем график
plt.show()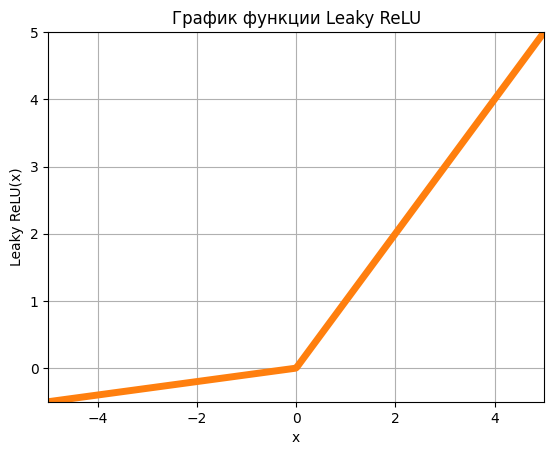

Leaky ReLU (Rectified Linear Unit) - это функция активации, которая используется в нейронных сетях для введения нелинейности в выходные данные каждого нейрона.

Обычный ReLU принимает входные значения и преобразует их, оставляя только положительные значения без изменения, а все отрицательные значения заменяет на 0. Однако у этого метода есть один недостаток, а именно "умирание ReLU". Это происходит в том случае, если входное значение отрицательное, то нейрон не будет активироваться и не будет вносить вклад в выходную функцию.

Для решения этой проблемы был разработан Leaky ReLU. В отличие от ReLU, Leaky ReLU возвращает само значение при положительном входном значении, а при отрицательных значениях возвращает линейную функцию от входа, умноженную на небольшой коэффициент, называемый отрицательным уклоном (leak). Таким образом, у нейрона всегда есть возможность вносить вклад в выходную функцию, даже если входные данные отрицательны.

Формула для Leaky ReLU выглядит следующим образом:

где a (alpha) - отрицательный уклон, который является маленьким положительным числом, например, 0,01.

Преимуществом Leaky ReLU является устойчивость к "умиранию" нейронов и лучшая сходимость в процессе обучения, что приводит к более быстрому и точному обучению нейронных сетей.

ELU

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры функции ELU
x = np.linspace(-10, 10, 1000)
alpha = 1.0
y = np.where(x > 0, x, alpha * (np.exp(x) - 1))

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('ELU(x)')
plt.title('График функции ELU')

# Настраиваем значения осей координат
plt.xlim(-5, 5)
plt.ylim(-2, 5)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=5)
plt.grid(True)

# Отображаем график
plt.show()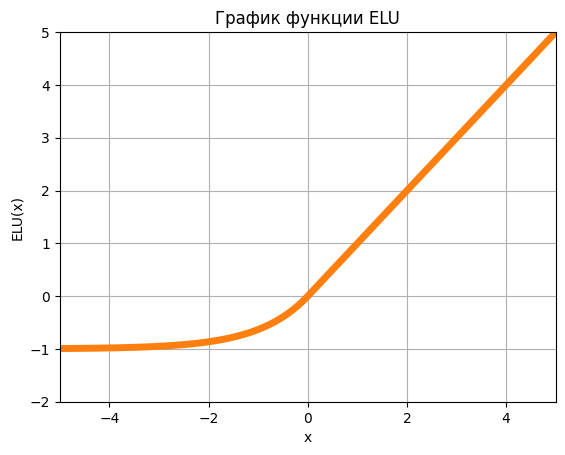

ELU (Exponential Linear Unit) - это функция активации, которая была предложена в 2015 году в статье "Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)". Она представляет собой измененную версию ReLU (Rectified Linear Unit), которая помогает ускорить обучение глубоких нейронных сетей и справляется с проблемой "мертвых нейронов" (dead neurons).

ELU определяется следующим образом:

где a (alpha) - это параметр, который может быть установлен в значение 1 по умолчанию.

ELU работает так же, как и ReLU, возвращая исходное значение входа, если он больше нуля. Однако, если значение входа меньше или равно нулю, то ELU использует экспоненциальную функцию, чтобы получить значение, которое ближе к нулю, чем значение, возвращаемое ReLU. Это позволяет избежать "мертвых нейронов" и ускорить обучение глубоких нейронных сетей.

Кроме того, ELU имеет свойство гладкости, которое так же помогает избежать проблемы "взрывающегося градиента" (exploding gradient), которая может возникать при использовании других функций активации, таких как ReLU. Это делает ELU более стабильной и более эффективной функцией активации для обучения глубоких нейронных сетей.

Однако, как и любая другая функция активации, ELU не подходит для всех задач и может давать неоптимальные результаты в некоторых случаях. Поэтому при выборе функции активации необходимо учитывать особенности конкретной задачи и проводить эксперименты для определения оптимальной функции.

SiLU

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры функции SiLU
x = np.linspace(-10, 10, 1000)
y = x * (1 / (1 + np.exp(-x)))

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('SiLU(x)')
plt.title('График функции SiLU')

# Настраиваем значения осей координат
plt.xlim(-5, 5)
plt.ylim(-1.5, 1.5)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=2)
plt.grid(True)

# Отображаем график
plt.show()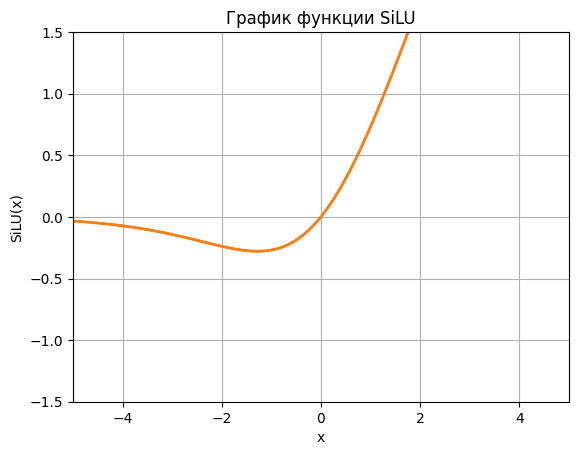

SiLU (Sigmoid-weighted Linear Unit) - это нелинейная функция активации, которая была предложена в 2017 году в статье "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning". SiLU сочетает в себе линейные и нелинейные свойства и имеет ряд преимуществ по сравнению с другими функциями активации.

Функция активации - это нелинейная функция, которая применяется к выходу каждого нейрона в нейронной сети. Она используется для добавления нелинейности в вычисления нейрона и позволяет модели учиться более сложным функциям. Различные функции активации могут влиять на скорость обучения модели, точность и стабильность её предсказаний.

Одной из самых распространенных функций активации является сигмоидная функция, которая представляет собой "сжимающую" функцию и применяется для преобразования значений в диапазон от 0 до 1. Однако, сигмоидная функция имеет некоторые недостатки, включая "затухание градиентов" и "эффект насыщения", что может затруднять обучение нейронных сетей.

SiLU - это функция активации, которая решает проблемы "затухание градиентов" и "эффект насыщения". Она является гладкой, монотонно возрастающей и не имеет "эффекта насыщения" как у сигмойдной функции, что позволяет модели обучаться более эффективно и быстро сходиться к оптимальному решению.

где: σ(x) - функция сигмойды, формула написанная ниже, и подробнее объяснена в пункте выше "Сигмойда".

В области компьютерного зрения SiLU часто используется в сверточных нейронных сетях (CNN), где она может помочь увеличить точность и скорость обучения моделей. Например, её используют в модели YOLOv8. Но, к сожалению, этой модели нет в библиотеки TensorFlow, и использовать её просто так, у вас не получиться.

Гиперболический тангенс

import numpy as np
import matplotlib.pyplot as plt

# Задаем параметры сигмоиды
x = np.linspace(-100, 100, 1000)
y = np.tanh(x)

# Строим график
plt.plot(x, y)

# Настраиваем оси координат и заголовок
plt.xlabel('x')
plt.ylabel('tanh(x)')
plt.title('График гиперболического тангенса')

# Настраиваем значения осей координат
plt.xlim(-10, 10)
plt.ylim(-1, 1)

# Строим график, настраиваем ширину линии и добавляем сетку
plt.plot(x, y, linewidth=5)
plt.grid(True)

# Отображаем график
plt.show()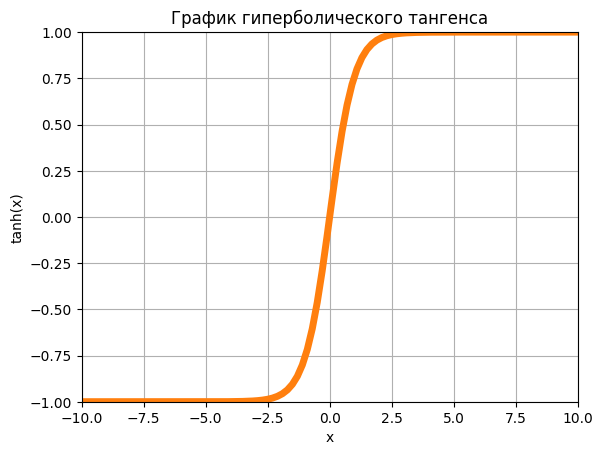

Гиперболический тангенс (tanh) является одной из наиболее распространенных функций активации в нейронных сетях. Он используется как для классификации, так и для регрессии, а также для обработки изображений и других типов данных.

Это функция активации, которая преобразует входные значения в диапазоне от -1 до 1. Формула для вычисления гиперболического тангенса выглядит следующим образом

Гиперболический тангенс очень похож на сигмоидальную функцию, которая также используется в нейронных сетях. Он принимает входные значения и преобразует их в диапазон от -1 до 1, что может использоваться для задач регрессии. Значения, близкие к -1, интерпретируются как отрицательные значения, а значения, близкие к 1, как положительные значения. Значения, близкие к нулю, обрабатываются как нейтральные.

По сравнению со сигмоидальной функцией, гиперболический тангенс имеет более пологую кривую, что позволяет сети лучше распознавать сложные зависимости в данных. Также гиперболический тангенс имеет гладкую производную, что позволяет использовать алгоритмы оптимизации, которые требуют вычисления градиента.

Softmax

К сожалению, функция Softmax визуально представляется в виде кривой, что затрудняет ее графическое отображение на графике. Поэтому будет демонстрация на примере заданного вектора.

import numpy as np
import matplotlib.pyplot as plt

def softmax(z):
    # Преобразуем вектор в массив, чтобы избежать ошибок типа "integer division or modulo by zero"
    z = np.array(z)
    # Вычисляем экспоненты каждого элемента вектора
    exp_z = np.exp(z)
    # Вычисляем сумму экспонент всех элементов вектора
    sum_exp_z = np.sum(exp_z)
    # Вычисляем вероятности для каждого элемента вектора
    softmax_z = exp_z / sum_exp_z
    return softmax_z

# Задаем входной вектор
z = [1, 2, 3, 4, 1, 2, 3]
# Вычисляем значения Softmax
softmax_z = softmax(z)

# Выводим значения на экран
print("Softmax(z) =", softmax_z)

# Строим график вероятностного распределения
plt.bar(range(len(z)), softmax_z)
plt.title("Softmax Distribution")
plt.xlabel("Class")
plt.ylabel("Probability")
plt.show()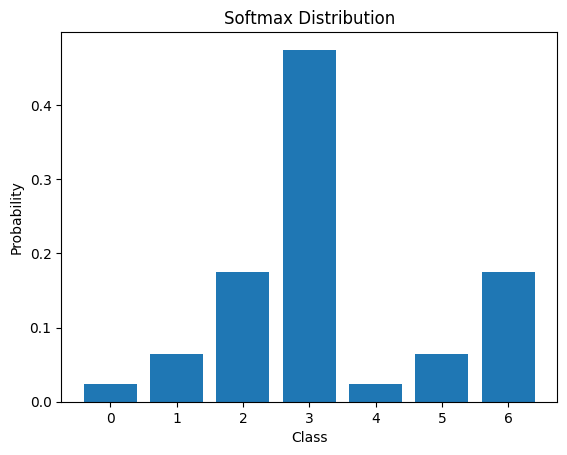

В этом примере мы задаем входной вектор z, затем вычисляем значения с помощью функции softmax(). Затем мы выводим значения на экран и строим график вероятностного распределения. График отображает вероятности для каждого элемента входного вектора в виде столбчатой диаграммы. Более детальные значения, вы можете увидеть ниже:

Softmax(z) = [0.02364054 0.06426166 0.1746813 0.474833 0.02364054 0.06426166 0.1746813 ]

Функция Softmax используется для преобразования вектора значений в вероятностное распределение, которое суммируется до 1. Она особенно полезна в многоклассовой классификации, где необходимо определить вероятности для каждого класса.

Формула функции Softmax выглядит следующим образом:

где z_i - это элемент входного вектора, а k - это общее число элементов в векторе.

График функции Softmax представляет собой гладкую кривую, начинающуюся от 0 и заканчивающуюся на 1, что соответствует сумме вероятностей всех элементов вектора. Кривая функции Softmax имеет свойство, что вероятность любого элемента вектора увеличивается, если значения других элементов уменьшаются, что позволяет использовать эту функцию для многоклассовой классификации.

Хотя функция Softmax имеет множество применений в машинном обучении, она также может иметь недостатки, такие как чувствительность к выбросам и несбалансированным данным, что может приводить к неверным вероятностным оценкам.

Как выбрать подходящий слой активации?

Выбор подходящего слоя активации зависит от задачи машинного обучения, типа данных и модели, которую вы хотите создать. Вот несколько рекомендаций, которые могут помочь в выборе подходящего слоя активации:

1. Для задач классификации, используйте Softmax, если вы хотите получить вероятности классов в качестве выходных данных. Используйте Sigmoid или Tanh, если вы хотите получить двоичный вывод.

2. Для задач регрессии, используйте ReLU или его модификации, такие как LeakyReLU или ELU. Эти функции обычно дают лучшую производительность в задачах регрессии.

3. Для моделей глубокого обучения, ReLU является общим выбором для скрытых слоев, так как она может ускорить обучение, но можно также использовать другие функции, например, PReLU или Swish.

4. Для рекуррентных нейронных сетей, обычно используются функции активации Tanh.

5. Если вы не уверены, какую функцию активации использовать, попробуйте использовать несколько функций активации и сравните их производительность на валидационном наборе данных.

6. Кроме того, при выборе функции активации необходимо учитывать свойства функции, такие как производная, способность обеспечивать нелинейность и способность предотвращать затухание градиента.

В целом, выбор подходящего слоя активации зависит от конкретной задачи и экспериментальных результатов. Необходимо тщательно подбирать функцию активации и изменять ее, чтобы получить оптимальные результаты для вашей модели.

Важно также помнить, что выбор подходящего слоя активации может зависеть от структуры и архитектуры вашей нейронной сети, а также от данных, на которых вы обучаете модель. Поэтому важно экспериментировать с разными функциями активации и выбирать ту, которая работает лучше всего для вашей конкретной задачи.

В заключение, слои активации являются одним из ключевых элементов в нейронных сетях, которые позволяют моделировать сложные функции и более точно предсказывать результаты. В этой статье были перечислены далеко не все виды слоев активации, а только те, что наиболее популярны, на слуху, или я сам лично использовал их в своей работе.

Спасибо за прочтение!