Привет, Хабр!

С вами Дворников Дмитрий — Data Scientist и участник профессионального сообщества NTA.

Подход, о котором я расскажу, позволяет расширить функциональные возможности метода Наивного Байеса благодаря использованию весовых коэффициентов для различных групп признаков объекта датасета (модель может обучаться не только на отдельных словах в тексте, но также на некоторых метаданных, таких как авторы текста и источник информации).

С помощью разработанной ML‑модели можно улучшить качество классификации текстов при использовании обучающей выборки небольшого объёма (всего 30 объектов) и сократить время обучения модели.

Задача решалась в рамках разработки системы рекомендаций научных статей. Наработки могут быть использованы в любых задачах NLP и Text Mining.

План поста

• Введение

• Постановка задачи

• Что будем делать

• Матчасть

• Эксперименты

• Интерпретация результатов

• Заключение

Предыстория

Этот пост является адаптацией исследования, проведённого мной и моими коллегами, для широкой русскоязычной аудитории. Результаты исследования были представлены на конференции TELE2022, и опубликованы в IEEE Xplore. Полный текст оригинальной публикации доступен на ResearchGate. Код исследования ML‑модели ждёт своего часа на GitHub.

Далеко не каждый IT‑специалист настолько искушён специализированной литературой, что предпочитает вместо Stack Overflow или Habr листать материалы бесчисленных конференций. Научные тексты отличаются исключительной сухостью, строгостью, сдержанностью, даже скупостью на пояснения (не говоря уже об эпитетах и метафорах) и порой, чтобы добраться до сути, читателю приходится пробираться через тонны формальных определений.

Поэтому в этом посте, помимо разбора модификации Наивного Байеса для системы рекомендаций, я постараюсь показать, что наука — это не только просто, но и увлекательно.

Кому будет интересно

Порог вхождения у этого поста относительно невысокий — достаточно уметь подавлять панику при виде математических обозначений и быть знакомым с азами машинного обучения. Если вас не смущают верхние и нижние индексы у букв, знак математической суммы не вызывает инстинктивного отторжения, и вы не просите у Data Scientist'а назвать все даты, то всё будет хорошо.

Матёрым же ML‑разработчикам пост предложит свежий взгляд на классические методы машинного обучения, а также даст простор для идей, замечаний и предложений.

Кроме того, уверен, что и просто любопытствующие умы узнают что‑то новое и с пользой проведут досуг.

Введение

Искусственный интеллект настолько прочно вошёл в нашу жизнь, что уже трудно представить, как мы справлялись без него (мы не справлялись). Ни одна поисковая система не обходится без умных алгоритмов, медиасервисы теперь в курсе ваших предпочтений и наперебой предлагают что‑нибудь послушать/посмотреть/почитать, интернет‑магазины, контекстная реклама — тысячи моделей машинного обучения борются за ваше внимание каждый день или помогают вам принимать небольшие решения.

Это уже не блажь, а необходимость. Данных стало настолько много, что переварить такой объём информации наш мозжечок просто не в состоянии (да простят меня нейробиологи), не говоря уже о том, чтобы усвоить полезные знания.

Я не зря заострил внимание именно на ранжирующих моделях выше.

Ранжирующие модели

Класс моделей машинного обучения, предназначенных для упорядочивания элементов в некоторой последовательности по заданному признаку. Например, коллекции видеоигр по степени похожести на «GTA V».

Интуиция работы таких алгоритмов — взять два объекта, сравнить их между собой и вернуть тот, что больше соответствует заданному нами критерию отбора. А если сравнить все элементы последовательности друг с другом попарно и разложить их по порядку, то получится упорядоченный набор объектов.

В этом ранжирующие модели очень похожи на нас с вами: они борются с растущей энтропией и всеми силами пытаются организовать какой‑нибудь порядок.

Даже если у вас в квартире царит творческий беспорядок, то это лишь значит, что вы отранжировали свои дела так, что уборка оказалась в вашем ToDo‑листе где‑то на позиции со значением индекса, стремящимся к бесконечности.

Постановка задачи

Хотите собственную новостную ленту? А может, вас заинтересуют персональные книжные рекомендации? Решили начать читать научные статьи, но вам нужны только самые интересные? В этом вам поможет NLP. И речь не о нейролингвистическом программировании.

NLP

Natural Language Processing (NLP) – это, в узком смысле, совокупность методов обработки естественного языка. То есть того языка, на котором говорят, пишут и думают люди.

Смысл этого огромного направления в ML – если уж не научить компьютер понимать человеческую речь, то хотя бы создать иллюзию, что он умеет это делать.

Задача состоит в том, чтобы алгоритм запоминал, какие тексты нам нравятся, а какие нет, и ранжировал новые тексты по предполагаемой релевантности для нас. Для этого ему необходимо как‑то эту релевантность оценивать. Это должно быть число, чтобы разные релевантности можно было между собой сравнивать.

При этом желательно, чтобы обучающая выборка (тексты, на которых модель будет учиться) была как можно меньше, а точность рекомендаций — как можно выше.

Конечно, хорошо, если вы много чего прочли и вам есть что рассказать алгоритму. Но процесс формирования (разметки) датасета в этом случае станет невыносимым: вам придётся вбить в систему сотни, а то и тысячи текстов с проставленными «лайками» и «дизлайками».

Вообще, это стандартная ситуация для машинного обучения, когда нужно много данных. Но нас это не устраивает. Мы пойдём другим путём.

Что будем делать

Мы осуществим некоторое колдунство над Наивным Байесом и превратим его в ранжирующую модель, а ещё изобретём адаптивный механизм формирования обучающей выборки.

Наивный байесовский классификатор

Это простая ML-модель, оценивающая вероятность принадлежности текста определённому классу (например, «релевантный» и «нерелевантный») исходя из частоты употребления различных слов.

В основе этой модели лежит «наивное» предположение о том, что слова друг с другом никак не связаны. Метод славится своей простотой и эффективностью в правильно поставленных задачах.

Матчасть

В этой части я расскажу:

• о том, на какой подвиг мне пришлось пойти ради науки;

• как устроен Наивный Байес и как его можно прокачать;

• что будем делать с данными;

И на закуску — рубрика «Эксперименты».

Датасет

Мы будем анализировать аннотации к статьям на английском языке (его проще обработать), найденным по запросу «Brain Cancer MRI» с фильтром по области знаний «Computer Science» из Semantic Scholar Open Research Corpus (релиз от 01.09.2021). Это open‑source сборник статей, сформированный специально для задач NLP и Text Mining.

Text Mining

Text Mining обычно переводят на русский язык как «интеллектуальный анализ текста».

Это обширное направление в искусственном интеллекте, посвящённое вопросам извлечения, суммаризации, поиска и т. д. полезной информации из корпуса документов.

Мы ищем публикации, связанные с обработкой снимков МРТ головного мозга человека (магнитно-резонансная томография) компьютерными методами с целью выявления злокачественных образований. Стоит учесть, что в ответ на наш запрос могут попасть нерелевантные статьи:

• с анализом головного мозга других животных;

• с классификацией уже выявленного злокачественного образования;

• на сторонние темы (например, в которых ключевое слово употребляется всего один раз).

Кроме того, интересующие нас публикации могут и почти не содержать заданных ключевых слов («Brain Cancer MRI»), зато в избытке содержать другие, о которых мы не догадываемся (например, «malignant» — злокачественный). При этом мы не хотим потерять статьи, которые этих дополнительных слов не содержат, но всё ещё нас интересуют. Поэтому вместо того, чтобы бесконечно множить ключевые слова в запросе и фильтры, мы и делегируем эту задачу ML‑модели.

Всего по запросу нашлось 499 публикаций. Я внимательно прочёл аннотацию к каждой, оценил её релевантность флажком «да/нет» и поместил весь датасет в формат JSON (доступен на GitHub, датасет занимает 2.41 MB). Пришлось даже написать для этой цели небольшое консольное приложение.

Для анализа были отобраны заголовок статьи (title), аннотация (paperAbstract), список авторов (authors), название журнала/конференции (journalName) и области знаний (fieldsOfStudy). Выглядит датасет следующим образом:

[ …,
  {
    "id": "96f93890dc72f65e7ca41a827918b17dc2b0d6a1",
    "title": "Brain MRI Image Classification using Image Mining Algorithms",
    "paperAbstract": "Nowadays, diagnosis and treatment of deadly cancer diseases are based on symptoms and radiological appearance. There are many […]",
    "authors": [ …,
      {
        "name": "Vaibhavi  Solanki",
        "ids": [ …,
          "52155233"
         …, ]
      },
    …, ],
    "journalName": "2018 Second International Conference on Computing Methodologies and Communication (ICCMC)",
    "fieldsOfStudy": [ …,
      "Computer Science"
    …, ],
    "match": 1
  },
…, ]

Для того чтобы мы могли как‑то идентифицировать статью, добавлен атрибут «id». Поле «match» и является тем самым флагом релевантности, где 1 означает «да», а 0 — «нет».

Единственное, что вас может смутить, — это список идентификаторов «ids» у каждого автора. Здесь всё очень просто: корпус научных статей является сборной солянкой данных, полученных из разных источников, поэтому у одного и того же автора может быть несколько идентификаторов в различных системах.

Старый добрый и наивный

Идея Наивного Байеса заключается в расчёте вероятности принадлежности статьи X_iклассу Q_k  по формуле 1 приведённой ниже, исходя из частоты встречаемости каждого слова в статьях соответствующего класса. Классов у нас два: «релевантный» и «не релевантный».

где P(Q_k) — вероятность нахождения статьи класса Q_k в корпусе документов (доля статей класса Q_k в корпусе документов), рассчитываемая по формуле 2,

P(xj|Q_k) — вероятность принадлежности слова x_j статье класса Q_k, рассчитываемая по формуле 3,

X — множество всех документов в корпусе,

M — количество слов (уникальных) в корпусе документов.

Простыми словами, каждое слово вносит определённый вклад в конечную оценку релевантности (или нерелевантности) статьи в зависимости от того, насколько часто оно встречалось в других релевантных (или нерелевантных) статьях: чем чаще — тем, вероятно, более релевантно (или менее релевантно). За этот расчёт отвечает формула 3.

При этом если релевантных (или нерелевантных) статей в обучающей выборке, в принципе, оказалось больше, то алгоритм считает, что вероятность встретить именно такие статьи (релевантные или нерелевантные) тоже больше. (Что логично и относится к вопросу о вероятности встретить чёрного лебедя). В этом и состоит смысл первого множителя в формуле 1. Вот она:

где X' — множество документов в корпусе, на которых была обучена ML‑модель (обучающая выборка),

N — количество статей в обучающей выборке,

α ϵ (0, 1] — параметр сглаживания.

По сути, это просто доля релевантных (или нерелевантных) статей в обучающей выборке. Параметр сглаживания нужен на тот случай, если каких-то статей в выборке не окажется, – так мы избежим нулевых вероятностей. Математики всё предусмотрели.

И наконец, мы добрались до самой сложной для понимания формулы:

где N_jk — количество вхождений слова x_j в статьи класса Q_k на которых была обучена ML-модель (статьи из обучающей выборки),

N_k — общее количество слов, входящих в статьи обучающей выборки класса Q_k,

M — общее количество слов в обучающей выборке.

Здесь пара (N_jk, N_k) отвечает за расчёт некоторого коэффициента влияния определённого слова. То есть, опять же, чем чаще слово употребляется, тем выше его влияние на конечную оценку релевантности.

А вот пара (α, αM) выполняет роль уже знакомого нам сглаживания на случай, если встреченного слово вообще не было в обучающей выборке. Спойлер: для любого такого неизвестного слова формула № 3 выдаёт один и тот результат. Это логично, нет смысла как‑то по‑особенному обрабатывать каждое незнакомое слово.

На этом моменте я рекомендую сделать перерыв, чтобы всё уложилось в голове!

«Автор» – это больше, чем слово

Не возникло ли у вас диссонанса, когда после обзора датасета с кучей полей вы посмотрели на такие простые и понятные формулы? Как одно соотнести с другим? Вот и у меня в своё время возник такой вопрос.

Можно разбить на слова заголовок и аннотацию.

Но что делать с авторами, названием журнала и областями знаний? Тоже токенизировать? На мой взгляд, мы можем сделать кое‑что поумнее. Мы можем придать им вес!

Токенизация в NLP

Процесс разбиения текста на отдельные слова (предложения, буквы и т. д., в зависимости от задачи) — токены/термы.

Согласитесь, ведь если автор написал отличную статью на интересующую нас тему, то вероятность того, что другая его статья тоже вам понравиться уже точно больше нуля. То же самое относится и к журналу, в котором статья опубликована, и к областям знания.

Поэтому мы разобьём признаки на четыре большие группы: слова, авторы, журналы и области знаний:

Для каждой статьи будет рассчитано, в каком количестве в ней встречаются какие слова, а также будут проставлены отметки соответствия [0/1] по авторам, журналам и областям.

И теперь научим Наивного Байеса весовым коэффициентам.

Уже не такой наивный

В связи с разбиением термов на четыре группы (слова, авторы, журналы и области знаний), мы модифицируем НБ таким образом, чтобы для различных групп могли ставится различные весовые коэффициенты. Формулы 1 и 3 превращаются в уравнения 4 и 5, соответственно.

где w^l — весовой коэффициент группы G_l,

x _j^l — терм группы G_l.

То есть уже знакомые нам вероятности возводятся в степень весового коэффициента. Но будьте осторожны! Так как вероятность всегда лежит в пределах [0, 1], то чем больше весовой коэффициент, тем меньшее значение получается при возведении в степень. Соответственно, наибольшее значение вероятности (единица) получается при нулевом весовом коэффициенте.

Понимаю, это несколько контринтуитивно. Поэтому можете использовать такой вариант определения весового коэффициента — 1/w^l. Просто я не хотел перегружать и без того информативное уравнение.

Далее:

где N_jk^l— количество вхождений терма x_j группы G_l в статьи класса Q_k, на которых была обучена ML‑модель (статьи из обучающей выборки),

N_k^l— общее количество термов группы G_l, входящих в статьи обучающей выборки класса Q_k

Здесь отличие лишь в том, что вероятность рассчитывается по отдельным группам, о чём со всей очевидностью свидетельствует верхний индекс l.

ML-модель под ключ

Как вы думаете, какую в среднем оценку релевантности вы будете получать при таком подходе? «Эта статья релевантна с вероятностью 82%. С уважением, Джарвис»? Как бы не так!

Слов (токенов/термов) будет настолько много и они так редко будут повторяться, что вероятности будут находится где‑то в пределах от 0.0 000 000 000 001 до 0.0 000 000 001, а то и меньше. Для удобства работы с такими малыми числами выражения логарифмируют, что позволяет оперировать не самими числами, а с их порядками.

Соответственно, для модифицированной версии НБ логарифмируется выражение 4.

Вы можете спросить: «Если у всех этих статей почти нулевая вероятность оказаться релевантными, то как алгоритм вообще нам хоть что‑то порекомендует?» Отвечаю. Вы забыли, что мы считаем сразу две вероятности: и релевантности, и нерелевантности. А они, по нашему «наивному» предположению, друг от друга не зависят. Поэтому мы можем их сравнить. И какая больше — та и победит:

Ещё я обещал представить байесовскую модель ранжирования. Здесь тоже ничего сложного:

Каждая статья получает некоторую оценку релевантности, по которой ранжируется весь список документов.

Рубрика "Эксперименты"

Первым делом нужно будет выбрать лучшие гиперпараметры для ML‑модели. Это параметр сглаживания α и четыре весовых коэффициента w_words, w_autors, w_journals и w_frields. Но это не самое интересное.

Эксперимент №1. Полный перебор

Цель эксперимента: определить минимальный объём обучающей выборки, при котором ML‑модель сходится — то есть даёт приемлемую точность классификации (~70%).

Так как мы разрабатываем модель для системы рекомендаций, то нас интересует именно точность — насколько точны будут эти рекомендации, с какой вероятностью рекомендация понравиться пользователю.

Где-где сходится?

В математике под сходимостью подразумевается существование некоторого пределах у числовой последовательности или бесконечного ряда.

Здесь понятие сходимости употребляется скорее в метафорическом смысле и означает, что функция «дотягивается» до некоторого заданного нами порогового значения.

Последовательно значение объёма обучающей выборки меняется от 5 до 390 (~80% от объёма датасета). Для оценки эффективности работы ML‑модели при заданном значении объёма обучающей выборки применяется стохастическая валидация.

Стохастическая валидация

Авторский механизм валидации ML‑модели, отличающийся от классической кросс‑валидации случайным и многократным дроблением датасета на обучающую и тестовую выборки (на k‑folds).

Потребность в таком подходе возникает, когда обучающая выборка крайне мала по сравнению с размером всего датасета и поочерёдное включение в неё каждого объекта не представляется целесообразным.

Иными словами, так быстрее и получается некое подобие bootstrap‑выборки.

Эксперимент №2. Имитация работы пользователя

Цель эксперимента: определить минимальный объём обучающей выборки, при котором ML‑модель сходится (точность ~70%), в условиях имитации интерактивной работы пользователя с системой рекомендаций.

В предыдущем эксперименте обучающая выборка формировалась случайно, но в реальности пользователь сам выбирает, какие статьи ему читать и оценивать. Причём, выбирает он, как правило, статьи с релевантным названием (потенциально имеющие класс «1»), а остальные (потенциально имеющие класс «0») игнорирует.

Для нас это значит, что в реальности мы будем иметь несбалансированную обучающую выборку, и нам интересно, как алгоритм справится с этой задачкой.

Допустим, каждые пять статей пользователь обновляет рекомендации. Тогда в топ попадают наиболее релевантные, по мнению ИИ, статьи. Пользователь снова просматривает первые пять, и цикл повторяется с дополненной обучающей выборкой.

Эксперимент №3. Active Learning

И наконец, квинтэссенция всех наших с вами измышлений – адаптивный механизм. После обновления рекомендаций ИИ выводит в топ как наиболее релевантные, так и наименее релевантные статьи на суд пользователя. Таким образом, шансы итеративного формирования сбалансированной обучающей выборки должны резко повыситься.

Звучит сложновато, да?

Короче говоря, сначала мы показываем пользователю четыре (условно) рандомные статьи и собираем обратную связь (какие оказались релевантными, а какие нет). Затем запускается первый круг обучения, статьи из очереди заново ранжируются, и мы показываем пользователю ещё по две статьи из начала и из конца списка. Он снова их оценивает, обучающая выборка насчитывает уже целых 8 статей… И так далее.

На этом наука заканчивается. Теперь посмотрим на результаты всех этих экспериментов.

Результаты

Подбор гиперпараметров

Лучшей оказалась комбинация следующих гиперпараметров: α = 0.5, w_words = 1, w_autors = 1, w_journals = 0 и w_frields = 0.

Такой результат может свидетельствовать как о реальной пользе взвешивания признаков авторства, так и о статистической погрешности. Также возможно, что датасет был настолько невелик, что значительных пересечений по журналам и областям среди релевантных статей просто не наблюдалось.

Отмечаем, что требуется дополнительное исследование и оценка перспективности идеи.

Эксперимент №1. Полный перебор

По графику медианных значений видно, что ML-модель начинает сходиться (presicion => 70%)  при объёме обучающей выборки (ОВ), равном примерно 30 статьям.

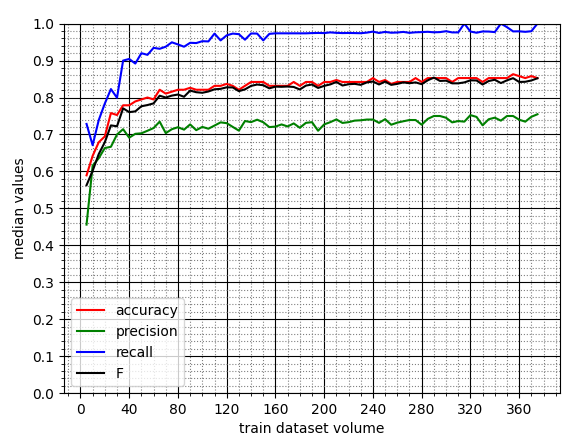
Это неплохой результат, особенно если учесть, что дальше точность растёт с переменным успехом и достигает ~75%. Также отметим высокое значение полноты (более 90%), что говорит о почти полном покрытии релевантных статей.

Эксперимент №2. Имитация работы пользователя

По графику медианных значений видно, что сходимость (presicion => 70%) ML‑модели наступает при объёме ОВ, равном 44 статьям. Затем точность незначительно колеблется, не превышая, однако, при этом 70%.

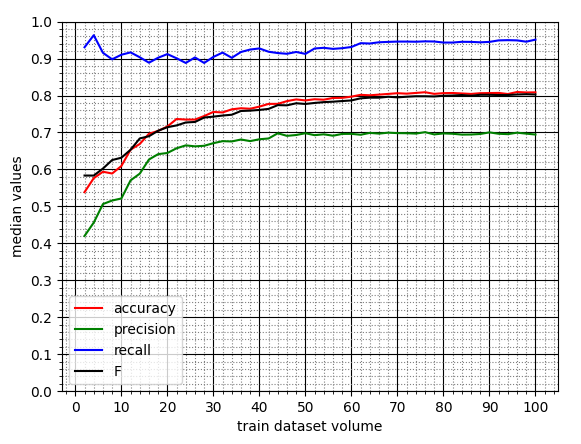
То есть в реальности нам следует ожидать: во‑первых, снижения максимальной точности с 75% до 70%; а во‑вторых, для достижения приемлемой точности рекомендаций потребуется больше статей (44 вместо 30).

Тем не менее, результаты стали более прогнозируемыми. Об этом свидетельствует более сглаженный график.

Посмотрим, получилось ли у нас как‑то купировать сниженную точность модели с помощью адаптивного механизма.

Эксперимент №3. Active Learning

Тут сходимость ML‑модели (presicion => 70%) наступает немного раньше — при объёме ОВ, равном 30 статьям, — как в первом эксперименте. Однако затем точность также испытывает колебания от 70% в меньшую сторону.

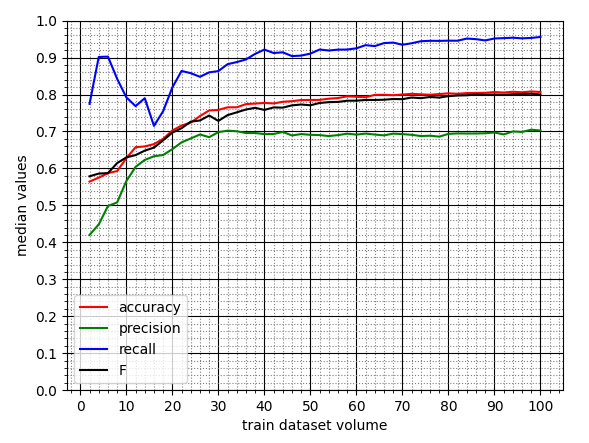
То есть частично решить проблему всё‑таки удалось. И результаты тоже более прогнозируемые. Только вот этот прогноз снизился на ~5% по сравнению с первым экспериментом, да и то еле‑еле дотягивает до приемлемого уровня.

Интерпретация результатов

Можно с уверенностью сделать вывод, что модифицированный Наивный Байес неплохо справляется с ранжированием научных публикаций по заданной тематике после небольшой калибровки путём обучения на всего лишь 30 примерах.

По всей видимости, обучать модель нужно на рандомных статьях — так шанс приемлемой точности рекомендаций немного больше (~75%).

Потенциально взвешивание групп признаков может повысить эффективность модели на больших наборах данных и вообще расширить возможности Наивного Байеса.

Гипотеза о пользе адаптивного механизма формирования сбалансированной обучающей выборки по сравнению с рандомизированной не подтвердилась. Отрицательный результат — тоже результат. Это наука, здесь так можно и нужно.

Заключение

Мы рассмотрели модификацию Наивного Байеса, позволяющую ранжировать тексты по релевантности; поняли, как устроены системы рекомендаций под капотом; перестали бояться умных слов и прониклись романтикой путешествия по чертогам собственного разума; но главное — поняли, что наука доступна каждому.

Спасибо всем, кто продержался до конца! Вы умники и умницы! Всех остальных я тоже понимаю.