Всем привет.
Я ML энтузиаст, и пытаюсь разобраться в нейронных сетях. Пока разбирался у меня появились вопросы, а возможно и ответы.
Собственно, сразу один из моих вопросов: почему перцептрон с несколькими выходами не используется по умолчанию?
TL;DR основная идея
Количество параметров полносвязного нейронного слоя можно сократить почти** не потеряв в точности!
Для этого вместо привычного нейрона нужно использовать нейрон с несколькими выходами(будем называть его "новый").
Был нейрон:
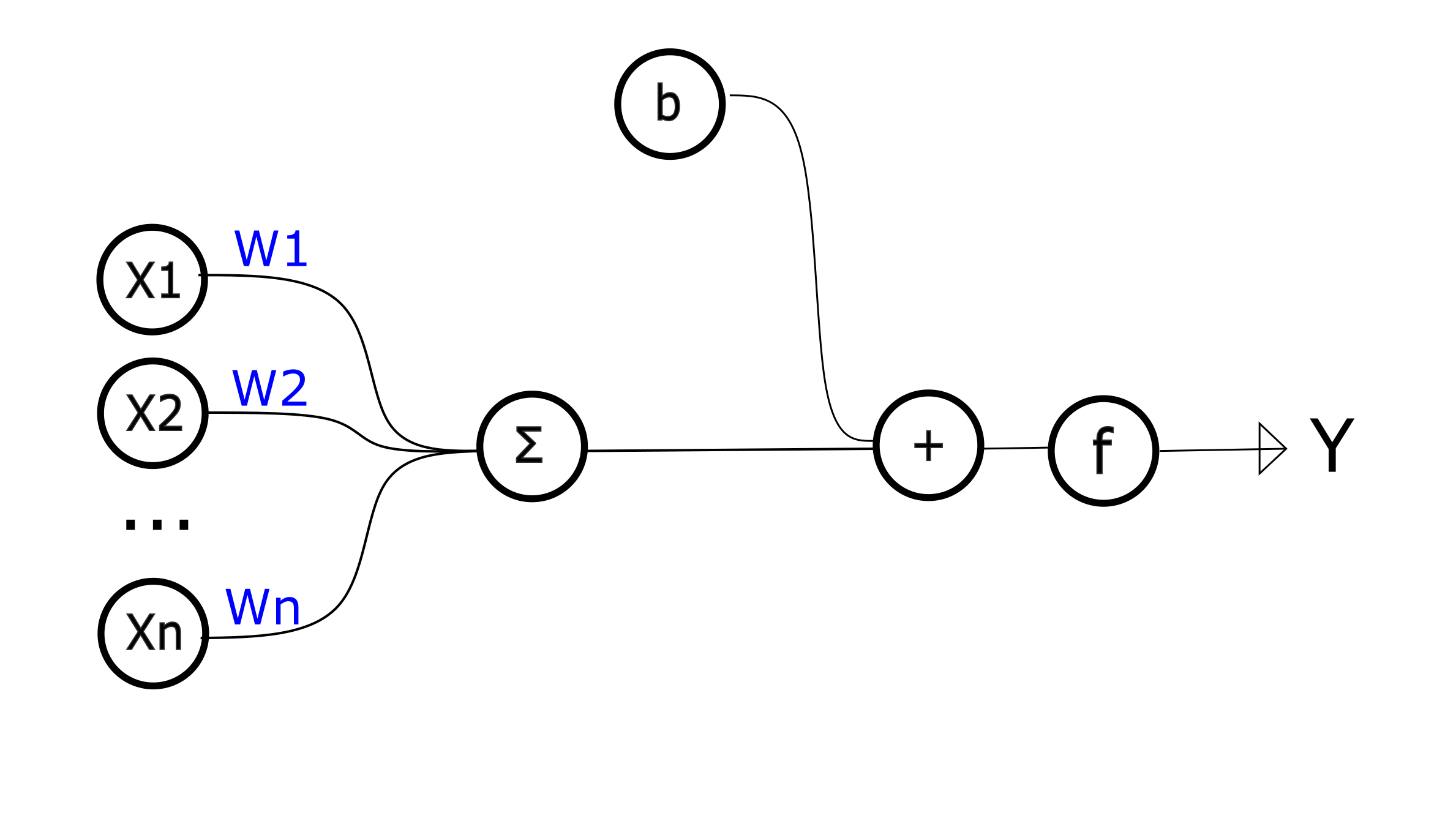
Стал нейрон:
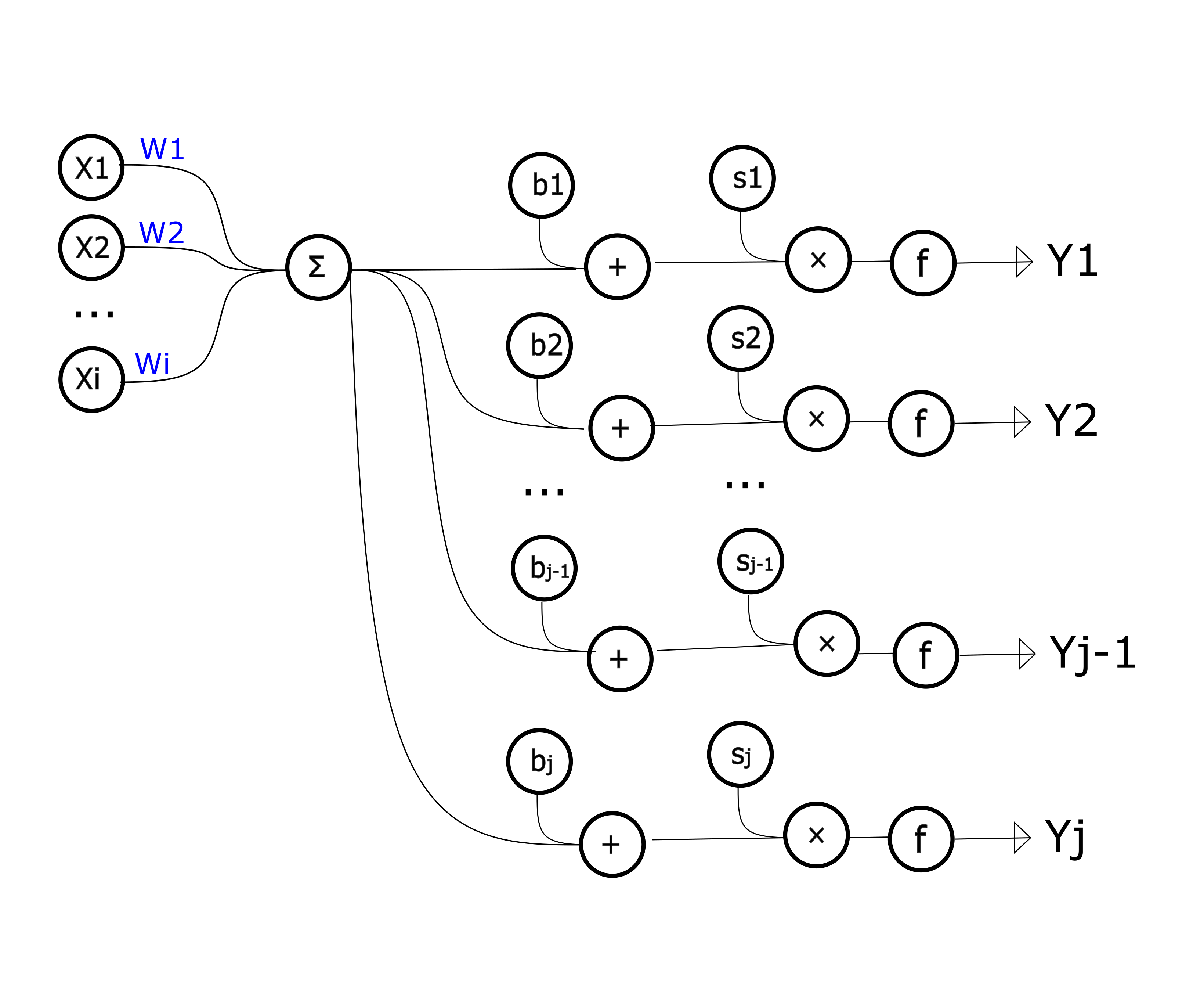
Новый нейрон состоит из вектора W(Нормали к поверхности), нескольких пар значений: [смещения гиперплоскости b, масштаба расстояния s] и функции активации.
Самым "тяжеловесным" в обычном перцептроне является вектор нормали W.
Соответственно, в "новом" нейроне предпринимается попытка экономии кол-ва параметров как раз за счет переиспользования нормали W несколько раз.
Пусть n_surface_normal_reuse будет обозначать количество переиспользований нормалей, он же количество выходов у перцептрона.
Теперь считаем сколько параметров имеет слой из классических нейронов и слой из "новых" перцептронов при равном количестве входов и выходов.
#слой из обычных перцептрона
i = 1000 # количество входов каждого слоя
o = 1000 # количество выходов каждого слоя
n = o # количество нейронов каждого слоя
w = i * n # количество параметров матрицы W для слоя
b = o # количество параметров смещений Bias
print(w + b) # количество параметров слоя
1001000 ~ миллион параметров
#слой из "новых" перцептронов
i = 1000 # количество входов слоя
o = 1000 # количество выходов слоя
n_snr = n_surface_normal_reuse = 10 # количество выходов одного нейрона
b = o # количество параметров смещений гиперплоскости bias
s = o # количество параметров растяжений растояния до гиперплоскости scale
n_w = o/n_snr # количество нормалей к поверхности
w = n_w * i # количество параметров слоя матрицы W
print(w + b + s) # количество параметров слоя
102000.0 ~ сто тысяч параметров
Количество параметров в данном случае сократилось примерно в n_surface_normal_reuse раз.
Рассуждения/Доказательство
Смотрим на текущий общепринятый простой перцептрон:
y = activate_f(ΣWi*Xi + b)
Чтобы лучше понимать что скрывается за этой формулой я я прибегну к различным интерпретациям.
Итак:
ΣWi*Xi + b = 0, есть ничто иное как гиперплоскость.
Если b = 0, то плоскость проходит через центр координат, а нормалью к этой гиперплоскости является вектор W.
Другими словами, вектор нормали W определяет углы(или повороты) гиперплоскости относительно системы координат.
Параметр b - влияет на параллельное смещение гиперплоскости относительно начала координат.
Cмотрим на расстояние от гиперплоскости до точки X (её координаты - это входной вектор нейрона [X1, X2,... X3]) .
Формула расстояния выглядит как
(ΣWi*Xi + b) / ((ΣWi2)0.5)
Видно что в числителе наша формула обычного нейрона: ΣWi*Xi + b
Введем новый параметр scale = 1 / (ΣWi2)0.5, и перепишем формулу обычного перцептрона : \
y = activate_f((ΣWi*Xi + b) * s), где W - нормаль, b-смещение(bias), s - масштаб(scale).
Смотрим на перцептрон новыми глазами, видим что в нем:
a) считается расстояние от входной точки до гиперплоскости заданной вектором W и смещением b,
б) полученное расстояние масштабируется( растягивается или сжимается), за это отвечает параметр s,
в) Функция активации в свою очередь - просто принимает на вход "расяннутое" или "сжатое" расстояние от входной точки до гиперплоскости и "искажет" его.
Расстояние, пропущенное через функцию активации, позволяет перевести число, которым выражено расстояние, в термины: далеко/близко, чем дальше тем лучше, берем по одну сторону/по другую не берем, и т. д.
Набор терминов зависит от выбранной функции активации, например:
если функция активации Relu, то ее можно перевести в следующие теримины: берем точки ТОЛЬКО С ПОЛОЖИТЕЛЬНОЙ СТОРОНЫ(куда смотрит вектор Нормали W), и чем дальше точка - тем лучше
Sigmoid - не берем точки, которые ДАЛЕКО ПО ОТРИЦАТЕЛЬНУЮ сторону, точно берем точки что ДАЛЕКО ПО ПОЛОЖИТЕЛЬНУЮ сторону, точки которые находятся "недалеко" от гиперплоскости берем с "заниженными" весами. Размер "НЕДАЛЕКО" регулируется как раз параметром s
Sig - берем точки ТОЛЬКО С ПОЛОЖИТЕЛЬНОЙ стороны, причем у всех таких точек будут одинаковые веса. Точки с отрицательной стороны не берем
TanH - очень похожа на Sigmoid, только точки которые далеко по отрицательную сторону гиперплоскости имеют вес ~-1.
Для Relu важен только знак параметра s. То есть для подобных функций нужно просто взять для половины выходов коэффициент равный s = +1 для другой s = -1. Тренировать этот коэффициент не нужно.
Дальше вспоминаем что перцептрон так же реализует логику OR/AND/AND_NOT.
То есть, если на первый слой смотреть в терминах Далеко/Близко от гиперплоскости или Берем по эту сторону/По другую не берем, а на следующий слой смотреть в терминах OR/AND/AND_NOT то мы примерно можем прочитать что делает нейросеть или наоборот ее построить.
Пример
Пусть у нас есть черный ящик. У черного ящика есть 2 входа и один выход. На выходе появляется всего 2 значения: 0 или 1.
Предположим мы знаем логику черного ящика, но все равно попытаемся ее «аппроксимировать» с помощью нейросети.
Истинная логика черного ящика простая - кольцо. Если входная точка попадает в кольцо - на выходе 1 (красный цвет) иначе 0 (белый);

Если строить минимальную рабочую нейросеть на обычных перцептронах - то нам достаточно будет 2х скрытых слоев, в первом будет 6 нейронов, во втором 2, и 1 нейрон в выходном слое:
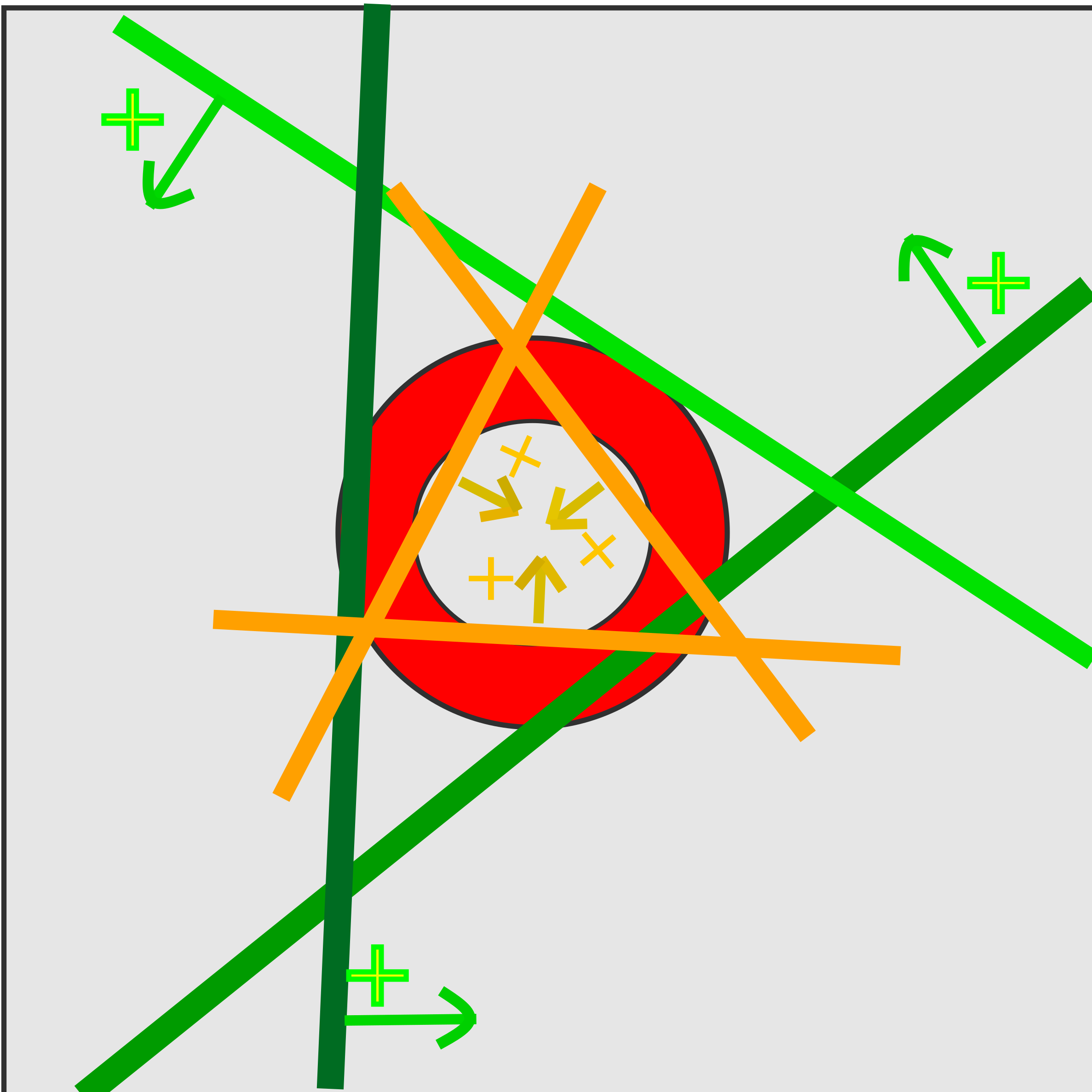
Интерпретация логики нейронной сети из обычных перцептронов получатся следующая:
Первый слой - каждый нейрон функция расстояния от линии (зеленого или оранжевого цвета), всего 6 таких.
Во втором слое первый нейрон (зеленый) реализует логику что точка находиться внутри зеленого треугольника.
То есть растояние от первой зеленой гипеплоскости положительно "И" от второй зеленой гиперплоскости положительно "И" от третей гиперплоскости положительно.
Второй нейрон второго слоя(оранжевый) - та же логика "И", но с оранжевыми треугольником.
Выходной нейрон реализует следующую логику: (точка внутри зеленого треугольника) and not (точка внутри оранжевого треугольника)
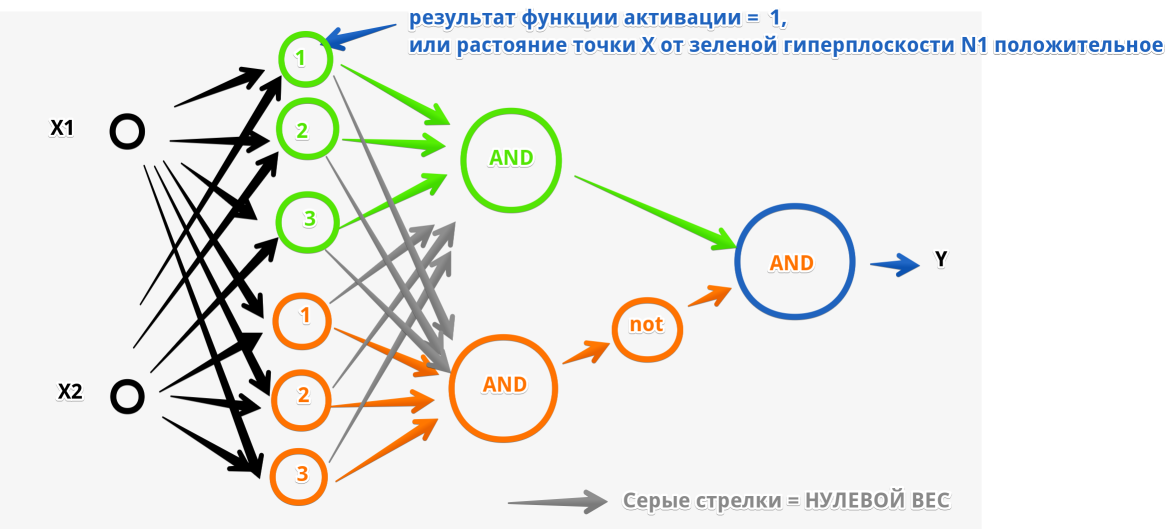
Небольшое доказательство/рассуждение что на одном нейроне можно построить логику A and NOT(B):
Если у нас функция активации предыдущего слоя Sigmoid - то выходные значения нейроном между 0 и 1. Отмечаем на плоскости красным точки когда выход должен быть равен нулю (красная точка) а когда единице (зеленая):
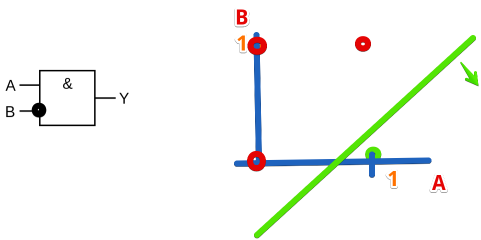
Видно что можно одной линией разделить пространство на две области, это может сделать один нейрон. Но так как из-за выбранной функции активации входное значение будет всегда меньше 1, а область которую нужно отделить является квадратом. Соответсвенно чтобы уменьшить погрешность лучше взять 2 нейрона вместо одного и добавить еще один скрытый слой.
Теперь, предположим, нам нужно увеличить точность получившейся нейронной сети.
Из рис 4 видно что точность достаточно сильно влияет 1й слой. Нам нужно больше нейронов, чтобы сделать "КРУГ" из гиперплоскостей более плавным.
Пусть теперь в первом скрытом слое будет 12 нейронов, во всех остальных слоях без изменений.
Теперь 6 нейронов используется для построения зеленой области, и 6 нейронов для построения оранжевой области:

Если внимательно присмотреться что происходит на последнем рисунке - видно что много линий ПОЧТИ параллельны друг другу.
Так же видно, что не важно под каким углом к системе координат расположены линии(в общем случае гиперплоскости). Их все можно повернуть на одинаковый градус, и точность от этого не измениться, потому что все что делают эти линии(гиперплоскости) «огораживают» нужную замкнутую область. И это как раз это позволяем нам тут воспользоваться "новым" нейроном с несколькими выходами. На рисунке ниже нарисованы гиперплоскости одного "нового" нейрона, с разными параметрами B и S :

То есть один "Новый" нейрон с 4мя выходами потенциально может заменить 4 обычных нейрона в первом скрытом слое. Новый нейрон может участвовать в "огораживании" сразу нескольких замкнутых областей.
Понятно что в зависимости от задачи эффективность нейронов с несколькими выходами будет разной, но если количество входов и выходов слоя достаточно большое - то однозначно нужно пробовать. Начинать стоит c n_surface_normal_reuse = 4.
Инициализация новых параметров
Есть мысли что на вектор нормали W лучше смотреть как на вектор длинной = 1 и инициализировать Wi равномерным распределением R(x | -1, 1) поделенным на (ΣWi2)0.5. Для смещения b - равномерным распределением b ∈ R(x | -(ΣMAX(|Xi|)2)0.5, (Σ(MAX(|Xi|))2)0.5), где max(|Xi|) - максимальное значение по модулю iго входа перцептрона.
В частном случае, если максимальные значения входов |Xi|=1 - то b ∈ R(0, N0.5).
Инициализация параметра s тоже похоже как-то зависит от Σ(MAX(|Xi|) и функции активации. Для Relu, как уже было сказано, это -1 или +1. Для семейства сигмойдных функций активаций - вопрос открытый.
Послесловие
Данная статья не является научной работой, и по сути является вопросом. Возможно где-то допущены ошибки и ложные утверждения/предположения, я надеюсь, знающие люди поправят.
Комментарии (15)

Hardcoin
11.08.2023 10:41+4Данная статья не является научной работой, и по сути является вопросом.
На вопрос не похоже, слишком длинно. Вы можете сделать нейросеть для MNIST с иллюстрацией вашей идеи? Покажете, насколько меньше стало параметров, это даст точку для старта.

nikolz
11.08.2023 10:41+2Если я Вас понял правильно, то вы два нейрона в слое заменяете одним с двумя выходами.
Но при этом Вы различные весовые коэффициенты каждого нейрона заменили на одинаковые от одного. В итоге Вы сократили число весовых коэффициентов на входах нейронов, так как вместо двух остался один нейрон.
Но я полагаю, что вы фактически просто обрезали сеть.
Сумма произведения весовых коэффициентов на входные сигналы, которая поступает на элемент сравнения нейрона представляет собой фильтр.
В исходной схеме таких фильтров два и они разные. Вы, выкинув один нейрон, выкинули один из фильтров. Все верно?
Всегда можно подобрать пример, в котором большинство слоев и нейронов в сети просто лишние. Но это недостаток примера, а не сети.
Нельзя ничего просто так обрезать ни на входе ни на выходе. Для этого есть процесс обучения и оптимизации структуры сети после обучения.

Alshug Автор
11.08.2023 10:41все верно пишите, уменьшаем количество фильтров. И в этом как раз заключается моя гипотеза: в некоторых задачах такой трюк может сработать и значительно сократить количество параметров. Эта же гипотеза с другого бока - можно увеличить точность сети небольшим увеличением кол-ва параметров. Поцесс обучения не меняется почти никак. Какие методы оптимизации вы имеете в виду?
Видел статью где полносвязный слой успешно заменяли CNN, что немного перекликается с перцептроном с несколькими выходами, но совсем разная интерпритация происходящего.

nikolz
11.08.2023 10:41+2Изложу свой подход к данному вопросу.
Изначально концепция нейронных сетей основана на том, что нам ничего неизвестно о среде, в которой сеть будет функционировать. Т е внешняя среда для сети изначально предполагается "черным ящиком".
Поэтому структура сети создается максимально обобщенной. Т е. задаем лишь исходные (доступные нам ) сигналы внешней среды , число слоев и число нейронов и предполагаем изначально, что "все соединяется со всем".
Т е сеть рождается без каких-либо знаний. Процесс обучения собственно и делается, чтобы сеть приобрела эти знания. В результате обучения может получиться, что, для выбранной нами среды существования сети, какие-то из нейронов и соединений будут избыточные. Тогда мы их уберем из сети.
Но проблема в том, что такая, изначально глупая, сеть будет очень долго обучаться.
Поэтому я сторонник сетей, в которых учитываются накопленные человеком знания о среде существования сети. Т е заменяем "черный" ящик на "серый".
Вы собственно это и делаете, но исходный посыл у Вас не от среды обитания сети, а от упрощения самой сети. т е Вы не от причины, а от следствия действуете, предполагая, что причина всегда есть. Упрощение сети - не цель, а лишь следствие.
Кроме того, я сторонник изначально не ограничивать в сети ни число нейронов ни число слоев. Т е в моей концепции сеть изначально состоит лишь из внешних сигналов и произвольного число нейронов и слоев.
Далее в процесс построения(обучения) сети вносятся ограничения, связанные с нашими априорные знаниями о среде существования сети.
Про оптимизацию сети...
Я сторонник эволюционных алгоритмов.
Например, Метод группового учёта аргументов (МГУА, автор Ивахненко А.Г.).
Возможно потому, что познакомился с МГУА , "когда мы были молодыми" по книге «Системы эвристической самоорганизации в технической кибернетике»
В качестве примера. В моей первой системе распознавания для технической диагностики изначально было 200 спектральных признаков, после обучения и оптимизации осталось три.

Alshug Автор
11.08.2023 10:41но исходный посыл у Вас не от среды обитания сети, а от упрощения самой сети
Название и посыл у меня немного клик-бейтные, это правда :)
Но, пожалуй, немного повторюсь, ибо считаю это важным. Хотя я в статье и написал про потенциальное уменьшение параметров многосвязного слоя(что вы приравниваете к упрощению), метод работает и в обратную сторону. Мы можем попробовать усложнить систему лишь незначительным увеличением кол-ва параметров.
У меня есть предчувствие что перцептрон с несколькими выходами очень хорошо сработает в большинстве задач, ибо полносвязные сети очень часто берут с очень большой избыточностью(по разным причинам). Но эксперименты пока времени проводить нет, подтвердить ничем не могу, потому статья везде с оговорками, и дисклеймер о том что это не является научной работой, а вопросом: "почему так никто не делает?"То есть к описываемому подходу нужно относиться именно как к очередному инструменту. Применять не применять - каждый решает сам.
>Кроме того, я сторонник изначально не ограничивать в сети ни число нейронов ни число слоев.
Значит вам 100% нужно попробовать этот подход в своих проектах. С небольшим увеличением кол-ва параметров вы получите большую сложность. Самое плохое что может случится - из 10 выходов нейрона будет использоваться всего один, и это будет работать как обычная сеть из перцептрона с одним выходом :)какие-то из нейронов и соединений будут избыточные. Тогда мы их уберем из сети.
Согласен что убрать перцептрон с несколькими выходами из сети сложнее. Это один из его минусов.
На перцептрон с несколькими выходами можно смотреть еще как на один из методов оптимизации. То есть, после того как сеть оттренирована и нужно ее подсушить, можно попробовать заменить обычный слой на слой с перцептронами с несколькими выходами.
nikolz
11.08.2023 10:41Вообще-то, мы с вами говорим о разном. Я говорю о нейронах,
а Вы о перцептронах. Нейрон имеет один выход,
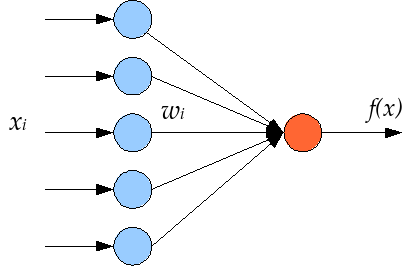
Схема искусственного нейрона — базового элемента любой нейронной сети а перцептрон - любое количество выходов. И их число не связано с сокращением количества входов или сокращением числа весовых коэффициентов.
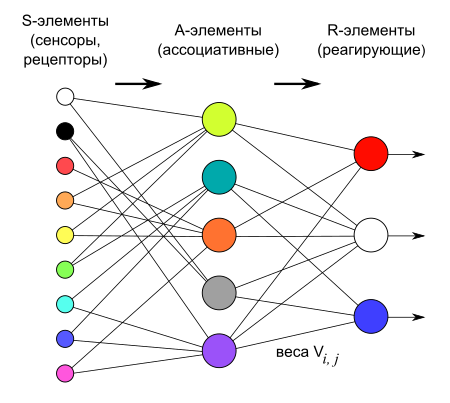
Логическая схема перцептрона с тремя выходами

VPryadchenko
11.08.2023 10:41И в этом как раз заключается моя гипотеза: в некоторых задачах такой трюк может сработать и значительно сократить количество параметров.
Все верно - персептроны как есть в реальных задачах не используются. Так, например, в картинках переход от персептрона к сверточной сети как раз есть способ сократить (причем, весьма существенно) число параметров за счет переиспользования весов.
В Вашем примере вообще достаточно двух нейронов с квадратичной функцией активации - один будет очерчивать внутреннюю, другой - наружную окружности. К чему я это - к тому, что конкретика зависит от задачи и, безусловно, может быть полезно закладывать в нее какое-то априорное знание о распределении данных. Но общим случаем был и остается персептрон как есть - без архитектурных оптимизаций.

azTotMD
11.08.2023 10:41+1Если я правильно понял схемы, то вы растиражировали выход из нейрона, после чего применили линейное преобразование к каждому экземпляру выхода. Получается все они зависимы, принципиально новой информации не возникает. Не уверен, что это даст пользу. Обычно стараются как раз сократить повторяющуюся информацию, оставив только разнородную.

Alshug Автор
11.08.2023 10:41я растирожиловал не выход нейрона а так называемый 'фильтр' он же вектор весов W. выходом нейрона является результат нелинейной фунции активации. При некоторых фунциях активации выходы могут быть зависимыми, но лишь на определенных отрезках, на всем дотупном пространстве входных параметров они независимы.

azTotMD
11.08.2023 10:41+1я растирожиловал не выход нейрона а так называемый 'фильтр' он же вектор весов W
никакой не вектор весов, а его поэлементное произведение на вход, да ещё и просуммированное (опять же если верить схеме). Т.е. это выход обычного нейрона за исключением отсутствующей функции активации и нулевого биаса. А потом вы из этого числа делаете 10 таких чисел и каждый пропускаете через линейное преобразование. Всё равно что за нейроном поставить полносвязанный слой, а после него активации воткнуть.

Alshug Автор
11.08.2023 10:41да, все верно пишете. Спасибо что на это указали, подумаю как поправить статейку чтобы было более понятно.
В моей голове нейрон без функции активации это не нейрон, как раз хотел подчеркнуть что полносвязный слой вставляется перед активацией

VDG
11.08.2023 10:41перепишем формулу обычного перцептрона
Перцептрон W*X + b считает скалярное произведение (косинус угла) между векторами W и X. Вы поделили это на магнитуду вектора W и перешли от углов к расстояниям — (W*X + b) / mag(W), а это уже что-то другое.
VPryadchenko
11.08.2023 10:41Ну не совсем так. Скалярное произведение - это не косинус угла в чистом виде, - там как раз модули обоих векторов есть в произведении. Поделив на модуль действительно перешли к расстояниям, но сути дела это не меняет: нормализация весов - вполне обыденная процедура. Идея автора, как я понял, в переиспользовании фильтров - тоже, в принципе, не нова, но надо отдать должное - автор вдумывается в суть происходящего, что, безусловно, хорошо.




VPryadchenko
А вопрос какой, я не понял, честно говоря?