 Привет, Хаброжители!
Привет, Хаброжители!Когда нужно, чтобы программа работала быстро и занимала поменьше памяти, профессионального программиста выручают знание алгоритмов и практика их применения. Эта книга — как раз про практику. Ее автор, Джордж Хайнеман, предлагает краткое, но четкое и последовательное описание основных алгоритмов, которые можно эффективно использовать в большинстве языков программирования. О том, какими методами решаются различные вычислительные задачи, стоит знать и разработчикам, и тестировщикам, и интеграторам.
Для кого эта книга
Предполагается, что читатель уже имеет практический опыт программирования — например, на Python. Если вы никогда не писали программ, я бы посоветовал сначала выучить какой-нибудь язык программирования, а потом уже браться за чтение. В книге используется Python, потому что он подходит и программистам, и непрограммистам.
Алгоритмы предназначены для решения общих задач, которые постоянно возникают при разработке программного обеспечения. Преподавая на младших курсах, я стараюсь навести мосты между знаниями студентов и понятиями, которые я использую в своих алгоритмах. Большинство учебников содержат тщательные пояснения, но все равно их всегда недостаточно. Частенько студент не может самостоятельно изучить алгоритм, потому что ему не показали, как ориентироваться в материале.
Я опишу цель этой книги одним абзацем и одной иллюстрацией. Начнем мы с нескольких структур данных, которые показывают, как информация представляется примитивными атомарными типами, например 32-разрядными целыми числами или 64-разрядными вещественными. Некоторые алгоритмы, в частности двоичный поиск, работают с такими структурами напрямую. Более сложные алгоритмы, например алгоритмы на графах, используют важные абстрактные типы данных (стек, приоритетная очередь и т. п.), которые мы изучим по ходу изложения. Абстрактный тип подразумевает набор действий над ним, и вот эти действия будут эффективны, только если выбрать подходящую структуру данных для его реализации. Ближе к концу книги мы рассмотрим, как повысить быстродействие различных алгоритмов. Сами алгоритмы мы либо целиком напишем на Python, либо рассмотрим соответствующие сторонние пакеты Python, в которых они эффективно реализованы.
Если вы заглянете в сопутствующие книге исходные тексты программ, то найдете там в каждой главе файл book.py — это программа на Python, которая при запуске воспроизводит на вашем компьютере все схемы из книги (рис. В.1).
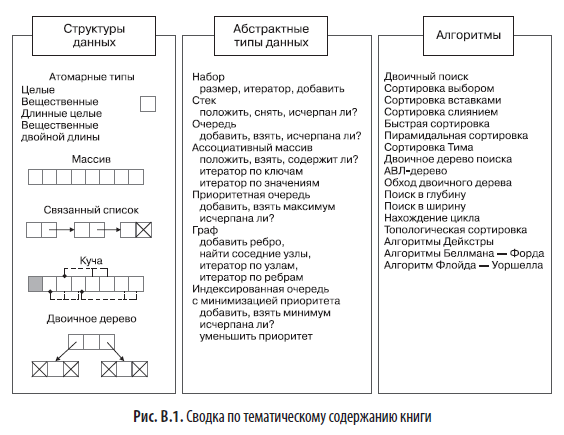
В конце каждой главы есть проверочные упражнения, на них вы можете потренироваться применять свежие знания. Очень советую сначала попробовать решить задачи самостоятельно, а потом сравнить с примерами решений в репозитории к книге.
Алгоритмы предназначены для решения общих задач, которые постоянно возникают при разработке программного обеспечения. Преподавая на младших курсах, я стараюсь навести мосты между знаниями студентов и понятиями, которые я использую в своих алгоритмах. Большинство учебников содержат тщательные пояснения, но все равно их всегда недостаточно. Частенько студент не может самостоятельно изучить алгоритм, потому что ему не показали, как ориентироваться в материале.
Я опишу цель этой книги одним абзацем и одной иллюстрацией. Начнем мы с нескольких структур данных, которые показывают, как информация представляется примитивными атомарными типами, например 32-разрядными целыми числами или 64-разрядными вещественными. Некоторые алгоритмы, в частности двоичный поиск, работают с такими структурами напрямую. Более сложные алгоритмы, например алгоритмы на графах, используют важные абстрактные типы данных (стек, приоритетная очередь и т. п.), которые мы изучим по ходу изложения. Абстрактный тип подразумевает набор действий над ним, и вот эти действия будут эффективны, только если выбрать подходящую структуру данных для его реализации. Ближе к концу книги мы рассмотрим, как повысить быстродействие различных алгоритмов. Сами алгоритмы мы либо целиком напишем на Python, либо рассмотрим соответствующие сторонние пакеты Python, в которых они эффективно реализованы.
Если вы заглянете в сопутствующие книге исходные тексты программ, то найдете там в каждой главе файл book.py — это программа на Python, которая при запуске воспроизводит на вашем компьютере все схемы из книги (рис. В.1).

В конце каждой главы есть проверочные упражнения, на них вы можете потренироваться применять свежие знания. Очень советую сначала попробовать решить задачи самостоятельно, а потом сравнить с примерами решений в репозитории к книге.
Соответствие значений ключам
Часто набор объектов, которые нужно уметь хранить в памяти, представлен не в виде последовательности, а в виде множества пар (ключ, значение), в котором каждому ключу однозначно соответствует некоторое значение. Такая структура называется ассоциативным массивом. Если наложить дополнительные требования на свойство ключа, вместо поиска пары (ключ, значение) по всему набору можно использовать гораздо более эффективный прием — хеширование. Поиск по хешу работает быстрее любого изученного нами алгоритма поиска! Ассоциативный массив сохраняет эффективность, даже если разрешить удаление ключей и значений. Порядок следования ключей в такой структуре определяется ее реализацией (в словарях Python ключи идут в порядке добавления, в устаревшем Python2 определенный порядок не гарантировался вовсе; в любом случае ключи почти наверняка не будут упорядочены по возрастанию, как индексы массива). Взамен мы получаем великолепную скорость поиска и добавления пары.
Скажем, мы хотим написать функцию print_month(month, year), которая будет выводить календарь на определенный месяц определенного года. С параметрами print_month('February', 2024) функция должна выводить примерно это:

Что нам нужно для этого знать? День недели, с которого в этом году начинается месяц (в примере это четверг), а еще — сколько дней в феврале этого года (28, а если год високосный, как 2024-й, то 29). Для количества дней в месяце заведем числовой массив, каждый элемент которого будет соответствовать месяцу, начиная с января:
month_length = 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31Итак, в январе 31 день, поэтому month_length[0] == 31, в феврале — 28, так что следующее значение — 28 и т. д. до последнего 31, которое соответствует 31 дню в декабре.
Изученные нами ранее примеры позволяют предположить, что понадобится также массив той же длины с названиями месяцев — ключей, по которым мы сможем определить, по какому индексу в month_length находится искомое количество дней. Вот такой фрагмент программы выводит количество дней в феврале:
key_array = ('Январь', 'Февраль', 'Март', 'Апрель', 'Май', 'Июнь', 'Июль',
'Август', 'Сентябрь', 'Октябрь', 'Ноябрь', 'Декабрь')
idx = key_array.index('Февраль')
print('В феврале', month_length[idx], 'дней')Если название месяца в массиве ключей есть, этот фрагмент будет работать. Однако в худшем случае, когда нам нужен 'Декабрь', придется просмотреть все значения. Если ключа в массиве нет, key_array.index() выдаст исключение, так что предварительно нам придется проверить наличие ключа, например, с помощью key in key_array. Это тоже худший случай, потому что будут просмотрены все строки в key_array. Следовательно, время поиска значения по ключу в изобретенной нами структуре прямо пропорционально количеству ключей. Такая скорость поиска довольно быстро станет медленной до полной неприемлемости. Несмотря на это, давайте все-таки напишем print_month(). В частности, в примере 3.1 приведена возможная реализация, в которой задействованы два стандартных модуля Python — datetime (для определения дня недели) и calendar (для определения високосного года).
Пример 3.1. Вывод на экран календаря за произвольный год и месяц в удобном формате
from datetime import date
import calendar
month_length = 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
key_array = ('Январь', 'Февраль', 'Март', 'Апрель', 'Май', 'Июнь', 'Июль',
'Август', 'Сентябрь', 'Октябрь', 'Ноябрь', 'Декабрь')
def print_month(month, year):
idx = key_array.index(month) ❶
wd = date(year, idx + 1, 1).weekday() ➋
days = month_length[idx] ❸
if calendar.isleap(year) and idx == 1: ❹
days += 1
print(f"{month} {year}".center(20))
print("Пн Вт Ср Чт Пт Сб Вс")
print(' ' * wd, end='') ❺
for day in range(days):
wd = (wd + 1) % 7 ❻
eow = " " if wd % 7 else "\n" ❼
print(f"{day+1:2}", end=eow)
print()❶ Найдем номер месяца (целое число от 0 до 11) — индекс в month_length.
➋ Вычислим первый день недели данного месяца в данном году, 0 — это понедельник. В функцию date() передается idx + 1, потому что месяцы в ней нумеруются с единицы, а не с нуля.
❸ Определим количество дней в месяце.
❹ В високосном году в феврале 29 дней (мы нумеруем месяцы с нуля, так что февраль — это 1).
❺ Вместо дней прошедшего месяца в первой неделе выведем пробелы, тогда первый день окажется на своем месте.
❻ Вычислим следующий день недели.
❼ Вычислим, что выводить после текущей даты. Если следующий день не понедельник, то есть wd не делится на 7, нужно выводить пробел, а если понедельник — конец строки, потому что неделя закончилась.
Чтобы оценить производительность поиска ключа в наборе из N пар (ключ, значение), имеет смысл посчитать количество операций индексирования. Функция key_array.index() для поиска нужной строки может просматривать вплоть до N элементов, так что ее сложность — O(N).
Тип данных list реализован в Python как динамический массив, размер которого может меняться. Для краткости его часто называют просто списком. В этой главе мы также будем использовать термин «массив» в знак того, что наши методы применимы и к классическим массивам неизменяемой длины. Кроме того, если мы не собираемся менять и сами элементы массива, в программах на Python лучше использовать кортежи (тип данных tuple), как в примерах выше.
Ассоциативные массивы, хранящие произвольные значения по ключу, реализованы в Python специальным типом данных dict (от dictionary — «словарь»). Мы можем составить словарь days_in_month, хранящий целые числа — продолжительность месяцев в днях в соответствии с ключами — названиями месяцев (с заглавной буквы):
days_in_month = {'Январь': 31, 'Февраль': 28, 'Март': 31,
'Апрель': 30, 'Май': 31, 'Июнь': 30,
'Июль': 31, 'Август': 31, 'Сентябрь': 30,
'Октябрь': 31, 'Ноябрь': 30, 'Декабрь': 31 }А вот пример вывода утверждения «в апреле 30 дней»:
print('В апреле', days_in_month['Апрель'], 'дней')В словаре на поиск ключа в среднем уходит O(1) времени, независимо от количества хранящихся в нем пар (ключ, значение). Совершенно удивительный результат, будто фокусник только что достал кролика из шляпы! Словарями мы воспользуемся в восьмой главе, а пока попробуем сами достать этого кролика. Пример ниже предлагает интуитивное описание математического механизма, который мы изучаем в этой главе. Смысл в том, чтобы для начала преобразовать строку в число.
Будем считать, что буква «а» — это 0, буква «б» — 1 и т. д. до «я» — 31. С помощью этих 32 «цифр» любое русское слово (увы, без буквы «е»), записанное строчными буквами, соответствует некоторому числу в системе счисления с основанием 32. Например, в «числе» «июнь» четыре цифры — «и», «ю», «н» и «ь». Если начать переводить из тридцатидвоичной системы счисления в привычную нам десятичную, получится «и» × 323 + «ю» × 322 + «н» × 321 + «ь» × 320, или, после вынесения основания за скобки, 32 × (32 × (32 × «и» + «ю») + «н») + «ь». Именно так и работает функция base32() в примере 3.2.
Пример 3.2. Интерпретация слова как числа с основанием 32
def base32(w):
val = 0
for ch in w.lower(): ❶
next_digit = ord(ch) - ord('а') ➋
val = 32 * val + next_digit ❸
return val❶ Преобразуем буквы строки в строчные.
➋ Вычислим значение очередной цифры.
❸ Припишем цифру в конец результата.
В base32() используется функция ord(), которая возвращает порядковый номер буквы в таблице всех известных Python символов Unicode. Буквы от «а» до «я» идут в алфавитном порядке, ord('а') == 1072, ord('б') == 1073 и т. д. до ord('я') == 1103. Так что для того, чтобы вычислить значение «и», достаточно вычесть порядковые номера: ord('и') — ord('а') — и получить 8.
Значение base32() очень быстро растет с ростом длины строки. Уже base32('Июнь') возвращает 293308, а base32('Сентябрь') — так и вовсе 589940360732.
Как бы такие большие числа втиснуть в более приемлемый диапазон? Можно применить операцию «остаток от деления»: в Python, как и во многих языках программирования, это %. Остаток сколь угодно большого целого числа (например, base32(month)) можно взять относительно достаточно малого делителя.
Немного поэкспериментировав, мы можем обнаружить, что для всех названий месяцев значения base32(month) % 35 различны. Например, base32('Август') равно 2215474, а 2215474 % 35 == 9, и для каждого месяца результат будет иным. Теперь, как показано на рис. 3.1, мы можем завести массив на 35 элементов, с помощью которого можно узнать количество дней в данном месяце, за одно обращение, и перебирать все пары (ключ, значение) не нужно. Вычисляем формулу для февраля, получаем 0, на нулевой позиции в day_array стоит 28 — в феврале 28 дней. Проделываем то же самое с ноябрем — получаем позицию 32 и 30 дней.
Давайте еще раз оценим, что у нас получилось. Вместо цикла по всем ключам в массиве нам нужно проделать несложное преобразование самого ключа, которое даст позицию нужного значения в массиве. Время нашего вычисления зависит от длины ключа, но не зависит от общего количества ключей — это очень большой шаг вперед!
base32('Февраль') % 35 == 0 // Нулевой элемент равен 28
day_array = (
28, -1, 30, -1, -1, -1, -1,
-1, 30, 31, -1, -1, 31, -1,
31, 31, -1, -1, 30, -1, -1,
31, -1, -1, -1, -1, 31, -1,
-1, -1, -1, 31, 30, -1, -1
)
base32('Ноябрь') % 35 == 32 // 32-й элемент равен 30
Поработать, правда, пришлось изрядно. Во-первых, подыскать формулу однозначного преобразования имени месяца в индекс, а во-вторых, создать массив на 35 элементов, из которых имеет смысл только дюжина, а значит, больше половины этого массива потрачено впустую. В нашем примере объем хранимых данных N равен 12, а объем хранилища M — 35.
Если для некоторой строки s элемент day_array в позиции base32(s) % 35 равен -1, очевидно, эта строка не название месяца. Этим удобно пользоваться. Может показаться, что если day_array[base32(s)%35] > 0, то любая строка s — допустимое название месяца, но это, конечно, не так. К примеру, base32(«Промахнулось») выдает то же самое, что и base32(«Февраль»); получится, что «Промахнулось» — это такой месяц и в нем 28 дней! Это довольно неприятное свойство, и нам придется разобраться, как с ним справиться.
Хеш-функции и хеш-суммы
Формула base32(s) % 35 — пример хеш-функции, которая отображает ключ произвольного размера в хеш-сумму (или просто хеш) в заданном диапазоне значений. В нашем примере хеш не меньше нуля и не больше 34. Множество хеш-функций возвращают произвольное 32-разрядное целое (в диапазоне от –2 147 483 648 до 2 147 483 647) или произвольное 64-разрядное целое (в диапазоне от –9 223 372 036 854 775 808 до 9 223 372 036 854 775 807). Нетрудно заметить, что хеши бывают и отрицательными.
Задача отображения структурированных данных в фиксированные целые числа, то есть задача отыскания подходящей хеш-функции, занимает математиков последние несколько десятилетий. Программисты пользуются плодами их трудов: большинство языков программирования включают в себя вычисление хеша произвольного набора данных. В Python функция hash() для неизменяемых объектов встроена в сам язык.
Единственное обязательное свойство хеш-функции — однозначность. Хеш, посчитанный от двух одинаковых объектов, должен совпадать; нельзя каждый раз брать первое попавшееся число. Хеш неизменяемого объекта (например, string в Python) можно вычислять лишь единожды и потом хранить — это снизит общее количество вычислений.
Хеш-функция не обязана для каждого ключа давать уникальное число, не равное другим значениям функции (впрочем, в конце главы мы рассмотрим идеальные хеши, которые это умеют). Более того, ценой еще большей неуникальности мы можем резко уменьшить диапазон ее значений до 0… M – 1: возьмем остаток от деления на M.
В табл. 3.1 представлено 32-разрядное значение функции hash() для некоторых строк и соответствующий им остаток от деления на 15. Формула hash(key) % 15 обладает свойством однозначности, но если с точки зрения теории вероятности шанс на совпадение значений hash() у двух ключей исчезающе мал, то на малом диапазоне совпадение хешей вполне вероятно. В нашем примере таких совпадений два: «рифмы» — «возьми» со значением 10 и «ее» — «скорей» со значением 3. Несмотря на различие вероятностей, всегда стоит ожидать, что две разные строки могут иметь одинаковый хеш.
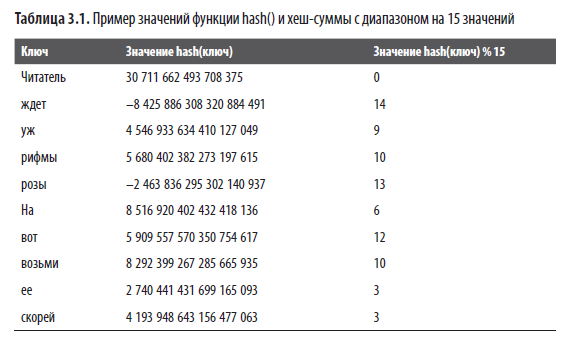
Если использовать остаток от деления на M для того, чтобы вычислить хеш, hash(key) % M, стоит озаботиться тем, чтобы диапазон оказался не меньше, чем общее количество ключей.
Лет десять назад в Python (а в Java — до сих пор) встроенная функция hash() стабильно возвращала один и тот же конкретный хеш для каждого конкретного параметра. В современном Python в значения хешей при запуске интерпретатора подмешивается соль — независимое случайное значение. В течение работы одного процесса Python соль не меняется, но предсказать ее значение для очередного запуска интерпретатора невозможно — это повышает безопасность приложений. Если хеш предсказуем, хакер может наполнить словарь заранее просчитанными ключами с одинаковым хешем. Это нарушит равномерность их распределения в хеш-таблице, и производительность словаря упадет до O(N). Таким способом можно организовать так называемую DoS-атаку (от Denial of Service — «отказ в обслуживании»).
Больше информации относительно «подсоленного хеша» можно найти по ссылке oreil.ly/C4V0W и в Python-документации PEP 456. Кроме того, в конце главы есть упражнение на эту тему.
Хеш-таблица: хранение данных по ключу
Для удобства работы заведем отдельный тип данных для пары (ключ, значение):
class Entry:
def __init__(self, k, v):
self.key = k
self.value = vВ примере 3.3 определен класс Hashtable, внутри которого в массиве table может храниться не более M объектов. Каждая из M позиций массива table — ячейка хеш-таблицы (по-английски bucket — «ведро» или «корзина»). Для начала определим, что каждая ячейка либо пуста, либо хранит ровно одну пару (объект типа Entry).
Пример 3.3. Неэффективная реализация хеш-таблицы
class Hashtable:
def __init__(self, M=10):
self.table = [None] * M ❶
self.M = M
def get(self, k): ➋
hc = hash(k) % self.M
return self.table[hc].value if self.table[hc] else None
def put(self, k, v): ❸
hc = hash(k) % self.M
entry = self.table[hc]
if entry:
if entry.key == k:
entry.value = v
else: ❹
raise RuntimeError(f'Key Collision: {k} and {entry.key}')
else:
self.table[hc] = Entry(k, v)❶ Заводим массив на M объектов.
➋ Метод .get() определяет номер ячейки по ключу k, для которого вычисляется хеш, и возвращает значение, если оно есть.
❸ Метод .put() определяет номер ячейки по ключу k, для которого вычисляется хеш, и перезаписывает хранящееся там значение — или записывает новое, если ячейка была пуста.
❹ Если хеш двух различных ключей приводит к одной и той же ячейке — это коллизия, происходит исключение.
Вот так нашей хеш-таблицей можно пользоваться:
table = Hashtable(1000)
table.put('Апрель', 30)
table.put('Май', 31)
table.put('Сентябрь', 30)
print(table.get('Август')) # Промах: должно быть выведено None
print(table.get('Сентябрь')) # Попадание: должно быть выведено 30Если все работает как задумано, значит, в массиве на 1000 элементов нам удалось разместить три пары — объекты типа Entry. Скорость работы .put() и .get() не зависит от количества пар в таблице, так что их быстродействие можно оценить как O(1).
Если .get(key) не находит key в соответствующей хешу ячейке — это промах. Если .get(key) выбрал ячейку по хешу и ключ находящейся там пары равен key — это попадание. В таких случаях хеш-таблица работает так, как предполагается. Чего нам пока не хватает — это поведения на случай коллизии хеша, когда два или больше ключа имеют одинаковый хеш. Если не обрабатывать коллизии, метод .put(ключ) начнет удалять содержимое непустых ячеек, хеш ключа которых совпадает с хешем нового ключа. Смысла в хеше Hashtable, который теряет ключи, нет.
Об авторе
Джордж Хайнеман — профессор computer science с более чем 20-летним стажем разработки программного обеспечения и исследования эффективности алгоритмов. Хайнеман — автор книги Algorithms in a Nutshell и множества учебных курсов O’Reilly, таких как Exploring Algorithms in Python («Исследование алгоритмов на языке Python») и Working with Algorithms in Python («Работа с алгоритмами на языке Python»). С давних пор он интересуется логическими и математическими головоломками и даже изобрел несколько, например Sujiken® (вариант судоку) и Trexagon.
Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Алгоритмы

