О чём статья
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
l1 = 1/(1+np.exp(-(np.dot(X,syn0))))
l2 = 1/(1+np.exp(-(np.dot(l1,syn1))))
l2_delta = (y - l2)*(l2*(1-l2))
l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))
syn1 += l1.T.dot(l2_delta)
syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np
# Сигмоида
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
# набор входных данных
X = np.array([ [0,0,1],
[0,1,1],
[1,0,1],
[1,1,1] ])
# выходные данные
y = np.array([[0,0,1,1]]).T
# сделаем случайные числа более определёнными
np.random.seed(1)
# инициализируем веса случайным образом со средним 0
syn0 = 2*np.random.random((3,1)) - 1
for iter in xrange(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0,syn0))
# насколько мы ошиблись?
l1_error = y - l1
# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1,True) # !!!
# обновим веса
syn0 += np.dot(l0.T,l1_delta) # !!!
print "Выходные данные после тренировки:"
print l1
Выходные данные после тренировки:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
"*" — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
"-" – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
И это работает! Рекомендую перед прочтением объяснения поиграться немного с кодом и понять, как он работает. Он должен запускаться прямо как есть, в ipython notebook. С чем можно повозиться в коде:
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена !!!)
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена !!!)
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
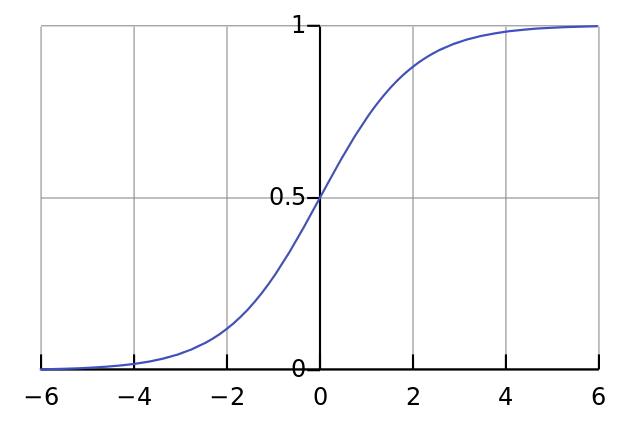
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. ".T" – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним. Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.
Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода.
l1_error = y - l1
Поскольку в l1 содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l1 из правильного ответа y. l1_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.
l1_delta = l1_error * nonlin(l1,True)
А вот и секретный ингредиент. Эту строку нужно разбирать по частям.
Первая часть: производная
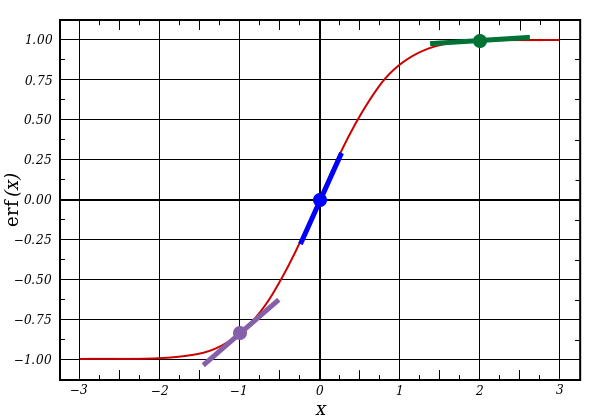
nonlin(l1,True)
l1 представляет три этих точки, а код выдаёт наклон линий, показанных ниже. Заметьте, что при больших значениях вроде x=2.0 (зелёная точка) и очень малые, вроде x=-1.0 (фиолетовая) линии имеют небольшой уклон. Самый большой угол у точки х=0 (голубая). Это имеет большое значение. Также отметьте, что все производные лежат в пределах от 0 до 1.
Полное выражение: производная, взвешенная по ошибкам
l1_delta = l1_error * nonlin(l1,True)
Математически существуют более точные способы, но в нашем случае подходит и этот. l1_error – это матрица (4,1). nonlin(l1,True) возвращает матрицу (4,1). Здесь мы поэлементно их перемножаем, и на выходе тоже получаем матрицу (4,1), l1_delta.
Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если наклон линии был небольшим, то в сети содержится либо очень большое, либо очень малое значение. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю.
syn0 += np.dot(l0.T,l1_delta)
Мы готовы к обновлению сети. Рассмотрим один тренировочный пример. В нём мы будем обновлять веса. Обновим крайний левый вес (9.5)
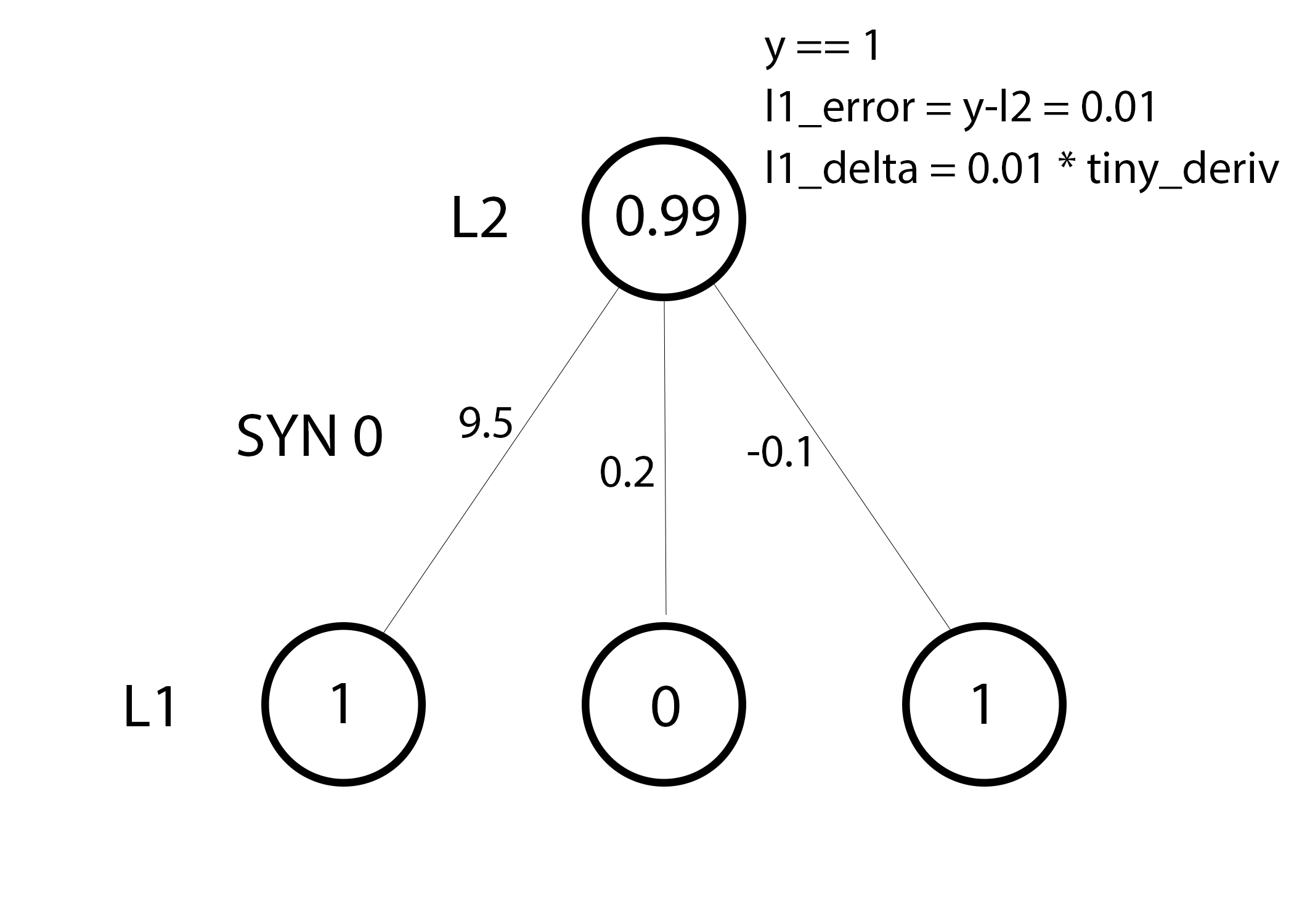
weight_update = input_value * l1_delta
Для крайнего левого веса это будет 1.0 * l1_delta. Предположительно, это лишь незначительно увеличит 9.5. Почему? Поскольку предсказание было уже достаточно уверенным, и предсказания были практически правильными. Небольшая ошибка и небольшой наклон линии означает очень небольшое обновление.
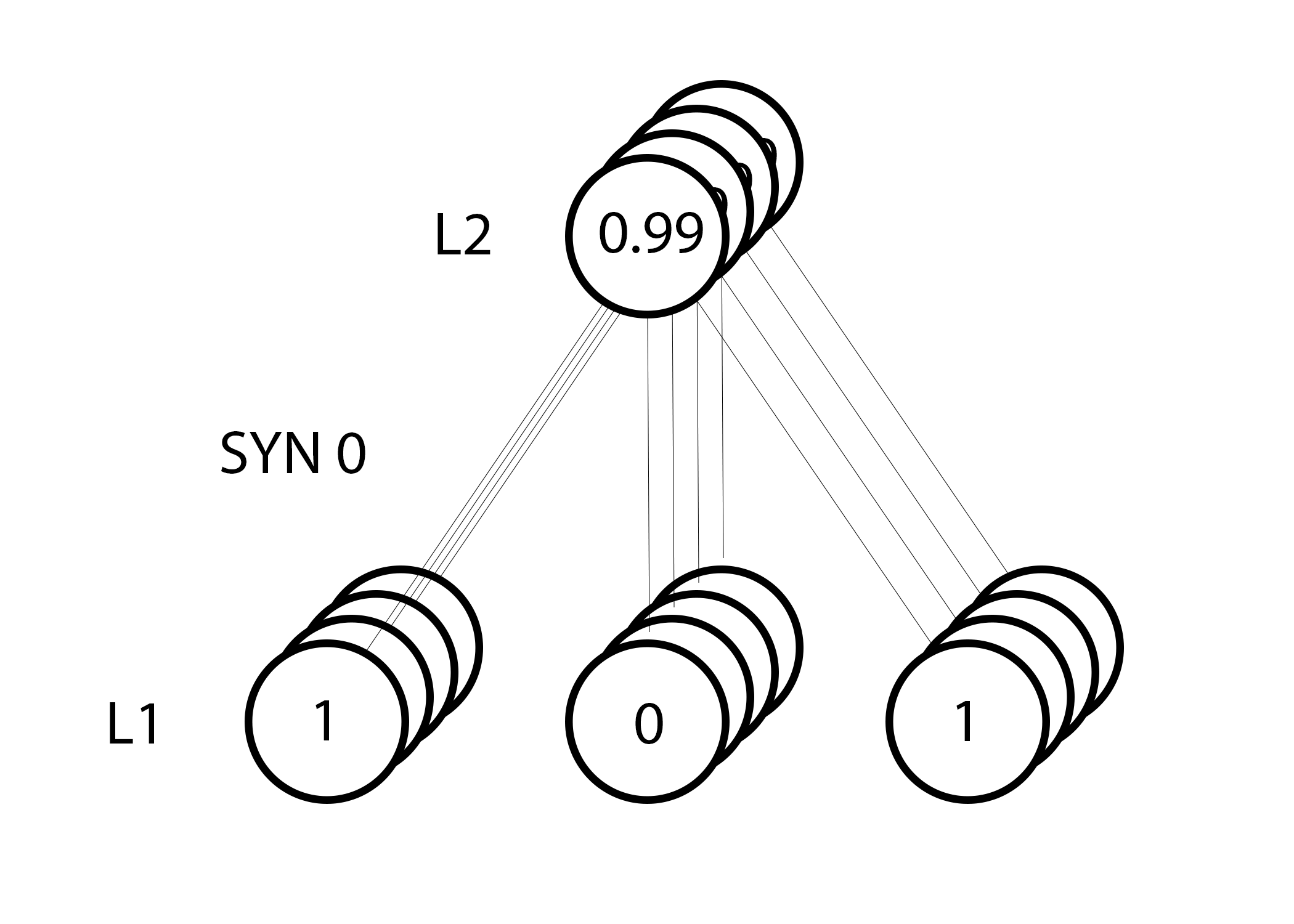
Но поскольку мы делаем групповую тренировку, указанный выше шаг мы повторяем для всех четырёх тренировочных примеров. Так что это выглядит очень похоже на изображение вверху. Так что же делает наша строчка? Она подсчитывает обновления весов для каждого веса, для каждого тренировочного примера, суммирует их и обновляет все веса – и всё одной строкой.
Понаблюдав за обновлением сети, вернёмся к нашим тренировочным данным. Когда и вход, и выход равны 1, мы увеличиваем вес между ними. Когда вход 1, а выход – 0, мы уменьшаем вес.
Вход Выход
0 0 1 0
1 1 1 1
1 0 1 1
0 1 1 0
Таким образом, в наших четырёх тренировочных примерах ниже, вес первого входа по отношению к выходу будет постоянно увеличиваться или оставаться постоянным, а два других веса будут увеличиваться и уменьшаться в зависимости от примеров. Этот эффект и способствует обучению сети на основе корреляций входных и выходных данных.
Часть 2: задачка посложнее
Вход Выход
0 0 1 0
0 1 1 1
1 0 1 1
1 1 1 0
Попробуем предсказать выходные данные на основе трёх входных столбцов данных. Ни один из входных столбцов не коррелирует на 100% с выходным. Третий столбец вообще ни с чем не связан, поскольку в нём всю дорогу содержатся единицы. Однако и тут можно увидеть схему – если в одном из двух первых столбцов (но не в обоих сразу) содержится 1, то результат также будет равен 1.
Это нелинейная схема, поскольку прямого соответствия столбцов один к одному не существует. Соответствие строится на комбинации входных данных, столбцов 1 и 2.
Интересно, что распознавание образов является очень похожей задачей. Если у вас есть 100 картинок одинакового размера, на которых изображены велосипеды и курительные трубки, присутствие на них определённых пикселей в определённых местах не коррелирует напрямую с наличием на изображении велосипеда или трубки. Статистически их цвет может казаться случайным. Но некоторые комбинации пикселей не случайны – те, что формируют изображение велосипеда (или трубки).

Стратегия
Чтобы скомбинировать пиксели в нечто, у чего может появиться однозначное соответствие с выходными данными, нужно добавить ещё один слой. Первый слой комбинирует вход, второй назначает соответствие выходу, используя в качестве входных данных выходные данные первого слоя. Обратите внимание на таблицу.
Вход (l0) Скрытые веса (l1) Выход (l2)
0 0 1 0.1 0.2 0.5 0.2 0
0 1 1 0.2 0.6 0.7 0.1 1
1 0 1 0.3 0.2 0.3 0.9 1
1 1 1 0.2 0.1 0.3 0.8 0
Случайным образом назначив веса, мы получим скрытые значения для слоя №1. Интересно, что у второго столбца скрытых весов уже есть небольшая корреляция с выходом. Не идеальная, но есть. И это тоже является важной частью процесса тренировки сети. Тренировка будет только усиливать эту корреляцию. Она будет обновлять syn1, чтобы назначить её соответствие выходным данным, и syn0, чтобы лучше получать данные со входа.
Нейросеть в три слоя
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True):
return x*(1-x)
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0],
[1],
[1],
[0]])
np.random.seed(1)
# случайно инициализируем веса, в среднем - 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# проходим вперёд по слоям 0, 1 и 2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# как сильно мы ошиблись относительно нужной величины?
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
# в какую сторону нужно двигаться?
# если мы были уверены в предсказании, то сильно менять его не надо
l2_delta = l2_error*nonlin(l2,deriv=True)
# как сильно значения l1 влияют на ошибки в l2?
l1_error = l2_delta.dot(syn1.T)
# в каком направлении нужно двигаться, чтобы прийти к l1?
# если мы были уверены в предсказании, то сильно менять его не надо
l1_delta = l1_error * nonlin(l1,deriv=True)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Переменные и их описания
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
l2 – финальный слой, это наша гипотеза. По мере тренировки должен приближаться к правильному ответу
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
syn1 – второй слой весов, Synapse 1, объединяет l1 с l2.
l2_error – промах сети в количественном выражении
l2_delta – ошибка сети, в зависимости от уверенности предсказания. Почти совпадает с ошибкой, за исключением уверенных предсказаний
l1_error – взвешивая l2_delta весами из syn1, мы подсчитываем ошибку в среднем/скрытом слое
l1_delta – ошибки сети из l1, масштабируемые по увеернности предсказаний. Почти совпадает с l1_error, за исключением уверенных предсказаний
Код должен быть достаточно понятным – это просто предыдущая реализация сети, сложенная в два слоя один над другим. Выход первого слоя l1 – это вход второго слоя. Что-то новое есть лишь в следующей строке.
l1_error = l2_delta.dot(syn1.T)
Использует ошибки, взвешенные по уверенности предсказаний из l2, чтобы подсчитать ошибку для l1. Получаем, можно сказать, ошибку, взвешенную по вкладам – мы подсчитываем, какой вклад в ошибки в l2 вносят значения в узлах l1. Этот шаг и называется обратным распространением ошибок. Затем мы обновляем syn0, используя тот же алгоритм, что и в варианте с нейросетью из двух слоёв.
Комментарии (10)

middle
24.11.2015 16:38+2В вашем коде не хватает пробелов. Я могу поделиться своими:
* *

AndersonDunai
25.11.2015 03:42-4В вашем комментарии не хватает блоков «source», держите!
<source></source>
Хотя проблемму это все же не решит…

teleavtomatika
25.11.2015 00:33-3Вот это сюрприз, это получается, что в питоне продолжительность блока for табуляцией что-ли регулируется? А где блок закончится в этом случае:
for():
--xxxxx
--xxxxx
xxxxx
--xxxxx
?masai
25.11.2015 01:20+10Блок будет ограничен второй и третьей строками. А на пятой парсер выдаст ошибку (если конечно, в четвертой снова не начинается цикл, условный оператор, список и т. п.)
Настоящий сюрприз в том, что кто-то ещё удивляется языкам со значимыми отступами.
teleavtomatika
25.11.2015 03:03+9Я вырос в мире C и, честно говоря, ни разу мне еще не приходилось сталкиваться с языками в которых используются значимые отступы. (java, php, js, ael, c, c#, c++, vb, perl — дальше я особо не лезу).
Судя по реакции на предыдущий мой комментарий, каждого удивленного щедро одаривают минусами. Спасибо, я исправлюсь.
AndersonDunai
25.11.2015 03:37+5Я тоже сишник, но пишу уже несколько лет на Python'е и перед тем, как спросить, посмотрю в интернете, нет ли там ответа на мой вопрос. А минусы вы получили, полагаю, из-за того, что спросили довольно очевидную для многих глупость, не посмотрев в гугле хотя бы результаты по запросу «python tabulation.» Минус являет собой голос в пользу намека на неконструктивность комментария. Это не личный наезд или унижение, а просто общественное мнение.
Aclz
25.11.2015 07:14-6каждого удивленного щедро одаривают минусами
Только каждого удивленного всем известной банальностью, еще и не поленившегося заявить об этом открытии Америки во всеуслышанье.


domix32
Тогда в 12 ибо без
import numpy as npоно не будет работать