7. Точность систем автоматического регулирования (ч.1) / forpes.ru

Главная
7. Точность систем автоматического регулирования (ч.1)

7. Точность систем автоматического регулирования (ч.1) +10

11.09.2023 21:44

petuhoff 5 2100 Источник

7.1 Общие понятия о точности процесса управления

Как отмечалось в разделе 6, интегральная оценка управления складывается из 3-х основных понятий:

устойчивость САР;
точность САР;
качество переходного процесса.

Очевидно, что главным является устойчивость САР (или запас устойчивости). Если САР не устойчива или очень мал запас устойчивости, то говорить о точности (неустойчивая САР) или о качестве переходного процесса (малые запасы устойчивости) не имеет смысла.

Если САР устойчива и запасы устойчивости достаточны по величине, то понятие точность САР является весьма важным показателем.

Точность определяют по отработке САР следующих видов воздействий:

ступенчатое внешнее воздействие (управляющее или возмущающее) часто называется постоянным внешним воздействием;
линейное внешнее воздействие т.е. линейно изменяющееся внешнее воздействие (управляющее или возмущающее);
гармоническое воздействие, т.е. ;
медленно меняющееся произвольное внешнее (управляющее или возмущающее) воздействие;
другие воздействия (параболическое, импульсное и т.д.).

Наиболее часто для оценки точности САР используются постоянное (ступенчатое) и линейное воздействия.

Различают статические и астатические САР:

Рисунок 7.1.1 Переходные процессы статической и астатической САР

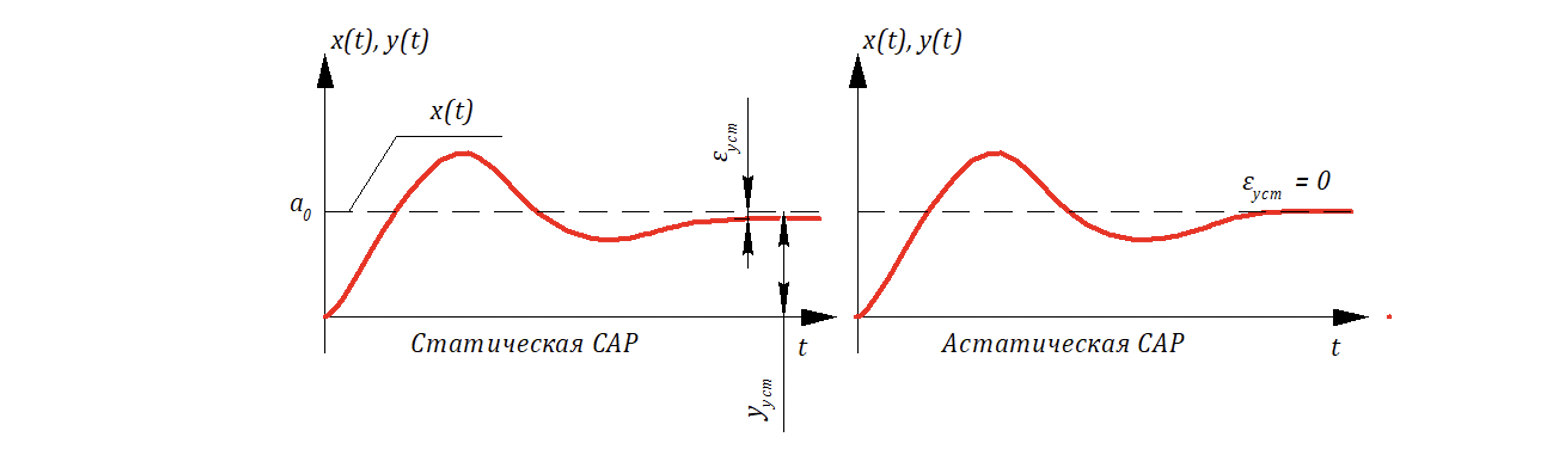
Данные графики будем относить к следующей структуре САР:

Рисунок 7.1.2 Струкутурная схема САР для анализа устойчивости

По установившейся ошибкой понимают:

$\varepsilon _{уст.}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Если входное воздействие - ступенчатое, to $\varepsilon_{уст.}$ - "постоянная" ошибка.

Если входное воздействие - линейное, to $\varepsilon_{уст.}$ - "скоростная" ошибка.

Различают астатизм по управляющему воздействию, а также астатизм по возмущающему воздействию, причем наличие того или иного астатизма определяется по-разному (см. следующие подразделы).

Главной задачей системы автоматического регулирования является точная и быстрая (но плавная) отработка управляющих воздействий, причем учитывая требования качества САР – точность очень важная «характеристика».

Наиболее часто точность САР оценивают по отработке управляющих воздействий. Рассмотрим последовательно различные виды управляющих (задающих) воздействий.

7.2 Точность при постоянном задающем воздействии. Постоянные ошибки

Для упрощения дальнейших преобразований будем считать, что структура САР приведена к стандартному виду (см. п.5 Передаточные функции и уравнения динамики система автоматического регулирования):

Примем, что отсутствует возмущающее воздействие

Рассмотрим единичное ступенчатое воздействие $x(t)=x_0\cdot1(t);$

Считая, что замкнутая САР устойчива, найдем $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Примем, что свободные коэффициенты в полиномах и передаточной функции разомкнутой САР равны 1.

$W(s)=\frac{k\cdot N(s)}{L(s)}$ - передаточная функция замкнутой САР.

Используя передаточную функцию замкнутой САР (см. раздел 5) для ошибки можно записать выражение:

$\Phi_\varepsilon(s)=\frac{E(s)}{X(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.1)}$

где: $\Phi(s)= \frac{k\cdot N(s)}{L(s)+k\cdot N(s)}$ - главная передаточная функция (см. раздел 5).

согласно 1-й предельной теореме (см. раздел 2)

$\lim_{t\rightarrow\infty}\varepsilon(t)= \lim_{s\rightarrow 0}s\cdot E(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.2)}$

Учитывая, что единичное ступенчатое воздействие в отображениях: $x(t)=x_0\cdot1(t)\rightarrow X(s)=\frac{x_0}{s}$ :

$\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot \Phi_\varepsilon(s)\cdot X(s)=\lim_{s\rightarrow 0}\cdot s\cdot\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{x_0}{s}\Rightarrow$ $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\frac{x_0}{k+1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.3)}$

Т.е. если полином имеет свободный член, равный единице, то САР не может точно «отработать» постоянное воздействие, т.е. она статична.

Величина $\varepsilon_{уст}=\frac{x_0}{1+k}$ - называют постоянной или статической ошибкой.

Рисунок 7.2.2 Переходной процесс после ступенчатого воздействия для статичной САР

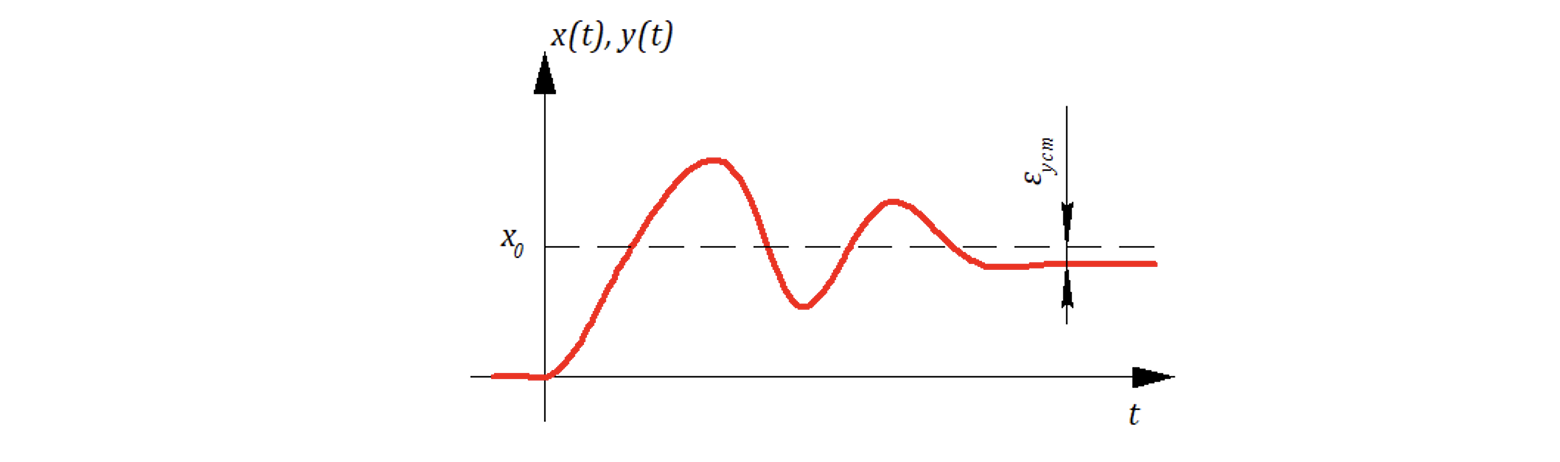
В случае если полином не имеет свободных членов, то его можно представить как $L(s)=s\cdot L_1(s)$ где - полином который имеет свободный член равный единицы. В этом случае установившаяся погрешность:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1+k\cdot N(s)}\cdot\frac{x_0}{s}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.4)}$

Если $L(s)=s^{v} \cdot L_1(s)$ , где - порядок астатизьма, то при постоянном (ступенчатом) воздействии установившаяся ошибка равна нулю.

$\Rightarrow \varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\left\{ \begin{align} &\frac{x_0}{k+1}, если \ \ САР - статическая \\ &0, если \ \ САР - астатическая \end{align} \right.$

Из соотношения 7.2.3 очевидно, чем выше k - коэффициент усиления, тем меньше ошибка (для статических САР). Выводы: необходимо повышать общий коэффициент усиления разомкнутой САР, для сокращения ошибки.

Однако увеличение может привести к резкому уменьшению запасов устойчивости (что ухудшит качество переходного процесса) вплоть до потери устойчивости (см. раздел 6).

Цитата:

"Необходимо отметить, что для разомкнутой САР, имеющей $W(i\cdot\omega)$ годограф похожий на рис. 6.5.5 левый вариант, устойчивость системы (замкнутой) нарушится только с увеличением общего коэффициента усиления К. (Дейстивительно при увеличении коэффициента K увеличится длинна вектора и он может охватить точку -1). "

Поэтому при проектировании САР необходимо «решать» «оптимальную» задачу, т.е. выбрать оптимальное значение , обеспечивающее удовлетворительную точность и неплохое качество переходного процесса.

В последнее время практически все САР проектируются как астатические, что легко достигается за счет использования астатических регуляторов (например ПИ-регуляторов (пропорционально-интегрирующих).

В этом случае говорить о постоянной ошибке нет смысла, т.к. $\varepsilon_{уст}=0$

Пример 1:

Определить установившуюся ошибку, если входное воздействие $x(t)=0.2\cdot1(t)$ , а структура САР имеет вид:

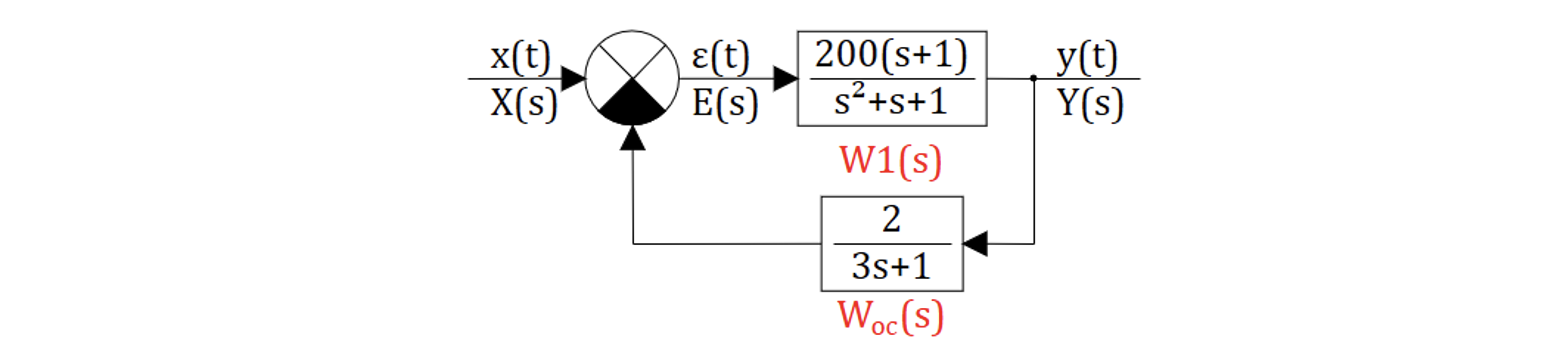
Необходимо заметить, что прямое использование формулы (7.2.3) в данном случае не проходит, т.к. статическая ошибка $\varepsilon_{уст}$ в исходной САР не соответствует статической ошибке в эквивалентной САР:

Прежде чем определять статическую ошибку $\varepsilon_{уст}$ необходимо удостовериться в том, что исходная замкнутая САР устойчива. Выполеним преобразование:

$\Rightarrow \Phi(s)=\frac{W_1(s)}{1+W_1(s)\cdot W_{oc}(s)}=\frac{200\cdot(s+1)\cdot(3\cdot s+1)}{(s+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)}\Rightarrow$

Характерестический полином эквивалентной передаточной функции: $D(s)=3\cdot s^3+4\cdot s^2+404\cdot s+401$

Для определение устойчивости критерий Гурвица (см. раздел 6):

$Г =\left | \begin{matrix}4 \ \ 401 \ \ 0\\ 3 \ \ 404 \ \ 0 \\ 0 \ \ 4 \ \ 401 \end{matrix} \right |=\left\{ \begin{align} &\Delta_1=4>0;\\ &\Delta_2 =\left | \begin{matrix} 4 \ \ 401\\ 3 \ \ 404 \end{matrix} \right |=4\cdot 404-3\cdot401>0; \\ &\Delta_3 =\Delta_2\cdot 401>0; \end{align} \right.$

Все главные определители матрицы Гурвица больше нуля $\Rightarrow$ САР устойчива.

Перейдя к изображению $x(t)=0.2\cdot 1(t)\rightarrow X(s)= \frac{0.2}{s}$ Найдем выражения для отклонение в изображениях:

$E(s)=X(s)-Y_1(s)=X(s)-W_{ос}(s)\cdot Y(s)=X(s)-W_{ос}(s)\cdot W_1(s)\cdot E(s)\Rightarrow$ $E(s)=\frac{X(s)}{1+W_{oc}(s)\cdot W_1(s)}$

Подставляем значения и $W_{oc}$ , имеем:

$E(s)=\frac{0.2}{s\cdot [1+\frac{200(s+1)}{s^2+s+1}\cdot\frac{2}{3\cdot s+1}]}=\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0} s\cdot E(s) = \lim_{s\rightarrow0}s\cdot\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}=\frac{0.2}{401}$ $\varepsilon_{уст}\approx5\cdot10^{-4}$

7.3 Точность при линейном воздействии. Скоростные ошибки

В данном подразделе рассмотрим САР замкнутую единичной обратной связью (если обратная связь не единична, то с помощью структурных преобразований ее можно привести к единичной, подробнее об этом смотри раздел 4 Структурные преобразования систем автоматического регулирования)

Рисунок 7.3.1 САР с единичной обратной связи

где $x(t)=a_0\cdot1(t)+a_1\cdot t$ - входное воздействие.

Рисунок 7.3.2 Линейное входное воздействие

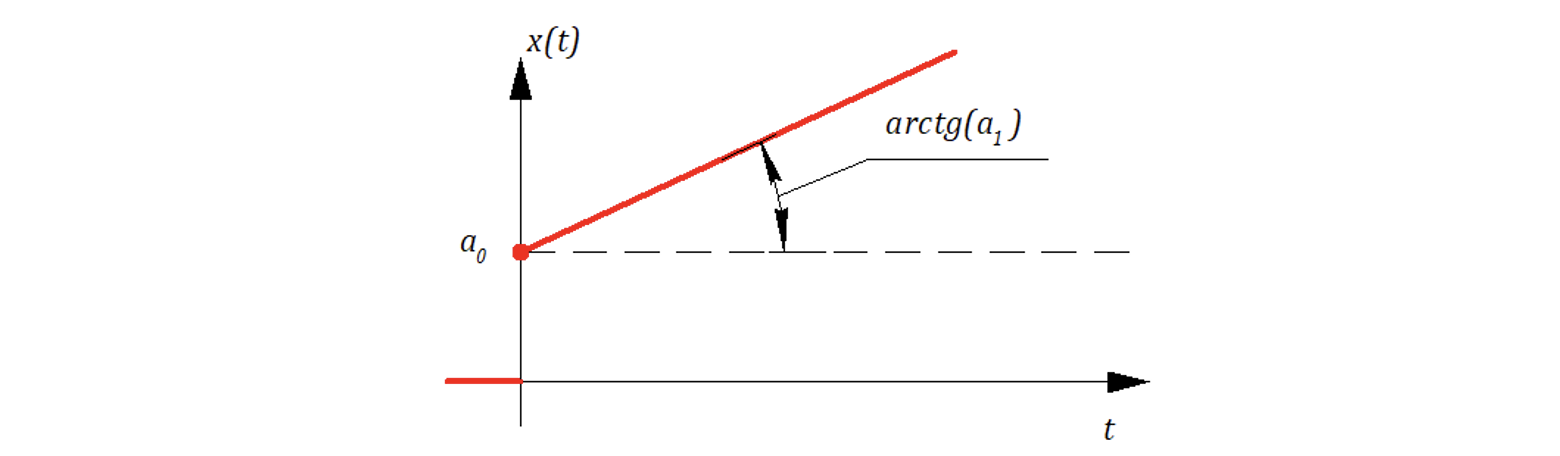
В соответствии со своим назначением устойчивая САР обязана «отслеживать» (с какой-то степенью точности) управляющее воздействие.

Воспользуемся первой предельной теоремой:

$\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot E (s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.1)}$

Рассмотрим различные варианты САР: статическую и астатическую (1-го и 2-го порядка)

Статическая САР

Передаточная функция соответствует статической САР:

$W(s)=\frac{k\cdot N(s)}{L(s)}$

где полниномы и имеют свободный член равный 1.

Отклонение в отображениях:

$E(s)=X(s)\cdot\Phi(s)$

Где - изображение входного воздействия; $\Phi_\varepsilon(s)$ - передаточная функция по возмущению:

$\Phi_\varepsilon(s)=\frac{L(s)}{(L(s)+k\cdot N(s))}$

Изображение входного воздействия $x(t)\rightarrow X(s)$ :

$X(s)=\frac{a_0}{s}+\frac{a_1}{s^2}=\frac{a_0\cdot s+a_1}{s^2}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\Phi_\varepsilon \cdot X(s)=\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\infty$ $\varepsilon_{уст}=\infty \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.2)}$

Вывод: Cтатическая САР не способна «отслеживать» линейное воздействие.

Астатическая САР со степенью астатизма 1

Для САР со степенью астатизма 1 полином не содержит совбодного члена равного 1, но его можно представит в виде произведения $s\cdot L_1(s)$ где - полином содержащий свободный член равный 1.

Примечание: Степень астатизма равна количеству нулевых полюсов полинома (см. раздел 5)

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\frac{a_1}{k}$ $\varepsilon_{уст}=\frac{a_1}{k} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.3)}$

Вывод: Если разомкнутая САР имеет астатизм первого порядка (имеет один нулевой полюс), то установившияся ошибка для замкнутой САР $\varepsilon_{уст}={a_1}/{k}$

Рисунок 7.3.3 Реакция на линейное воздействие САР с астатизьмом 1-го порядка

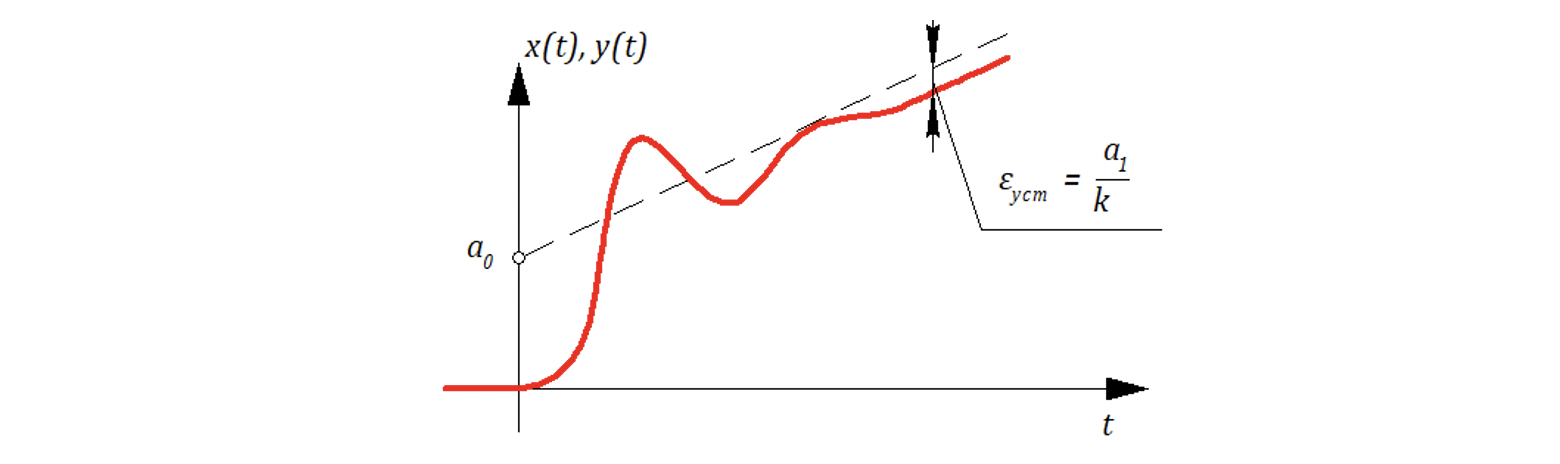
Ошибка в астатической САР (1^-го порядка) называется скоростной ошибкой, а общий коэффициент часто называют коэффициентом добротности или просто добротностью.

Анализ формулы (7.3.3) показывает, что чем выше тем меньше $\varepsilon_{уст}$ . Однако необходимо помнить, что повышение может привести к потери устойчивости САР (или уменьшению запасов устойчивости с соответствующим ухудшением качества переходного процесса).(см. раздел 6).

Астатическая САР со степенью астатизма 2

Для САР со степенью астатизма 2 полином не содержит не только совбодного члена равного 1, и члена у которого степень равна 1. Такой полином можно представит в виде произведения $s^2\cdot L_1(s)$ где - полином содержащий свободный член равный 1.

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s^2\cdot L(s)}{s^2\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=0$ $\varepsilon_{уст}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.6)}$

Рисунок 7.3.4 Реакция на линейное воздействие системы с астатизьмом 2-го порядка

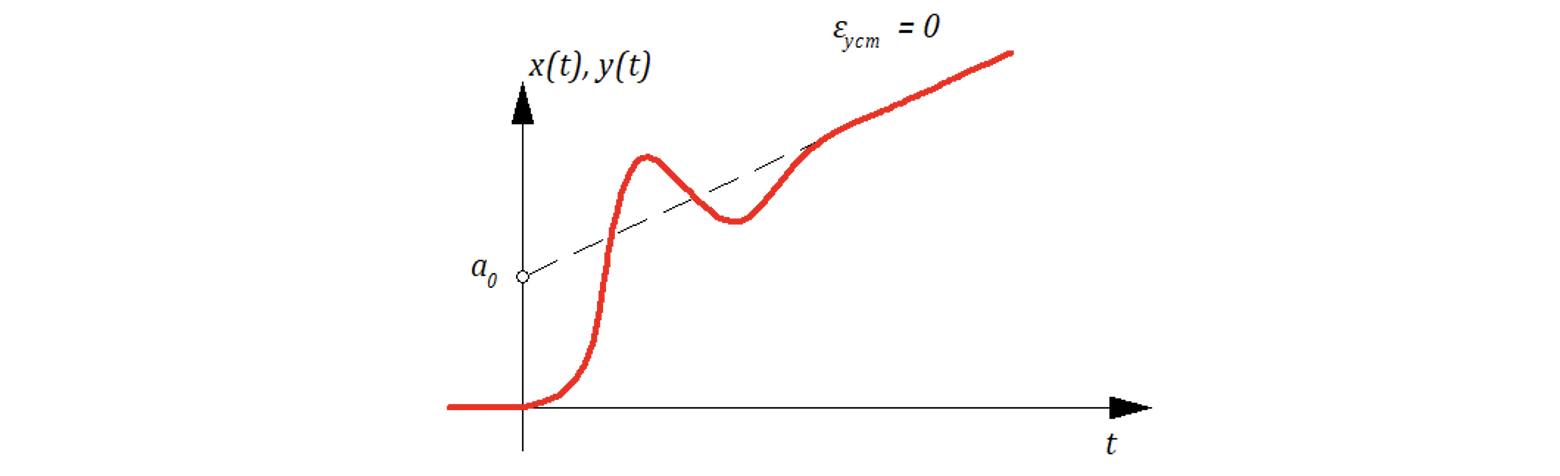
Очевидно, что если степень астатизма >2, то установившаяся статическая ошибка, тем более будет равна 0. Т.е. чем выше астатизм САР, тем лучше точность. Хотя повышение астатизма ухудшает устойчивость (запас устойчивости).

Модели из статьи можно взять здесь...

В предыдущих сериях:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.

Комментарии (5)

p-p-k-55
13.09.2023 05:50
#25958880
+1
Про статические и астатические САР написано. А как насчет изодромных САР?
1. petuhoff Автор
  13.09.2023 05:50
  #25958900
  Прикольно, в стате про изодромное звено потребовали рассказать про астатизм!
  
  Изодром здесь: Изодром
  1. p-p-k-55
    13.09.2023 05:50
    #25960374
    Я правильно понимаю: САР (т.е. система) может быть либо статической либо астатической, а изодромным может быть только звено?
    
    petuhoff Автор
    13.09.2023 05:50
    #25961186
    В теориию любую САР можно заменить одним эквивалентным звеном. https://habr.com/ru/articles/654673/
    
    Arastas
    13.09.2023 05:50
    #25961534
    +1
    Уточню, что в этом случае точность (астатизм) по заданию можно определить по числу совпадающих коэффициентов при младших степенях в числителе и знаменателе, вплоть до первого несовпадения. Так, САР, описываемая изодромом, не обладает астатизмом даже нулевого порядка. :)