О каких законах, принципах и свойствах квантового мира обычно вспоминают люди, думая о физике элементарных частиц?

Кто-то, скорее всего, вспомнит принцип неопределённости Гейзенберга. Он гласит, что существует предел точности, с которой можно одновременно знать некоторые пары физических свойств частиц — например, положение и импульс. Другими словами, чем точнее измеряется одно свойство, тем менее точно может быть известно другое.

Говоря более формально, принцип неопределённости представляет собой одно из множества математических неравенств, накладывающих фундаментальное ограничение на произведение точности некоторых связанных пар измерений квантовой системы, таких как положение, x, и импульс, p. Такие парные переменные называются дополнительными или канонически сопряжёнными переменными. Принцип неопределённости, впервые введённый в 1927 году немецким физиком Вернером Гейзенбергом, утверждает, что чем точнее определено положение частицы, тем менее точно можно предсказать её импульс, исходя из начальных условий, и наоборот.

Кто-то обязательно упомянет двухщелевой эксперимент — важнейший опыт, доказывающий вероятностный характер квантовой механики. В нём видно, как свет и материя одновременно могут вести себя и как волны, и как частицы.

Впервые эксперимент такого типа провёл Томас Юнг ещё в 1801 году для демонстрации волнового поведения видимого света. Он считал, что этот эксперимент демонстрирует правильность волновой теории света Христиана Гюйгенса, и его эксперимент иногда называют экспериментом Юнга или щелями Юнга. А в 1927 году Дэвиссон и Джермер продемонстрировали, что электроны демонстрируют такое же поведение, которое позже было распространено на атомы и молекулы.

В экспериментах такого класса волна разделяется на две отдельные волны, которые затем объединяются в одну волну. Изменение длины пути обеих волн приводит к сдвигу фаз, создавая интерференционную картину. В базовом варианте этого эксперимента когерентный источник света, например лазерный луч, освещает пластину с двумя параллельными щелями, и свет, проходящий через щели, наблюдается на экране за пластиной. Волновая природа света приводит к интерференции световых волн, проходящих через две щели, создавая на экране яркие и тёмные полосы — результат, которого нельзя было бы ожидать, если бы свет состоял из классических частиц.

Однако оказывается, что свет всегда поглощается на экране в отдельных точках, как отдельные частицы (а не как волны); интерференционная картина проявляется в изменении плотности попадания этих частиц на экран. Более того, в вариантах эксперимента, включающих детекторы на щелях, обнаруживается, что каждый обнаруженный фотон проходит через одну щель (как классическая частица), а не через обе (как волна). То есть частицы не образуют интерференционной картины, если фиксировать, через какую щель они проходят.

Другие объекты атомного масштаба, такие как электроны, демонстрируют такое же поведение, если выстрелить ими в сторону двойной щели. Кроме того, обнаружение отдельных дискретных столкновений с экраном носит вероятностный характер, что невозможно объяснить с помощью классической механики. Самыми крупными образованиями, для которых был проведён этот удивительный эксперимент, были молекулы, состоящие из 2000 атомов каждая.

Этот эксперимент, выражающий одну из центральных загадок квантовой механики, Ричард Фейнман назвал «явлением, которое невозможно [...] объяснить никаким классическим способом, и которое содержит в себе сердце квантовой механики. В действительности в нём заключена единственная тайна [квантовой механики]».

Ну и, разумеется, куда же без котиков – про многострадального кота Шрёдингера (в оригинале, кстати, речь шла о кошке) слышали, наверное, даже те люди, которые больше ничего не знают о квантовой механике.

В оригинальной формулировке Шрёдингера в герметичный ящик помещаются кошка, колба с ядом и радиоактивный источник, а также регистрирующий излучение прибор. Если датчик излучения (например, счётчик Гейгера) обнаруживает радиоактивность (т. е. распад одного атома), колба разбивается, выделяя яд, который убивает кошку. Копенгагенская интерпретация квантовой механики (оперирующая волновой функцией квантовой системы) подразумевает, что через некоторое время кошка оказывается одновременно живой и мёртвой. Однако, просто заглянув в коробку, можно увидеть кошку либо живой, либо мёртвой, а не одновременно живой и мёртвой. Это ставит вопрос о том, когда именно заканчивается квантовая суперпозиция и реальность переходит в ту или иную возможность (и это если не углубляться в теорию мультивселенной).

Хотя первоначально этот парадоксальный мысленный эксперимент Шрёдингера был критикой копенгагенской интерпретации, он стал частью фундамента квантовой механики. Этот сценарий часто фигурирует в теоретических дискуссиях об интерпретациях квантовой механики, особенно в ситуациях, связанных с проблемой измерения. В результате мем «кот Шрёдингера» надолго закрепился в популярной культуре. Эксперимент не предназначен для реальных неприятных экспериментов с бедными животными, а скорее является иллюстрацией поведения атомов. Были проведены эксперименты в атомном масштабе, показавшие, что очень маленькие объекты могут существовать в виде суперпозиций; однако наложение на них такого большого объекта, как, например, кошка, создаёт непреодолимые технические трудности.

По сути, эксперимент с кошкой Шрёдингера ставит вопрос о том, как долго существуют квантовые суперпозиции и когда они разрушаются (и разрушаются ли вообще). Были предложены различные интерпретации математики квантовой механики, дающие различные объяснения этому процессу, однако проблема «кошки Шрёдингера» до сих пор остаётся нерешённой.

Однако мало кто вспомнит ещё один фундаментальный закон, управляющий квантовым миром — принцип запрета Паули. А ведь именно благодаря ему такое относительно небольшое количество стабильных атомов (несколько десятков) даёт почти бесконечное многообразие молекул, а также состоящих из них объектов, включая и живых существ. При этом звучит этот принцип весьма просто: в квантовой системе два или более идентичных фермиона не могут одновременно находиться в одном и том же квантовом состоянии. Как это работает?

О том, что вещество состоит из некоторых довольно однообразных мелких частиц, догадывались ещё древние греки. Но прорыв в понимании строения материи произошёл на рубеже XIX и XX веков. В начале XX века в экспериментах Эрнеста Резерфорда было установлено, что атомы состоят из диффузного облака отрицательно заряженных электронов, окружающих небольшое плотное положительно заряженное ядро. Учитывая эти экспериментальные данные, Резерфорд вывел планетарную модель атома — модель Резерфорда 1911 года. В ней электроны вращались вокруг ядра как планеты вокруг Солнца, но при этом возникала техническая трудность: законы классической механики (например, формула Лармора) предсказывают, что электрон, вращаясь вокруг ядра, будет испускать электромагнитное излучение.

Поскольку электрон в этой модели теряет энергию, он быстро закручивается внутрь ядра, в итоге разрушаясь в нем. То есть эта модель предсказывала нестабильность любых атомов, что очевидно противоречило наблюдениям. Кроме того, по мере закручивания электрона внутрь ядра частота излучения должна была быстро возрастать из-за уменьшения периода обращения, что приводило бы к электромагнитному излучению с непрерывным спектром. Однако эксперименты конца XIX века с электрическими разрядами показали, что атомы излучают свет (т. е. электромагнитное излучение) только на определённых дискретных частотах.



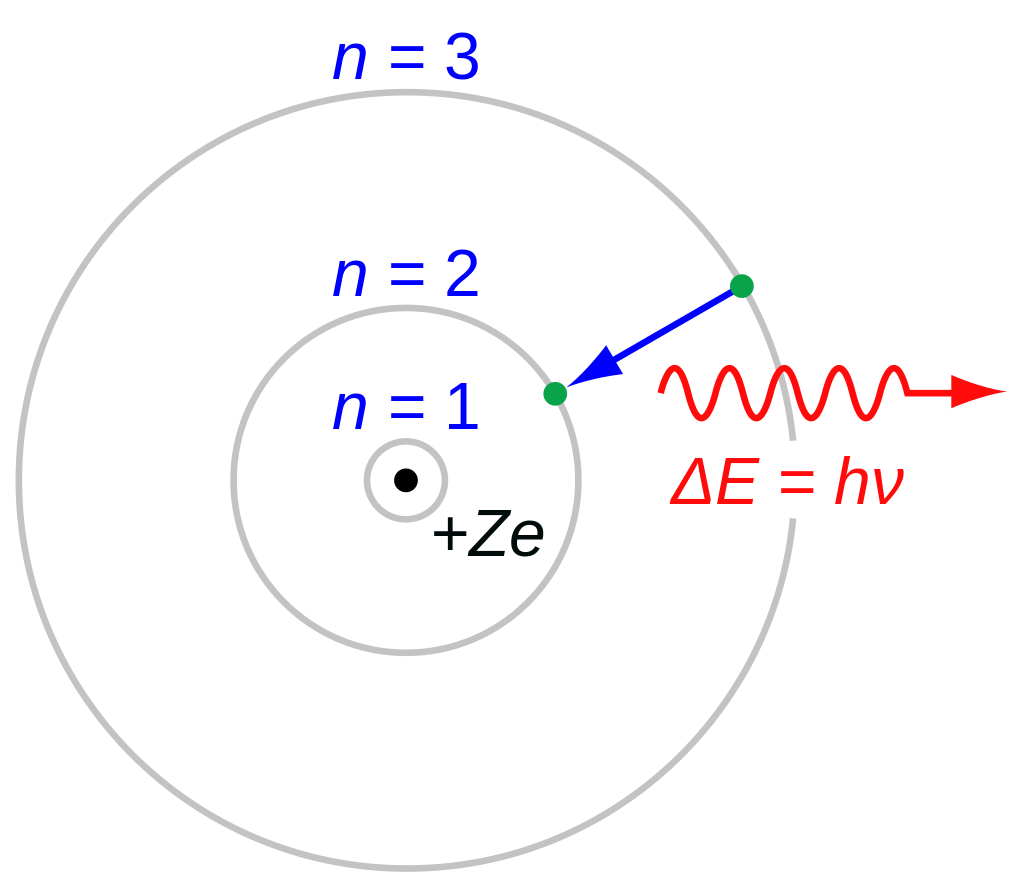
В 1897 году физик лорд Рэлей проанализировал эту проблему. К 1906 году Рэлей заявил, что «частоты, наблюдаемые в спектре, возможно, вовсе не являются частотами возмущений или колебаний в обычном смысле этого слова, а скорее составляют существенную часть первоначальной конституции атома, определяемой условиями стабильности». А к 1913 году свою усовершенствованную модель атома представили Нильс Бор и Эрнест Резерфорд.

Их атом состоит из небольшого плотного ядра, окружённого вращающимися электронами. Его строение аналогично строению Солнечной системы, но притяжение электронов обеспечивается не гравитацией, а электростатическими силами, а энергии электронов квантованы (принимают только дискретные значения). Модель описывала то, что наблюдалось в экспериментах, но не отвечала на вопрос о том, а почему атом устроен именно так и оттуда берутся эти дискретные значения. Тут-то на сцену и вышел Паули.

В ходе экспериментов начала XX века стало очевидно, что атомы и молекулы с чётным числом электронов более устойчивы в химическом отношении, чем с нечётным. Например, в статье Гилберта Н. Льюиса «Атом и молекула», опубликованной в 1916 году, третий из шести постулатов химического поведения гласит, что атом стремится иметь чётное число электронов в любой оболочке, и особенно восемь электронов, которые, по его мнению, обычно расположены симметрично по восьми углам куба. В 1919 году химик Ирвинг Ленгмюр предположил, что периодическую таблицу можно объяснить тем, что электроны в атоме связаны или сгруппированы определённым образом. Считалось, что группы электронов занимают множество электронных оболочек вокруг ядра. В 1922 году Нильс Бор предположил, что определённое число электронов (например, 2, 8 и 18) соответствует стабильным «закрытым оболочкам».

Паули искал объяснение этим числам, которые поначалу были лишь эмпирическими. Одновременно он пытался объяснить экспериментальные результаты эффекта Зеемана в атомной спектроскопии и в ферромагнетизме. Существенный ключ к разгадке он нашёл в работе Эдмунда Стонера, опубликованной в 1924 году, в которой указывалось, что для заданного значения главного квантового числа (n) число энергетических уровней одного электрона в спектрах щелочных металлов во внешнем магнитном поле, где все вырожденные энергетические уровни разделены, равно числу электронов в замкнутой оболочке благородных газов для того же значения n. Это привело Паули к пониманию того, что сложные числа электронов в замкнутых оболочках могут быть сведены к простому правилу: по одному электрону на одно состояние, если определять эти состояния с помощью четырёх квантовых чисел. Для этого он ввёл новое двухзначное квантовое число, которое впоследствии назвали спином электрона.

Именно благодаря этому принципу электроны находятся в атомах на разных орбиталях. На одной орбитали не может находиться неограниченное количество электронов, и поэтому все электроны атома не могут «упасть» до значения с минимальной энергией.

Все электроны Вселенной одинаковы – у всех один и тот же заряд, масса, лептонное число и спин (полуцелый).

Квантовое состояние электрона в атоме определяют его энергетический уровень n, орбитальное квантовое число l (момент импульса и форма орбитали), которое принимает целые значения от 0 до n, и магнитное квантовое число m, принимающее значения от –l до l, а также направление спина.

На самом нижнем энергетическом уровне (n=1, орбиталь 1s) может поместиться один электрон – ему ничего не будет мешать. Туда можно впихнуть и ещё один – однако его квантовые числа согласно принципу запрета Паули должны чем-то отличаться от квантовых чисел первого. Единственное, чем они могут отличаться – это противоположной направленностью спина, поскольку на первом уровне l=0 и m=0. После этого нижний энергетический уровень атома оказывается заполненным – других вариантов электронов там быть не может.

Для добавления третьего электрона необходимо перейти на следующий энергетический уровень (n = 2). Орбиталь 2s (где l = 0) может вместить ещё два электрона, и тогда нужно перейти на орбиталь 2p, где l = 1, и на ней уже могут быть электроны с магнитными квантовыми числами: -1, 0 или +1, на каждое из которых может приходиться по два электрона со спином +½ или -½.



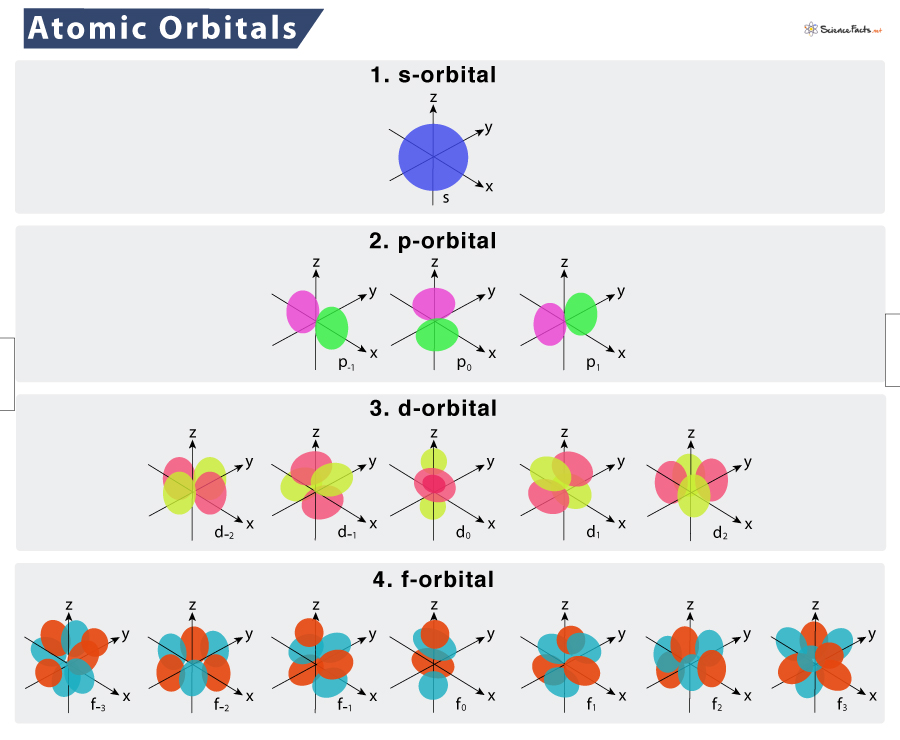
Чем больше электронов нам нужно разместить в атоме, тем больше у него должно быть энергетических уровней и орбиталей различных форм. В результате у разных элементов периодической таблицы будет разная конфигурация электронов на внешних оболочках, и вести они себя при формировании атомных, ионных и молекулярных связей будут по-разному. У каждого нового электрона в атоме должны быть другие квантовые числа, не такие, как у остальных. Это и есть принцип Паули.

Без этого принципа все атомы были бы похожи друг на друга и на атом водорода – простейший из них, и кроме звёзд, чёрных дыр газа и пыли в такой вселенной ничего другого просто не было. Нейтронных звёзд и карликов разных мастей появиться бы не могло – они все под воздействием гравитации сколлапсировали бы в чёрные дыры.

Ещё можно представить себе появление жизни без квантовой неопределённости или корпускулярно-волнового дуализма – но никакие сложные формы жизни, включая нашу, основанную на углероде, так никогда бы и не появились, не будь в природе принципа Паули.

Узнавайте о новых акциях и промокодах первыми из нашего Telegram-канала ????