«Теория тем более впечатляюща, чем проще ее предпосылки» (Альберт Эйнштейн)

«Видеть вещи не такими, каковы они есть, а такими, какими могли бы быть» (Кай Берд, Мартин Дж. Шервин, «Оппенгеймер. Триумф и трагедия Американского Прометея»)

«В науках мы ищем причин не столько того, что было, сколько того, что могло бы быть» (Томас Гоббс)

«Я думаю, что важно относиться к науке не как к предприятию, цель которого – делать предсказания, а как к предприятию, целью которого является открытие того, как на самом деле выглядит мир, что существует на самом деле, как оно ведёт себя и почему» (Дэвид Дойч)

Пока большинство физиков-теоретиков заняты поисками фундаментальной «теории всего», которая должна объединить квантовую теорию поля с общей теорией относительности, некоторые учёные смотрят на это скептическим взглядом и предлагают двигаться совсем в другом направлении. Один из них – Дэвид Дойч – британский физик израильского происхождения, профессор Оксфордского университета, автор книг «Структура реальности» (1997) и «Начало бесконечности» (2011). С 2012 г. он вместе с итальянкой Кьярой Марлетто работает над теорией конструкторов, призванной – ни много ни мало – объединить все наши знания о реальности в единый набор мета-законов, или фундаментальных принципов, определяющих, что может происходить во Вселенной, а что запрещено. Теория конструкторов преподносится авторами как обобщение теории информации на всю остальную физику, а другие разделы физики, включая термодинамику, статистическую механику, теорию квантовых вычислений и даже квантовую механику – как её производные. Изучение конструкторов, по мнению Дойча, даст нам ключ к пониманию, откуда вообще взялись законы физики и почему они работают именно так, а не иначе. Но насколько оправданы его амбициозные заявления? Не является ли теория конструкторов очередной «теорией чего угодно», не дающей никаких предсказаний и неприменимой на практике?

Теория конструкторов как мета-теория

Дэвид Дойч уже давно критикует редукционистов, которые пытаются свести всё на свете к единому своду законов, управляющих взаимодействиями элементарных частиц. Он считает, что из квантовой механики, управляющей поведением атомов, нельзя вывести, например, дарвиновскую теорию эволюции, управляющую поведением организмов и популяций. Это эмерджентные свойства макроскопических систем, возникающие в одних обстоятельствах и не возникающие в других. Правила репликации генов совсем не похожи на законы движения частиц или перегруппировки атомов, они имеют независимое происхождение. Поэтому Дойч выделяет четыре самостоятельные «нити» структуры реальности: квантовую теорию в интерпретации Эверетта, синтетическую теорию эволюции с уточнениями Ричарда Докинза, теорию вычислений Алана Тьюринга и эволюционную эпистемологию Карла Поппера. Однако за ними может стоять другая, ещё более абстрактная и фундаментальная теория. Возможно, это будет теория конструкторов, но Дойч не исключает существования и следующих уровней обобщения. Например, теория конструкторов может стать лишь частным случаем универсальной теории сложности, изучающей ресурсы, необходимые для выполнения тех или иных вычислений.

Цель теории конструкторов – переформулировать физические законы на языке общих принципов – утверждений о том, какие физические преобразования или задачи возможны, а какие невозможны, и почему. По словам Дойча, «теория конструкторов, если точно, не о конструкторах, а о задачах для конструкции чего-либо: о том, что возможно для конструктора сделать и что невозможно. А возможно то, что не запрещено законами физики».

Можно подумать, что это просто какая-то игра слов, ведь законы физики – это и есть ограничения, определяющие, что возможно, а что нет. Однако в традиционной физике преобладают динамические законы, которые предсказывают, как будут меняться физические переменные микроскопических и макроскопических систем, исходя из начальных условий. То есть механика работает только с преобразованиями, которые фактически происходят, не объясняя, почему они происходит. Существует негласное правило, что все фундаментальные физические теории должны быть сформулированы в виде предсказаний того, как объекты будут перемещаться во времени и пространстве при определенных начальных условиях. Но такой подход не работает, если одни и те же начальные условия при одних и тех же законах движения приводят к разным результатам. С помощью траекторий движения частиц невозможно объяснить такие важные понятия, как температура, давление и работа в термодинамике, информация и вычисления в информатике, знание, сознание и свобода воли в психологии. Физики-редукционисты считают их всего лишь удобными приближениями на некоем уровне эмерджентности. Неудивительно, что термодинамика и даже ньютоновская механика до сих пор носят эвристичный характер: когда работают, тогда работают, а почему – никто не знает.

Вот что говорит по этому поводу сам автор теории:

«Доминирующая в современной науке концепция рассматривает всё вокруг как развивающиеся последствия неких неизвестных начальных условий… К примеру, зная законы движения и то, где находилась планета год назад, мы можем предсказать, где она окажется ещё через год. Но если мы зададимся вопросом, а можем ли мы передвинуть целую планету туда-то и туда-то, традиционный подход даст сбой. Еще один пример — проблема свободной воли. Предположим, у меня есть два варианта выбора. Остановившись на первом, я могу лишь догадываться, что произошло бы, выбери я второй. То, что происходит — происходит. И всё… Получается, что мой выбор был предопределён со времён Большого Взрыва? Глубинная проблема в том, что доминирующая концепция объясняет лишь то, что материально; свободная воля не вписывается в нее… В теории конструкторов можно будет сказать, что что-то возможно, не говоря, что это произойдёт».

Утверждения о том, что может или не может произойти и почему, в теории конструкторов называются контрфактуалами. Факты – это события, которые произошли, а контрфактические события могли бы произойти, но не произошли, или не могли бы произойти в принципе. До недавнего времени считалось, что физика, подобно истории, не терпит сослагательного наклонения, и все эти «если бы» для науки не имеют никакого смысла. Но это было справедливо в рамках ньютоновской механики, где всё жёстко детерминировано. А квантовая механика оперирует только вероятностями, поэтому единичные события невозможно предсказать наверняка. Если игнорировать контрфактуалы, это выглядит как нередуцируемая случайность. Но иногда полезно рассмотреть альтернативные, нереализованные варианты событий. Возможно, вы уже догадались, что контфактуалы – это всего лишь другое название параллельных вселенных из многомировой интерпретации квантовой механики. Но понятие контрфактуалов в теории конструкторов намного расширено. Оно включает и те вселенные, которые невозможны с точки зрения известных нам законов физики, но реализуемы путём вариации этих законов и фундаментальных констант.

Например, принцип сохранения энергии говорит о том, что вечный двигатель невозможен. На языке динамических законов можно только сказать, что вечный двигатель не существует: ни одна точка на траектории движения Вселенной во времени не содержит его при данных конкретных начальных условиях. Но то, что вечный двигатель невозможен, означает, что он не может быть построен ни при каких начальных условиях и ни при каких реальных динамических законах. Это утверждение гораздо более сильное и категоричное, чем любое из утверждений, которые можно сделать о том, что происходит на конкретной траектории. В то же время есть категория физически возможных, но не существующих в нашей вселенной объектов, таких как белые дыры, чёрные карлики, сфера Дайсона или сильный ИИ. Возможность построить паровой двигатель, универсальную машину Тьюринга или квантовый компьютер существовала всегда, но она не была физически реализована или где-то закодирована во Вселенной до тех пор, пока не появились соответствующие технологии. До момента изобретения эти технологии были контрфактическими.

С точки зрения модальной логики наука изучает только действительное и необходимое, но игнорирует ещё одну модальность – возможное. Научные теории касаются только того, что должно произойти во Вселенной или что, вероятно, произойдет, с учетом того, что уже произошло. Но иногда смысл не в том, чтобы сказать, какую трансформацию претерпит система при конкретном наборе начальных условий, а в том, чтобы подумать о всех трансформациях, которые она могла бы претерпеть, и определить те, которым она не может подвергнуться. Как пишет Кьяра Марлетто в книге «Наука о том, что можно, а что нельзя»,

«…ограничиваясь утверждениями о начальных условиях и законах движения, физика упускает нечто существенное, касающееся физической реальности. Контрфактические свойства — это не крошечная диковинка в сфере свойств физического мира. Они играют центральную роль в понимании огромного числа ключевых фактов о физической реальности, которые до сих пор считались эмерджентными, а не фундаментальными».

В теории конструкторов любое научное объяснение – это всегда утверждение о том, что видимо, с точки зрения в основном невидимых элементов. Например, объяснить, почему ночное небо тёмное, невозможно без рассмотрения контрфактической модели, основанной на законах ньютоновской физики, согласно которой всё небо должно быть таким же ярким, как солнечный диск, потому что в бесконечной и стационарной Вселенной нет красного смещения, и при взгляде в любую точку неба вы рано или поздно упрётесь в звезду. Только опровергнув эту модель фактами расширения Вселенной, конечности её возраста, красного смещения и конечности скорости света, вы поймёте, почему небо выглядит именно так, с точки зрения того, как могло бы быть иначе. Контрфактуалы необходимы, чтобы объяснить связь между информацией и такими физическими идеями, как энтропия в термодинамике. Иногда эта связь очевидна: например, площадь горизонта событий чёрной дыры является мерой энтропии дыры и содержащейся в ней информации.

Конструкторы и задачи

В теории конструкторов всё выражается в задачах. Задача – это абстрактная характеристика преобразования с точки зрения входных/выходных пар атрибутов. Свойства информации выражаются как отношения между выполнимыми и невыполнимыми задачами. Задача невыполнима, если существует закон физики, запрещающий ее выполнение с произвольно высокой точностью, и выполнима в противном случае. Когда задача выполнима, для неё можно построить конструктор, выполняющий её с произвольной точностью и надёжностью. Конструктор – это объект, который может вызвать выполнение задачи, сохраняя при этом возможность вызывать её снова. Он осуществляет физические преобразования, не меняясь сам, что позволяет ему выполнять одну и ту же задачу многократно. К вечной мудрости Гераклита «всё течёт, всё меняется» теория конструкторов добавляет, что всё меняется под воздействием чего-то другого. Почти всё, что может произойти, вызывается конструкторами. Самопроизвольные события, вызванные не-конструкторами («нулевыми конструкторами») – редкие исключения. Для выполнения определённой задачи не нужен конкретный конструктор, подойдёт любой, в репертуаре которого есть соответствующее преобразование.

Типичный пример конструктора – 3D-принтер, который может напечатать какой-нибудь объект много раз. На кухне есть такие конструкторы, как электрический чайник, микроволновка и посудомоечная машина, выполняющие задачи соответственно кипятить воду, подогревать пищу и мыть посуду. В промышленности конструктор – это компьютерная программа, управляющая автоматизированной фабрикой. В химии примером конструкторов являются катализаторы – молекулы, которые увеличивают скорость химических реакций, но не вступают в эти реакции и не меняются сами. В термодинамике конструктор – это тепловая машина, работающая по циклу Карно. В информатике конструктор – это компьютер, который выполняет всевозможные операции по обработке информации, оставаясь неизменным физически. В биологии конструктором является репликатор, побуждающий среду его копировать. А в человеческой культуре конструкторы – это мемы.

Знание – тоже разновидность конструктора, независимо от того, что является его носителем: мозг, компьютер или книга. «Знания определяются полностью через контрфактуалы: это информация, которая способна оставаться реализованной в физических системах. В отличие от большинства определений знания, это хорошо тем, что оно не зависит от наличия познающего субъекта». От количества знания, которое теоретически можно измерить, зависит возможность новых преобразований окружающей среды. Многие преобразования не могут быть выполнены без определённых теоретических и технических знаний. Поэтому теория конструкторов объясняет, как знания создаются и применяются. Впервые за последние несколько столетий она возвращает человека из задворок Вселенной на центральное место в научной картине мира, как творца знания. Ведь почти все существующие конструкторы созданы искусственно – нами. Мы – тоже в значительной степени конструкторы, хотя сегодня среднестатистический человек может осуществить гораздо меньше физических преобразований, чем охотник-собиратель каменного века. Но мы обрабатываем огромное количество информации и эффективно обмениваемся ею. Поэтому современное человечество в целом способно на большее, чем человечество на любом этапе в прошлом.

Конструкторская теория жизни и универсальный конструктор

Кьяра Марлетто утверждает, что живые существа выделяются из физического мира таким свойством, как устойчивость, т.е. способность поддерживать своё существование в изменяющейся среде. Камень кажется незыблемым и вечным, но он подвержен воздействию воды и ветра, отчего медленно, но необратимо разрушается. Кролик кажется более уязвимым и недолговечным, но в случае ранения он может восстановится, а в случае смерти его потомство продолжит существовать как вид, гораздо дольше, чем камень. Законы физики не гарантируют достижение устойчивости, но и не запрещают, поэтому устойчивость может быть достигнута безо всякого высшего замысла. Однако объяснить появление жизни не получится без указания её контрфактических свойств: способности репликаторов воспроизводить себя, устойчивости и «иллюзии замысла», т.е. того, что может сделать конкретная совокупность атомов при наличии соответствующих входных данных. Самовоспроизведение (репликация) и естественный отбор возможны без «тонкой настройки», при условии, что законы физики позволяют цифровой информации быть физически реализованной.

Машина, которая имеет в своём репертуаре все физически возможные преобразования, называется универсальным конструктором. Универсальный конструктор – это конструктор, который может при наличии необходимой информации подвергнуть любые объекты любым физически возможным трансформациям. Такая машина, впервые концептуализированная Джоном фон Нейманом, имеет в своём репертуаре не только вычисления, но и общие построения, включая термодинамические процессы (например, охлаждение различных систем), биологические процессы (например, саморепликацию) и вообще всё, что разрешено законами физики. В 1949 г. фон Нейман в своей лекции, прочитанной в Университете Иллинойса, отметил, что его цель – создание машины, которая могла бы автоматически самоусложняться, подобно биологическим организмам в условиях естественного отбора. По мнению фон Неймана, порог сложности, который необходимо преодолеть для реализации такой машины – это создание репликатора или самовоспроизводящейся машины, которая при запуске будет копировать сама себя. Самовоспроизводящаяся машина должна состоять из трёх частей: «описания» самой себя («чертежа» или программы), универсального механизма-конструктора (который может прочитать любое описание и построить машину, закодированную в этом описании) и универсального копировального аппарата (способного делать копии любого описания).

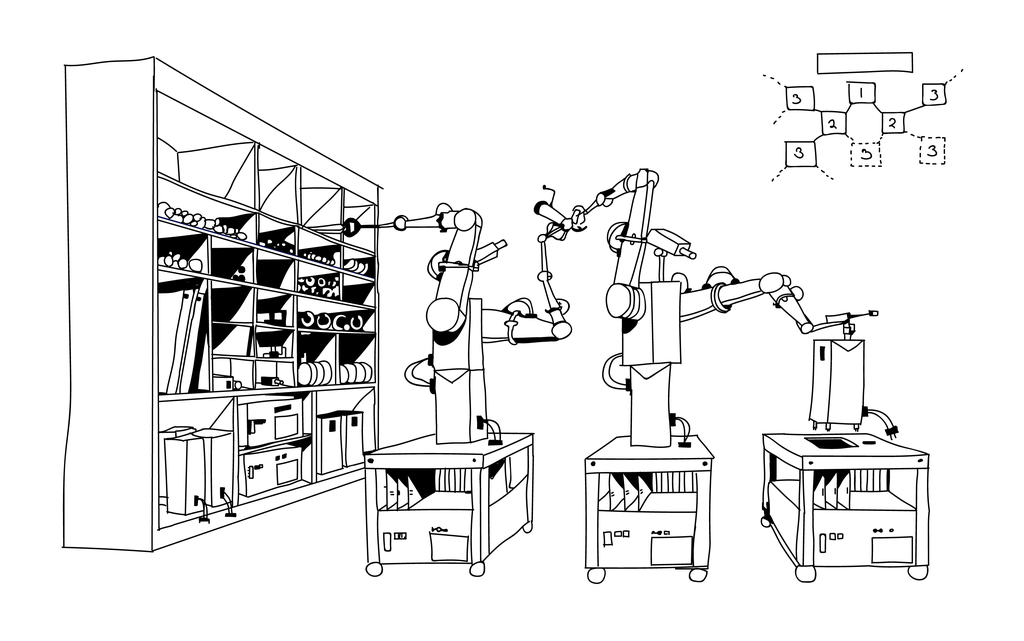
Если универсальная машина Тьюринга – это обобщение классического компьютера, то универсальный конструктор можно рассматривать как обобщение 3D-принтера: при наличии соответствующей программы и достаточного количества сырья он может сконструировать любую систему, существование которой не противоречит законам физики, включая копию самого себя. Человек является универсальным конструктором в том смысле, что потенциально может достичь чего угодно, если это не запрещено законами физики. Но существуют преобразования, которые мы никогда не выполним (по крайней мере, хочется на это надеяться) в силу того, что они аморальны – например, уничтожить планету Земля. Также человек пока не является репликатором – он воспроизводит только половину своих генов, хотя генетические технологии уже позволяют создать клона. Биологическими репликаторами являются гены, но они являются лишь инструкциями по сборке организма, которые могут быть прочитаны только в определённой среде. А универсальный конструктор должен самовоспроизводится в любой среде, где есть достаточно физических ресурсов.

Пока мы можем только гадать, как будет выглядеть универсальный конструктор и обретёт ли он сознание. Можно предположить, что он объединит в себе свойства биологического репликатора, универсального компьютера, нейросети, нанобота и 3D-принтера. Будет ли он изобретён человеком, появится в ходе эволюции искусственного интеллекта или станет результатом интеграции биологического и электронного разума? Может ли универсальный конструктор заменить или поглотить все формы жизни и разума, существующие на данный момент? На эти вопросы у нас пока нет ответов, но ясно одно: обладая практически безграничными возможностями, универсальный конструктор легко захватит достижимую часть наблюдаемой Вселенной и преобразует её до неузнаваемости. Более того, если законы физики не запрещают создание новых вселенных, универсальный конструктор справится и с этой задачей. Тогда автоматически решается проблема «тонкой настройки» физических констант: Вселенная «тонко настроена» не на зарождение жизни или человеческого разума, а на создание универсального конструктора. Законы природы должны быть такими, чтобы мог появится универсальный конструктор, а человек – всего лишь промежуточный этап универсальной эволюции.

Конструкторская теория классической информации

Теория конструкторов объясняет смысл такого простого и в то же время загадочного понятия, как информация. Раньше считалось, что информация не имеет ничего общего с физикой. Мы называем информацией содержание книг, газет, журналов, электронных писем и сообщений, наших разговоров, невербальных сигналов, мелодий и поэзии, цепочки генов в молекуле ДНК и многое другое. Информация больше похожа на абстрактную сущность, которая может принимать самые разные физические формы. Она переносится при помощи электромагнитных, звуковых, нейтринных или гравитационных сигналов, частоту, длину волны и энергию которых мы распознаём как цвет, звук, искривление пространства-времени и т.д. Но частота и энергия – это фактические свойства, они определяются исключительно состоянием системы в определённое время и в определённом месте. А информация – это набор контрфактических свойств. Её количество не получится вычислить, просто описав полное состояние системы со всеми её параметрами. Количество информации связано с возможностью или невозможностью определённых преобразований.

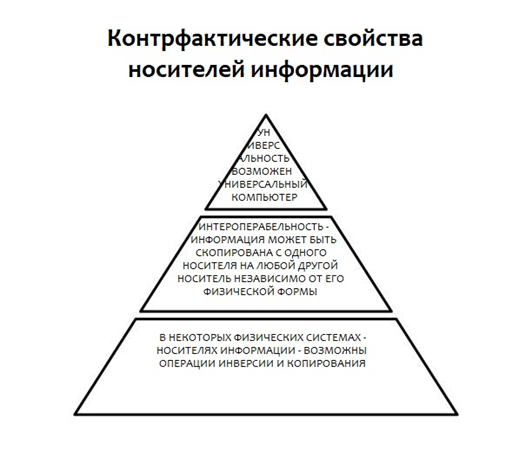
Как пишет Кьяра Марлетто в книге «Наука о том, что можно, а что нельзя», физическая система способна нести информацию, если она обладает двумя контрфактическими свойствами: а) она может быть установлена как минимум в два состояния (операция инверсии возможна в соответствии с законами физики) и б) каждое из этих состояний можно скопировать (операция копирования возможна по законам физики). Первое из этих свойств необходимо для передачи самого элементарного сигнала – двоичного. Состояния системы обозначаются любыми двумя символами: 0 и 1, ON и OFF и т.д. Главное, чтобы их можно было преобразовать одно в другое:
1 → 0
0 → 1
Действительно, объект является носителем информации только в том случае, если его состояние могло бы быть иным: память компьютера бесполезна, если все изменения ее содержимого с течением времени предопределены на заводе.

Второе свойство необходимо для того, чтобы состояния системы могли быть получены и распознаны в каком-либо другом месте. Это преобразование, которое точно передаёт значение, имеющееся в одной системе, в другую систему, сохраняя при этом значение первой:
10 → 11
00 → 00
Здесь важно отметить, что для операции копирования достаточно, чтобы обе системы были носителями информации. Совершенно не обязательно присутствие сознательного наблюдателя, который интерпретирует информацию в процессе измерения, как предполагают квантовые мистики.

«Контрфактический подход также освобождает информацию от субъективности. Когда мы говорим, что некоторый набор состояний может быть скопирован, нам не нужно ссылаться на какой-либо сознательный субъект или наблюдателя, выполняющего это преобразование. Простая химическая реакция, в которой структура некоторого кристалла воспроизводится снова и снова, реализует операцию копирования, и она может делать это в отсутствие направляющей сущности».

По мнению Кьяры Марлетто, указанные трансформации лежат в основе всех вычислений и устанавливают связь между теорией информации и физикой:

«Вот причина, по которой информация является физическим свойством: несёт ли какая-либо система информацию, зависит от того, допускают ли законы физики эти два преобразования в этой системе. Если их нет, то система не может нести информацию. Во вселенной, где ни одна система не обладала бы обоими свойствами, информации не существовало бы. Таким образом, разрешена ли информация или нет, зависит от того, допускают ли законы физики определенные виды контрфактуалов. Но это не свойство, подобное определенному цвету или массе, — фактическим свойствам системы. Это контрфактическое свойство, потому что то, содержит ли система информацию или нет, зависит от того, могут ли быть реализованы в ней эти два преобразования. С помощью контрфактуалов мы пришли к неуловимой связи между информацией и физикой!».

Специалисты по информатике наверняка узнали в упомянутых преобразованиях элементарные логические операции, из которых состоит работа любого компьютера. Компьютер обрабатывает цифровую информацию с помощью логических элементов (вентилей или гейтов) – физических устройств (как правило, транзисторов), выполняющих логическую операцию над входными сигналами (операндами). В зависимости от количества бит на входе операции бывают унарными, бинарными, тернарными и т.д. Унарных операций всего четыре, их выделяют два типа:

1) Операция «НЕ» (NOT) – отрицание (инверсия). На выходе будет «1» тогда и только тогда, когда на входе «0», а «0» тогда и только тогда, когда на входе «1».

2) Операция «копировать» – повторение. Выходная логическая переменная равна входной.

Обратите внимание, что операция «НЕ» важнее, чем повторение, поскольку двойное её применение будет равнозначно копированию исходного бита. Повторитель (буфер) можно собрать из двух инверторов, а инвертор из двух повторителей – нельзя.

Путём комбинирования унарных операций можно составить 16 бинарных операций с двумя битами на входе и одним на выходе. Вот 6 наиболее распространённых из них:

1) Операция «И» (AND) – конъюкция (логическое умножение). На выходе будет «1» тогда и только тогда, когда на всех входах действуют «1», а «0» тогда и только тогда, когда хотя бы на одном входе действует «0».

2) Операция «ИЛИ» (OR) – дизъюкция (логическое сложение). На выходе будет «1» тогда и только тогда, когда хотя бы на одном входе действует «1», а «0» тогда и только тогда, когда на всех входах действуют «0».

3) Операция «И-НЕ» (NAND) – инверсия конъюкции (штрих Шеффера). На выходе будет «1» тогда и только тогда, когда хотя бы на одном входе действует «0», а «0» тогда и только тогда, когда на всех входах действуют «1».

4) Операция «ИЛИ-НЕ» (NOR) – инверсия дизъюкции (стрелка Пирса). На выходе будет «1» тогда и только тогда, когда на всех входах действуют «0», а «0» тогда и только тогда, когда хотя бы на одном входе действует «1».

5) Операция «исключающее ИЛИ-НЕ» (XNOR) – эквивалентность (равнозначность, тождество). На выходе будет «1» тогда и только тогда, когда на входе действует чётное количество «1» или «0», а «0» тогда и только тогда, когда на входе действует нечётное количество «1».

6) Операция «исключающее ИЛИ» (XOR) – сложение по модулю 2 (неравнозначность, инверсия равнозначности). На выходе будет «1» тогда и только тогда, когда на входе действует нечётное количество «1», а «0» тогда и только тогда, когда на входе действует чётное количество «1».

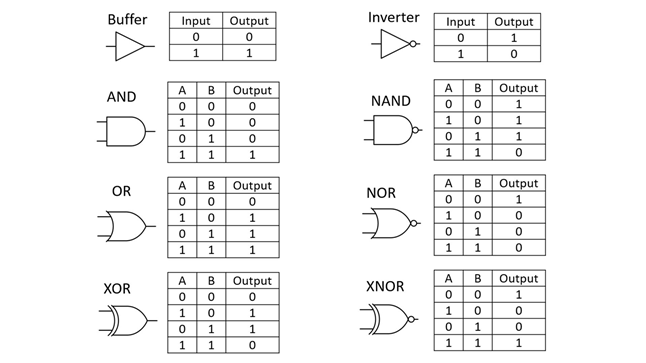
С помощью этих логических операций, реализованных на миллиардах транзисторов современного компьютера, можно составить любой алгоритм и выполнить любое вычисление с любым количеством битов. Теоретически универсальный компьютер способен выполнить все вычисления, разрешённые законами физики: достаточно загрузить в него нужную программу, и он смоделирует любую другую физическую систему. Здесь, как вы уже заметили, всё основано на контрфактических свойствах: какие вычисления может или не может выполнять компьютер, зависит от того, что разрешают законы физики. Об этом говорили Рольф Ландауэр, Пол Бениофф и Ричард Фейнман, но идея была впервые полностью выражена Дэвидом Дойчем и развита учёным-компьютерщиком Чарльзом Беннеттом.

Теория конструкторов заставляет переосмыслить отношения между абстрактными и естественными науками. Традиционно математические абстракции считались чем-то вроде трансцендентных сущностей или платоновских идей, несовершенными проявлениями которых являются физические объекты. Поскольку «книга природы написана на языке математики», этот язык рассматривался как более фундаментальный, чем язык физики. Но теория конструкторов переворачивает устоявшуюся иерархию наук и указывает, что основания математики следует искать в информатике, а законы информации и вычислений – ни что иное, как законы физики. Вычисления – это физические процессы, идущие в вычислителях, которые нужны для моделирования в виртуальной реальности абстрактных сущностей (чисел, уравнений). Математические доказательства – тоже вычисления, которые осуществляются в физическом мире мозгом, классическим или квантовым компьютером. Теория доказательств определяет, что является корректным вычислением или доказательством, а что не является, исключая тем самым ложные объяснения и при помощи эксперимента выявляя математические истины, которые имеют смысл в нашем физическом мире. Получается, что не физика определяется математикой, а наоборот: наши математические знания определяются физикой, ведь математик, как и любой компьютер – это физический объект, который может описать поведение математических объектов.

Классический бит в обобщении теории конструкторов рассматривается как носитель информации – система с набором атрибутов, которые можно переставлять и копировать. Если в системе есть набор атрибутов, набор перестановок этих атрибутов рассматривается как набор задач. Вычислительная среда – это система, атрибуты которой меняются так, чтобы всегда производить выполнимую задачу. Набор перестановок и, следовательно, задач – это набор вычислений. Если возможно скопировать атрибуты в наборе вычислений, носитель вычислений также является носителем информации. Способность информации быть записанной в разных физических системах или на разных носителях называется функциональной совместимостью, а возможность её копировать с одного носителя на другой, сохраняя при этом все контрфактические свойства – интероперабельностью. Объединив две системы, определяемые как биты, будь то фотоны, спины электронов или бинарные переключатели, вы получите ещё один носитель информации с теми же контрфактическими свойствами, что и у его составляющих.

Конструкторская теория квантовой информации

Главным успехом своей теории конструкторов Дэвид Дойч считает объединение классической и квантовой теории информации. Ранее принципы классической теории информации Шеннона были неприменимы к квантовым компьютерам, и алгоритмы для их работы разрабатывались методом проб и ошибок. В 1985 г. Дэвид Дойч доказал, что квантовый компьютер является универсальным компьютером, и сформулировал расширенный вариант тезиса Чёрча-Тьюринга, сегодня известный как тезис Чёрча-Тьюринга-Дойча или CTD-принцип, согласно которому универсальный компьютер способен моделировать любой конечный физически возможный процесс. Чтобы понять, о чём речь, нужно вспомнить, что такое классический универсальный компьютер, описанный Аланом Тьюрингом. Простейший вариант такого компьютера – машина Тьюринга – может выполнить любые вычисления, которые математик проделал бы на бумаге, без учёта ограничений по времени работы и объёму памяти. Так вот, Дэвид Дойч выяснил, что квантовый компьютер теоретически способен выполнить все те же вычисления, что и универсальная машина Тьюринга.

Конечно, на практике до этого ещё далеко, поскольку даже современные технологии не позволяют удерживать достаточное количество кубитов в чистом квантовом состоянии, необходимом для квантовых вычислений. Но звучит вроде бы логично: любая вычислительная задача, решаемая классическим компьютером, может быть решена квантовым компьютером, и наоборот. Причём работу обоих компьютеров можно смоделировать с помощью простейшей машины Тьюринга или даже вручную с помощью ручки и листа бумаги, если у вас хватит на это времени. То есть квантовые компьютеры не дают дополнительных возможностей по сравнению с классическими с точки зрения вычислимости. Например, они не могут решить проблему остановки, неразрешимую для классического компьютера. Так зачем тогда нужны квантовые компьютеры?

Дело в том, что универсальная машина Тьюринга, репертуар которой содержит репертуары всех других машин Тьюринга, не является универсальным компьютером в строгом смысле слова. Есть задачи, которые не подпадают под репертуар вычислительных задач – например, самовоспроизведение или моделирование некоторых физических процессов. Машина Тьюринга способна выполнять только классические вычисления, она не учитывает возможность квантовой интерференции между состояниями бумажной ленты в параллельных вселенных. Кроме того, машина Тьюринга оперирует только с вычислимыми объектами, а в классической физике используются невычислимые понятия непрерывности и континуума. Дэвид Дойч предположил, что квантовый компьютер сможет преодолеть это ограничение, поскольку теоретической основой любых физических процессов, включая работу классических компьютеров, являются законы квантовой физики, в которой есть только дискретные и вычислимые величины.

Дойч выдвинул в качестве кандидата на роль универсального компьютера квантовую машину Тьюринга – абстрактную машину, моделирующую квантовые алгоритмы. В её репертуаре есть операции, которые ни один математик никогда, даже в принципе, не сможет выполнить. Сейчас возможность сверхтьюринговых вычислений активно изучается цифровой физикой. Будучи пионером в этой области, Дэвид Дойч утверждает, что квантовое вычисление – это качественно новый способ использования природы. Квантовые компьютеры могут эффективно передать любую физически возможную квантовую среду, используя для вычисления интерференцию огромного множества параллельных вселенных. Это позволяет ему эффективно решать определённые математические задачи (например, разложение на множители), которые с классических позиций являются труднообрабатываемыми, а также осуществлять классически невозможные разновидности криптографии. Таким образом, законы физики делают универсальное вычисление, при помощи которого можно передать любую физически возможную среду, не просто возможным, но и легкообрабатываемым. Можно ли построить универсальный квантовый компьютер в реальности, зависит только от законов физики и доступных ресурсов.

Квантовая теория информации рассматривается в теории конструкторов как частный случай классической теории информации. Соответственно частным случаем носителя информации является суперинформационный носитель, обладающий всеми свойствами квантового носителя информации, но не обязательно подчиняющийся всем принципам квантовой теории. Среды, способные выполнять квантовые вычисления, называются суперинформационными средами. Квантовый носитель информации, или кубит, имеет два контрфактических свойства: а) невозможность копирования некоторых информационных переменных и б) обратимость всех преобразований, связанных с этими переменными. В них легко узнать принцип неопределённости Гейзенберга и принцип унитарности операторов.

В квантовой теории информации измерение (или «наблюдение») – то же самое, что и копирование, поскольку чистое состояние измеряемого объекта разрушается, а информация о нём передаётся измерительному прибору. Фундаментальное различие между классическими и квантовыми системами Дойч и Марлетто видят в невыполнимости задачи копирования чистого квантового состояния, известной учёным с 80-х гг. как теорема запрета клонирования для квантовых систем. Частным случаем этого закона является принцип неопределённости Гейзенберга: в квантовой системе есть несовместимые переменные (например, координата и импульс), которые нельзя измерить одновременно со сколь угодно высокой точностью. Согласно теории конструкторов, система является неклассической (квантовой), если имеет хотя бы две переменные, которые не могут быть скопированы одновременно одним и тем же конструктором. А классическая механика, наоборот, работает со средой, в которой можно точно копировать состояния. В идеале система задач, выполнимых для этой среды, должна соответствовать шенноновской теории информации.

Принципы обратимости и некопируемости определяют различия между классическими и квантовыми гейтами (логическими элементами). В частности, в квантовой вычислительной среде не работает операция копирования, а также необратимые логические операции AND, OR и производные от них, поскольку число кубитов на выходе должно быть равно числу кубитов на входе. С другой стороны, операция NOT (инверсия) осуществляется тремя разными гейтами, поскольку инвертировать кубит можно по трём разным осям (X, Y или Z). Среди двухкубитных гейтов наиболее распространены CNOT (контролируемое отрицание), HAD (вентиль Адамара, перевод в суперпозицию) и SWAP (обмен вероятностями между двумя кубитами), а среди трёхкубитных – CSWAP (вентиль Фредкина, контролируемый обмен вероятностями) и CCNOT (вентиль Тоффоли, обращает значение последнего бита только если два первых входа равны единице, в противном случае все входы подаются на выход неизменными).

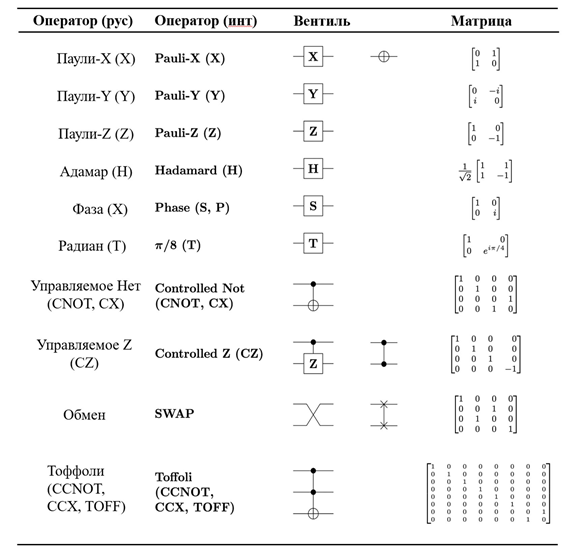
Преимущество теории конструкторов состоит в том, что она выражает характеристики информационных сред независимо от деталей, не привязываясь к законам движения квантовой или классической механики. Копируемость одних свойств, невозможность копирования других и обратимость – это общие принципы, связывающие элементарные частицы и макроскопические объекты. Это значит, что квантовые и классические среды прекрасно совместимы друг с другом, несмотря на существование у первых двух дополнительных свойств: обратимости и некопируемости определённых наборов состояний. Даже если квантовая физика будет заменена более совершенной теорией, аппарат теории конструкторов останется применим и к ней, потому что у него более глубокие основания.

Конструкторская теория термодинамики

Термодинамические понятия работы и теплоты, которые являются ключом к пониманию необратимости, диссипации энергии и стрелы времени, также относятся к контрфактическим свойствам. Как известно, все законы квантовой механики симметричны во времени, из них никак не получается вывести второй закон термодинамики. Квантовая механика не может объяснить, почему некоторые преобразования между состояниями возможны, а некоторые нет. Речь идёт о необратимых на практике процессах типа растворения краски в воде, рассеяния энергии и т.д., которые на квантовом уровне вполне обратимы. Теория конструкторов даёт этому объяснение, основанное на самих преобразованиях, а не на их компонентах. Например, закон сохранения энергии означает, что задача «создание энергии» для любого конструктора ограничивается невозможностью делать энергию из ничего. Но теория конструкторов идёт дальше и объясняет, как приметить законы термодинамики к неизолированным системам.

Необратимость в теории конструкторов означает, что определённая задача выполнима, а её транспонирование (инвертирование) – нет. Например, можно построить конструктор, который будет увеличивать температуру воды, но невозможно сделать так, чтобы он ещё и охлаждал воду. Или можно сделать 3D-принтер, который напечатает дом, но он не сможет этот дом разобрать на исходные стройматериалы. Иногда конструктор хорошо выполняет прямую задачу, но не так хорошо – обратную. По мнению Кьяры Марлетто, причина необратимости заключается в том, что большинство сложных задач выполняются конструкторами, приспособленными к определённой среде. Для выполнения задачи конструктору всегда необходима информация из среды, но обратная задача будет начинаться с другой среды, поэтому тот же конструктор необязательно сработает. «Мы показали, что существуют некоторые преобразования, для которых можно найти конструктор для одного направления, но не для другого» – говорит Марлетто.

В 2022 г. Кьяра Марлетто и Влатко Ведрал из Оксфорда вместе со своими итальянскими коллегами подтвердили это предсказание экспериментально на квантовом компьютере. Они рассмотрели преобразование, связанное с состояниями кубитов, которые, как известно, могут существовать в одном из двух состояний или в комбинации (суперпозиции) обоих состояний. Эксперимент показал, что, если число кубитов не очень велико, и вы используете один и тот же ряд многократно, массив становится все менее и менее способным произвести преобразование B1 в B2, и ещё менее способным к обратному преобразованию B2 в B1. Такие системы можно перевести из смешанного состояния обратно в чистое, но при повторном обращении сделать это всё труднее. Получается, что смешанные состояния более устойчивы, чем чистые. Квантовая механика объяснить это не может, но, если заменить правила Борна информационными принципами теории конструкторов, всё становится на свои места. Следовательно, динамика и время производны от вневременных принципов. Второй закон термодинамики имеет не статистическую природу, а выводится из фундаментальных законов квантовой механики и принципов, определяющих, что может произойти, а что нет.

«Чистое состояние – это состояние, для которого мы знаем всё, что можно знать о нем. Но, когда два объекта запутаны, вы не можете полностью определить один из них, не зная о другом. Дело в том, что из чистого квантового состояния легче перейти в смешанное, чем наоборот – потому что информация в чистом состоянии рассеивается запутанностью и ее трудно восстановить. Это можно сравнить с попыткой повторно сформировать каплю чернил после того, как она рассеялась в воде – процесс, в котором необратимость навязана вторым законом». Но в данном случае необратимость является «следствием того, как динамически развивается система. Здесь нет никакого статистического аспекта. Необратимость – это не просто наиболее вероятный, а неизбежный исход, который определяется квантовыми взаимодействиями компонентов». (Кьяра Марлетто)

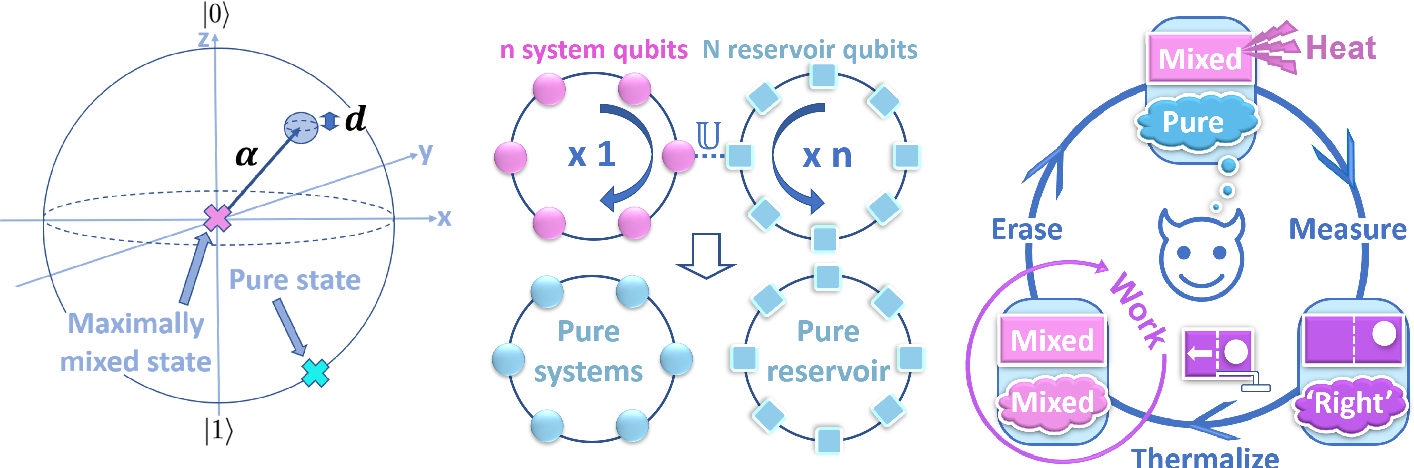
По мнению Кьяры Марлетто, ключ к объединению теории информации и термодинамики – принцип Ландауэра, согласно которому стирание одного бита информации производит энтропию и является логически необратимой задачей. Сейчас команда физиков из Оксфорда пытается доказать, что принцип Ландауэра распространяется и на квантовые компьютеры. Для этого они используют квантовый гомогенизатор – конструктор, который способен приблизительно реализовать преобразование кубита из любого состояния в любое другое состояние и оставаться примерно неизменным посредством в целом полностью унитарных взаимодействий. На практике это просто часть регистра кубитов квантового компьютера. Согласно принципу Ландауэра, перевод кубита в состояние 0 (стирание информации) должен производить энтропию. Действительно, энтропия фон Неймана (неопределённость относительно состояния кубита) нулевая у чистого состояния и максимальна у смешанного. Когда гомогенизатор преобразует смешанное состояние в чистое, энтропия фон Неймана уменьшается за счёт увеличения энтропии кубитов самого гомогенизатора. Фактически гомогенизатор играет роль демона Максвелла, который должен оставлять записи в своей памяти, чтобы отделить «горячие» молекулы от «холодных».

Конструкторская теория квантовой гравитации

Дойч и Марлетто надеются, что теория конструкторов поможет создать набор законов, объединяющий квантовую теорию поля и ОТО, т.е. квантовую теорию гравитации. В этом плане у них уже есть кое-какие идеи. Так, выведенный учёными принцип интероперабельности гласит, что комбинация двух носителей информации тоже является информационным носителем. Наличие в квантовой механике некоммутирующих операторов (координата и импульс, или энергия и время) позволяет реализовать запутанное состояние для составных систем. Если две квантовые системы можно запутать посредством третьей системы, то последняя является как минимум неклассической, то есть обладает квантовой когерентностью. Тогда, если гравитация может запутать две массы, она тоже должна быть неклассической, то есть иметь два несовместимых параметра. Нужно только провести эксперимент, в котором обнаружится запутанность между двумя квантовыми частицами, обусловленная гравитацией. Для этого необходимо ввести в суперпозицию объект массой порядка 10^-12 кг – примерно как человеческая клетка. Если таким образом гравитационная запутанность между массами будет подтверждена, теория конструкторов пройдёт экспериментальную проверку.

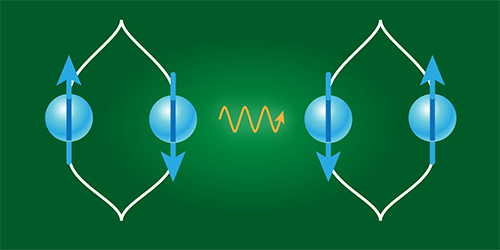
Дэвид Дойч говорит, что разрабатывает теорию «мира, в котором вероятность и случайность полностью отсутствуют в физических процессах». Но это не очередная попытка возрождения классического детерминизма с его «скрытыми параметрами», и не математическая теория наподобие рекурсивно-самовычисляющей Вселенной Стивена Вольфрама, которую Дойч называет «поиском компьютера в небе». Согласно теории конструкторов, не вычисления определяют физический мир, а законы физики определяют вычислимость или невычислимость каких-то функций, решаемость или нерешаемость каких-то задач. Обобщая и улучшая т.н. «подход теории принятия решений», Кьяра Марлетто в своих работах «выводит из физичности» как теорию информации, так и теорию вероятностей, утверждая, что вероятность не имеет физического смысла, она нужна только людям как понятие, на основе которого можно принять какое-то решение и действовать. Да, в квантовой физике несколько последовательных измерений кубита дают разные результаты, но эти результаты не случайны, как не случайны и «разветвления» миров в ММИ. Впрочем, с точки зрения наблюдателя такой подход вряд ли что-то меняет.

Итак, давайте подведём итог. Что же такого нового привносит теория конструкторов в науку, чего нет в других теориях, и в чём заключается её практическая польза? Во-первых, она существенно расширяет предмет изучения физики, включая в него не только факты, но и контрфактуалы. Это переворачивает наши представления о реальности и делает многомировую интерпретацию квантовой механики не столь экзотической, как может показаться на первый взгляд. Во-вторых, она определяет не только то, какие процессы, вероятно, могут произойти, а какие нет, но и то, какие из них в принципе возможны, а какие категорически запрещены. Это необходимо для лучшего понимания эмерджентных явлений, таких как термодинамическая необратимость, эволюция или сознание. В-третьих, она устанавливает тесную связь между физическими объектами и абстрактными вычислениями, причём рассматривает теорию информации и законы физики как фундаментальные ограничения на познание, учитывая физическую природу всех носителей знания и вычислителей. И в-четвёртых, она предсказывает возможность создания универсального конструктора, способного выполнить любое преобразование, не запрещённое законами физики. Дэвид Дойч не сомневается, что однажды мы построим такую машину, и в будущем она станет самым распространённым объектом во Вселенной.