Здравствуйте, дорогие хабровчане, недавно столкнулся с проблемой, связанной с написанием алгоритма из названия в turboprolog2.0, более того я не нашел нигде готовой реализации в трехмерном пространстве на нормальных языках программирования.

Имеется решение только для двухмерного пространства. В связи с чем пришлось придумывать его самому.

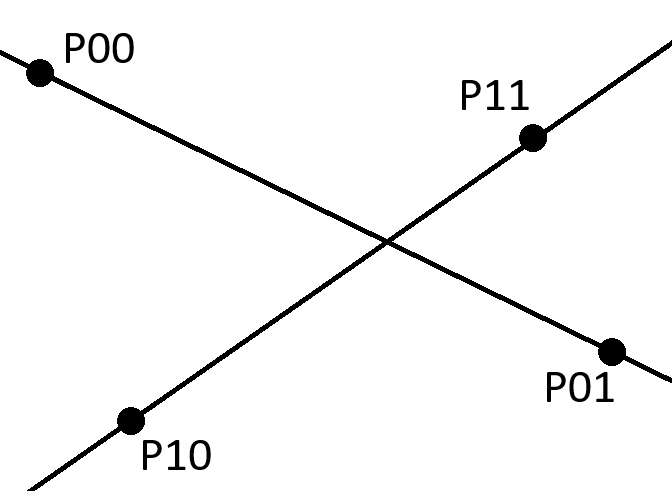
Первая прямая задана точками P00 и P01,а вторая - Р10 и Р11. Каждая точка задана координатами X,Y,Z (например, P00 - X00,Y00,Z00). Требуется найти точку пересечения, если таковая имеется. И проверить принадлежит ли она первому отрезку или находится на его продолжении (первой прямой).

Введем вектора DP0 и DP1, которые параллельны соответствующим им прямым. Вычислим их компоненты.

# вектор первой прямой
DX0 = X01 - X00
DY0 = Y01 - Y00
DZ0 = Z01 - Z00
# вектор второй прямой
DX1 = X11 - X10
DY1 = Y11 - Y10
DZ1 = Z11 - Z10

Точка пересечения прямых принадлежит обеим прямым (очевидно????), и её можно задать формулой.

P = P00 + DP0 * t = P10 + DP1 * s

Разложим в систему:

X00 + DX0 * t = X10 + DX1 * s

Y00 + DY0 * t = Y10 + DY1 * s

Z00 + DZ0 * t = Z10 + DZ1 * s

Удобнее представить систему в таком виде:

DX0 * t - DX1 * s = X10 - X00

DY0 * t - DY1 * s = Y10 - Y00

DZ0 * t - DZ1 * s = Z10 - Z00

Если система имеет решение, то через s или t можно найти координаты точки пересечения.

Далее для удобства заменим нашу систему уравнений на матрицу коэффициентов.

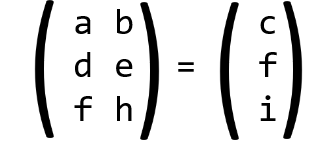
Которую можно схлопнуть.

Дальше все решаем через Крамера, привожу код к решению системы на Python.

# первая прямая
X00 = 2
Y00 = 0
Z00 = 0
X01 = 0
Y01 = 2
Z01 = 0
# вторая прямая
X10 = 0
Y10 = 2
Z10 = 0
X11 = 1
Y11 = 0
Z11 = 2

# вектор первой прямой
DX0 = X01 - X00
DY0 = Y01 - Y00
DZ0 = Z01 - Z00
# вектор второй прямой
DX1 = X11 - X10
DY1 = Y11 - Y10
DZ1 = Z11 - Z10

# компоненты системы
A = DX0
B = -DX1
C = X10 - X00
D = DY0
E = -DY1
F = Y10 - Y00
G = DZ0
H = -DZ1
I = Z10 - Z00

# схлопнем систему ;)
D += A
E += B
F += C
G += A
H += B
I += C


# Принадлежность точки пересечения к первой прямой
def belong0(X, Y, Z):
    Q1 = (X - X00) * DY0
    Q2 = (Y - Y00) * DX0
    Q3 = (Y - Y00) * DZ0
    Q4 = (Z - Z00) * DY0
    return Q1 == Q2 and Q3 == Q4


# Принадлежность точки пересечения ко второй прямой
def belong1(X, Y, Z):
    Q1 = (X - X10) * DY1
    Q2 = (Y - Y10) * DX1
    Q3 = (Y - Y10) * DZ1
    Q4 = (Z - Z10) * DY1
    return Q1 == Q2 and Q3 == Q4


# Определение координат пересечения через параметр s, принадлежности точки пересечения к первой прямой/отрезку
def s_to_p(S):
    X = X10 + DX1 * S
    Y = Y10 + DY1 * S
    Z = Z10 + DZ1 * S
    print(X, Y, Z)
    if belong0(X, Y, Z):
        if belong_section(X, Y, Z):
            print("on section")
            print(X, Y, Z)
        else:
            print("on line, not on section")
            print(X, Y, Z)

    else:
        print("no intersection points, crossing lines")


# Определение координат пересечения через параметр t, принадлежности точки пересечения к первой прямой/отрезку
def t_to_p(T):
    X = X00 + DX0 * T
    Y = Y00 + DY0 * T
    Z = Z00 + DZ0 * T
    print(X,Y,Z)
    if belong1(X, Y, Z):
        if belong_section(X, Y, Z):
            print("on section")
            print(X, Y, Z)
        else:
            print("on line, not on section")
            print(X, Y, Z)
    else:
        X = X01 + DX0 * T
        Y = Y01 + DY0 * T
        Z = Z01 + DZ0 * T
        if belong1(X, Y, Z):
            if belong_section(X, Y, Z):
                print("on section  ASS")
                print(X, Y, Z)
            else:
                print("on line, not on section ASS")
                print(X, Y, Z)
        else:
            print("no intersection points, crossing lines")


def between(A, B, C):
    return A <= B <= C or C <= B <= A


# проверка лежит ли точка пересечения на первом отрезке или на первой прямой, другими словами принадлежность к отрезку
def belong_section(X, Y, Z):
    return between(X00, X, X01) and between(Y00, Y, Y01) and between(Z00, Z, Z01)

det =  D*H - E*G
if det != 0:
    detASS= F*H-I*E
    T = detASS/det
    t_to_p(T)

else:
    v = DX0 * DX1 + DY0 * DY1 + DZ0 * DZ1
    l0 = (DX0**2+DY0**2+DZ0**2)**0.5
    l1 = (DX1 ** 2 + DY1 ** 2 + DZ1 ** 2) ** 0.5
    cos = v / l0 / l1
    if abs(1-cos) < 0.00000000001:
        print("same lines")

    else:
        print(cos)
        print("no intersection points")

Ссылка на полный код на Python && turboprolog 2.0