В прошлых публикациях на Хабре я находил все жилые дома в пешей доступности от входов в метро и МЦК и жилье в 500м от сетевых продуктовых магазинов в Москве.
Когда настал момент объединить все метрики для мегаполиса, включая пешеходные расстояния в единую модель. У меня вышло итоговых 36.5млн кратчайших пешеходных дистанций на расстояния до 2км в городе, не считая тех что отбросил при расчетах. И это только для домов поблизости от метро. Написал многопоточный код и перепробовал множество оптимизаций для чтения исходных домов + точек интереса, записи в базу маршрутов. Эти части программы в итоге завершались за несколько минут, а производительность упиралась в GraphHopper.
Я попопробовал роутинг "многие ко многим" с помощью алгоритма Дейкстры. Этот эксперимент показал что на дорожной сети Москвы он выполнялся медленнее поиска маршрута 1:1 в цикле для тех же начальных и конечных точек. В радиусе 2500м каждое пешеходное расстояние вычислялось на моем ноутбуке около миллисикунды. Расстояния "на сфере" Земли в базе данных рассчитались за 2.5 минуты для 1.4 млн. дистанций в радиусе 500м. Явно что производительность расчета расстояния по прямой и на графе дорог различается на порядки.
Когда пытаешься ускорить вычисления забываешь про тот объем вычислений, который выполняет компьютер по программе, чтобы рассчитать маршруты. Почти любой движок маршрутизации это не просто реализация графового алгоритма поиска кратчайшего маршрута с эвристиками, но еще и учет дополнительных факторов из реального мира при построении маршрута и предпочтений пользователя. В GraphHopper можно указать профиль или матрицу весов, программа учитывает общедоступна ли дорога или частная, тип дороги и тп.
И в этот же день в чате OpenStreetMap RU появляется ссылка на проект, который визуализирует алгоритмы поиска кратчайшего маршрута и еще делает анимацию по шагам на реальных данных OSM прямо в браузере. Поделюсь с вами виртуальной прогулкой из Серебряного бора в Большой театр с помощью honzaap/pathfinding. Эта визуализация алгоритма гораздо нагляднее и применимее другого проекта на JavaScript, потому что использует реальные картографические данные из OpenStreetMap и решает не абстрактную задачу, а вполне реальную и делает это зрелищно.
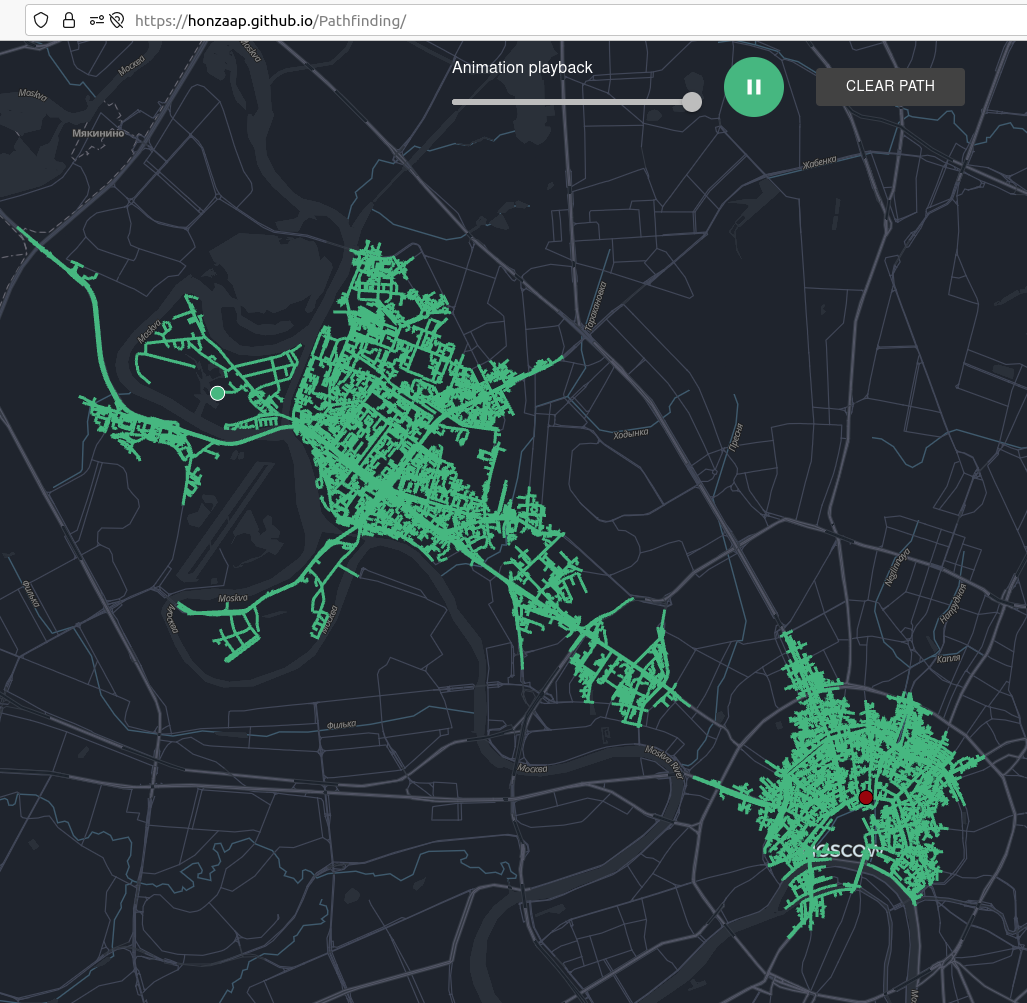
Я иду, шагаю по Москве
Маршрут я выбрал по любимым местам. Маршрут от озера Бездонного до Большого театра это 14 км прогулки на 3 часа:
Старт

Финиш


Как шагают разные алгоритмы
Для этого откроем онлайн версию визуализатора и введем точки маршрута https://honzaap.github.io/Pathfinding/
Первый алгоритм один из самых популярных - это А* алгоритм, графовый алгоритм с эвристикой. На Хабре есть хороший перевод "Введение в алгоритм A*" где рассказывается почему A* быстрее алгоритма Дейкстры.
А* добрался достаточно быстро:
Алгоритм Дейкстры для машрутизации обошел почти четверть Москвы, пока добрался до Большого театра:
Двунаправленный поиск нашел не самый оптимальный маршрут, но обошел меньше улиц чем алгоритм Дейкстры:
Жадный алгоритм быстро нашел как добраться из Серебряного бора в Большой театр
Проект на GitHub
Исходный код доступен https://github.com/honzaap/pathfinding. Для его сборки нужен npm и с помощью vite результат из библиотек и кода собирается в статический html+javascript.
Последняя версия в виде сайта доступна https://honzaap.github.io/Pathfinding/
Алгоритмы могут быть зрелищными
На лекциях по алгоритмам и структурам данных часто монотонный голос лектора нагонял тоску. Но оказывается, если визуально отображать что же происходит в алгоритме на каждом шаге поиска кратчейшего пути в графе, да еще и на данных реального мира, то сразу появляется интерес! Когда сразу видишь задачу которую решает алгоритм и как он это делает. Такие наглядные примеры это именно то, что может заинтересовать учеников.
Комментарии (18)

DarkWolf13
13.11.2023 06:40А если отправить алгоритм от Калининграда до Петропавловска-Камчатского пешком?

igor_suhorukov Автор
13.11.2023 06:40+3Вроде как нет связного графа дорог от Калининграда до Петропавловска-Камчатского
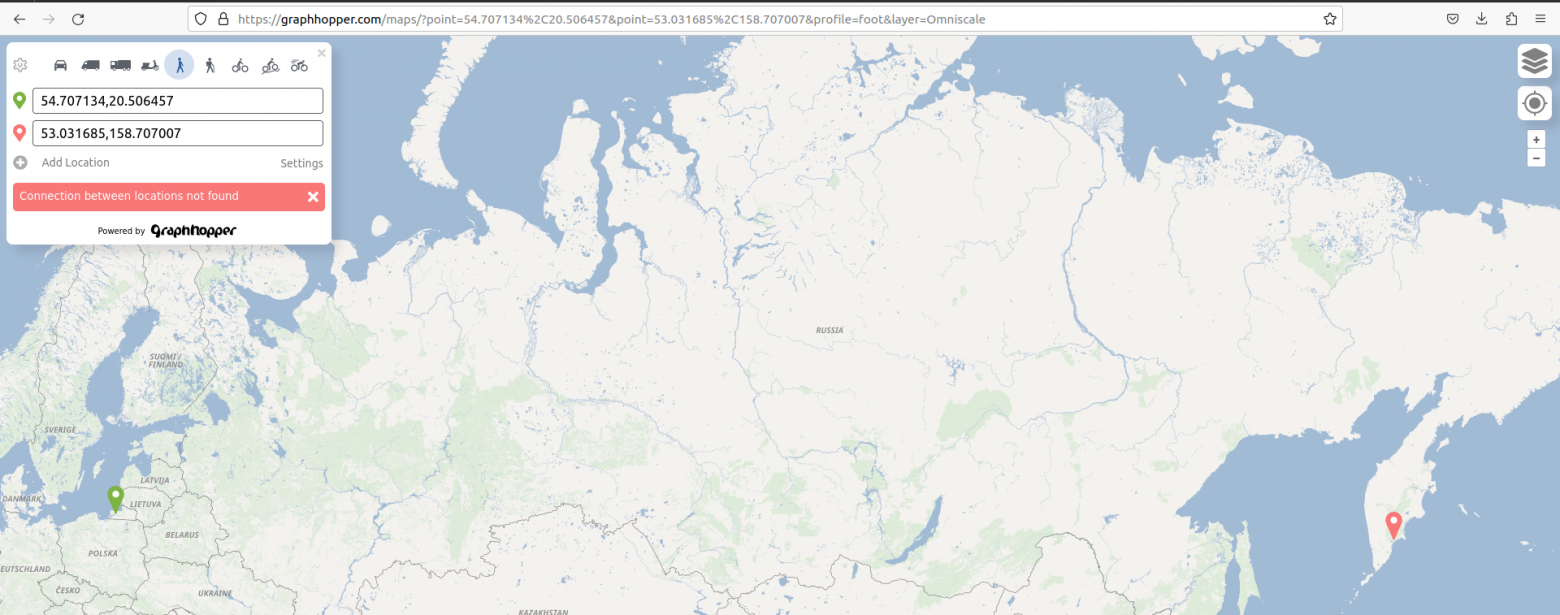
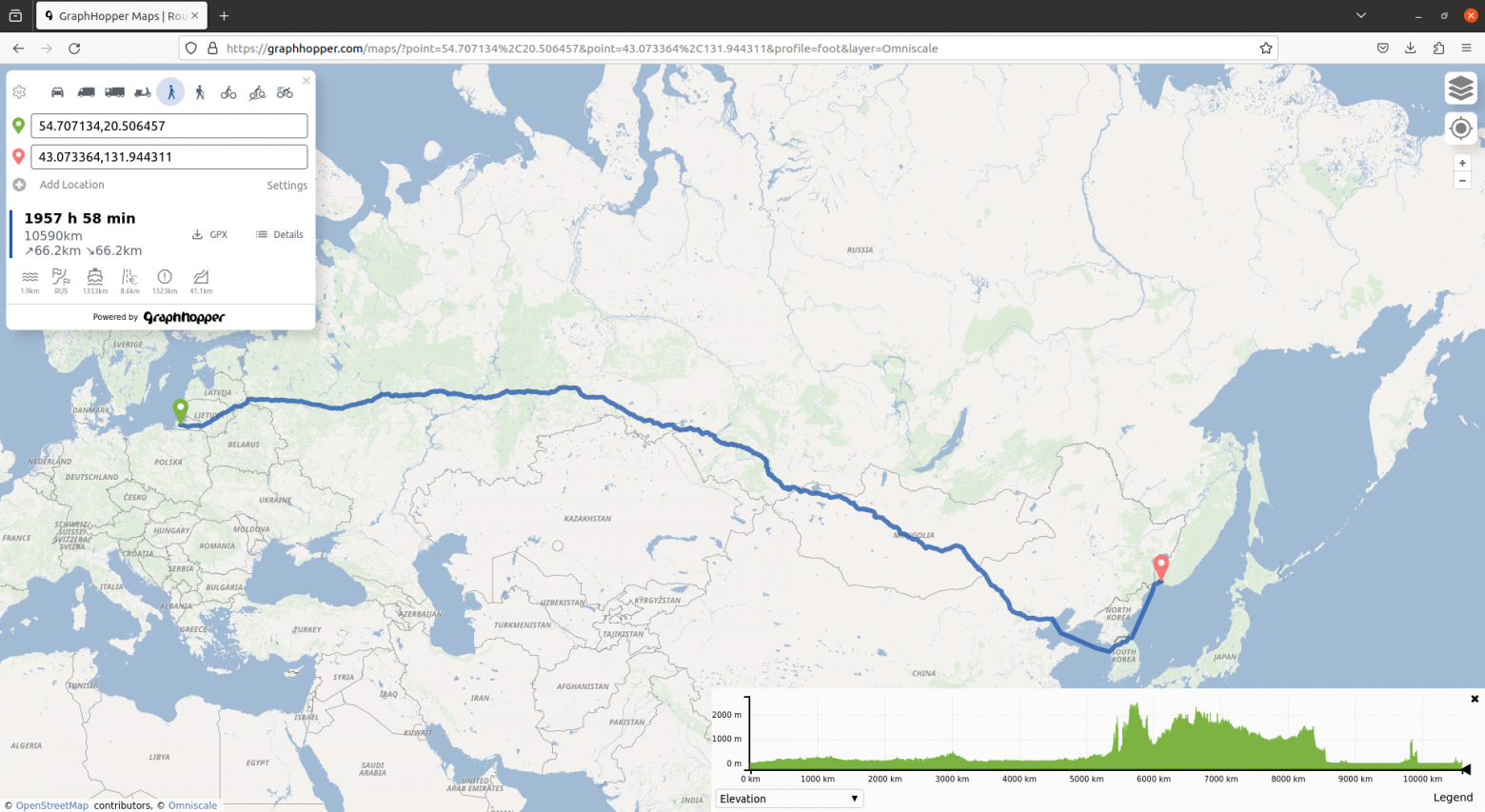
Но при этом можно сходить от Калининграда во Владивосток - это 10590км)

blind_oracle
13.11.2023 06:40Осталось научиться ходить по воде, как один товарищ...

igor_suhorukov Автор
13.11.2023 06:40+1В этом нет смысла, GraphHopper по умолчанию ведет по паромным путям, но это поведение можно переопределить пользовательским профилем и путь станет длиннее и только по суше.

DarkWolf13
13.11.2023 06:40на скриншоте скорее всего какой-то транспортный маршрут.....через монголию....южную корею да еще и морским путем....в том то и загвоздка что дороги, пусть даже и грунтовки есть, только они присутствуют на разных картах и как будто не пересекаются...но если их наложить на один слой и построить сухопутный маршрут.....- сможет ли алгоритм это обработать?

igor_suhorukov Автор
13.11.2023 06:40Месье знает толк в извращениях? Если вам нужен такой маршрут, с теми ограничениями что вы назвали, рекомендую вам изучить документацию GraphHopper и описать требуемый профайл для навигации.
через монголию....южную корею да еще и морским путем
Такие маршруты могут влючать паромные переправы по умолчанию и пересечения границ, в этом скриншоте это: RUS - LTU - LVA - RUS - LVA - RUS - MNG - CHN - KOR - RUS

igor_suhorukov Автор
13.11.2023 06:40+1Алгоритм - это программа, может обработать только те данные что доступны ему на входе. У него нет машинного зрения, возможности просить картографов сделать их работу и прочего. Вводите нужные данные из реальности в входном формате - получаете результат с кратчайшим путем.

WASD1
13.11.2023 06:40Двунаправленный поиск нашел не самый оптимальный маршрут, но обошел меньше улиц чем алгоритм Дейкстры:
Такого быть не должно, если алгоритм написан правильно.
Поиск от финиша проводится на обращённом графе.
igor_suhorukov Автор
13.11.2023 06:40Судя по работе honzaap/pathfinding на данном маршруте, он останавливается на первом пересечении двух подграфов.

WASD1
13.11.2023 06:40Если метод сделан достаточно аккуратно - то первое пересечение и есть оптимальный маршрут (эквилалентный тому, что ищет однонаправленный поиск).
Вероятно по каким-то техническим причинам - двунаправленный поиск сделан недостаточно аккуратно.
freeExec
13.11.2023 06:40Нет это не так. В данном случае получаются найдены минимумы по отдельности для каждого направления, а не общий минимум.
Примерно как треугольник со сторонами 3, 4, 5. По отдельности мы нашли минимумы 3 и 4, и они оба меньше 5. Но в сумме дают 7, а общий минимум 5.

WASD1
13.11.2023 06:40Примерно ... треугольник...
Не знаю что вы имели в виду под "примерно" и "треугольник" (возможно готовы это объяснить строго)?
Вообще же двунаправленный поиск работает так:
Доказывается просто:
Пусть кратчайший путь существует и дискретизируется на нашей карте за T0 = (t0 +dt0) + (t0 - dt0) (лучшее разделение этого пути пополам по времени, в терминах дискретных переходов по нашему графу), то мы его найдём в момент времени t+dt.
(если бы делилось пополам строго (как в упрощённой реализации на уроках в школе) - то мы бы нашли его в момент времени T0/2).*) чисто гипотетически возможны всякие эффекты дискретизации формулы выше, когда: (T1 > T0) && (t1 + dt1 < t0 + dt0) - тогда найдётся путь T1.
Но на практике слишком длинных прямых "выехал на шоссе и едешь пол-часа" стараются избегать просто их разбиением. А в рамках города - наличие таковых вдвойне странно.
Т.е. эффект: "разница в минуту" быть вполне может.
А вот значимой разницы в ответах, тем более в городе, быть не должно.




freeExec
Ждём пулреквест, который научит алгоритм не бежать по встречке. Ну и остальные запреты учитывать. А там глядишь и скорость для эвристики подтянется.
igor_suhorukov Автор
Для этого уже нужен порт OSRM или Вальхаллы на WebAssembly
freeExec
зачем?
igor_suhorukov Автор
Чтобы не превращать демонстрационное приложение в полноценный оттестированный роутер с развесистой логикой. И в случае если нужна навигация именно на github pages в javascript без хостинга бэка.
freeExec
Так мы не делаем полноценный, мы делаем демонстрационный и понятный. Нам не нужна не упаковка данных с быстрым доступом, ни возможности накатывать обновления, пробки нам так же не нужны и все остальные навороты и оптимизации.
igor_suhorukov Автор
Тогда я не отговариваю всех вас делать пул реквесты в honzaap/pathfinding, реализуя на JavaScript логику движка маршрутизации с желаемым функционалом.