Содержание серии статей "Факир математики"

1. Золотое сечение

   1. Первая часть (вы здесь)

   2. Вторая часть

Привет, хабр! На дворе 2023 год. Теперь более чем когда‑либо всё в нашем мире основано на числах. Некоторые из них, как вы уже знаете, имеют собственные имена. Число (пи), число e. Математика везде. Карма и рейтинги в хабре, количество ваших денег, сегодняшняя дата (22.11.2023). Даже есть вид эзотерики, веры — нумерология, вера в том, что числа связаны с судьбой. И ведь все это появилось не на пустом месте.

Мы, будто факиры заклинают своих змей, будем познавать математический мир. Красивый, бездонный и невероятно интересный. Добро пожаловать в серию статей «Факир математики», и тема первой нашей статьи — золотое сечение!

Среди всех замечательных и не очень чисел, цифр есть одно особенно интересное число — 1,6180339887...

Какое‑то обычное, ничем не примечательное число, чуть меньше двойки.

Но оказывается, это число повлияло на большее число блестящих умов, чем пи и e вместе взятые. Список его имен довольно длинный. Это показывает, что к нему относятся с особым благоговением и любовью. Трансцендентное число, золотое число, божественное число и сотни других имен. Мы будем его называть просто — золотым сечением. В математике оно обозначается греческой буквой Ф (фи) и играет в математике и других смежных науках большую роль, обладая удивительными свойствами и очень неожиданными связями с человеком и природой.

Мы начнем с обзора многочисленных применений золотого сечения в науке и искусстве на протяжении всей истории человека. Удивительно, что сквозь века и эпохи, войны и катаклизмы, перемирия и революций столь важное открытие достигло нас. После знакомства с числом Ф мы будем готовы к более глубокому изучению его свойств. Наше путешествие начнется на страницах евклидовых «Начал», и закончится на улицах Флоренции эпохи возрождения, где мы сможем поговорить сквозь века с великим ученым Леонардо да Винчи.

Одним из чудесных свойств золотого сечения является его неисчерпаемая способность порождать изысканные формы — от треугольников до двадцатигранников. Золотое сечение встречается везде.

Но самым удивительным фактом является связь между золотым сечением и абстрактными идеями совершенства, которыми так увлекалось, да и по правде, до сих пор увлекается, человечество.

Развитие многих живых существ следует законам, установленным этим числом, и даже фракталы — красивые симметричные структуры — связаны с золотым сечением.

Золотое сечение

Что общего имеют такие объекты как расположение семян подсолнечника, спираль раковины улитки и млечный путь? Вроде бы они ничем не похожи, и связь с ними очень отдаленная и абстрактная. Какой универсальный геометрический принцип скрыт в работах величайших художников сего мира — от древней античности до нового и новейшего времени? Как бы это просто не звучало, ответом на эти вопросы является просто число, известное на протяжении многих веков, которое постоянно появляется в различных творениях природы и искусства. В результате жизни многих поколений и событий, этому магическому числу были даны различные имена: «золотое число», «божественное сечение» и наиболее известное «золотое сечение». Записать это число практически невозможно, не потому что оно слишком большое (чуть больше единицы), а потому, что оно состоит из бесконечного ряда цифр которые никогда не образуют повторяющуюся группу. Поэтому мы выведем математическую формулу для записи золотого сечения:

Далее мы сможем узнать, как эта незамысловатая формула, которую, может понять даже восьмиклассник, была получена. Но все таки стоит признать, выглядит не впечатляюще. Никакой красоты. Даже связь между числами 1, 5 и 2 не наблюдается. Что получается, автор нас обманул, говорил что золотое сечение это вершина эволюции человечества, а на выходе какая‑то короткая формула с обычными числами? Нет! Внимательный глаз сразу заметит квадратный корень из пяти. Этот корень обладает рядом свойств, которые дали этому числу, как и многим другим подобным, странным названием «иррациональных». Иррациональные числа — это особые числа, на которых мы остановимся и подробно изучим их.

Давайте попробуем подойти к золотому сечению со стороны геометрии, чтобы найти его предполагаемое божественное свойство. Для этого построим прямоугольник, одна сторона которого в 1,618 раз длиннее другой. Получится прямоугольник, в котором соотношение сторон представляет собой золотое сечение.

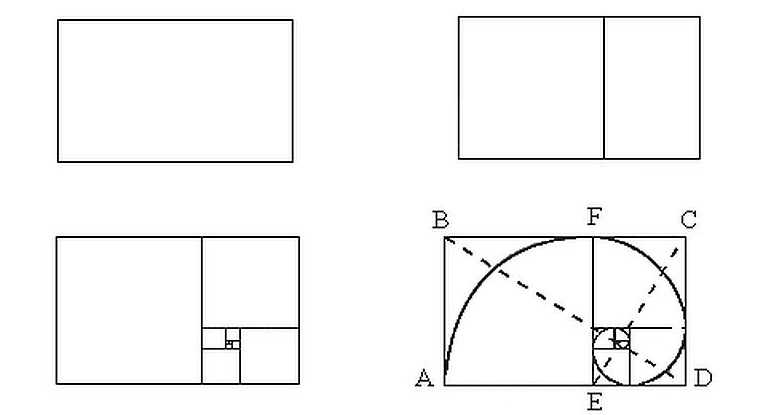
Прямоугольник с таким соотношением сторон называют золотым. На первый взгляд он может показаться нам обычным прямоугольником. Но есть одно интересное свойство. Если положить два одинаковых золотых прямоугольников, один горизонтально, а другой вертикально так, чтобы их нижние стороны находились на одной линии, и провести диагональную прямую и продолжить ее, то можно будет увидеть, что она пройдет в точности через правый верхний угол вертикальной другого прямоугольника — интересная и приятная неожиданность. Это свойство является характерным для двух золотых прямоугольных объектов одинакового размера. Многие повседневные прямоугольные объекты созданы именно с таким соотношением размеров. Случайность или заговор математиков?Может быть и то и то. Или, возможно, такие прямоугольники и другие геометрические фигуры, использующие золотые сечения, по каким‑то причинам приятны глазу. Согласившись с таким суждением, мы разделим мнение не только пару математиков, но и всех величайших художников и архитекторов. Не случайно в математике золотое сечение обозначают именно буквой фи (Ф), первой буквы имени знаменитого греческого скульптора Фидия.

Этот прекрасный золотой мир

Мало кто не слышал о знаменитой таинственной картине с Моной Лизой. Наложим на картину несколько золотых прямоугольников.

Флорентийский гений, может, и не думал о золотом сечении, работая над своим произведением, но одно ясно точно — он придавал большее значение связи между красотой и математикой. Интересно, что Леонардо да Винчи делал иллюстрации к математической книге "De Divina Proportione" («О божественной пропорции»), написанной его хорошим другом Лукой Пачоли.

Леонардо, естественно, не единственный художник, в чьих работах встречается золотое сечение как в виде отношения двух сторон прямоугольника, так и в более сложных геометрических формах. Этот принцип в своих работах соблюдали художники следующих поколений. В экстраординарной работе «Тайная вечеря» Сальвадора Дали, которая рассказывает о библейском сюжете, когда Иисус узнал, кто его продал за 30 серебренников, тоже есть золотое сечение, и оно играет не последнюю роль. Как таинственно, и это ведь простое число... Да и в «Тайной вечере» есть не только золотой прямоугольник, но и сама картина имеет размер 268 на 167 сантиметров (почти идеальный золотой прямоугольник), а также изображен монументальный додекаэдр, восьмигранник. Эта фигура является одним из правильных многогранников, которые можно вписать в сферу, и тесно связана с золотым сечением.

Давайте теперь обратимся не к художественному искусству — а к вершине прикладного искусства — уже догадались, о чем речь? Об архитектуре.
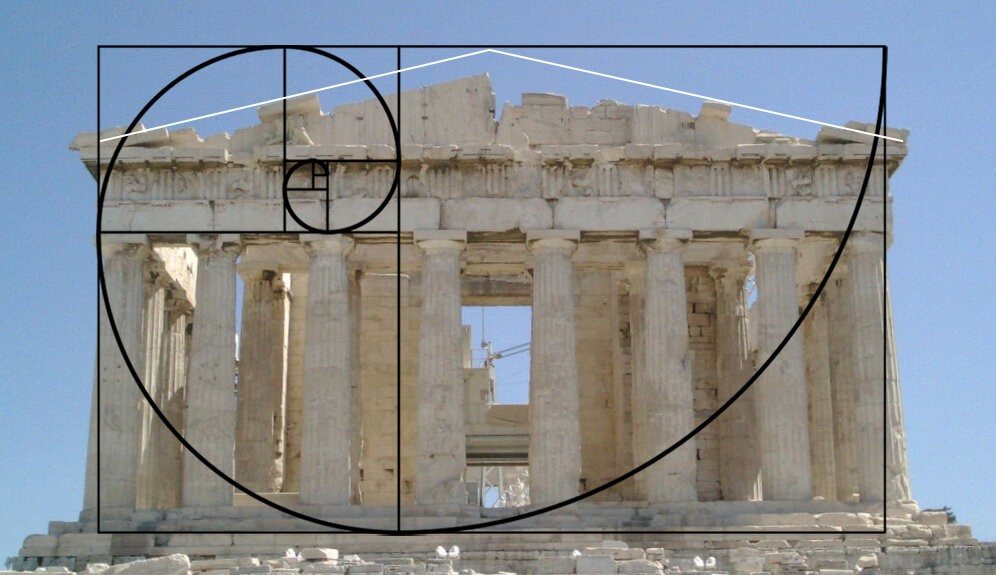
Если золотое сечение и вправду создает некую гармонию во всех ее проявлениях, то, возможно, мы увидим это в геометрических фигурах и формах самых известных в мире зданий.
Особенно это видно в одном из самых величайших творений Фидия — храм Парфенона. Например, различные элементы фасада Парфенона, представляют собой золотые прямоугольники.

Розы, в чем же ваш секрет?

Связь золотого сечения с красотой — вопрос не только человеческого восприятия. Похоже, сама природа наделила Ф особыми свойствами и выдала особую роль. Давайте углубимся в свойства золотого сечения, чтобы понять эту особую роль. Возьмем уже знакомый золотой прямоугольник и впишем в него квадрат, стороны которого равны ширине нашего прямоугольника. Повторим эту процедуру и проведем дугу в каждом из квадратов.

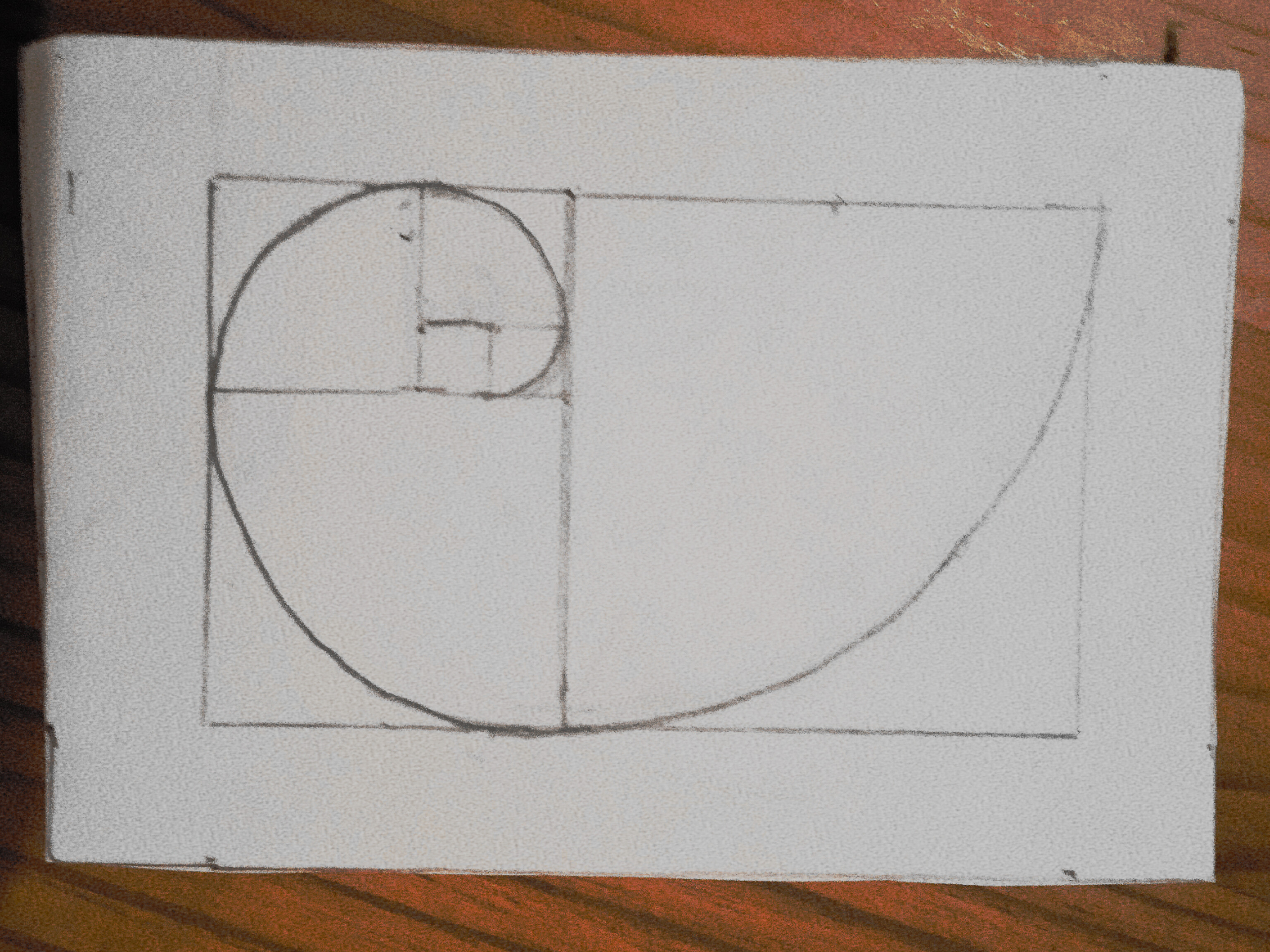
Эта элегантная кривая называется логарифмической спиралью. Она вовсе не является математическим курьезом, наоборот, это волшебная линия часто встречается в физическом мире.

На примере королевы цветов и символа Англии — розы, мы вступаем во владения природы. Присутствие золотого сечения здесь неочевидно и требует введение нового математического понятия: последовательности Фибоначчи. Это последовательность чисел, описанная итальянским (опять) математиком в 13 веке, начинается с двух единиц, а каждое следующее число равно сумме двух предыдущих. Вот первые пятнадцать чисел этой бесконечной последовательности:

Частное от деления любого числа последовательности Фибоначчи на предшествующее ему число будет стремиться к Ф, давая все более точное значение для каждого следующего числа последовательности:

1 / 1 = 1
2 / 1 = 2
3 / 2 = 1.5
5 / 3 = 1.666...
8 / 5 = 1.6
13 / 8 = 1.625
21 / 13 = 1.615348
34 / 21 = 1.61904
55 / 34 = 1.61764
89 / 55 = 1.61818
144  89 = 1.61797

Ф = 1.6180339887

Для сорокового числа последовательности частное совпадает с золотым числом с точностью до четырнадцатого десятичного знака. Связи между золотым сечением и числами Фибоначчи многочисленны и неожиданны, позже мы их рассмотрим более подробно. Достаточно пока отметить, насколько невероятна эта связь между абстрактным царством чисел и физической реальностью.

Числа, числа и еще раз числа

Каким бы стал наш мир, если бы однажды легли спать, а ночью все числа, цифры и сама математика исчезли бы, испарились не оставив следа. На следующий день мы проснулись бы в мире без ПК, без радио и телевидения, без JavaScript и — о нет, — без хабра.

А что творилось бы на улице! Человеческое общество не может существовать без чисел. Их значение невозможно переоценить. Числа отражали и направляли человеческую деятельность с доисторических времен, и, пожалуй, они являются фундаментом человеческой цивилизации. Невероятно твердым фундаментом, которые выдерживает всю тяжесть людей.

Все нации и цивилизации создавали свои системы счисления, и в каждой культуре это происходило по‑разному. Тем не менее все числа имели одни и те же функции: счет, упорядочивание, измерение и кодирование.

Конец... Или нет?

Статья подходит к концу. В этой статье мы узнали о последовательности Фибоначчи, золотом сечении, как рисовать золотой прямоугольник, что такое числа.

Мы приоткрыли завесу красоты золотого сечения. Но нам предстоит узнать, почему 0 — самое важное число, в чем состоит иррациональность квадратного корня из двух, об Евклиде, и зайдем в золотую математику. Все это предстоит в следующих статьях. Если вам понравилась данная публикация, и вы хотите продолжения, то ставьте плюсы и оставляйте комментарии.

С вами был доктор Аргентум, и это — только начало глубокого изучения математики!

Напоследок: число Ф с 1000 числами после запятой

Ф = 1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362