В этой серии статей я стараюсь сделать видимыми и ощутимыми некоторые элементы теории хаоса, которой я занимался профессионально несколько лет назад. В предыдущих частях этой серии (Часть 1, Часть 2) мы увидели каким образом рождается странный аттрактор в предельно простой гамильтоновой системе — шарике, прыгающем на подпружиненном столике. Эта система способна порождать и красивые картинки и красивые объяснения этим картинкам. Сейчас мы рассмотрим некоторые качественные и количественные характеристики странных аттракторов.

Я вынужден был сделать большой перерыв между публикациями, так что рекомендую освежить в памяти предыдущие части серии, к тому же, там есть симпатичные картинки и анимации (берегите трафик!).

Показатели Ляпунова

Главное качественное свойство странного аттрактора и связанного с ним динамического хаоса — это перемешивание фазового пространства и связанное с ним экспоненциально растущее расстояние между близкими точками. Давайте посмотрим на это явление, построив график зависимости расстояния между какими‑то двумя точками от количества итераций отображения Пуанкаре нашей системы для трёх типов орбит: неподвижной точки (полюса пятого порядка, который показан зелёными точками), инвариантного тора (красная замкнутая орбита) и странного аттрактора (туман голубых точек).

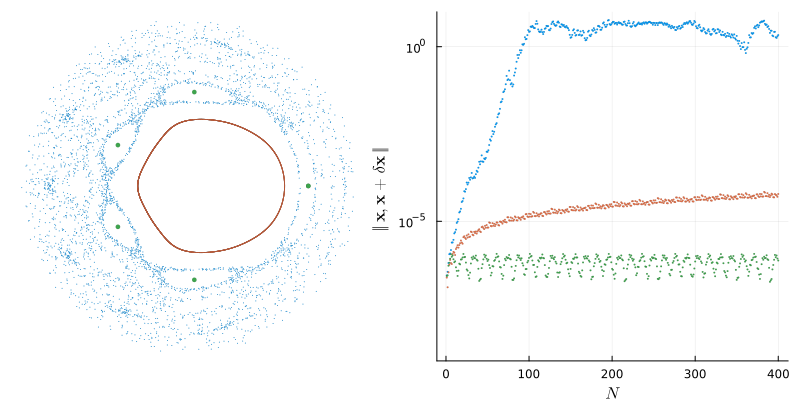
Нас не должно смущать то, что вокруг неподвижной точки тоже происходит изменение расстояния между соседями: в нашем эксперименте, выбирая соседей, мы неизбежно промазываем мимо полюса. Это приводит к периодическим колебаниям расстояния, но оно не растёт со временем.

В окрестностях инвариантного тора соседние точки тоже постепенно разбегаются. Это связано с тем, что каждый тор имеет своё число вращения и соседние точки, оказавшись на соседних торах, будут двигаться с разной скоростью и удаляться друг от друга. Причём скорость удаления будет не экспоненциальной, а близкой к линейной, что мы и наблюдаем на графике в логарифмических координатах, как некоторую логарифмическую кривую.

Наконец, окрестности точек странного аттрактора ведут себя также как окрестности седловых точек: растягиваются и сжимаются, следуя геометрической прогрессии. Это растяжение и отражает положительный наклон линии роста расстояния. В логарифмических координатах экспоненциально растущая кривая выглядит прямой, а её наклон отражает показатель роста. Можно усреднить скорость разбегания соседних точек по всей орбите, получив таким образом характеристику не отдельной точки, а всей орбиты в целом.

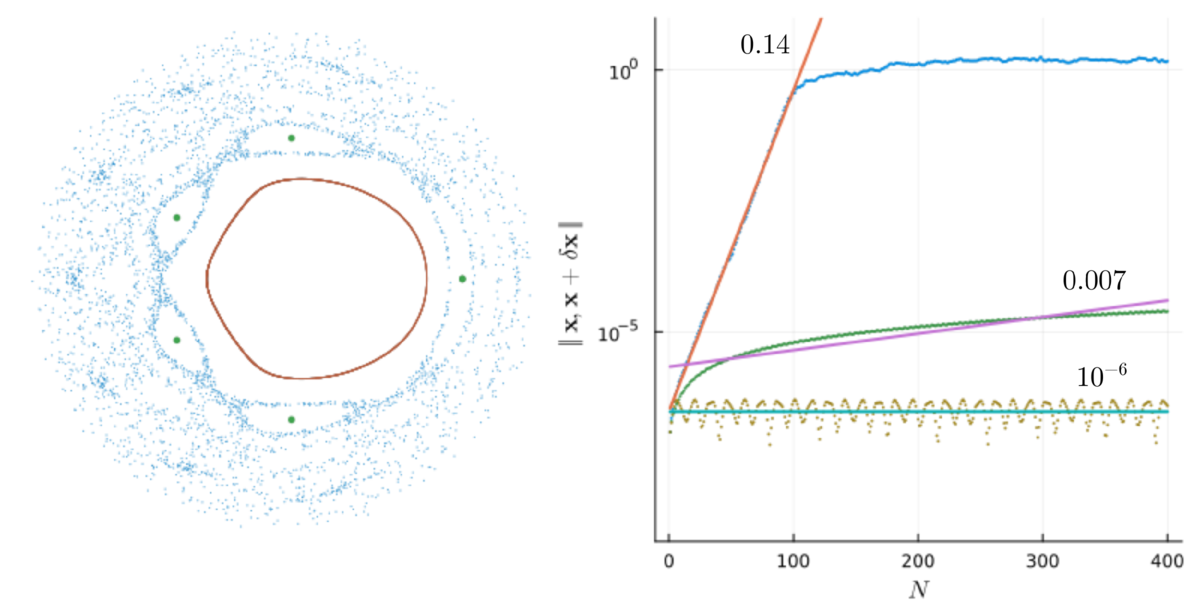
Для изучения динамики системы в окрестности неподвижных точек мы использовали матрицу Якоби — аналог производной для вектор-функции, а именно, вычисляли собственные числа этой матрицы. Как показал Сэмюэль Смейл, странный аттрактор состоит из бесконечного множества неподвижных точек разного порядка, однако всё они оказываются неустойчивыми. Для характеризации не отдельных неподвижных точек, а всего аттрактора в целом, используется модифицированный спектр, состоящий из чисел, называемых показателями Ляпунова. Количество показателей совпадает с размерностью фазового пространства и каждый из них соответствует темпу экспоненциального разбегания траекторий вдоль каждой из обобщённых координат. Однако, имеет смысл вычислять эту скорость не вдоль координат, а вдоль тех направлений, вдоль которых изменения расстояний между точками будет максимальным. Такие числа вычисляются на базе якобиана, по относительно несложному алгоритму, который не только усредняет скорость разбегания соседних точек вдоль траектории, но и собственные направления этого разбегания. Те усреднённые наклоны графиков для расстояния между соседними точками от числа итераций, что мы видели, соответствуют максимальным показателям Ляпунова. Со временем именно эти показатели будут доминировать и наблюдаться в динамике системы.

И тут есть один нюанс. В диссипативных неавтономных системах (в которых есть потери энергии и внешняя энергетическая подпитка) ляпуновские спектры устойчивых траекторий: неподвижных точек и предельных циклов, имеют только отрицательные показатели. Наличие в спектре траектории хотя бы одного положительного показателя подсказывает, что эта траектория может иметь хаотические свойства. Однако наша система консервативна, это приводит к тому, что все отображения строго сохраняют фазовый объём, деформируя его, но оставляя его меру неизменной. Это значит, что показатели Ляпунова в гамильтоновых системах обязаны появляться парами: . Следовательно, в таких системах как наша, положительные показатели неизбежны для любых нетривиальных траекторий, разница только в величине положительного показателя. Наш предыдущий эксперимент показал, что показатели для разных типов орбит отличаются существенно.

Вот как меняется максимальный показатель Ляпунова (LLE), вычисленный для различных траекторий при изменении энергии системы.

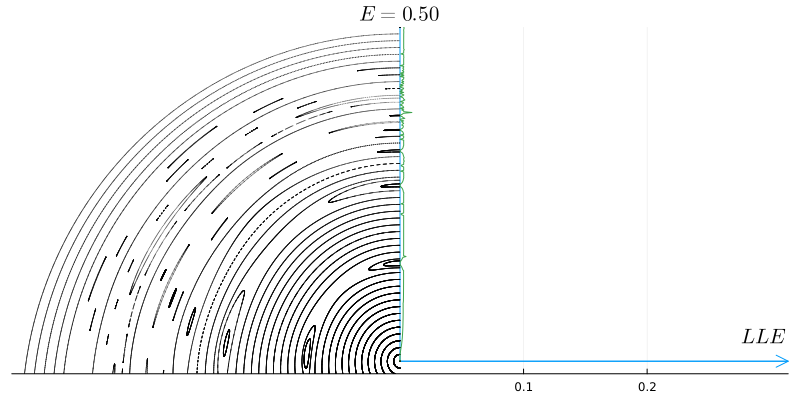
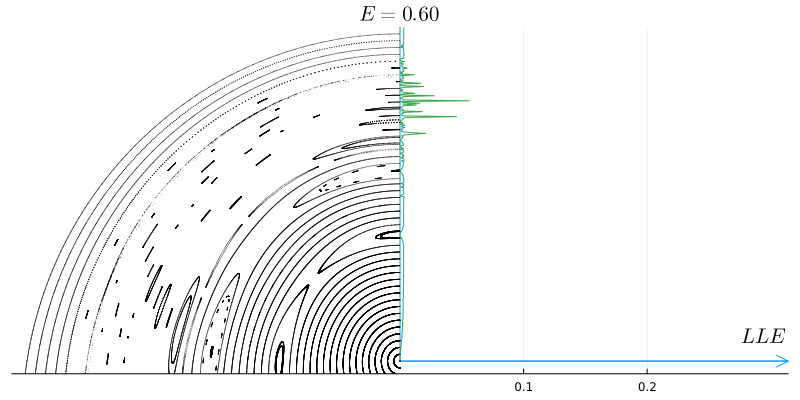
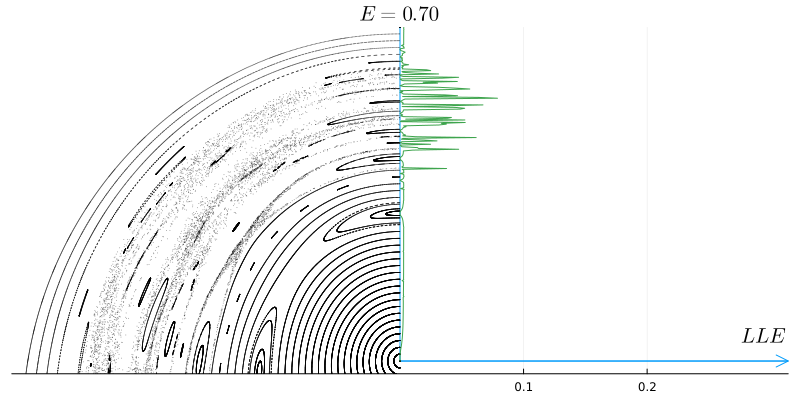
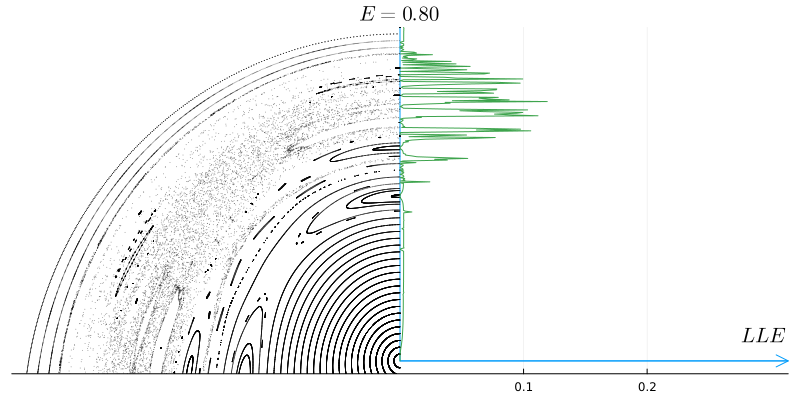
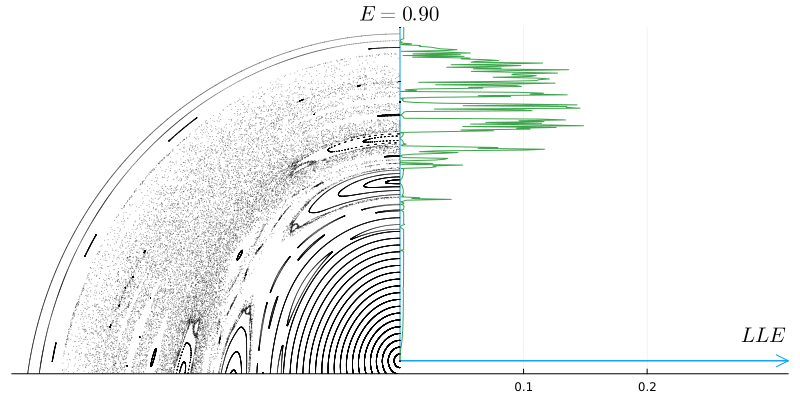
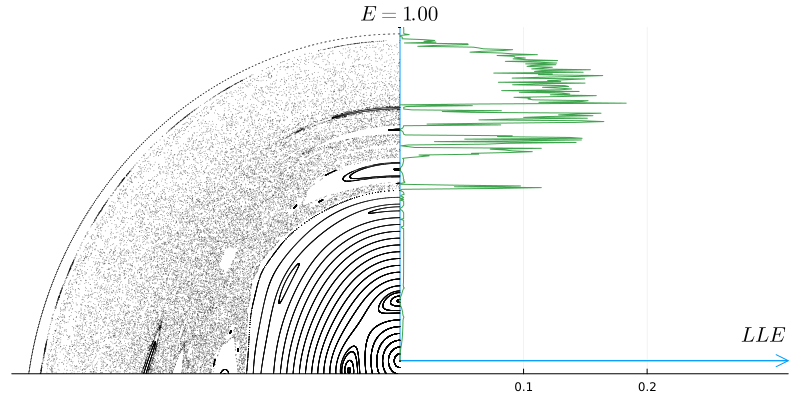
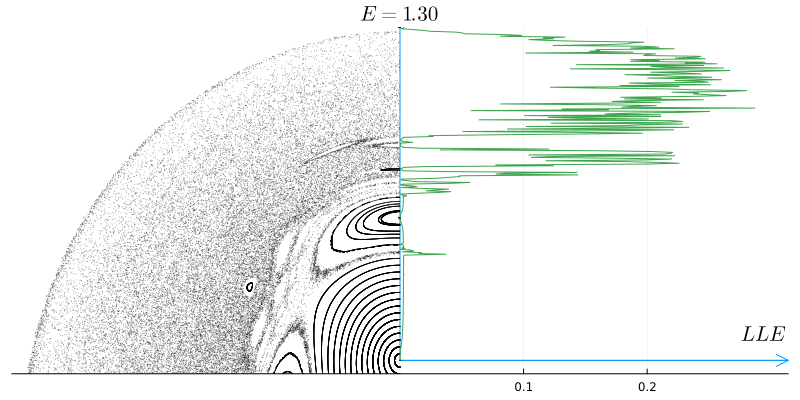
Теперь совершенно очевидно, что полюсы исключительно стабильны, инвариантные торы имеют очень малые значения максимального показателя Ляпунова, а хаос резко проявляется ростом максимального показателя.

Показатели Ляпунова имеют размерность, обратную времени или числу итераций для дискретного отображения. Это позволяет рассматривать их как характерную скорость забывания системой начального состояния или как темп потери информации в системе. Величина, обратная максимальному показателю Ляпунова, называется временем Ляпунова. Его можно вычислить для многих природных процессов, получая информацию о том в каких временных интервалах имеет смысл прогнозировать поведение системы, исходя из наблюдаемых параметров состояния. Так, например для Солнечной системы это время составляет 5 млн лет, а для погоды на Земле оно имеет порядок пары недель. Как видим, наш прыгающий шарик способен забывать свои начальные условия всего лишь за 5–10 шагов.

Мы рассматривали показатели Ляпунова как характеристики динамической системы и её траекторий или орбит. Но не являются ли они, в первую очередь, характеристиками вычислительных процессов, которые мы использовали для моделирования динамики нашей системы? Иными словами, не исследуем ли мы вместо системы метод Ньютона, с помощью которого вычисляются моменты соударений?

Вот как меняется оценка максимального показателя Ляпунова при использовании разной точности вычислений.

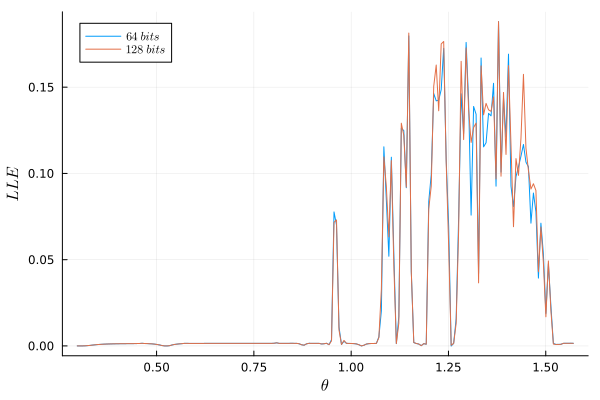
Этот эксперимент показывает, что наша математическая модель вполне соответствует описываемому явлению.

Фрактал Ляпунова

Показатели Ляпунова позволяет нам увидеть на одной диаграмме два механизма приводящих к появлению странных аттракторов: разрушение гетеро- и гомоклинических орбит, а также каскад бифуркаций удвоения периода. Наша система очень простая (поэтому я её и выбрал в качестве примера), для полного описания всей её динамики достаточно всего двух параметров: энергии системы  и начальной точки орбиты. Таким образом, максимальный показатель Ляпунова позволяет нам увидеть динамику системы в пространстве всех её параметров , и различить полюсы, инвариантные торы и странные аттракторы. Так на одной карте можно увидеть всё динамические процессы системы и сценарии перехода к хаосу. Вот она:

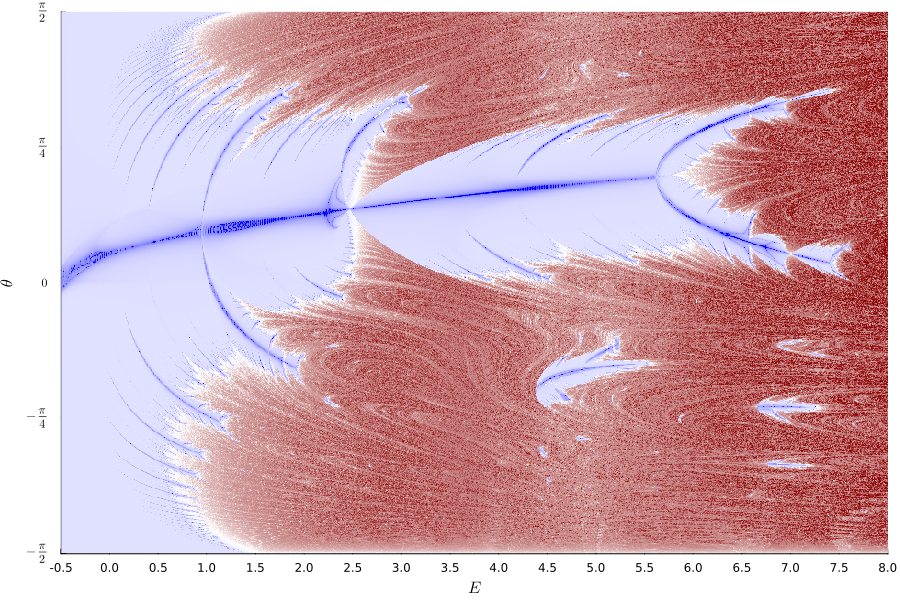
Синий цвет на этой диаграмме соответствует устойчивым орбитам: полюсам и их окрестностям. Голубой цвет — инвариантным торам. Наконец, серые и коричневые области обозначают странные аттракторы. Рассмотрим несколько частей этой диаграммы внимательнее.

Обратите внимание на то, что внутри серо-коричневой хаотической области проявляются некоторые собственные структуры: островки стабильности и то что геологи или петрографы назвали бы флюидальной текстурой, похожей на фигуры течения или пластических деформаций. Это говорит о том, что странный аттрактор порождает не просто случайный набор точек, его беспорядок обладает собственной внутренней структурой, плавно и непрерывно меняющейся при изменениях параметров системы.

Рождение резонансов

Первым на диаграмме бросается в глаза глубокий стабильный жёлоб, порождённый неподвижной точкой . От него по мере увеличения энергии отходят длинные синие «когти» полюсов более высоких порядков. Вот как выглядит первое появление хаоса в системе:

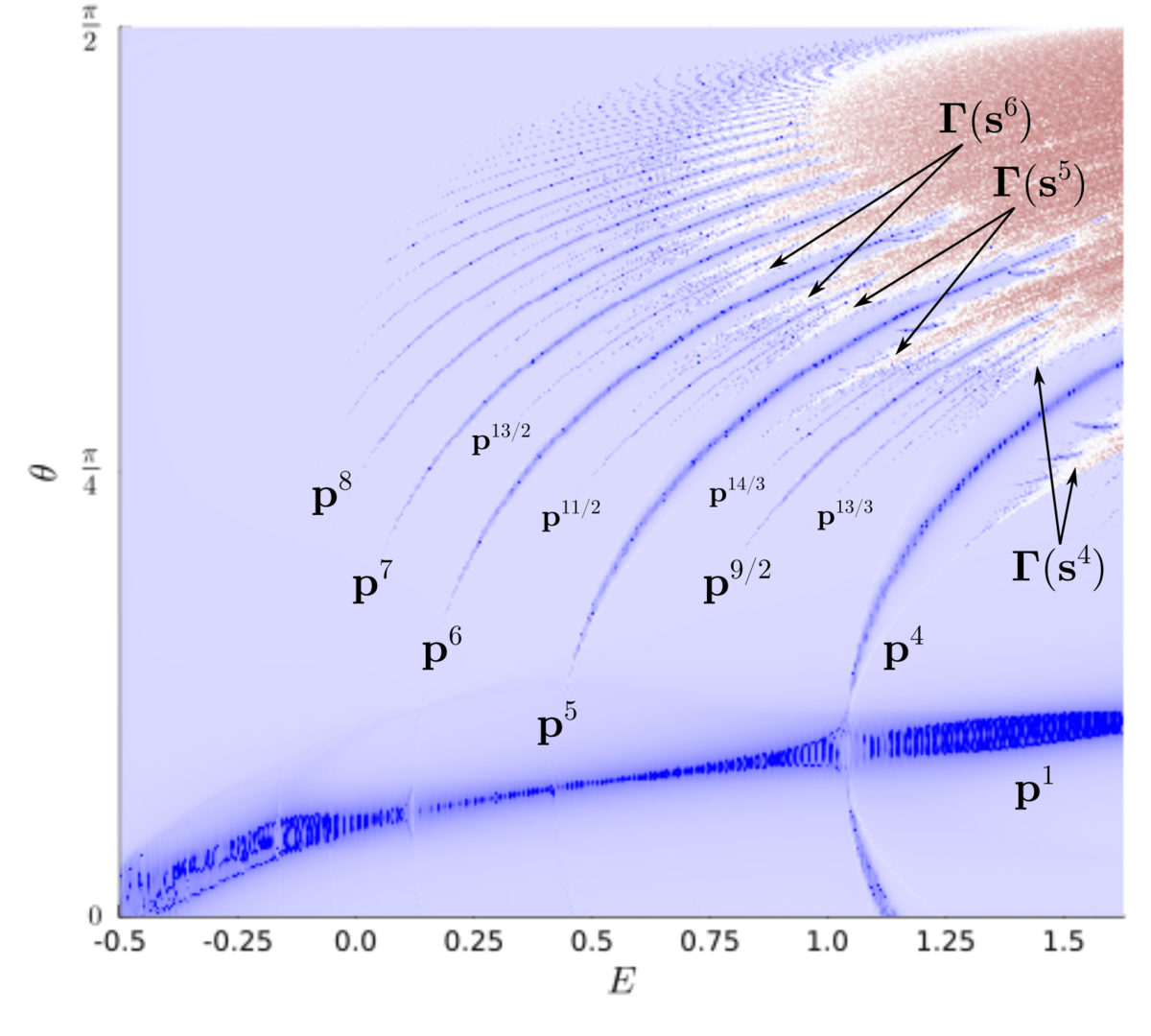
Во взаимном расположении полюсов без труда читается структура множества рациональных чисел (дерево Штерна-Броко), которое соответствует структуре чисел вращения резонансов.

От каждого полюса отходит тонкий, постепенно расширяющийся неустойчивый «хребет» порождённый гетероклиническими орбитами седловых точек. На диаграмме они отмечены буквами , с указанием соответствующих седловых точек. Соединяющие седловые точки орбиты разрушаясь, порождают странные аттракторы, которые постепенно расширяются, демонстрируя явление диффузии Арнольда.

Линии полюсов небольшого порядка глубоко врезаются в хаотическую область, создавая в ней заливы, которые в странном аттракторе мы видим, как острова порядка в море хаоса. Увеличение энергии приводит к тому, что полюсы тоже начинают порождать резонансы более высоких порядков. Это придаёт бифуркационной диаграмме самоподобие и фрактальную структуру.

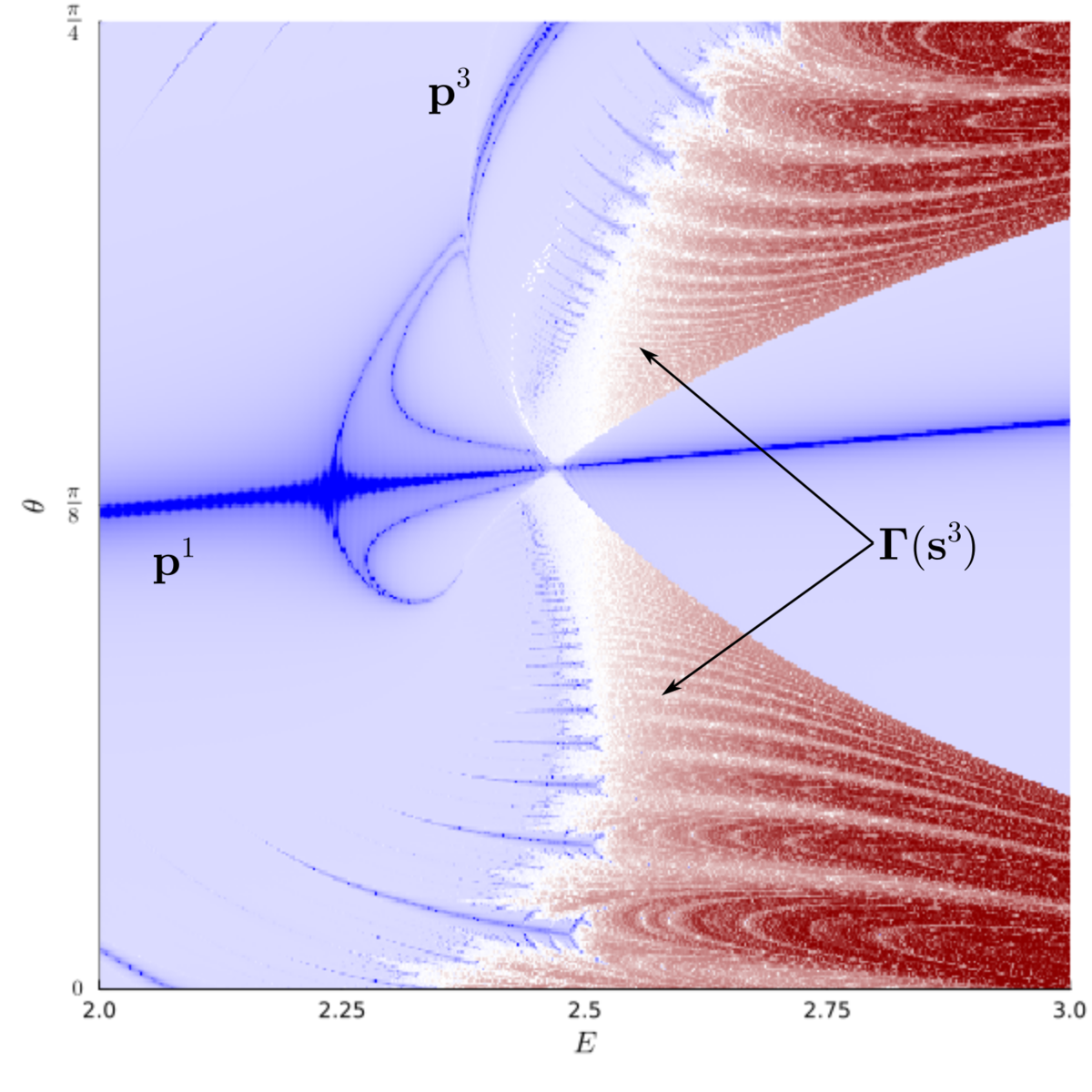
Очень любопытную картину показывает область рождения резонанса . Его рождению предшествует нарастающее возмущение полюса , и появление множества резонансов высокого порядка. Одновременно с полюсом рождается и седловая точка , гетероклиническое многообразие которой незамедлительно разрушается и порождает расходящуюся хаотическую область. Однако теперь становится видно, что диффузия Арнольда происходит за счёт появления и исчезновения множества полюсов и сёдел очень высокого порядка, окружающих седловую точку.

Удвоение периода

Наконец, в тех местах, в которых заливы устойчивости заканчиваются, уступая место хаосу, происходит каскад рождений резонансов, заканчивающийся удвоением периода полюса. Так происходит "растворение" полюса в странном аттракторе. Архетипичный случай демонстрирует полюс :

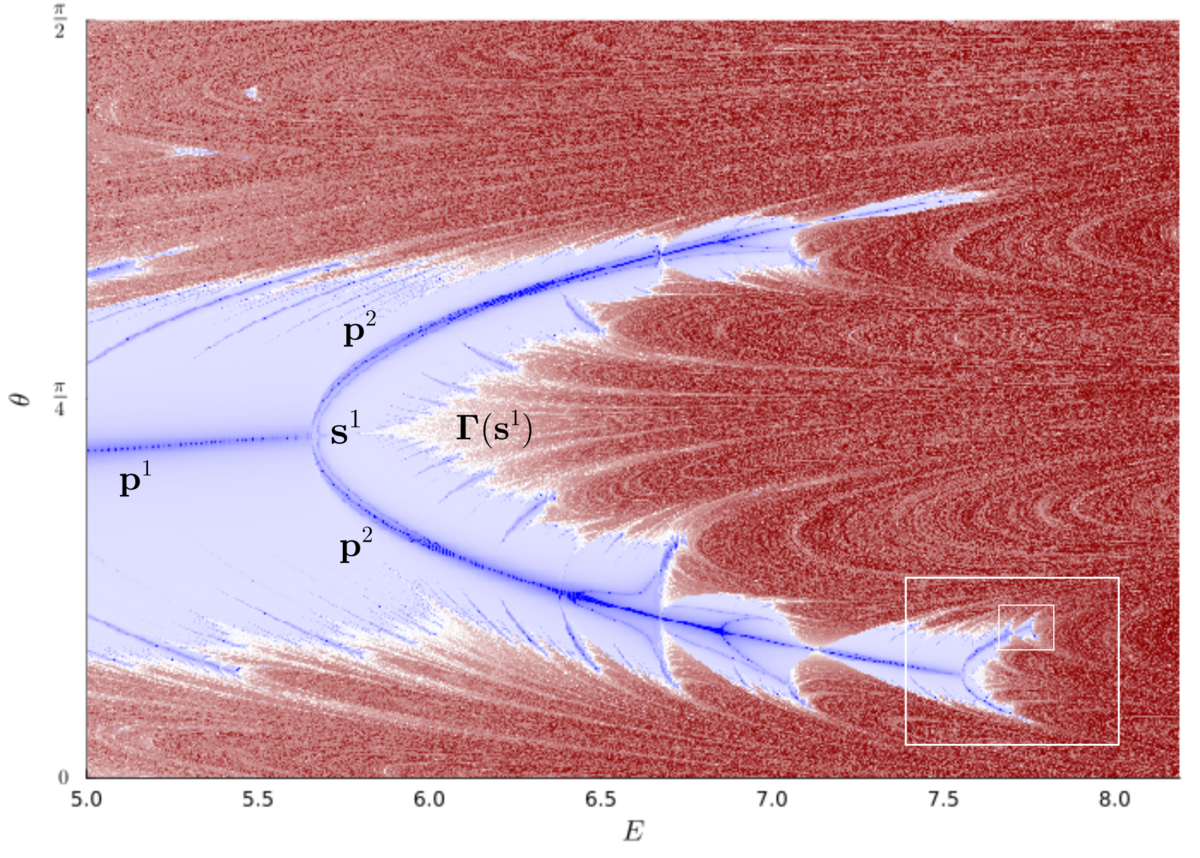
В точке бифуркации неподвижная точка превращается из полюса в седловую , и порождает пару новых полюсов второго порядка . Гомоклиническая орбита , соединяющая точку с самой собой разрушается, порождая странный аттрактор, поглощающий полюса более высокого порядка. Эту же судьбу повторяют и полюсы , как показано внутри выделенного прямоугольника. Новые полюсы вскоре вновь испытывают удвоение периода (ещё меньший прямоугольник) и очень быстро поглощаются хаосом. Этот же сценарий наблюдается на всех масштабах для всех полюсов. Даже в небольшом упорядоченном островке, который порождается полюсом , мы вновь наблюдаем ту же череду бифуркаций.

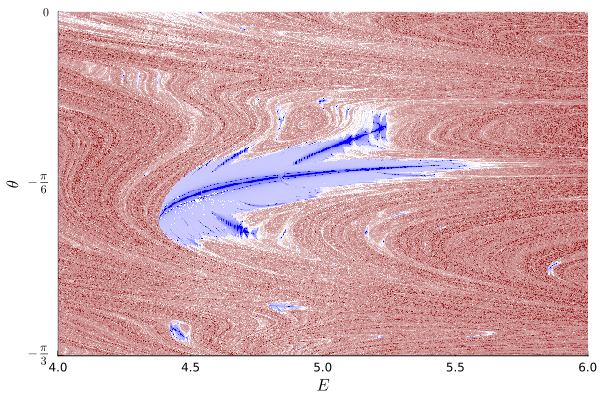
Мы использовали для построения диаграммы нулевой меридиан на сферической поверхности постоянной энергии системы. В силу физической симметрии на нём должны располагаться все неподвижные точки. Однако области инвариантных торов распространяются далеко за пределы нулевого меридиана и способны, деформируясь, пересекать его вновь, что мы и видим, как внезапно появляющиеся островки порядка.

Напоследок, классическим образом продемонстрирую самоподобие бифуркационной диаграммы, увеличивая приближение к точке, в которой каскад удвоений периода  приводит к глобальному хаосу.

Большая анимированная картинка

Спектральные характеристики

Обсуждая сценарии перехода к хаосу, мы неоднократно использовали частотные характеристики траекторий и орбит: периоды неподвижных точек, числа вращения инвариантных торов и переход к хаосу через последовательность бифуркаций удвоения периода. Всё эти вещи мы анализировали, работая в фазовом пространстве, которое практически не содержит временных зависимостей. Сейчас имеет смысл взглянуть на преобразования Фурье для временных рядов. Как и с показателями Ляпунова, взглянем сначала на спектры отдельных типов траекторий: полюсов разных порядков, инвариантных торов и странного аттрактора.

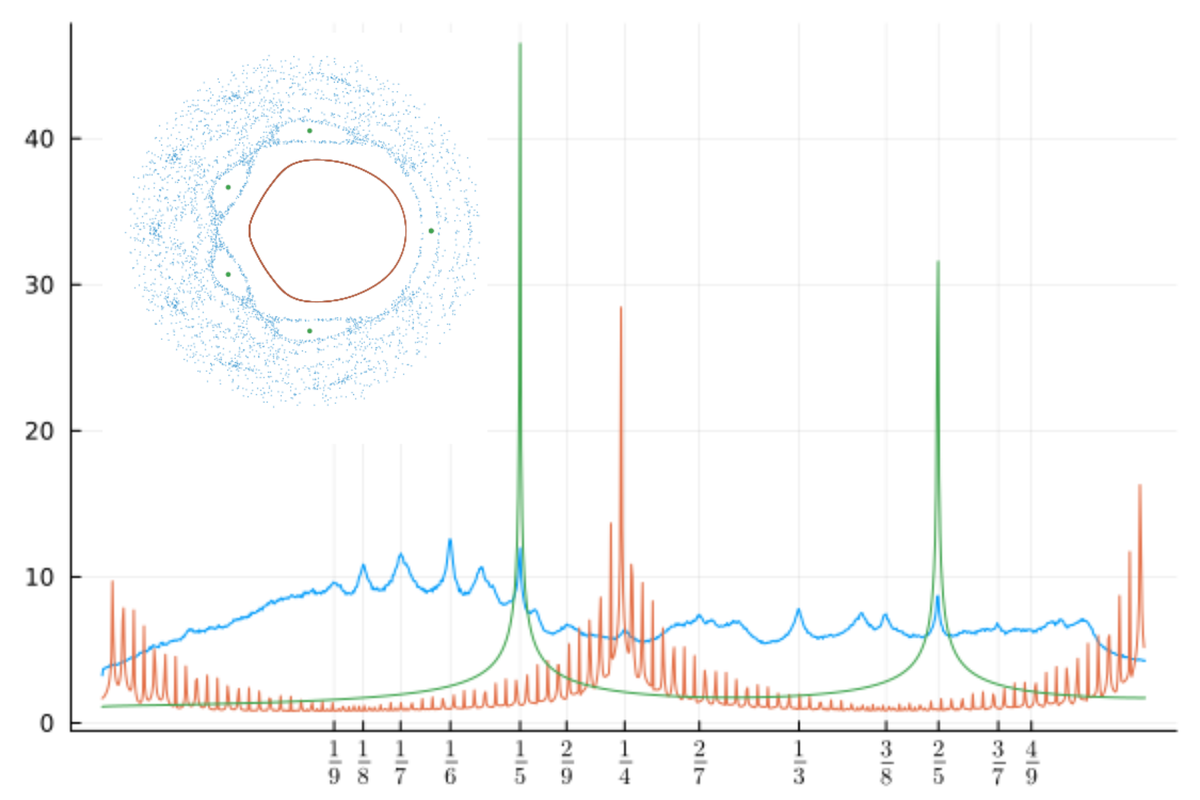
Частоты в этих спектрах соответствуют числам вращения, именно их мы и видим в качестве пиков на спектрах. Полюс  ожидаемо представлен кратными пиками с частотами 1/5 и 2/5. Спектр инвариантного тора имеет не только пики около 1/4, но и целую «гребёнку» вторичных пиков, которая соответствует резонансу очень высокого порядка.

Спектр странного аттрактора сильно отличается от спектров регулярных орбит тем, что он сплошной, а не линейчатый и содержит все частоты от низких до высоких, приближаясь к шуму. Однако на фоне этого шума выделяются пики с частотами, имеющими небольшие знаменатели, которые соответствуют нескольким первым слоям дерева Штерна-Броко, (мы говорили об этом, рассуждая о резонансах). Интересно, насколько универсальны эти свойства странных аттракторов: сплошной спектр и наличие рациональных частот с малыми знаменателями?

Объединив спектры для отдельных траекторий, мы получим спектрограмму для всего семейства орбит системы при заданной энергии. Так что у нас появляется возможность взглянуть на все странные аттракторы для заданной энергии.

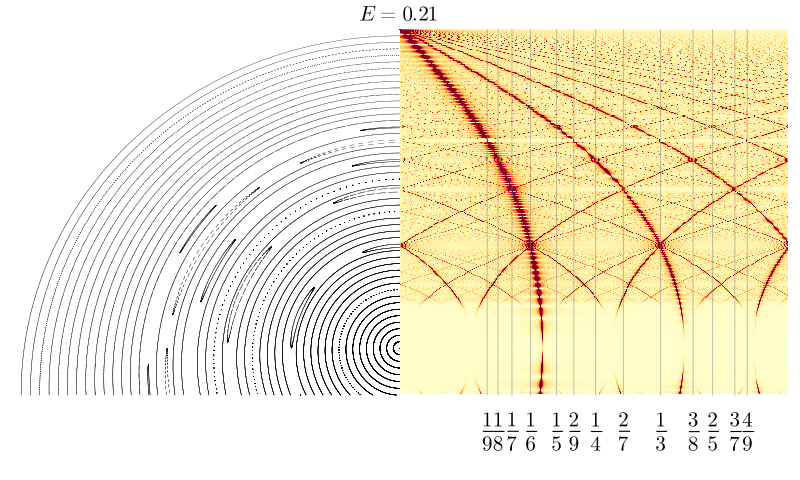
Первым делом, обратим внимание на то, как при малых энергиях формируются резонансы в точках пересечения линий, соответствующих числам вращения с небольшими знаменателями. Такую же картину можно наблюдать в геометрической демонстрации устройства дерева Штерна-Броко, которая называется диаграммой Фарея. Сравните левую половину этой диаграммы с основными частотами, выделяющимися на спектрах.

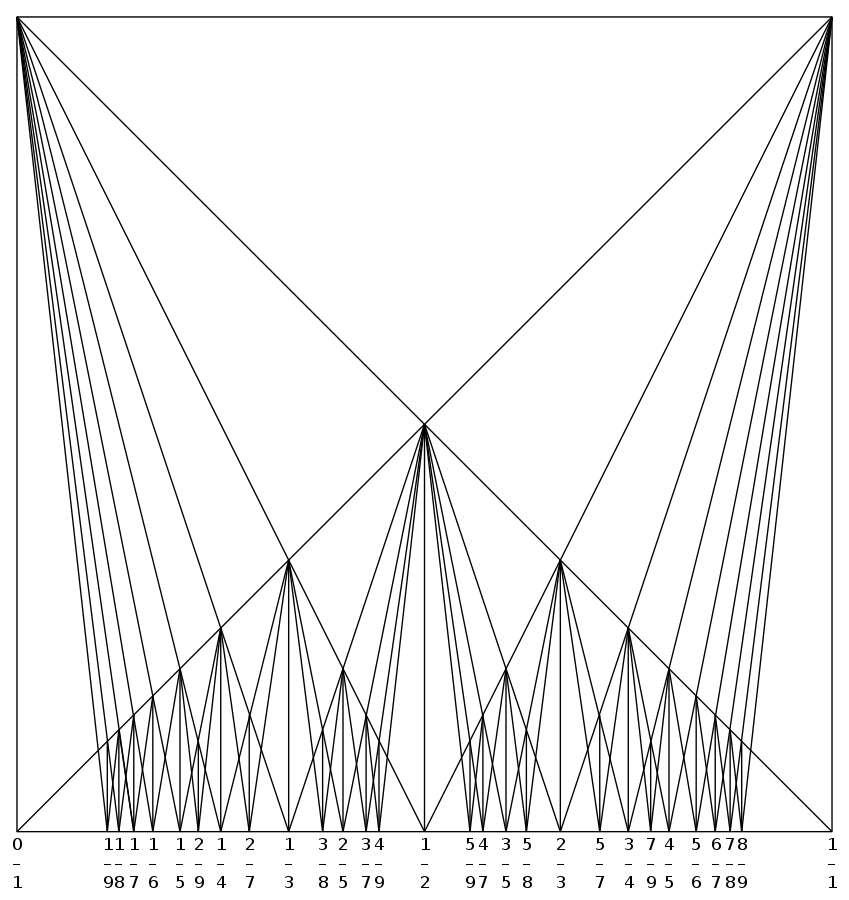
В левой половине этого дерева мы видим ровно те же дроби, что и на спектрограммах. Это не удивительно, поскольку структура резонансов в точности соответствует внутренней структуре множества рациональных чисел, которую отражает диаграмма Фарея. Об этом мы говорили в прошлой части. Вокруг резонансов на спектрограмме мы наблюдаем вторичную структуру: ярко выраженный пик резонанса, окружённый высокочастотными пиками инвариантных торов.

Что же происходит в хаотическом море? В размазанном шумном спектре выделяются тёмные полосы тех резонансов, которые породили этот странный аттрактор через разрушение гомоклинических орбит. Хаотическая орбита, блуждая по фазовому пространству, то и дело приближается к неподвижным точкам разного порядка и на какое-то время попадает в их ритм. Однако в прошлой статье мы заключили, что хаотическая орбита "забывает" о своём прошлом за ляпуновское время, которое в нашей системе составляет всего 5-10 шагов. Это значит, что в спектре странного аттрактора пиков с периодами больше 10 мы наблюдать уже не должны, поскольку настолько надолго задержаться в малой окрестности неподвижной точки хаотическая орбита не сможет.

В спектре странного аттрактора есть и низкие частоты, и высокие. Первые появляются за счёт флуктуаций и перемешивания фазового пространства, а вторые — за счёт экспоненциального разбегания соседних точек. Сплошной спектр говорит о стохастичности аттрактора, который делает примерно равновероятным кратковременное наблюдение орбиты любого периода. Это отлично демонстрирует упоминавшийся несколько раз результат Смэйла, который показал, что странный аттрактор, рождённый разрушением гетероклинических многообразий, содержит бесконечное множество неподвижных точек самого разного порядка. Кроме того, каскад удвоения периода тоже приводит к появлению бесконечного набора частот в системе.

Размерность орбит

Что ещё отличает странный аттрактор от инвариантного тора или цепочки неподвижных точек? Они по-разному выглядят внешне. Хаотическая орбита формирует "туман", заполняющий некоторую площадь фазового пространства, тогда как инвариантный тор в сечении Пуанкаре образует замкнутую линию или множество овалов, а неподвижные точки (циклы) — дискретное конечное множество точек. С формальной точки зрения, эти орбиты, как топологические объекты, отличаются размерностью. 

Эту характеристику можно определить различными способами, которые зависят от задачи. Для характеризации дискретных множеств точек чаще всего используется размерность Хаусдорфа или приближающаяся к ней корреляционная размерность. Именно последнюю мы и рассмотрим подробнее, поскольку она легко вычисляется и позволяет оценить не только размерность объекта, но целый спектр размерностей для различных масштабов в метризованном фазовом пространстве. 

Что отличает одномерную линию от дискретного множества нульмерных точек? В первую очередь непрерывность. Однако если точек будет много, из них можно сформировать дискретные фигуры, которые будут в большей степени подобны нульмерному, одномерному или двумерному объекту, как показано на рисунке. 

Отличает их распределение количества точек по расстояниям между ними, а точнее, то, как зависит количество точек, попадающих в диск, от его радиуса. Получить оценку этого распределения можно следующим очень простым образом. Для множества из n точек находим расстояния между всеми точками (если точек много, то между некоторой случайной выборкой, образующей подмножество точек). Упорядоченное множество расстояний определяет функцию , где — количество пар точек, оказавшихся на расстоянии, меньше друг от друга. Нормировав эту функцию количеством пар: , мы получаем наблюдаемое распределение вероятности для всего диапазона расстояний. Диапазон расстояний и количество пар очень велики, так что мы воспользуемся логарифмической шкалой, позволяющий соотносить между собой величины разных порядков. 

Давайте посмотрим как выглядит такое распределение для некоторых множеств из 500 точек: нескольких очень плотных кластеров, одномерной линии, случайно заполненного точками квадрата и множества Серпинского. 

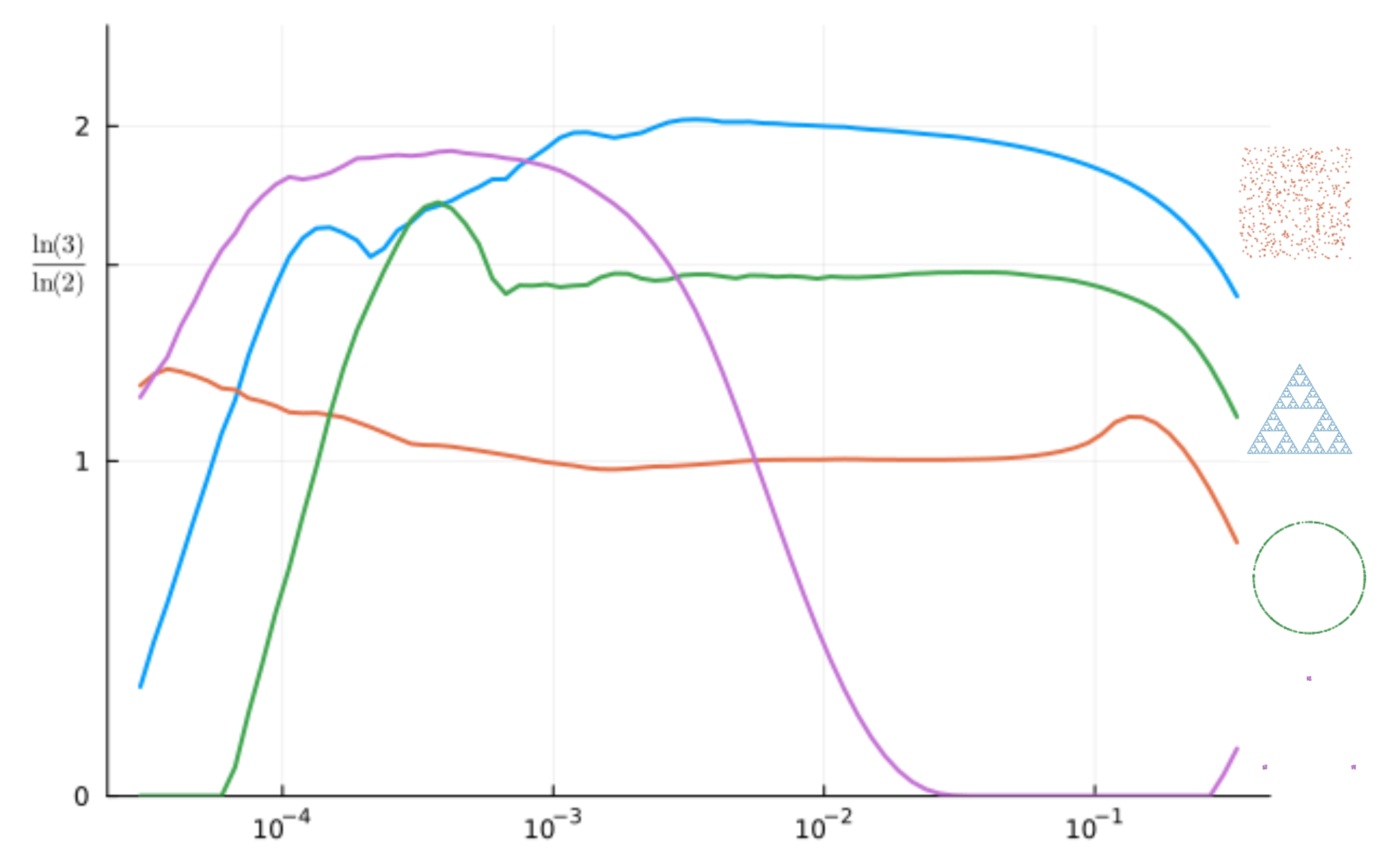
братите внимание на отчëтливые линейные участки на графиках распределения. Линейным графикам в логарифмических координатах соответствует степенная зависимость, а наклон линии показывает еë степень. Этот значит, что на некоторых масштабах количество точек, попадающих в диск зависит от радиуса диска так:

Этот показатель называется корреляционной размерностью множества точек в некотором диапазоне расстояний и даëт оценку для размерности Хаусдорфа, которая вычисляется более сложным образом. 

Из наших примеров видно, что точки, лежащие на окружности, ожидаемо имеет размерность, близкую к единице, однако, на малых масштабах его размерность падает до нуля. Регулярная решётка и заполненный случайным образом диск имеют размерность, близкую к двум, а треугольник Серпинского обладает дробной размерностью . Множества с дробной размерностью называются фрактальными. Они могут быть самоподобными, как множество Серпинского, или нет, это не важно. 

Обратите внимание на то, что множество точек, образующих несколько компактных кластеров, имеет на малых масштабах размерность, близкую к двум, однако в масштабах расстояний между кластерами, размерность падает, показывая, что сами кластеры двумерны, но они образуют дискретное множество нулевой размерности.

Можно построить график усреднëнных наклонов зависимости в логарифмических координатах, и получить спектр размерностей множества точек. Примеры таких спектров для описанных выше множеств показаны на рисунке:

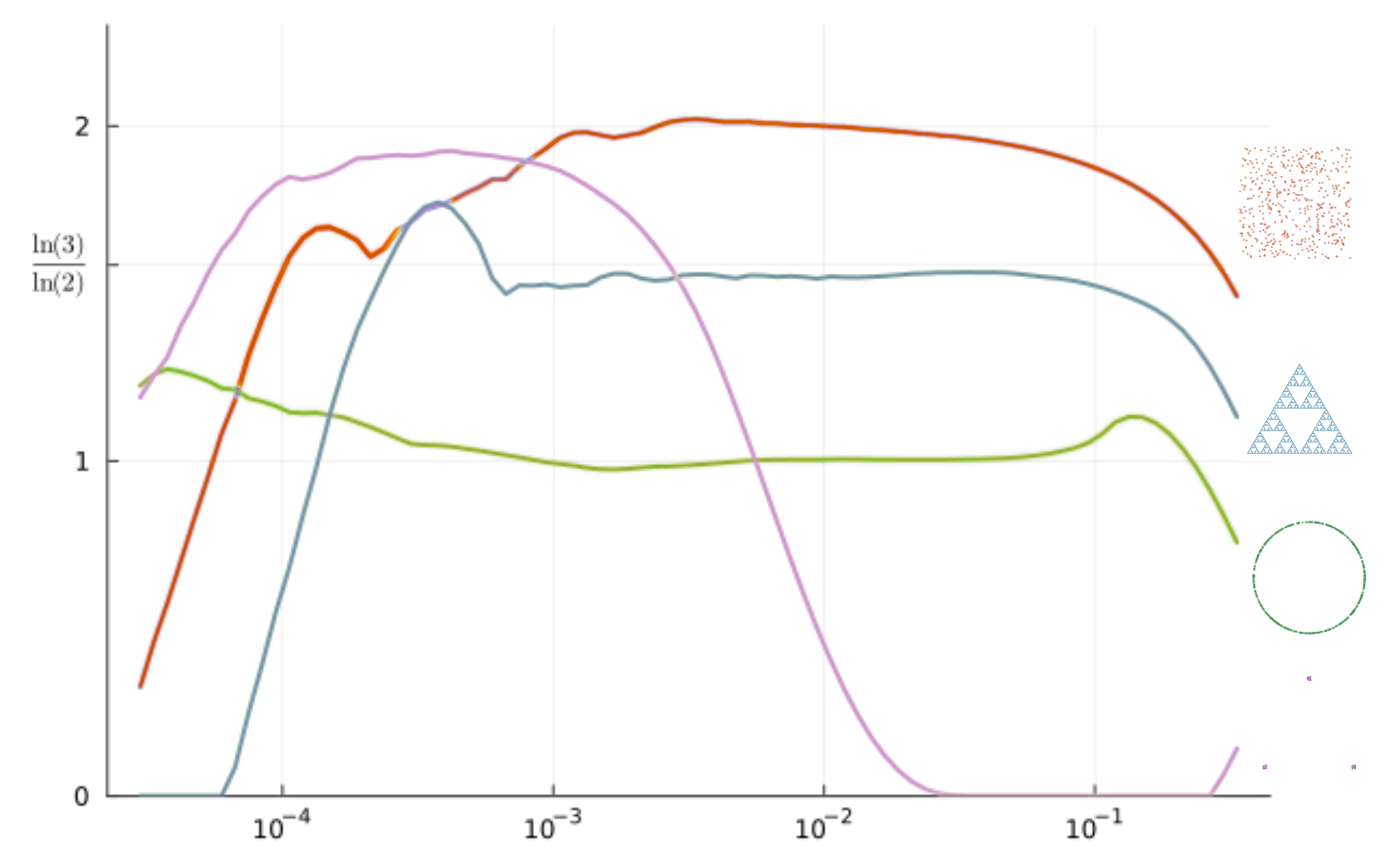
Вернëмся к нашей системе. Спектры корреляционной размерности, позволят нам получить более подробную количественную топологическую картину инвариантных многообразий еë сечения Пуанкаре . 

Надо сказать, корреляционная размерность не самая информативная характеристика гамильтоновых систем. В отличие от дисспативных систем, гамильтоновы странные аттракторы по мере накопления точек не выявляют какой‑то фрактальной структуры, и равномерно заполняют фазовое простраснтво, демонстрируя одно ключевое их свойство — эргодичность.

Для диагностики странного аттрактора размерность годится, но показатели Ляпунова и частотные спектры дают больше информации. Впрочем, мы можем построить симпатичные спектры размерностей для семейств орбит системы при фиксированной энергии.