В одном из совместных исследований нам с Хайди требовалось решить такую задачу. Допустим, нам требуется синхронизировать между двумя узлами хеш-граф, например, как в репозитории Git. В Git каждый коммит идентифицируется через соответствующий ему хеш, причём, в коммит могут включаться хеши коммитов-предшественников (то есть, конкретный коммит может содержать более одного хеша, если он получен слиянием). Мы хотели получить минимальное множество таких коммитов, которыми должны обменяться два узла, чтобы их графы получились одинаковыми.
Вы могли бы спросить: «а разве эта задача ещё не решена»? Git приходится выполнять такую операцию всякий раз, когда вы направляете ему команду
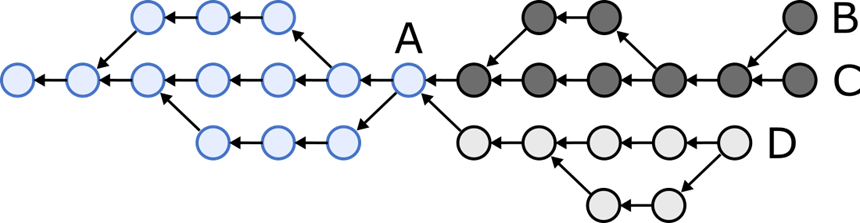
Например, имеем два узла, и первому соответствует один из следующих хеш-графов, а второму – другой (здесь кружочки соответствуют коммитам, а стрелки ставятся там, где один коммит ссылается на хеш другого). Голубая часть графа (коммит А) и узлы, расположенные левее него совместно используется обоими графами, тогда как тёмно-серая и светло-серая части обе существуют в одном экземпляре, каждая – в своём графе.
Мы хотим согласовать состояния двух узлов так, чтобы один узел отправлял все коммиты, окрашенные тёмно-серым, другой – коммиты, окрашенные светло-серым, и на выходе у нас получался бы следующий граф:
Как выработать путь, который позволял бы эффективно определять, какие коммиты два узла должны пересылать друг другу?
Сначала давайте определимся с терминологией. Мы говорим, что коммит A предшествует коммиту B, если B ссылается на хеш A, либо если имеется цепочка ссылок, ведущая от B к A. Если A – это предшественник B, то B следует за A. Наконец, определяем головы графа – это такие коммиты, за которыми ни один коммит не следует. В вышеприведённом примере «головами» являются узлы B, C и D. (Это определение немного отличается от смысла, который вкладывается в HEAD в системе Git.)
Алгоритм согласования прост, если ситуация предполагает быструю «перемотку вперёд»: если головы одного узла – это коммиты, которые уже есть на другом узле. В данном случае один узел посылает другому хеши своих голов, а другой отсылает в ответ все коммиты, являющиеся «наследниками» голов первого узла. Но в вышеприведённом примере ситуация ещё более хитрая: головы B и C одного узла не известны второму узлу, и точно так же голова D не известна первому узлу.
Чтобы согласовать два графа, необходимо выявить, какие коммиты являются последними общими предками голов обоих графов (на графе они обозначены через А). После этого узлы могут отсылать друг другу все коммиты, являющиеся потомками общих предков.
В качестве первой попытки попробуем вот что: два узла отсылают друг другу свои головы; если в них содержатся хеши неизвестных предков, то они запрашиваются, и так продолжается до тех пор, пока все хеши не станут разрешаться в известные коммиты. Следовательно, узлы постепенно прокладывают путь от голов к общим предкам. Такой подход работает, но работает медленно, если ваш граф содержит длинную цепочку коммитов, поскольку количество необходимых в данном случае обратных проходов равняется длине самого долгого пути от головы до общего предка.
«Умный» протокол передачи данных, используемый в Git, в сущности, работает именно так, с той оговоркой, что он отправляет 32 хеша за один раз, сокращая таким образом количество обратных ходок. Почему 32? Кто знает… это компромисс. Посылаем сразу большую партию хешей, поэтому количество операций уменьшается, но каждый запрос и отклик получается крупнее. Можно предположить, что разработчики остановились на числе 32, так как такое количество позволяло сохранить приемлемое соотношение между задержкой и шириной полосы.
В свежих версиях Git также поддерживается экспериментальный алгоритм «пропуска», который активируется конфигурационной опцией fetch.negotiationAlgorithm. Этот алгоритм позволяет не продвигаться на фиксированное число предшественников на каждом ходу, а пропускать некоторые коммиты и таким образом быстрее добираться до общих предков. Размер пропускаемого участка постепенно возрастает при каждом следующем проходе в соответствии с последовательностью чисел Фибоначчи – то есть, растёт по экспоненте. Так количество проходов сокращается по принципу O (log n), но в итоге можно проскочить мимо некоторых общих предков, и из-за этого протокол может зря пересылать некоторые из тех коммитов, что уже есть на другом узле.
В научной статье, которая выложена на сайте arXiv, мы с Хайди предлагаем новый алгоритм, позволяющий проводить согласование такого рода. Он довольно прост, если вы уже знаете, как работают фильтры Блума.
Каждый узел не только отправляет хеши своих голов, но и конструирует фильтр Блума, в котором содержатся хеши известных ему коммитов. В нашем прототипе мы выделяем по 10 бит (1,25 байт) на коммит. Это число можно скорректировать, но обратите внимание: так получается гораздо компактнее, чем если отправлять полный 16-байтовый хеш (в случае с SHA-1, используемым в Git) или 32-байтный хеш (для SHA-256, отличающимся повышенной безопасностью) для каждого коммита. Более того, мы отслеживаем количество голов начиная с последнего момента, в который мы согласовали состояние системы с конкретным узлом. После этого фильтру Блума требуется только включить те коммиты, что были добавлены после последнего согласования.
Получив такой фильтр Блума, узел проверяет хеши собственных коммитов, уточняя, присутствуют ли они в фильтре. Любые коммиты, чьих хешей нет в фильтре Блума, а также их наследники, сразу же можно отправлять на другой узел, поскольку мы можем быть уверены, что на другом узле об этих коммитах ничего не известно. Что касается любых коммитов, чьи хеши присутствуют в фильтре Блума, можно предположить, что другому узлу, вероятно, известно об этих коммитах. Но это не точно, поскольку возможны ложноположительные результаты.
Получив все коммиты, которые не фигурировали в фильтре Блума, проверяем, знаем ли мы хеши всех предшественников. Если каких-то не хватает, то мы запрашиваем их, совершая для этого дополнительный проход, при этом используем тот же самый алгоритм обхода графа, что и ранее. Учитывая, как при этом формируется вероятность ложноположительных результатов, по мере роста n экспоненциально снижается вероятность того, что нам потребуется n раз сходить туда и обратно/ Например, может существовать 1%-я вероятность, что вам потребуется обернуться один раз, вероятность 0,0001% что потребуется обернуться четыре раза и так далее. Почти все согласования завершаются за один круг.
Наш алгоритм, в отличие от того алгоритма пропуска коммитов, что используется в Git, никогда без надобности не посылает каких-либо коммитов, которые уже есть на другой стороне, а фильтры Блума очень компактны, даже при работе с длинной историей коммитов.
В нашей статье также доказано, что этот алгоритм позволяет узлам взаимно синхронизировать состояние даже при наличии произвольного количества вредоносных узлов, благодаря чему становится невосприимчив к атакам Сивиллы. Далее мы доказываем теорему, демонстрирующую, приложения какого типа можно и нельзя реализовать в таком «Сивилло-неуязвимом» ключе, не требуя при этом каких-либо анти-Сивилльных контрмер, например, доказательства работоспособности или централизованного управления эксклюзивными блокчейнами.
Всё это напрямую важно при применении в исходно-локальных пиринговых приложениях, где требуется синхронизировать состояние множества приложений, работающих на разных устройствах, но при этом приложения не обязательно должны доверять друг другу или полагаться при работе на доверенные сервера. Полагаю, наш алгоритм также пригодится при работе с блокчейнами, использующими графы хешей, но не слишком много о них знаю. Итак, синхронизация истории коммитов в Git – всего лишь один из многих возможных практических контекстов. Здесь я привожу в качестве примера именно его, так как большинство разработчиков хотя бы примерно знает, как работает этот механизм.
Подробности об алгоритме и теоремах изложены в статье, так что не буду повторять их здесь. Только кратко опишу некоторые интересные вещи, рассказ о которых не попал в статью.
Возможно, у вас возникает вопрос: а что, если не создавать фильтр Блума, в котором выделяется 10 бит на коммит, а просто усекать хеши коммитов до 10 бит и отправлять их в таком виде? Тогда мы занимали бы всё ту же долю сетевой полосы, и интуитивно кажется, будто эти варианты эквивалентны.
На самом деле – нет. Фильтры Блума работают гораздо лучше усечённых хешей. Сейчас объясню, почему, добавив немного материала из теории вероятности.
Допустим, у нас есть хеш-граф, в котором содержится n разных элементов, и мы хотим использовать b бит на элемент (так что общий размер структуры данных составит m=bn бит). При использовании усечённых хешей у нас будет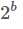
возможных значений на каждый b — битный хеш. Следовательно, имея два произвольно выбранных равномерно распределённых хеша, получаем следующую вероятность, что они окажутся одинаковыми: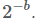 
Если у нас n равномерно распределённых хешей, то вероятность, что все они разные, начиная от заданного b-разрядного хеша, равна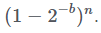
Следовательно, вероятность ложноположительного результата, что заданный b-разрядный хеш равен одному или более n хешей:
P(ложноположительный результат в усечённых хешах)=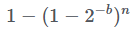
С другой стороны, работая с фильтром Блума, в исходной позиции мы имеем все m битов установленными в ноль, а затем для каждого элемента мы устанавливаем k бит в единицу. После одной равномерно распределённой операции установки разрядов, имеем следующую вероятность, что заданный бит будет равен нулю: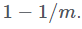
. Следовательно, после kn операций установки разрядов, заданный бит всё равно будет равен нулю с вероятностью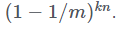 
Фильтр Блума даёт ложноположительный результат, когда мы проверяем k разрядов для некоторого элемента, и все они равны единице, хотя этого элемента даже нет в наборе. Вероятность, что такое произойдёт, равна
P(ложноположительные результаты в фильтре Блума)=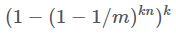
Из этих выражений не очевидно, какой из двух вариантов лучше, так что я построил графики вероятностей ложноположительных результатов при работе с усечёнными хешами и фильтрами Блума для переменного количества элементов n и с параметрами b=10, k=7, m=bn:
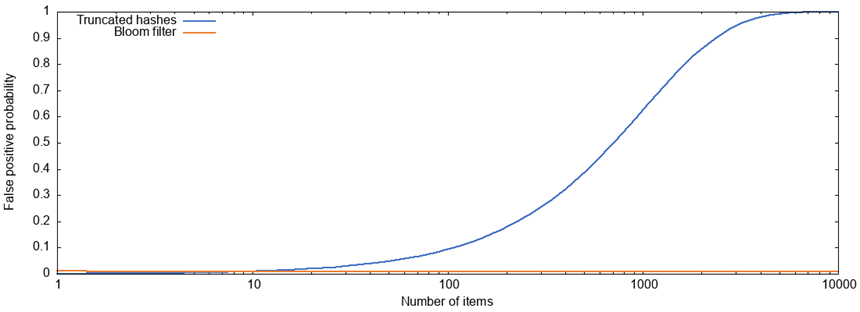
При работе с фильтром Блума, пока мы увеличиваем размер фильтра пропорционально количеству элементов (здесь у нас по 10 бит на элемент) вероятность ложноположительного результата остаётся практически постоянной и держится на уровне около 0,8%. Но при работе с усечёнными хешами тех же размеров ситуация гораздо хуже. При охвате более 1 000 элементов вероятность ложноположительного результата превышает 50%.
Вот почему так происходит: при работе с 10-разрядными усечёнными хешами у нас всего 1 024 возможных значений хеша. Будь у нас 1000 разных элементов, большинство из этих 1 024 возможных значений были бы уже выбраны. Если бы мы, работая с усечёнными хешами, хотели бы держать вероятность ложноположительного результата постоянной, то потребовалось бы использовать тем больше разрядов на элемент, чем больше элементов в наборе. Поэтому в пересчёте на количество элементов размер структуры данных рос бы быстрее, чем линейно.
Рассматривая проблему в таком ракурсе, вполне понятно, почему фильтры Блума работают так хорошо, обходясь постоянным количеством разрядов на элемент!
Приведённая выше формула расчёта количества ложноположительных результатов при работе с фильтрами Блума приводится часто, но вообще не совсем верна. Если быть точным, она даёт нижнюю границу истинной вероятности ложноположительного результата (подробнее – в этой статье).
Просто из любопытства я написал небольшой скрипт на Python, высчитывающий вероятность ложноположительного результата для усечённых хешей и фильтров Блума именно по точной формуле. К счастью, при интересующих нас значениях параметров разница между приблизительной и точной вероятностью очень невелика. Здесь также содержится скрипт Gnuplot, при помощи которого строится вышеприведённый график.
Питер предположил, что кукушкин фильтр в данном случае мог бы сработать ещё лучше, чем фильтр Блума, но я такую возможность пока не рассматривал. Честно говоря, подход с фильтром Блума уже настолько отлажен и так прост, что я не уверен, стоит ли мириться с той дополнительной сложностью, которая была бы привнесена с более изощрённой структурой данных.
Вот и всё на сегодня. Наша статья лежит здесь: arxiv.org/abs/2012.00472.
Статья продолжает темы, ранее разобранные автором в книге "Высоконагруженные приложения. Программирование, масштабирование, поддержка". Скидка 40% по купону — Клеппман
Вы могли бы спросить: «а разве эта задача ещё не решена»? Git приходится выполнять такую операцию всякий раз, когда вы направляете ему команду
git pull или git push! Да, так и есть, и некоторые случаи довольно просты, но другие гораздо сложнее. Более того, тот алгоритм, что используется в Git, не слишком хорошо документирован – в общем, мы полагали, что у нас может получиться лучше.Например, имеем два узла, и первому соответствует один из следующих хеш-графов, а второму – другой (здесь кружочки соответствуют коммитам, а стрелки ставятся там, где один коммит ссылается на хеш другого). Голубая часть графа (коммит А) и узлы, расположенные левее него совместно используется обоими графами, тогда как тёмно-серая и светло-серая части обе существуют в одном экземпляре, каждая – в своём графе.
Мы хотим согласовать состояния двух узлов так, чтобы один узел отправлял все коммиты, окрашенные тёмно-серым, другой – коммиты, окрашенные светло-серым, и на выходе у нас получался бы следующий граф:
Как выработать путь, который позволял бы эффективно определять, какие коммиты два узла должны пересылать друг другу?
Обход графа
Сначала давайте определимся с терминологией. Мы говорим, что коммит A предшествует коммиту B, если B ссылается на хеш A, либо если имеется цепочка ссылок, ведущая от B к A. Если A – это предшественник B, то B следует за A. Наконец, определяем головы графа – это такие коммиты, за которыми ни один коммит не следует. В вышеприведённом примере «головами» являются узлы B, C и D. (Это определение немного отличается от смысла, который вкладывается в HEAD в системе Git.)
Алгоритм согласования прост, если ситуация предполагает быструю «перемотку вперёд»: если головы одного узла – это коммиты, которые уже есть на другом узле. В данном случае один узел посылает другому хеши своих голов, а другой отсылает в ответ все коммиты, являющиеся «наследниками» голов первого узла. Но в вышеприведённом примере ситуация ещё более хитрая: головы B и C одного узла не известны второму узлу, и точно так же голова D не известна первому узлу.
Чтобы согласовать два графа, необходимо выявить, какие коммиты являются последними общими предками голов обоих графов (на графе они обозначены через А). После этого узлы могут отсылать друг другу все коммиты, являющиеся потомками общих предков.
В качестве первой попытки попробуем вот что: два узла отсылают друг другу свои головы; если в них содержатся хеши неизвестных предков, то они запрашиваются, и так продолжается до тех пор, пока все хеши не станут разрешаться в известные коммиты. Следовательно, узлы постепенно прокладывают путь от голов к общим предкам. Такой подход работает, но работает медленно, если ваш граф содержит длинную цепочку коммитов, поскольку количество необходимых в данном случае обратных проходов равняется длине самого долгого пути от головы до общего предка.
«Умный» протокол передачи данных, используемый в Git, в сущности, работает именно так, с той оговоркой, что он отправляет 32 хеша за один раз, сокращая таким образом количество обратных ходок. Почему 32? Кто знает… это компромисс. Посылаем сразу большую партию хешей, поэтому количество операций уменьшается, но каждый запрос и отклик получается крупнее. Можно предположить, что разработчики остановились на числе 32, так как такое количество позволяло сохранить приемлемое соотношение между задержкой и шириной полосы.
В свежих версиях Git также поддерживается экспериментальный алгоритм «пропуска», который активируется конфигурационной опцией fetch.negotiationAlgorithm. Этот алгоритм позволяет не продвигаться на фиксированное число предшественников на каждом ходу, а пропускать некоторые коммиты и таким образом быстрее добираться до общих предков. Размер пропускаемого участка постепенно возрастает при каждом следующем проходе в соответствии с последовательностью чисел Фибоначчи – то есть, растёт по экспоненте. Так количество проходов сокращается по принципу O (log n), но в итоге можно проскочить мимо некоторых общих предков, и из-за этого протокол может зря пересылать некоторые из тех коммитов, что уже есть на другом узле.
Фильтры Блума в помощь
В научной статье, которая выложена на сайте arXiv, мы с Хайди предлагаем новый алгоритм, позволяющий проводить согласование такого рода. Он довольно прост, если вы уже знаете, как работают фильтры Блума.
Каждый узел не только отправляет хеши своих голов, но и конструирует фильтр Блума, в котором содержатся хеши известных ему коммитов. В нашем прототипе мы выделяем по 10 бит (1,25 байт) на коммит. Это число можно скорректировать, но обратите внимание: так получается гораздо компактнее, чем если отправлять полный 16-байтовый хеш (в случае с SHA-1, используемым в Git) или 32-байтный хеш (для SHA-256, отличающимся повышенной безопасностью) для каждого коммита. Более того, мы отслеживаем количество голов начиная с последнего момента, в который мы согласовали состояние системы с конкретным узлом. После этого фильтру Блума требуется только включить те коммиты, что были добавлены после последнего согласования.
Получив такой фильтр Блума, узел проверяет хеши собственных коммитов, уточняя, присутствуют ли они в фильтре. Любые коммиты, чьих хешей нет в фильтре Блума, а также их наследники, сразу же можно отправлять на другой узел, поскольку мы можем быть уверены, что на другом узле об этих коммитах ничего не известно. Что касается любых коммитов, чьи хеши присутствуют в фильтре Блума, можно предположить, что другому узлу, вероятно, известно об этих коммитах. Но это не точно, поскольку возможны ложноположительные результаты.
Получив все коммиты, которые не фигурировали в фильтре Блума, проверяем, знаем ли мы хеши всех предшественников. Если каких-то не хватает, то мы запрашиваем их, совершая для этого дополнительный проход, при этом используем тот же самый алгоритм обхода графа, что и ранее. Учитывая, как при этом формируется вероятность ложноположительных результатов, по мере роста n экспоненциально снижается вероятность того, что нам потребуется n раз сходить туда и обратно/ Например, может существовать 1%-я вероятность, что вам потребуется обернуться один раз, вероятность 0,0001% что потребуется обернуться четыре раза и так далее. Почти все согласования завершаются за один круг.
Наш алгоритм, в отличие от того алгоритма пропуска коммитов, что используется в Git, никогда без надобности не посылает каких-либо коммитов, которые уже есть на другой стороне, а фильтры Блума очень компактны, даже при работе с длинной историей коммитов.
Практическая значимость
В нашей статье также доказано, что этот алгоритм позволяет узлам взаимно синхронизировать состояние даже при наличии произвольного количества вредоносных узлов, благодаря чему становится невосприимчив к атакам Сивиллы. Далее мы доказываем теорему, демонстрирующую, приложения какого типа можно и нельзя реализовать в таком «Сивилло-неуязвимом» ключе, не требуя при этом каких-либо анти-Сивилльных контрмер, например, доказательства работоспособности или централизованного управления эксклюзивными блокчейнами.
Всё это напрямую важно при применении в исходно-локальных пиринговых приложениях, где требуется синхронизировать состояние множества приложений, работающих на разных устройствах, но при этом приложения не обязательно должны доверять друг другу или полагаться при работе на доверенные сервера. Полагаю, наш алгоритм также пригодится при работе с блокчейнами, использующими графы хешей, но не слишком много о них знаю. Итак, синхронизация истории коммитов в Git – всего лишь один из многих возможных практических контекстов. Здесь я привожу в качестве примера именно его, так как большинство разработчиков хотя бы примерно знает, как работает этот механизм.
Подробности об алгоритме и теоремах изложены в статье, так что не буду повторять их здесь. Только кратко опишу некоторые интересные вещи, рассказ о которых не попал в статью.
Почему мы работаем с фильтрами Блума?
Возможно, у вас возникает вопрос: а что, если не создавать фильтр Блума, в котором выделяется 10 бит на коммит, а просто усекать хеши коммитов до 10 бит и отправлять их в таком виде? Тогда мы занимали бы всё ту же долю сетевой полосы, и интуитивно кажется, будто эти варианты эквивалентны.
На самом деле – нет. Фильтры Блума работают гораздо лучше усечённых хешей. Сейчас объясню, почему, добавив немного материала из теории вероятности.
Допустим, у нас есть хеш-граф, в котором содержится n разных элементов, и мы хотим использовать b бит на элемент (так что общий размер структуры данных составит m=bn бит). При использовании усечённых хешей у нас будет
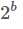возможных значений на каждый b — битный хеш. Следовательно, имея два произвольно выбранных равномерно распределённых хеша, получаем следующую вероятность, что они окажутся одинаковыми: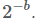 Если у нас n равномерно распределённых хешей, то вероятность, что все они разные, начиная от заданного b-разрядного хеша, равна
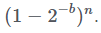Следовательно, вероятность ложноположительного результата, что заданный b-разрядный хеш равен одному или более n хешей:P(ложноположительный результат в усечённых хешах)=
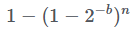
С другой стороны, работая с фильтром Блума, в исходной позиции мы имеем все m битов установленными в ноль, а затем для каждого элемента мы устанавливаем k бит в единицу. После одной равномерно распределённой операции установки разрядов, имеем следующую вероятность, что заданный бит будет равен нулю:
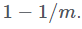. Следовательно, после kn операций установки разрядов, заданный бит всё равно будет равен нулю с вероятностью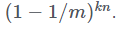 Фильтр Блума даёт ложноположительный результат, когда мы проверяем k разрядов для некоторого элемента, и все они равны единице, хотя этого элемента даже нет в наборе. Вероятность, что такое произойдёт, равна
P(ложноположительные результаты в фильтре Блума)=
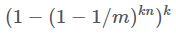
Из этих выражений не очевидно, какой из двух вариантов лучше, так что я построил графики вероятностей ложноположительных результатов при работе с усечёнными хешами и фильтрами Блума для переменного количества элементов n и с параметрами b=10, k=7, m=bn:
При работе с фильтром Блума, пока мы увеличиваем размер фильтра пропорционально количеству элементов (здесь у нас по 10 бит на элемент) вероятность ложноположительного результата остаётся практически постоянной и держится на уровне около 0,8%. Но при работе с усечёнными хешами тех же размеров ситуация гораздо хуже. При охвате более 1 000 элементов вероятность ложноположительного результата превышает 50%.
Вот почему так происходит: при работе с 10-разрядными усечёнными хешами у нас всего 1 024 возможных значений хеша. Будь у нас 1000 разных элементов, большинство из этих 1 024 возможных значений были бы уже выбраны. Если бы мы, работая с усечёнными хешами, хотели бы держать вероятность ложноположительного результата постоянной, то потребовалось бы использовать тем больше разрядов на элемент, чем больше элементов в наборе. Поэтому в пересчёте на количество элементов размер структуры данных рос бы быстрее, чем линейно.
Рассматривая проблему в таком ракурсе, вполне понятно, почему фильтры Блума работают так хорошо, обходясь постоянным количеством разрядов на элемент!
Другие подробности
Приведённая выше формула расчёта количества ложноположительных результатов при работе с фильтрами Блума приводится часто, но вообще не совсем верна. Если быть точным, она даёт нижнюю границу истинной вероятности ложноположительного результата (подробнее – в этой статье).
Просто из любопытства я написал небольшой скрипт на Python, высчитывающий вероятность ложноположительного результата для усечённых хешей и фильтров Блума именно по точной формуле. К счастью, при интересующих нас значениях параметров разница между приблизительной и точной вероятностью очень невелика. Здесь также содержится скрипт Gnuplot, при помощи которого строится вышеприведённый график.
Питер предположил, что кукушкин фильтр в данном случае мог бы сработать ещё лучше, чем фильтр Блума, но я такую возможность пока не рассматривал. Честно говоря, подход с фильтром Блума уже настолько отлажен и так прост, что я не уверен, стоит ли мириться с той дополнительной сложностью, которая была бы привнесена с более изощрённой структурой данных.
Вот и всё на сегодня. Наша статья лежит здесь: arxiv.org/abs/2012.00472.
Статья продолжает темы, ранее разобранные автором в книге "Высоконагруженные приложения. Программирование, масштабирование, поддержка". Скидка 40% по купону — Клеппман