После того как при помощи TSQL была успешна решена «Балда» (статья) я решил попробовать решить на нем «Судоку» (спасибо за идею shavluk).
Решение судоку получилось на удивление достаточно простым.
Базовая схема имеет следующий вид:
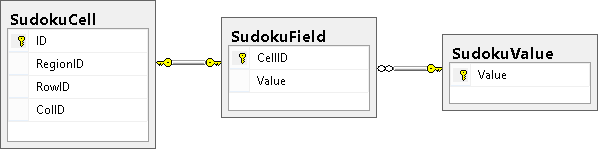
Описание таблиц:
Скрипт для создания таблиц:
Заполнение поля известными цифрами производим следующим образом:
Идентификатор ячейки (CellID) построен следующим образом:
Начальные варианты заполнения я брал со следующего сайта – ссылка.
Посмотрим, как выглядит поле:
Дальше идет алгоритм поиска решения с комментариями:
Посмотрим, на найденное решение:
Другие примеры решения:

Для задания начальных значений использовались следующие скрипты:
На моем компьютере решение находится в пределах 6 секунд (в зависимости от заданных начальных значений):
Собственно, все.
Полный скрипт можно скачать по следующей ссылке – скрипт.
Надеюсь, что статья была интересна.
Удачи и спасибо за внимание!
Переписал Oracle-запрос на MS SQL:
На моем компьютере по времени выполнения MS SQL намного обогнал Oracle:
Версия Oracle — 11g Enterprise Edition Release 11.2.0.1.0 — 64bit Production
Версия MS SQL — 2014 — 12.0.2269.0 (X64) Developer Edition (64-bit)
Решение судоку получилось на удивление достаточно простым.
Базовая схема имеет следующий вид:

Описание таблиц:
- SudokuCell – описание свойств (регион, строка, столбец) всех ячеек;
- SudokuValue – допустимые значения ячейки;
- SudokuField – поле, для задания известных цифр.
Скрипт для создания таблиц:
-- удаляем таблицы если они уже есть
IF EXISTS (SELECT * FROM sysobjects WHERE name='SudokuField') DROP TABLE SudokuField;
IF EXISTS (SELECT * FROM sysobjects WHERE name='SudokuCell') DROP TABLE SudokuCell;
IF EXISTS (SELECT * FROM sysobjects WHERE name='SudokuValue') DROP TABLE SudokuValue;
----------------------------------------------
-- описание ячеек и их свойств
----------------------------------------------
CREATE TABLE SudokuCell(
ID int NOT NULL, -- ID ячейки
RegionID int NOT NULL, -- регион
RowID int NOT NULL, -- строка
ColID int NOT NULL, -- столбец
CONSTRAINT PK_SudokuCell PRIMARY KEY(ID)
)
GO
-- заполняем таблицу
INSERT SudokuCell(ID,RegionID,RowID,ColID)
SELECT
reg.ID*100+r.i*10+c.j,
reg.ID,
(reg.ID/10-1)*3+r.i,
(reg.ID-1)%10*3+c.j
FROM (VALUES (11),(12),(13),(21),(22),(23),(31),(32),(33)) reg(ID)
CROSS JOIN (VALUES(1),(2),(3)) r(i)
CROSS JOIN (VALUES(1),(2),(3)) c(j)
GO
----------------------------------------------
-- цифры 1-9 (допустимые значения)
----------------------------------------------
CREATE TABLE SudokuValue(
Value char(1) NOT NULL,
CONSTRAINT PK_SudokuValue PRIMARY KEY(Value)
)
GO
-- заполняем таблицу
INSERT SudokuValue(Value) VALUES(1),(2),(3),(4),(5),(6),(7),(8),(9)
GO
----------------------------------------------
-- поле
----------------------------------------------
CREATE TABLE SudokuField(
CellID int NOT NULL,
Value char(1) NOT NULL,
CONSTRAINT PK_SudokuField PRIMARY KEY(CellID),
CONSTRAINT FK_SudokuField_CellID FOREIGN KEY(CellID) REFERENCES SudokuCell(ID),
CONSTRAINT FK_SudokuField_Value FOREIGN KEY(Value) REFERENCES SudokuValue(Value)
)
GO
Заполнение поля известными цифрами производим следующим образом:
-- предварительная очистка поля, на тот случай если оно заполнено
TRUNCATE TABLE SudokuField
GO
-- заполнение поля известными цифрами
INSERT SudokuField(CellID,Value)VALUES
(1122,'3'),(1123,'4'),
(1211,'1'),(1212,'5'),
(1322,'8'),(1323,'9'),(1333,'3'),
(2112,'2'),(2122,'4'),(2123,'7'),(2133,'9'),
(2212,'6'),(2223,'9'),(2232,'2'),
(2311,'8'),(2333,'1'),
(3111,'1'),
(3213,'2'),(3221,'9'),
(3313,'5'),(3332,'7'),(3333,'4')
GO
Идентификатор ячейки (CellID) построен следующим образом:
- Первая и вторая цифра числа – указывают какой это регион (строка, столбец);
- Третья и четвертая цифра – номер строки и столбца в регионе.
Начальные варианты заполнения я брал со следующего сайта – ссылка.
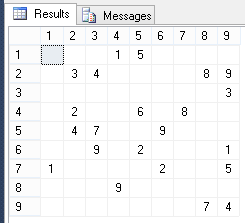
Посмотрим, как выглядит поле:
-- вид поля до заполнения
SELECT
ISNULL([1],'') [1],
ISNULL([2],'') [2],
ISNULL([3],'') [3],
ISNULL([4],'') [4],
ISNULL([5],'') [5],
ISNULL([6],'') [6],
ISNULL([7],'') [7],
ISNULL([8],'') [8],
ISNULL([9],'') [9]
FROM
(
SELECT c.RowID,c.ColID,f.Value
FROM SudokuCell c
LEFT JOIN SudokuField f ON f.CellID=c.ID
) q PIVOT(MAX(Value) FOR ColID IN([1],[2],[3],[4],[5],[6],[7],[8],[9])) p
ORDER BY RowID

Дальше идет алгоритм поиска решения с комментариями:
-- фиксируем время запуска поиска
DECLARE @StartTime datetime=SYSDATETIME();
-- получаем допустимые цифры в пустых ячейках
SELECT
-- формируем идентификатор варианта - укорачиваем его для более быстрого поиска
RIGHT(CONCAT('0',CAST(CellNo AS varchar(2)),CHAR(ASCII('a')+Value-1)),3) ID,
*
INTO #SudokuVariant
FROM
(
-- получаем все незаполненные ячейки
SELECT
ID CellID,RowID,ColID,RegionID,
-- нумеруем ячейки
CAST(DENSE_RANK()OVER(ORDER BY ID) AS int) CellNo
FROM SudokuCell
WHERE ID NOT IN(SELECT CellID FROM SudokuField)
) e
CROSS APPLY
(
-- получаем все цифры, которые могут быть вписаны в каждую пустую ячейку
SELECT v.Value
FROM SudokuCell c
JOIN SudokuField f ON f.CellID=c.ID AND (c.ColID=e.ColID OR c.RowID=e.RowID OR c.RegionID=e.RegionID)
RIGHT JOIN SudokuValue v ON v.Value=f.Value
WHERE c.ID IS NULL -- оставляем только цифры, которых нет в регионе/строке/столбце
) v
--SELECT * FROM #SudokuVariant
-- вспомогательная таблица для построения деревьев решений
CREATE TABLE #SudokuTree(
CellNo int NOT NULL,
VariantPath varchar(1000) NOT NULL
)
-- создаем корни деревьев из ячеек с CellNo=1
INSERT #SudokuTree(CellNo,VariantPath)
SELECT CellNo,ID
FROM #SudokuVariant
WHERE CellNo=1
--SELECT * FROM #SudokuTree
-- это максимальная длина цепочки
DECLARE @MaxCellNo int=(SELECT MAX(CellNo) FROM #SudokuVariant)
-- номера начальной и следующей ячеек
DECLARE @CurrCellNo int=1
DECLARE @NextCellNo int=@CurrCellNo+1
-- строим дерево
WHILE @CurrCellNo<@MaxCellNo
BEGIN
-- добавление отростков
INSERT #SudokuTree(CellNo,VariantPath)
SELECT
v.CellNo,
CONCAT(t.VariantPath,v.ID)
FROM #SudokuTree t
JOIN #SudokuVariant v ON t.CellNo=@CurrCellNo AND v.CellNo=@NextCellNo
/*
в следующий узел дерева будут входить только значения, которых нет в регионе/строке/столбце
по сути эта проверка является самодостаточной, т.к. мы уже отсекли недопустимые значения
при формировании таблицы #SudokuVariant
*/
WHERE NOT EXISTS(
SELECT *
FROM #SudokuVariant i
WHERE i.CellNo<@NextCellNo -- выше проверять нет смысла
--AND t.VariantPath LIKE '%'+i.ID+'%'
AND CHARINDEX(i.ID,t.VariantPath)>0 -- такой вариант в данном случае чуть-чуть быстрее
AND (i.RegionID=v.RegionID OR i.RowID=v.RowID OR i.ColID=v.ColID)
AND i.Value=v.Value
)
/*
т.к. полный путь у нас сохраняется в VariantPath,
то данные предыдущего уровня можно удалить
хотя по замерам, из-за дополнительной операции мы больше теряем по времени
*/
--DELETE #SudokuTree WHERE CellNo=@CurrCellNo
-- перемещаемся на уровень выше
SET @CurrCellNo+=1
SET @NextCellNo+=1
END
--SELECT * FROM #SudokuTree WHERE CellNo=@MaxCellNo
-- заполняем поле найдеными значениями
INSERT SudokuField(CellID,Value)
SELECT v.CellID,v.Value
FROM #SudokuVariant v
JOIN
(
-- если решений получилось несколько, берем самое первое
SELECT TOP 1 *
FROM #SudokuTree
WHERE CellNo=@MaxCellNo -- если промежуточные записи не удаляли
) r
ON r.VariantPath LIKE '%'+v.ID+'%'
-- удаляем временные таблицы
DROP TABLE #SudokuTree
DROP TABLE #SudokuVariant
-- выводим общее время выполнения поиска
PRINT 'Время выполнения - '+CONVERT(varchar(30),DATEADD(MS,DATEDIFF(MS,@StartTime,SYSDATETIME()),'19000101'),114);
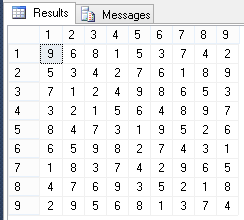
Посмотрим, на найденное решение:
-- вид поля после заполнения
SELECT
ISNULL([1],'') [1],
ISNULL([2],'') [2],
ISNULL([3],'') [3],
ISNULL([4],'') [4],
ISNULL([5],'') [5],
ISNULL([6],'') [6],
ISNULL([7],'') [7],
ISNULL([8],'') [8],
ISNULL([9],'') [9]
FROM
(
SELECT c.RowID,c.ColID,f.Value
FROM SudokuCell c
LEFT JOIN SudokuField f ON f.CellID=c.ID
) q PIVOT(MAX(Value) FOR ColID IN([1],[2],[3],[4],[5],[6],[7],[8],[9])) p
ORDER BY RowID

Другие примеры решения:

Для задания начальных значений использовались следующие скрипты:
Посмотреть скрипт...
Второй пример:
Третий пример:
-- предварительная очистка поля, на тот случай если оно заполнено
TRUNCATE TABLE SudokuField
GO
-- заполнение поля известными цифрами
INSERT SudokuField(CellID,Value)VALUES
(1112,'7'),(1113,'1'),(1131,'4'),(1132,'9'),
(1212,'9'),(1221,'3'),(1223,'6'),
(1311,'8'),(1331,'7'),(1333,'5'),
(2112,'1'),(2121,'9'),(2123,'2'),
(2211,'9'),(2233,'8'),
(2321,'6'),(2323,'3'),(2332,'2'),
(3111,'8'),(3113,'5'),(3133,'7'),
(3221,'6'),(3223,'7'),(3232,'4'),
(3312,'7'),(3313,'6'),(3331,'3'),(3332,'5')
GO
Третий пример:
-- предварительная очистка поля, на тот случай если оно заполнено
TRUNCATE TABLE SudokuField
GO
-- заполнение поля известными цифрами
INSERT SudokuField(CellID,Value)VALUES
(1132,'4'),
(1221,'9'),(1223,'4'),(1231,'8'),(1233,'5'),
(1311,'7'),(1321,'2'),(1323,'3'),
(2113,'7'),(2121,'9'),(2133,'3'),
(2212,'1'),
(2311,'6'),(2332,'5'),(2333,'2'),
(3111,'6'),(3112,'2'),(3121,'7'),
(3223,'3'),(3233,'8'),
(3323,'9')
GO
На моем компьютере решение находится в пределах 6 секунд (в зависимости от заданных начальных значений):
- Пример 1: 4.547 сек.
- Пример 2: 5.317 сек.
- Пример 3: 3.690 сек.
Собственно, все.
Полный скрипт можно скачать по следующей ссылке – скрипт.
Надеюсь, что статья была интересна.
Удачи и спасибо за внимание!
PS (04.12.2015)
Переписал Oracle-запрос на MS SQL:
WITH x AS(
SELECT
s,
CHARINDEX(' ',s) ind -- индекс первой пустой ячейки
--FROM (SELECT ' 15 34 89 3 2 6 8 47 9 9 2 11 2 5 9 74' s) q
--FROM (SELECT ' 71 9 8 3 6 49 7 5 1 9 9 2 6 3 8 2 8 5 76 6 7 7 4 35 ' s) q
FROM (SELECT ' 7 9 42 3 4 8 5 7 1 6 9 3 5262 7 3 9 8 ' s) q
UNION ALL
SELECT
CAST(STUFF(s,ind,1,z) AS varchar(81)), -- прописываем на место пустой ячейки подходящие цифры
CHARINDEX(' ',s,ind+1) -- индекс следующей пустой ячейки
FROM x
CROSS JOIN (VALUES(1),(2),(3),(4),(5),(6),(7),(8),(9)) v(z)
WHERE ind>0
AND NOT EXISTS(
SELECT *
FROM (VALUES(1),(2),(3),(4),(5),(6),(7),(8),(9)) v(lp)
WHERE z=SUBSTRING(s,(ind-1)/9*9+lp,1)
OR z=SUBSTRING(s,(ind-1)%9-8+lp*9,1)
OR z=SUBSTRING(s,((ind-1)/3)%3*3+(ind-1)/27*27+lp+(lp-1)/3*6,1)
)
)
SELECT s
FROM x
WHERE ind=0
Посмотреть Oracle-запрос...
with x( s, ind ) as
( select sud, instr( sud, ' ' )
--from ( select ' 15 34 89 3 2 6 8 47 9 9 2 11 2 5 9 74' sud from dual )
--from ( select ' 71 9 8 3 6 49 7 5 1 9 9 2 6 3 8 2 8 5 76 6 7 7 4 35 ' sud from dual )
from ( select ' 7 9 42 3 4 8 5 7 1 6 9 3 5262 7 3 9 8 ' sud from dual )
union all
select substr( s, 1, ind - 1 ) || z || substr( s, ind + 1 )
, instr( s, ' ', ind + 1 )
from x
, ( select to_char( rownum ) z
from dual
connect by rownum <= 9
) z
where ind > 0
and not exists ( select null
from ( select rownum lp
from dual
connect by rownum <= 9
)
where z = substr( s, trunc( ( ind - 1 ) / 9 ) * 9 + lp, 1 )
or z = substr( s, mod( ind - 1, 9 ) - 8 + lp * 9, 1 )
or z = substr( s, mod( trunc( ( ind - 1 ) / 3 ), 3 ) * 3
+ trunc( ( ind - 1 ) / 27 ) * 27 + lp
+ trunc( ( lp - 1 ) / 3 ) * 6
, 1 )
)
)
select s
from x
where ind = 0
На моем компьютере по времени выполнения MS SQL намного обогнал Oracle:
- Пример 1: Oracle — 1.079 сек., MS SQL — 0.303 сек.
- Пример 2: Oracle — 2.991 сек., MS SQL — 0.787 сек.
- Пример 3: Oracle — 3.037 сек., MS SQL — 0.773 сек.
Версия Oracle — 11g Enterprise Edition Release 11.2.0.1.0 — 64bit Production
Версия MS SQL — 2014 — 12.0.2269.0 (X64) Developer Edition (64-bit)
Комментарии (7)
galaxy
03.12.2015 23:36
Leran2002
04.12.2015 06:44Да, красивое и быстрое решение.
Проверил запрос для Oracle на тех же вариантах — решает в пределах 4-х секунд:
1) 1.079 сек. (мое решение — 10.930 сек.)
2) 2.991 сек. (мое решение — 12.970 сек.)
3) 3.037 сек. (мое решение — 9.047 сек.)
Oracle запрос...with x( s, ind ) as ( select sud, instr( sud, ' ' ) from ( select ' 15 34 89 3 2 6 8 47 9 9 2 11 2 5 9 74' sud from dual ) --from ( select ' 71 9 8 3 6 49 7 5 1 9 9 2 6 3 8 2 8 5 76 6 7 7 4 35 ' sud from dual ) --from ( select ' 7 9 42 3 4 8 5 7 1 6 9 3 5262 7 3 9 8 ' sud from dual ) union all select substr( s, 1, ind - 1 ) || z || substr( s, ind + 1 ) , instr( s, ' ', ind + 1 ) from x , ( select to_char( rownum ) z from dual connect by rownum <= 9 ) z where ind > 0 and not exists ( select null from ( select rownum lp from dual connect by rownum <= 9 ) where z = substr( s, trunc( ( ind - 1 ) / 9 ) * 9 + lp, 1 ) or z = substr( s, mod( ind - 1, 9 ) - 8 + lp * 9, 1 ) or z = substr( s, mod( trunc( ( ind - 1 ) / 3 ), 3 ) * 3 + trunc( ( ind - 1 ) / 27 ) * 27 + lp + trunc( ( lp - 1 ) / 3 ) * 6 , 1 ) ) ) select s from x where ind = 0


shavluk
10-15 секунд — как по мне, то долго
Вот мое решение
www.sql.ru/forum/925653/reshenie-sudoku-na-sql
Leran2002
Здесь, согласен с вами – для компьютера это очень долго.
Мое решение – решение в лоб, сделанное на скорую руку. Основная цель была получить правильный результат за приемлемое время, при этом затратив минимум своих мыслительных ресурсов – решение находится при помощи 2-х основных несложных запросов и одного цикла.
Решение получено, теперь есть куда стремиться. ))
Думаю, основные тормоза происходят из-за выражения «t.VariantPath LIKE '%'+i.ID+'%'».
Leran2002
Добавив условие:
Уменьшил время выполнения почти в 2 раза:
Leran2002
Получил еще прирост в скорости, за счет уменьшения длины идентификатора варианта:
Теперь решение находится в пределах 6 секунд:
Думаю, на этом поставлю точку.
shavluk
Проверил свое решение на ваших данных
1) 0.125 сек
2) 0.062 сек
3) 0.156 сек
Firebird 2.5