Логистика. Часть 6. Что такое нестинг? / forpes.ru

Главная
Логистика. Часть 6. Что такое нестинг?

Логистика. Часть 6. Что такое нестинг?

15.01.2024 20:39

AndreyKotlov 3 1500 Источник

Стоило только появиться первым рынкам, как торговаться на них стало уже частью процесса продаж. Считалось, что тот, кто не торгуется, получил товар или деньги нечестным путем и дел с ним лучше не иметь. Как раньше, так и в нынешнее время в большинстве случаев создание благ и зарабатывание средств даются тяжелым трудом. Оптимальная цена товара или услуги в таком контексте выступает неким синонимом справедливости.

В данной статье речь пойдет о продаже авиабилетов, но материал также может быть полезен всем, кто заинтересован в оптимальном ценообразовании.

1. Ценообразование на основе кривой спроса

Начнем с того, что ни один ресурс не может быть безграничным (в нашем случае любые товары и услуги), ведь всегда есть какие-то естественные ограничения на его количество. Спрос также не будет стремиться к бесконечности при устремлении цены к нулю. В целом, задача динамического ценообразования заключается в установлении баланса между стороной, которая создает и предлагает ресурс, и стороной, которая формирует на него запрос и потребляет его.

Простейшей и лучшей аналогией для данной задачи будут обычные весы: на одной чаше спрос, на другой предложение. Предположим, что речь идет об авиабилетах: если перевешивает спрос, то билеты очень быстро закончатся; если же перевешивает предложение, то по воздуху будет летать много пустых кресел. Необходимо равновесие, и есть всего два способа, которые позволяют его добиться.

Первый — регулирование массы грузов на чашах весов. Однако, это не всегда работает, как нам нужно: невозможно взять и уменьшить или увеличить емкость самолета на -ое количество кресел. Также нельзя убедить -ое количество пассажиров в том, что им нужно или не нужно купить билеты.

Есть и другой способ: менять положение гвоздика, вокруг которого вращается перекладина с чашами. Увеличился спрос — перемещаем точку вращения в его сторону, а если предложение стало больше спроса, перемещаем уже к нему.

Положение точки вращения перекладины весов — это и есть цена, от которой будет зависеть наличие билетов в продаже и заполняемость самолета. В то же время не стоит забывать, что ресурс является ограниченным: например, количество кресел в самолете, который выполняет регулярные рейсы Москва — Париж, чаще всего будет фиксированной величиной. По мере приближения даты вылета количество ресурса будет меняться: как правило, билеты раскупаются, но некоторые могут возвращаться обратно. Будет меняться и спрос: он обычно увеличивается по мере приближения даты вылета.

Сложность состоит в том, что количество доступного на данный момент ресурса известно, а вот каким будет спрос — нет. Предположим, что в течение недели необходимо продать 10 мест. Это значит, что нужно подобрать цену так, чтобы по окончании недели на противоположной чаше весов оказалось 10 покупателей. Спрос случаен, ведь мы не можем заглянуть в будущее и узнать, сколько будет покупок по разным ценам. При этом нам все равно необходимо найти такую цену, при которой весы не отклонились бы от точки равновесия слишком сильно.

Спрос — это главная составляющая модели ценообразования, он же представляет собой наибольшую сложность. Его простейшее определение звучит следующим образом:

Спрос — это зависимость между ценой и количеством ресурса, который покупатели могут и желают купить по строго определенной цене, в определённый промежуток времени.

Исходя из определения, выходит, что для описания спроса необходимо всего три величины:

$\mathrm{Price}$ — цена единицы ресурса (товара или услуги);
— количество ресурса (товара или услуг);
— период (промежуток) времени.

Причем описание спроса можно выразить в виде некоторой функциональной зависимости:

$Q = f(\mathrm{Price}, T).$

В дальнейшем будем называть такую модель интегральной, поскольку она показывает сумму отдельных единиц ресурса, купленных по определенной цене в период действия этой цены. Данная зависимость может содержать гораздо больше переменных, например:

время вылета самолета;
день недели;
время года;
наличие скидок и их значение;
цены конкурентов.

В то же время есть сотни других случайных факторов, которые будут влиять на спрос, такие как: погода в пункте прибытия или резкое изменение курса валют. Таким образом, спрос гораздо лучше описывается некоторой регрессионной моделью — детерминированной, но зашумленной функцией.

1.1. Детерминированная модель спроса

Очевидно, что без модели спроса никакое динамическое ценообразование невозможно в принципе. Но с чем придется столкнуться, если модель спроса уже есть? Рассмотрим простой пример: допустим, продажи на некоторый рейс позволяют определить зависимость только в двух периодах, а сами зависимости являются линейными:

$Q_{1} = [-20 \cdot \mathrm{Price} + 43]$ $Q_{2} = [-15 \cdot \mathrm{Price} + 38],$

где $\mathrm{Price} \in [1.0; 1.4]$ и изменяется с шагом 0.1, а квадратные скобки обозначают округление к ближайшему целому.

Python

import numpy as np
import pandas as pd
np.random.seed(42)
from scipy import stats
from scipy.stats import uniform, betabinom, randint, poisson, gamma
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 7, 4
rcParams['figure.dpi'] = 140
%config InlineBackend.figure_format = 'png'
import seaborn as sns
#sns.set()
#from matplotlib import cm
sns.set_style("whitegrid")

Python

f, ax = plt.subplots(1, 2, figsize=(12, 3))

price = np.round(np.arange(1, 1.5, 0.1), 1)
q1 = np.round(-20 * price + 43)
q2 = np.round(-15 * price + 38)

ax[0].plot(price, q1, 'bo-', label=r'$Q_{1}$')
ax[0].plot(price, q2, 'ro-', label=r'$Q_{2}$')
ax[0].legend()
ax[0].set_yticks(np.r_[15:25])
ax[0].set_xticks(price)
ax[0].set_xlabel('Price')
ax[0].set_ylabel('Quantity')
ax[0].set_title('Demand')

ax[1].plot(price, price * q1, 'bo-', label=r'$Q_{1}$')
ax[1].plot(price, price * q2, 'ro-', label=r'$Q_{2}$')
ax[1].legend()
ax[1].set_xlabel('Price')
ax[1].set_ylabel('Profit')
ax[1].set_xticks(price)
ax[1].set_title('Profit');

В случае продаж авиабилетов, как и многих других товаров и услуг, мы сталкиваемся с естественной дискретизацией — продавать можно только целое количество авиабилетов.

На первом графике видно, что дискретизация не всегда позволяет задавать спрос идеальной прямой линией, поэтому фраза "кривая спроса" применима даже для линейных зависимостей.

На втором графике видно, что прибыль зависит от выбираемой цены вовсе нелинейно и далеко не гладко. Значит, что даже в простейшем случае линейного спроса придется оптимизировать сумму значений нелинейных функций:

$\mathrm{Profit} = \sum_{i} f_{i}(\mathrm{Price_{i}}, T_{i}) \cdot \mathrm{Price_{i}} = \sum_{i} Q_{i} \cdot \mathrm{Price_{i}} \to \underset{\mathrm{PriceVec}}{\mathrm{max}},$

где — номер периода, $Q_{i}$ — значение спроса при цене $\mathrm{Price}_{i}$ , а $\mathrm{PriceVec}$ — вектор цен, длина которого равна .

На первый взгляд, дискретизация кажется несущественной, но на самом деле она является определяющей, поскольку из-за нее не удастся использовать градиентные методы оптимизации. Максимумы дискретных функций с учетом ограничений могут располагаться очень далеко от максимумов их непрерывных форм. Причем чем больше размерность пространства, тем больше может быть отличие. Из-за дискретизации задача приобретает скорее больше комбинаторных свойств, чем функциональных, и, как мы увидим далее, эта тенденция будет все сильнее усиливаться по мере добавления в нее новых элементов.

В конечном счете оптимизируется прибыль, т.е. сумма значений прибыли в разные периоды времени. Если предположить, что к продаже доступно всего V кресел и , то необходимо ввести всего одно простое ограничение, имеющее следующий вид:

$Q_{2} = \begin{cases}Q_{2}, & \text{ if } Q_{2} \leqslant V - Q_{1} \\V - Q_{1}, & \text{ if } Q_{2} > V - Q_{1}\end{cases}.$

Глядя на вышеприведенный график прибыли, можно подумать, что лучшими ценами будут 1.1 для первого и второго периодов, т.е. $\mathrm{PriceVec} = (1.1, 1.1)$ , но из-за введенного ограничения это не так:

Python

Q_2 = np.where(Q_1 + Q_2 > 40, 40 - Q_1, Q_2)
profit = pd.DataFrame((Q_1 * price)[:, np.newaxis] + Q_2 * price,
                      columns=price,
                      index=price)
sns.heatmap(profit, annot=True, fmt=".2f", cmap='viridis')
plt.ylabel(r'Price for $T_{1}$')
plt.xlabel(r'Price for $T_{2}$')
plt.title('Resulting profit');

График показывает, что лучшая цена билетов в первом периоде равна 1.1, а во втором — 1.3.

1.2. Добавление неопределенности

Что изменится при добавлении в модель неопределенности? Предположим, что имеющиеся кривые спроса показывают зависимость матожидания возможных объемов продаж в отдельные периоды времени, а сами значения могут испытывать случайные отклонения от их матожиданий с некоторой вероятностью. Допустим, эти отклонения подчиняются равномерному дискретному распределению. Пусть максимальные отклонения будут возможны не более чем на две единицы, т.е. если при некоторой цене ожидается значение спроса равное 19, то его максимальные и минимальные отклонения будут равны 21 и 17, а вероятности появления отдельных возможных значений [17, 18, 19, 20, 21] будут одинаковы и равны 0.2.

Казалось бы, что в дальнейшей оптимизации нет никакого смысла, ведь речь идет о матожиданиях, использование которых как раз и приведет к оптимизации средней прибыли. Однако, после добавления неопределенности целевая функция также изменится и будет иметь следующий вид:

$E(\mathrm{Profit}) = \sum_{j} \left (q^{(1)}_{j} \cdot \mathrm{Price}^{(1)} + \sum_{k} q^{(2)}_{k} \cdot \mathrm{Price}^{(2)} \cdot P(q^{(2)}_{k} | \mathrm{Price}^{(2)}) \right ) \cdot P(q^{(1)}_{j} | \mathrm{Price}^{(1)}) \to \underset{\mathrm{PriceVec}}{\mathrm{max}},$

где $q^{(1)}_{j}$ и $q^{(2)}_{k}$ — возможные отклонения спроса в первом и втором периоде, номера которых указаны в скобках в верхнем индексе. $P(q^{(1)}_{j} | \mathrm{Price}^{(1)})$ и $P(q^{(2)}_{k} | \mathrm{Price}^{(2)})$ — вероятность наблюдения отклонений $q^{(1)}_{j}$ и $q^{(2)}_{k}$ при условии, что используются цены $\mathrm{Price}^{(1)}$ и $\mathrm{Price}^{(2)}$ .

Теперь необходимо оптимизировать среднюю прибыль, но с учетом уже знакомого ограничения на количество мест:

$q^{(2)}_{k} = \begin{cases}q^{(2)}_{k}, & \text{ if } q^{(2)}_{k} \leqslant V - q^{(1)}_{j} \\V - q^{(1)}_{j}, & \text{ if } q_{j}^{(2)} > V - q^{(1)}_{j}\end{cases},$

Получится немного неожиданный результат:

Python

res_profit = []
for i in range(5):
    profit_row = []
    for j in range(5):
        Q1 = (np.c_[-2:3] + q1[i])
        Q2 = (np.r_[-2:3] + q2[j])
        Q2 = np.where(Q1 + Q2 > 40, 40 - Q1, Q2)
        profit_ij = np.sum((price[i] * Q1.flatten() + price[j] * Q2.sum(axis=1)*0.2)*0.2)
        profit_row.append(profit_ij)
    res_profit.append(profit_row)
    
res_profit = pd.DataFrame(res_profit,
                          columns=price,
                          index=price)

sns.heatmap(res_profit, annot=True, fmt=".2f", cmap='viridis')
plt.ylabel(r'Price in $T_{1}$')
plt.xlabel(r'Price in $T_{2}$')
plt.title('Resulting Average Profit');

Лучшая цена билетов во втором периоде изменилась с 1.3 на 1.4: связано это с тем, что из-за ограничения в 40 мест некоторые отклонения во втором периоде продаж просто не реализуются, поскольку округляются так, чтобы это ограничение не нарушать. Кроме того, наблюдается локальный максимум при $\mathrm{PriceVec} = (1.2, 1.2)$ , требуя глобальной оптимизации.

Поскольку выше шла речь о комбинаторном характере и глобальной оптимизации, то можно предположить, что без эвристических методов не обойтись. Так как речь также идет об оптимизации средней прибыли, это значит, что ее придется как-то оценивать. Можно немного забежать вперед и проверить, что будет, если вычислять среднюю прибыль не аналитически, а моделируя продажи, скажем, 100 раз для некоторой пары цен:

Python

def demand(price, period, high=2, low=2):
    a = [-20, -15]
    b = [43, 38]
    q = np.round(a[period] * price + b[period])
    d = randint.rvs(q - low, q + high + 1)
    return d

def profit_s(price_1, price_2):
    q1 = demand(price_1, 0)
    q2 = demand(price_2, 1)
    if q1 + q2 > 40:
        q2 = 40 - q1
    profit = q1 * price_1 + q2 * price_2
    return profit

means_profit_1 = [np.mean([profit_s(1.2, 1.2) for i in range(100)]) for j in range(100)]
sns.kdeplot(means_profit_1, label='(1.2, 1.2)')

means_profit_2 = [np.mean([profit_s(1.1, 1.4) for i in range(100)]) for j in range(100)]
sns.kdeplot(means_profit_2, label='(1.1, 1.4)')

means_profit_3 = [np.mean([profit_s(1.2, 1.4) for i in range(100)]) for j in range(100)]
sns.kdeplot(means_profit_3, label='(1.2, 1.4)')
plt.title('KDE of average profit deviations')
plt.legend(title=r'$\overrightarrow{\mathrm{Price}}$');

График показывает, что значения средней прибыли могут очень сильно отклоняться, а это значит, что вместо оптимального решения можно найти субоптимальное. Такие отклонения станут сложностью для любой эвристики, однако аналитические вычисления тоже не всегда возможны. С одной стороны, различие в 0.35% между оптимальным и субоптимальным решением может показаться несущественным, но если речь идет о больших оборотах, то лучше потратить некоторые дополнительные усилия для поиска оптимального решения.

В то же время небольшие различия в средней прибыли при разных ценах вовсе не означает, что их нет в самом процессе продаж:

Python

fig, ax = plt.subplots(2, 2, figsize=(12, 8))

def sales(ind):
    n_iter = 5000
    test_data = []
    for _ in range(n_iter):
        q1 = demand(price[ind[0]], 0)
        q2 = demand(price[ind[1]], 1)
        
        if q1 + q2 > 40:
            q2_correct = 40 - q1
            res_profit = q1 * price[ind[0]] + q2_correct * price[ind[1]]
            test_data.append([q1 + q2, res_profit, 'larger capacity'])
        if q1 + q2 == 40:
            res_profit = q1 * price[ind[0]] + q2 * price[ind[1]]
            test_data.append([q1 + q2, res_profit, 'equal to capacity'])
        if q1 + q2 < 40:
            res_profit = q1 * price[ind[0]] + q2 * price[ind[1]]
            test_data.append([q1 + q2, res_profit, 'less capacity'])
    test_data_df = pd.DataFrame(test_data, 
                      columns=['demand', 'profit', 'occupancy'])
    return test_data_df

data = sales((1, 4))

sns.histplot(data=data, 
             x=data['demand'],
             hue='occupancy',
             hue_order=['less capacity', 'equal to capacity', 'larger capacity'],
             discrete=True,
             stat='probability',
             palette='Dark2',
             ax=ax[0, 0])

ax[0, 0].set_xticks(np.r_[31:45])
ax[0, 0].set_title('Occupancy rate\nwhen using a prices vector (1.1; 1.4)')

sns.histplot(data.profit, bins=np.r_[40.01 : 52 : 1], stat='probability', ax=ax[0, 1])
ax[0, 1].axvline(data.profit.mean(), color='r')
ax[0, 1].set_title('Distribution of profit values\nwhen using a price vector (1.1; 1.4)')

data = sales((2, 4))

sns.histplot(data=data, 
             x=data['demand'],
             hue='occupancy',
             hue_order=['less capacity', 'equal to capacity', 'larger capacity'],
             discrete=True,
             stat='probability',
             palette='Dark2',
             ax=ax[1, 0])


ax[1, 0].set_xticks(np.r_[31:45])
ax[1, 0].set_title('Occupancy rate\nwhen using a prices vector (1.2; 1.4)')

sns.histplot(data.profit, bins=np.r_[40.01 : 52 : 1], stat='probability', ax=ax[1, 1])
ax[1, 1].axvline(data.profit.mean(), color='r')
ax[1, 1].set_title('Distribution of profit values\nwhen using a price vector (1.2; 1.4)')

plt.tight_layout();

Фиолетовые столбцы показывают возможное значение спроса, которое превышает количество доступных мест. Поскольку это значение все равно будет округлено до 40, оно все-таки полезно тем, что позволяет судить о том, как быстро билеты могут пропасть из продажи. Различия в этом плане очень большие и составляют порядка 10%. Большие различия наблюдаются и в распределении возможных значений прибыли, хотя их средние значения, действительно, очень близки друг к другу.

Важно отметить, что цены влияют не только на среднюю прибыль, но и на процесс продаж: например, в конкурентной борьбе вполне возможна ситуация, когда снижение цены не приведет к ощутимому снижению прибыли, но за это придется заплатить тем, что билеты, доступные к продаже, будут раньше заканчиваться.

Данный график позволяет учитывать убытки как от пустых кресел, так и от упущения потенциальных клиентов, которым не хватило кресел (потенциальная прибыль). В предыдущей статье мы учитывали их, но следует отметить, что их учет необходим, только если мы можем менять емкость самолета — заменить его на другой тип или перераспределять емкость его отдельных классов обслуживания. Сейчас мы учитываем только среднюю прибыль, но данная информация о распределении заполняемости позволяет добиться гораздо большего количества решения задач по расстановке флота и формирования расписания. Обычно эти задачи решают в детерминированной форме и используют только наиболее вероятные значения — в нашем случае мы бы взяли значение 36 или 38. В стохастической постановке же мы должны использовать все представленные на графиках распределения целиком.

1.3. Корректирующие цены и их оптимизация

Поскольку спрос может испытывать случайные отклонения, то было бы неплохо иметь план действий в случае появления того или инного значения. Например, если в первом периоде используется цена 1.2, то возможные отклонения могут быть равны любому значению из интервала [17; 21]. План действий в таком случае бы просто включал указание о том, какую цену использовать во втором периоде, если в первом периоде наблюдается значение спроса, равное 18 или 20.

Оптимизация средней прибыли в данном случае заключается в рассмотрении вероятностей всех возможных комбинаций случайных отклонений как в первом, так и во втором периоде:

$E(\mathrm{Profit}) = \sum_{j} \left ( q^{(1)}_{j} \cdot \mathrm{Price}^{(1)} + \sum_{k} q^{(2)}_{k} \cdot \mathrm{Price}^{(2)}_{j} \cdot P^{(2)}_{k}(q^{(2)}_{k} | \mathrm{Price}^{(2)}_{j}) \right ) \cdot P^{(1)}_{j}(q^{(1)}_{j} | \mathrm{Price}^{(1)}) \to \underset{(\mathrm{Price}^{(1)}, \mathrm{PriceVec}^{(2)})}{\mathrm{max}},$

где $q^{(1)}_{j}$ и $q^{(2)}_{k}$ — это возможные значения спроса в первом и втором периоде (верхний индекс, указанный в скобках, обозначает номер периода), — нумерует все возможные значения спроса в первом периоде, а индекс — нумерует все возможные значения спроса во втором периоде при условии, что установлена цена $\mathrm{Price}^{(2)}_{j}$ , соответствующая -му отклонению в первом периоде. $P^{(1)}_{j}(q^{(1)}_{j} | \mathrm{Price}^{(1)})$ и $P^{(2)}_{k}(q^{(2)}_{k} | \mathrm{Price}^{(2)}_{j})$ — это вероятности наблюдения конкретных отклонений спроса при соответствующей цене. А единственное ограничение по-прежнему связано только с тем, что количество продаваемых билетов не может превышать .

Выглядит довольно громоздко, но на деле все достаточно просто. Допустим, что мы выбрали цену $\mathrm{Price}^{(1)} = 1.2$ в первом периоде и нашли оптимальный вектор корректирующих цен $\mathrm{PriceVec}^{(2)} = (1.2, 1.2, 1.4, 1.4, 1.4)$ во втором периоде. Для их обозначения введем переменные и , содержащие индексы соответствующих цен:

Python

q1 = np.round(-20 * price + 43).astype(int)
q2 = np.round(-15 * price + 38).astype(int)

x, Y = 2, [2, 2, 4, 4, 4]

q1

Результат

array([23, 21, 19, 17, 15])

В случайные отклонения спроса в первом периоде могут могут принимать случайные значения из вектора [17, 18, 19, 20, 21], который представим в виде матрицы-столбца $Q_{1}$ :

Python

Q1 = np.c_[-2:3] + q1[x]
Q1

Результат

array([[17],
       [18],
       [19],
       [20],
       [21]])

Каждая корректирующая цена во втором периоде также может приводить к случайным отклонениям спроса во втором периоде, и все эти отклонения при определенной цене можно описать в виде строк следующей матрицы $Q_{2}$ :

Python

Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
Q2

Результат

Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
Q2
Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
Q2
array([[18, 19, 20, 21, 22],
       [18, 19, 20, 21, 22],
       [15, 16, 17, 18, 19],
       [15, 16, 17, 18, 19],
       [15, 16, 17, 18, 19]])

Данные вектор, столбец и матрица возможных отклонений показывают, какими могут быть комбинации отклонений спроса. Если отклонение в первом периоде будет равно 17, то мы выберем цену с индексом 0 из , т.е. 1.1. Матрица показывает, что при цене 1.1 спрос также может отклоняться и принимать значения из вектора [19, 20, 21, 22, 23] — первой строки матрицы $Q_{2}$ .

Теперь необходимо учесть ограничения по емкости самолета:

Python

Q2_trunc = np.where(Q1 + Q2 > 40, 40 - Q1, Q2)
Q2_trunc

Результат

array([[18, 19, 20, 21, 22],
       [18, 19, 20, 21, 22],
       [15, 16, 17, 18, 19],
       [15, 16, 17, 18, 19],
       [15, 16, 17, 18, 19]])

Вычислить возможные значения прибыли при разных комбинациях возможных значений спроса:

Python

Q1 * price[x] + Q2_trunc * np.c_[price[Y]]

Результ

array([[42. , 43.2, 44.4, 45.6, 46.8],
       [43.2, 44.4, 45.6, 46.8, 48. ],
       [43.8, 45.2, 46.6, 48. , 49.4],
       [45. , 46.4, 47.8, 49.2, 50.6],
       [46.2, 47.6, 49. , 50.4, 51.8]])

Умножить полученные значения на соответствующие вероятности их наблюдения и суммировать результат:

Python

prob_1 = np.full((5, 1), 0.2)
prob_2 = np.full((5, 5), 0.2)
np.sum((prob_1 * prob_2) * (Q1 * price[x] + Q2_trunc * np.c_[price[Y]]))

Результат

46.680000000000014

Поскольку для примера было выбрано равномерное дискретное распределение, то достаточно было найти среднее арифметическое возможных значений прибыли. Использование вероятностей показывает принцип определения средней прибыли при наличии других законов распределений. Выходит, что законы распределений никак не влияют на сложность оптимизации, так как в конечном итоге все равно придется работать с вероятностями отдельных значений и вычислять матожидания.

Итак, значение матожидания прибыли при выбранной цене в первом периоде и вектора корректирующих цен во втором периоде составляет 46.68. Мы можем также узнать и среднюю заполняемость самолета при выбранных и :

Python

np.sum((prob_1 * prob_2) * (Q1 + Q2_trunc))

Результат

37.20000000000001

Теперь проверим использование корректирующих цен с помощью эксперимента:

Python

def e_cp(x, Y):
    Q1 = np.c_[-2:3] + q1[x]
    Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
    Q2_trunc = np.where(Q1 + Q2 > 40, 40 - Q1, Q2)
    prob_1 = np.full((5, 1), 0.2)
    prob_2 = np.full((5, 5), 0.2)
    # e_occupancy = np.sum((prob_1 * prob_2) * (Q1 + Q2_trunc))
    e_profit = np.sum((prob_1 * prob_2) * (Q1 * price[x] + Q2_trunc * np.c_[price[Y]]))
    return e_profit

def sale_correct(price_1):
    n_iter = 5000
    test_data = []
    for _ in range(n_iter):
        q1 = demand(price_1, 0)
        
        if q1 in [17, 18]:
            price_2 = 1.2
        if q1 in [19, 20, 21]:
            price_2 = 1.4

        q2 = demand(price_2, 1)
        
        if q1 + q2 > 40:
            q2_correct = 40 - q1
            res_profit = q1 * price_1 + q2_correct * price_2
            test_data.append([q1 + q2, q1 + q2_correct, res_profit, 'larger capacity'])
        if q1 + q2 == 40:
            res_profit = q1 * price_1 + q2 * price_2
            test_data.append([q1 + q2, q1 + q2, res_profit, 'equal to capacity'])
        if q1 + q2 < 40:
            res_profit = q1 * price_1 + q2 * price_2
            test_data.append([q1 + q2, q1 + q2, res_profit, 'less capacity'])
            
    test_data_df = pd.DataFrame(test_data, 
                      columns=['demand', 'Q', 'profit', 'occupancy'])
            
    return test_data_df

data = sale_correct(price[x])

fig, ax = plt.subplots(1, 2, figsize=(12, 4))

sns.histplot(data=data, 
             x=data['demand'],
             hue='occupancy',
             hue_order=['less capacity', 'equal to capacity', 'larger capacity'],
             discrete=True,
             stat='probability',
             palette='Dark2',
             ax=ax[0])

ax[0].axvline(data.Q.mean(), color='r')
ax[0].set_xticks(np.r_[33:44])
ax[0].set_title('Aircraft occupancy\n(adjustment prices)')

sns.histplot(data.profit, bins=np.r_[41.01 : 51 : 1], stat='probability', ax=ax[1])
ax[1].axvline(data.profit.mean(), color='r')
ax[1].set_title('Distribution of profit values\n(adjustment prices)');

В первую очередь следует обратить внимание на то, что использование корректирующих цен не приводит к увеличению прибыли, но приводит к значительному уменьшению дисперсии заполняемости. Аналитические вычисления при этом более чем возможны, так как средние значения прибыли и заполняемости равны значениям, полученным теоретически.

Тем не менее, наличие возможности аналитических вычислений не означает, что с поиском оптимального вектора корректирующих цен все будет просто. Фактически перед нами возникает задача комбинаторной оптимизации, для которой будем использовать метод кросс-энтропии.

Для ее использования создадим несколько функций. Во-первых, нам понадобится функция, определяющая вероятностные распределения выборок с кандидатами на оптимальное решение:

Python

def hist_res(res_vals):
    bins = np.r_[0:6]

    h = np.array([np.histogram(res_vals.T[col],
                               bins=bins,
                               density=True)[0]
                  for col in range(5)])
    
    return h

'''
a = [0, 0, 0, 0, 0]
b = [5, 5, 5, 5, 5]
V = randint.rvs(low=a, high=b, size=(200, 5))

h = hist_res(V)
h
''';

Данная функция просто возвращает вероятности наблюдений определенных значений в соответствующих столбцах.

Следующая функция генерирует случайные значения в соответствии с полученными вероятностями:

Python

def rand_vec(h):
    indices = np.r_[0:5]
    
    vec = [np.random.choice(indices,
                            size=1
                            , p=h_i)[0]
           for h_i in h]
    
    return vec

# rand_vec(h)

И сама функция, выполняющая оптимизацию:

Python

def opt_price_vec(x):
    h = np.array([[0.2]*5]*5)
    
    while h.max(axis=1).sum() != 5:
        V = np.array([rand_vec(h) for _ in range(1000)])
        R = np.array([e_cp(x, v) for v in V])
        idx = np.argsort(R)[::-1][:50]
        h = hist_res(V[idx])
    opt_vec = np.nonzero(h)[1]
    return e_cp(x, opt_vec), opt_vec

Она принимает значение цены в первом периоде и выполняет поиск оптимального вектора цен для второго периода с учетом всех возможных отклонений.

Выясним значения максимальной средней прибыли для всех возможных цен в первом периоде:

Python

X = np.r_[:5]
res_e_profit = []
opt_vec = []

for x_i in X:
    solution = opt_price_vec(x_i)
    res_e_profit.append(solution[0])
    opt_vec.append(solution[1])

plt.plot(price, res_e_profit, 'o-')
plt.title('Dependence of maximum average profit\non price in the first period')
plt.ylabel('Average profit')
plt.xlabel(r'Price in $T_{1}$');

Ранее было показано, что $\mathrm{Price}^{(1)} = 1.1$ и $\mathrm{Price}^{(1)} = 1.2$ обеспечивают практически одинаковые средние прибыли, и сейчас это наблюдается повторно. Теперь взглянем на оптимальные векторы корректирующих цен:

Python

fig, ax = plt.subplots(1, 5, figsize=(12, 2.5))

for i in range(5):
    ax[i].plot(np.r_[:5], price[opt_vec[i]], 'o-')
    if i == 0:
        ax[i].set_ylabel(r'Price$^{(2)}$')
    ax[i].set_xlabel(r'$q^{(1)}$')
    ax[i].set_yticks(price)
    ax[i].set_xticks(np.r_[:5], np.r_[-2:3] + q1[i])
    ax[i].set_title(r'Price$^{(1)}$ = ' + str(price[i]))
    ax[i].set_ylim(1, 1.5)
    
plt.tight_layout()

fig.suptitle('Optimal vectors of adjustment prices',
             fontsize=15, y=1.05);

Таким способом и был получен оптимальный вектор $\mathrm{PriceVec}^{(2)} = (1.2, 1.2, 1.4, 1.4, 1.4)$ , который использовался в качестве примера выше.

Использование корректирующих цен не увеличивает средней прибыли, но снижает дисперсию итоговой заполняемости мест. В нашем примере используется всего два периода продаж, а если их будет больше? Многоэтапное стохастическое программирование зачастую показывает, что неоптимальные решения на первых этапах позволяют добиться значительно лучших результатов на последующих или заключительных этапах. В нашем случае возникает вполне естественный вопрос: могут ли отличаться оптимальные цены для первого этапа, найденные с корректирующими ценами и без них? Это возможно, но только в том случае, если распределения вероятностей на каком-то из этапов перестают быть унимодальными.

Возникает другой вопрос: могут ли значения спроса подчиняться, скажем, какому-нибудь бимодальному закону распределения? Наверное, на большом историческом промежутке времени такое возможно. Если же такое наблюдается на основе данных из недавнего прошлого, то модель спроса просто не учитывает какие-то факторы. Впрочем, даже если эти факторы в принципе невозможно учесть, то бимодальное распределение можно представить в виде смеси распределений, а значит искать корректирующие цены можно только после того, как будут найдены оптимальные цены для каждого из периодов.

В дальнейшем будем полагать, что все распределения используемые в модели спроса являются унимодальными.

1.4. Квоты

Отклонения спроса, как прогнозируемые, так и нет, могут быть очень большими. При резком движении спроса вверх какая-то значительная часть билетов может быть продана по невыгодной цене, либо билеты могут вовсе закончиться. По мере приближения даты вылета спрос, как правило, увеличивается. С помощью квот, ограничивающих продажу билетов по определенной цене некоторым фиксированным количеством, можно ограничить продажи на ранних этапах и сохранить больше билетов для их продажи в периодах, близких к вылету самолета, где они могут быть проданы по более выгодной цене. Очевидно, что использование квот более чем целесообразно, а их значения также должны быть оптимальными.

Обозначим квоту для первого периода символом $r^{(1)}$ и предположим, что значение квоты может быть равно одному из возможных значений спроса $q_{j}$ . Пусть равен 2, т.е. соответствует квоте в 19 кресел. А значения и будут теми же, что использовались в примере выше, т.е. оптимальные.

Python

# В данном случае u соответствует j
x, u, Y = 2, 2, [1, 1, 2, 2, 3]

В оптимизации по-прежнему нуждается уже знакомая целевая функция:

Поскольку введена квота $r^{(1)}$ , то теперь общее количество доступных к продаже билетов можно записать как:

$V = r^{(1)} + r^{(2)}.$

Единственное, но существенное отличие теперь связано с тем, что в системе ограничений появляется квота мест для количества проданных билетов в первом периоде:

$(q_{j}^{(1)}, r^{(1)}) = \begin{cases}(q_{j}^{(1)}, r^{(1)} - q_{j}^{(1)}), & \text{ if } q_{j}^{(1)} < r^{(1)} \\(r^{(1)}, 0), & \text{ if } q_{j}^{(1)} \geqslant r^{(1)}\end{cases}.$

Если в первом периоде будет продано меньше билетов, чем указано в квоте, то этот остаток необходимо учесть во втором периоде:

$q_{k}^{(2)} = \begin{cases}q_{k}^{(2)}, & \text{ if } q_{k}^{(2)} \leqslant r^{(2)} + r^{(1)} \\r^{(2)} + r^{(1)}, & \text{ if } q_{k}^{(2)} > r^{(2)} + r^{(1)}\end{cases}$

Отличие оптимизации в данном случае заключается только в том, что необходимо учитывать возможные значения , так что в использованные выше функции придется внести лишь небольшие изменения:

Python

def e_ucp(x, u, Y):
    Q1 = np.c_[-2:3] + q1[x]
    Q1[Q1 > Q1[u]] = Q1[u]
    Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
    Q2_trunc = np.where(Q1 + Q2 > 40, 40 - Q1, Q2)
    prob_1 = np.full((5, 1), 0.2)
    prob_2 = np.full((5, 5), 0.2)
    # e_occupancy = np.sum((prob_1 * prob_2) * (Q1 + Q2_trunc))
    e_profit = np.sum((prob_1 * prob_2) * (Q1 * price[x] + Q2_trunc * np.c_[price[Y]]))
    return e_profit

def opt_price_vec(x, u):
    h = np.array([[0.2]*5]*5)
    
    while h.max(axis=1).sum() != 5:
        V = np.array([rand_vec(h) for _ in range(1000)])
        R = np.array([e_ucp(x, u, v) for v in V])
        idx = np.argsort(R)[::-1][:50]
        h = hist_res(V[idx])
    opt_vec = np.nonzero(h)[1]
    return e_ucp(x, u, opt_vec), u, opt_vec

Теперь попробуем определить оптимальные квоты и векторы корректирующих цен для каждой цены в первом периоде:

Python

q1

Результат

array([23, 21, 19, 17, 15])

Python

q1 = np.round(-20 * price + 43).astype(int)
q2 = np.round(-15 * price + 38).astype(int)
res_xu = []
for x_i in range(5):
    Q1 = np.r_[-2:3] + q1[x_i]
    res_xu_row = []
    #print('-' * 100)
    #print('x_i =', x_i)
    for u_j in range(5):
        vec_price = opt_price_vec(x_i, u_j)
        res_xu_row.append([Q1[vec_price[1]], vec_price[0]])
        # print(x_i, vec_price)
    res_xu.append(res_xu_row)
    
res_xu = np.array(res_xu)

for i in range(5):
    plt.plot(res_xu[i][:, 0], res_xu[i][:, 1], 'o-', label=str(price[i]))

plt.legend(title=r'Price$^{(1)}$')
plt.ylabel('Average profit')
plt.xlabel(r'quota for the $q^{(1)}$')
plt.xticks(np.r_[13:26])
plt.title('Dependence of average profit\non the size of the quota of places in the first period');

О едва заметной пользе введения квот можно сказать только в том случае, если в первом периоде используется цена 1.1. Во всех остальных случаях любое ограничение возможных отклонений приводит лишь к явному снижению средней прибыли.

Хотелось бы убедиться в том, что квоты действительно могут оказывать сильное влияние на среднюю прибыль. Предположим, что распределение спроса в первом периоде при оптимальном сильно сместилось вверх, например, теперь отклонения могут принимать значения из [23, 24, 25, 26, 27], а не [17, 18, 19, 20, 21]. В этом случае увидим следующее:

Python

q1 = np.round(-20 * price + 43).astype(int)
q2 = np.round(-15 * price + 38).astype(int)
res_xu = []
for x_i in range(5):
    Q1 = np.r_[-2:3] + q1[x_i]
    res_xu_row = []
    #print('-' * 100)
    #print('x_i =', x_i)
    for u_j in range(5):
        vec_price = opt_price_vec(x_i, u_j)
        res_xu_row.append([Q1[vec_price[1]], vec_price[0]])
        # print(x_i, vec_price)
    res_xu.append(res_xu_row)
    
res_xu = np.array(res_xu)

def e_ucp(x, u, Y):
    Q1 = np.c_[-2:3] + q1[x]
    if x == 2:
        Q1 = np.array([[23], [24], [25], [26], [27]])
    Q1[Q1 > Q1[u]] = Q1[u]
    Q2 = (np.tile(np.c_[-2:3], (1, 5)) + q2).T[Y]
    Q2_trunc = np.where(Q1 + Q2 > 40, 40 - Q1, Q2)
    prob_1 = np.full((5, 1), 0.2)
    prob_2 = np.full((5, 5), 0.2)
    # e_occupancy = np.sum((prob_1 * prob_2) * (Q1 + Q2_trunc))
    e_profit = np.sum((prob_1 * prob_2) * (Q1 * price[x] + Q2_trunc * np.c_[price[Y]]))
    return e_profit

q1 = np.round(-20 * price + 43).astype(int)
q2 = np.round(-15 * price + 38).astype(int)

res_xu = []
for x_i in range(5):
    Q1 = np.r_[-2:3] + q1[x_i]
    if x_i == 2:
        Q1 = np.array([23, 24, 25, 26, 27])
    res_xu_row = []
    #print('-' * 100)
    #print('x_i =', x_i)
    for u_j in range(5):
        vec_price = opt_price_vec(x_i, u_j)
        res_xu_row.append([Q1[vec_price[1]], vec_price[0]])
        #print(x_i, vec_price)
    res_xu.append(res_xu_row)
    
res_xu = np.array(res_xu)

for i in range(5):
    plt.plot(res_xu[i][:, 0], res_xu[i][:, 1], 'o-', label=str(price[i]))

plt.legend(title=r'Price$^{(1)}$')
plt.ylabel('Average profit')
plt.xlabel(r'quota for the $q^{(1)}$')
plt.xticks(np.r_[13:36])
plt.title('Dependence of average profit\non the size of the quota of places in the first period');

Из-за смещения распределения средняя прибыль очень сильно возросла, при этом также видно, что квота действительно сработала. В данном случае лучшая квота для количества билетов, продаваемых в первом периоде по цене 1.2, составляет 25 кресел.

Квоты помогают отсечь длинные хвосты распределений спроса, но, поскольку отклонения случайны и могут сильно отклоняться как вверх, так и вниз, то квоты могут быть исчерпаны не полностью. В нашем примере используется всего два периода продаж, а если периода будет уже три, то эти остатки нужно как-то перераспределять и делать это нужно также — оптимально.

2. Простейшие варианты нестинга и его оптимизация

В гражданской авиации цена ассоциируется с классом бронирования, или подклассом, которые обозначаются заглавными латинскими буквами. Класс обслуживания и класс бронирования — разные понятия. Например, "БИЗНЕС" — это класс обслуживания, который авиакомпания может разбить на три подкласса бронирования: J, C и D, при этом вовсе не значит, что в этих трех подклассах различный уровень комфорта или сервиса. Единственное, чем они могут отличаться, так это ценой (тарифами, в которых и указывается стоимость предоставления услуги по перевозке). В тарифе также можно прописать и некоторые другие условия: например, подкласс J может продаваться только за 3 дня до вылета, а подкласс C — только в период с 7 до 3 дней до вылета.

Выходит, что авиакомпании не могут использовать динамическое ценообразование в полной мере, потому что изменение тарифов (в которых указывается цена билетов) не может быть выполнено мгновенно. Это заставляет авиакомпании планировать продажи заранее. Например, авиакомпания может оценить спрос и решить, что:

в период c 10-ти до 3-х дней до вылета нужно продавать 18 билетов подкласса D по цене 110 у.е.;
в период c 3-х до 1-го дней до вылета нужно продавать 14 билетов подкласса C по цене 120 у.е.;
за день до вылета нужно продать 8 билетов подкласса J по цене 140 у.е.

В общем план опирается на классическое определение спроса и должен включать в себя:

периоды, которые могут быть указаны в днях:
- $T_{1} = [10, 3)$ ;
- $T_{2} = [3, 1)$ ;
- $T_{3} = [1, 0.05]$ .
цены:
- D = 110 у.е.;
- C = 120 у.е.;
- J = 140 у.е..
квоты мест:
- D = 18 билетов;
- С = 14 билетов;
- J = 8 билетов.

На простом примере выше было показано, что введение квот действительно целесообразно и приводит к максимизации прибыли. Однако возникающие остатки необходимо как-то перераспределять между подклассами: в случае появления остатков мест в подклассе D эти самые остатки можно отдать, например, в подкласс C или J. С другой стороны, корректирующие цены также являются очень полезными, а значит, несмотря на наличие всего трех периодов, авиакомпания может ввести больше подклассов, например, к имеющимся трем добавить еще подклассы I и Z. Какие-то подклассы могут быть не использованы вовсе, но так как у них тоже есть квоты, то необходимо указать какому подклассу будут отданы их места в этом случае.

Чтобы справиться с перераспределением остатков между подклассами и вести перерасчет мест, авиакомпании используют нестинг. Упрощенно нестинг можно представить как механизм, который определяет иерархию подклассов (цен) и правила перерасчета квот, т.е. доступных к продаже мест по определенной цене в случае, если в подклассах появляются остатки или какие-то подклассы не используются.

Звучит очень логично, но, с точки зрения моделирования спроса, введение квот означает, что продажи в текущем периоде могут прекратиться раньше, чем предполагалось. Это значит, что либо какое-то время билетов нет в продаже (чего быть не должно), либо последующий период начнется раньше — распределение спроса в нем будет не таким, как предполагалось, т.е. условным и зависеть от времени окончания продаж в предыдущем периоде.

Чтобы разобраться с нестингом, необходима более сложная модель спроса. И на самом деле их может быть даже две. Первая модель уже использовалась выше: в ней авиакомпания видит только количество проданных билетов в определенном периоде по некоторой цене.

Допустим, имеется всего три периода: $T_{1}$ , $T_{2}$ , $T_{3}$ и три кривых спроса: $f_{1}(\mathrm{price})$ , $f_{2}(\mathrm{price})$ , $f_{2}(\mathrm{price})$ :

Python

price = np.round(price, 1)
mu1 = np.array([22, 20, 17, 14, 8])
mu2 = np.array([24, 21, 19, 15, 11])
mu3 = np.array([21, 19, 18, 17, 16])

plt.plot(price, mu1, 'bo-', label=r'$T_{1}$')
plt.plot(price, mu2, 'ro-', label=r'$T_{2}$')
plt.plot(price, mu3, 'go-', label=r'$T_{3}$')
plt.xlabel('price')
plt.ylabel('demand')
plt.title('Dependence of demand on price and period')

plt.legend();

Данные функции показывают матожидания количества проданных билетов по определенной цене в каждом периоде. Количество проданных билетов — случайная величина, которая может испытывать отклонения. Если бы авиакомпания могла выполнить повтор третьего периода $T_{3}$ бесчисленное количество раз и продавать в нем билеты по цене 1.2, то все возможные количества проданных билетов могли бы быть описаны некоторым распределением, скажем, распределением Пуассона:

Python

mu = 18
Q = np.arange(5, 35)

plt.stem(Q, poisson.pmf(Q, mu), label='poisson pmf')
plt.xlabel('Demand')
plt.ylabel('Probability')
plt.title(r'Distribution of demand in the $T_{3}$ at price 1.2')
plt.legend();

Причем для разных цен эти распределения будут разными:

Python

P1 = poisson.pmf(Q, mu1.reshape(5, 1))
P2 = poisson.pmf(Q, mu2.reshape(5, 1))
P3 = poisson.pmf(Q, mu3.reshape(5, 1))
for t in range(5):
    plt.plot(Q, P3[t], 'o-', ms=4, label=str(price[t]))
plt.legend(title='Price:')
plt.xlabel('Demand')
plt.ylabel('Probability')
plt.title('Demand distributions in the third period');

Тем не менее, спрос лучше воспринимать как некоторую поверхность. Можно нарисовать кривые спроса вместе с распределениями в виде тепловой карты для каждого периода:

Python

fig, ax = plt.subplots(1, 3, figsize=(12, 4), sharex=True, sharey=True)
cbar_ax = fig.add_axes([.15, -.07, .7, .05])
cbar_ax.set_title('Probability', y=-2.3)
P1_df = pd.DataFrame(P1.T[::-1], index=Q[::-1],
                     columns=price)

sns.heatmap(P1_df, cmap='copper', cbar_ax=cbar_ax, cbar_kws={'orientation':'horizontal'}, ax=ax[0])
ax[0].plot(np.r_[0.5:5.5:1], 35 - mu1, 'o-', c='darkred', label='f1')
ax[0].set_xlabel('Price')
ax[0].set_ylabel('Demand')
ax[0].legend()
ax[0].set_title(r'Demand distributions in the $T_{1}$')

P2_df = pd.DataFrame(P2.T[::-1], index=Q[::-1],
                     columns=price)
sns.heatmap(P2_df, cmap='copper', cbar=False, ax=ax[1])
ax[1].plot(np.r_[0.5:5.5:1], 35 - mu2, 'o-', c='darkred', label='f2')
ax[1].set_xlabel('Price')
ax[1].set_ylabel('Demand')
ax[1].legend()
ax[1].set_title(r'Demand distributions in the $T_{2}$')

P3_df = pd.DataFrame(P3.T[::-1], index=Q[::-1],
                     columns=price)
sns.heatmap(P3_df, cmap='copper', cbar=False, ax=ax[2])
ax[2].plot(np.r_[0.5:5.5:1], 35 - mu3, 'o-', c='darkred', label='f3')
ax[2].set_xlabel('Price')
ax[2].set_ylabel('Demand')
ax[2].legend()
ax[2].set_title(r'Demand distributions in the $T_{3}$');

Если наложить такие тепловые карты друг на друга, то получится поверхность, точки которой испытывают случайные отклонения по оси показывающей величину спроса. По сути это — типичная регрессионная модель, которую можно использовать как прогнозную. Данная модель обладает целым рядом важных особенностей.

В данном примере случайные отклонения спроса ничем не объясняются и могут восприниматься как шум. Отклонения могут быть вызваны самыми разными факторами (например, ценой на туристические путевки). Включение некоторого фактора переводит модель из трехмерного пространства в четырехмерное, а точки гиперповерхности будут испытывать меньшие отклонения, поскольку какая-то часть отклонений теперь объяснена этим новым фактором. Нетрудно догадаться, что чем меньше отклонения (дисперсия, неопределенность), тем меньше вычислений для последующей оптимизации.

Создание модели спроса — это задача машинного обучения, качество которой зависит от данных. Тут действует старое правило: мусор на входе — мусор на выходе. Плохая модель может свести на нет все попытки последующей оптимизации.

Другая особенность модели связана с тем, что авиакомпания не может себе позволить эксперименты с ценами, чтобы получить больше данных для уточнения модели. Фреквентистский подход в данном случае — это плохая идея. Он плох тем, что оперирует неопределенностью напрямую, посредством обработки экспериментов: чем больше экспериментов, тем лучше информация о неопределенности (распределении возможных отклонений спроса). Информация о неопределенности спроса при этом — это главное "топливо" для последующей оптимизации.

Байесовский вывод работает с неопределенностью спроса косвенно. В фреквентистском подходе параметры модели имеют четкое значение, в байесовском они сами рассматриваются как случайные величины с собственными распределениями. Это решает проблему объема данных, которых потребуется гораздо меньше.

Еще одна особенность связана с тем, что модель зависит от интервалов времени, а не от времени. Именно по этой причине эта модель и была названа интегральной. Создание интегральной модели — отнюдь непростая задача, ведь цены и квоты цензурируют наблюдения, а границы периодов продаж из-за квот также будут испытывать отклонения. Однако благодаря вероятностному программированию можно создать дифференциальную модель спроса — она показывает, как вероятность покупки билета отдельным потенциальным клиентом зависит от цены и времени.

Информация о том, сколько человек интересовались покупкой билета и сколько из них его купили, имеет особую важность для создания дифференциальных моделей. Дифференциальные модели во многом лучше и могут даже рассматриваться как порождающие интегральные модели.

Например, зависимость вероятности появления потенциального покупателя от времени до вылета самолета может быть задана некоторым распределением. Для простоты возьмем гамма распределение:

$P(d|t) \sim \Gamma (0.9, 3)$

Python

f, ax = plt.subplots(1, 2, figsize=(12, 3.5))

x = np.linspace(0, 10)
y = gamma.pdf(x, a=0.9, scale=3)
ax[0].plot(x, y)
ax[0].set_ylabel(r'$P(d|t)$')
ax[0].set_xlabel('t (day)')
ax[0].set_title(r'$P(d|t) \sim \Gamma (0.9, 3)$')

t = gamma.rvs(a=0.9, scale=3, size=100)
t = t[t < 10]
sns.histplot(t, ax=ax[1], bins=np.r_[:10])
ax[1].set_xlabel('t (day)')
ax[1].set_title('Dependence of the number of potential buyers\non the time interval');

Первый график показывает, что вероятность появления покупателя за 10 дней до вылета гораздо меньше, чем за 5, и крайне высока за несколько часов до него. Второй график показывает, что количество потенциальных покупателей в разные интервалы времени может выглядеть совершенно по-разному. В данном случае показано распределение потенциальных покупателей для рейса, по которому желает лететь в среднем 100 человек.

Если известно количество потенциальных покупателей, а также сколько из них покупает билет по определенной цене, то благодаря вероятностному программированию возможно определить вероятность покупки билета, которая будет зависеть не от периода продаж и цены, а от времени продажи и цены. Эта зависимость может быть выражена бетабиномиальным распределением :

Python

f, ax = plt.subplots(1, 2, figsize=(12, 3.5))

x = np.arange(5)
n, a, b = 4, 1, 0.99*9 + 0.1

ax[0].plot(x, betabinom.pmf(x, n, a, b), 'bo', ms=8, label='betabinom pmf')
ax[0].vlines(x, 0, betabinom.pmf(x, n, a, b), colors='b', lw=5, alpha=0.5)
ax[0].set_xticks(x, map(str, price))
ax[0].set_xlabel('Price')
ax[0].set_ylabel('Probability')
ax[0].set_title('Dependence of the probability of purchasing a ticket\non the price 9 days before departure')

n, a, b = 4, 1, 0.99*1 + 0.1

ax[1].plot(x, betabinom.pmf(x, n, a, b), 'bo', ms=8, label='betabinom pmf')
ax[1].vlines(x, 0, betabinom.pmf(x, n, a, b), colors='b', lw=5, alpha=0.5)
ax[1].set_xticks(x, map(str, price))
ax[1].set_xlabel('Price')
ax[1].set_ylabel('Probability')
ax[1].set_title('Dependence of the probability of purchasing a ticket\non the price 1 day before departure');

График показывает, что за 9 дней до вылета вероятность покупки при большой цене практически равна 0, в то время как за один день до вылета — достаточно велика. Однако, поскольку один из параметров в этом распределении зависит от времени, то приведенная интегральная модель покажет, что за все 10 дней продаж распределение количества покупателей, готовых купить по определенной цене, будет выглядеть несколько неожиданным образом:

Python

t = np.sort(gamma.rvs(a=0.9, scale=3, size=10000))[::-1]
t = t[t < 10]
price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
demand = price[price_idx]
sns.histplot(demand, bins=np.r_[0.95:1.5:0.1], stat='probability')
plt.xlabel('price')
plt.title('pmf of purchasing a ticket at a certain price for all 10 days');

Данную модель в дальнейшем будем использовать для моделирования "реальности", поскольку она действительно является порождающей интегральную. Пусть первый период будет занимать интервал времени от 10 до 3-х дней до вылета, в котором проверим, какие могут быть отклонения спроса при разных ценах:

Python

fig, ax = plt.subplots(1, 5, figsize=(15, 3))
mu_t1 = []
for i in range(5):
    dem1 = []
    for _ in range(1000):
        t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
        t = t[t < 10]
        price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
        demand = price[price_idx]
        end_t1 = np.where(t > 3)[0][-1]
        dem1.append(np.cumsum(demand[: end_t1 + 1] >= price[i])[-1])
    mu_t1.append(np.mean(dem1))
    xx = np.arange(poisson.ppf(0.001, mu_t1[-1]),
                   poisson.ppf(0.999, mu_t1[-1]))
    yy = poisson.pmf(xx, mu_t1[-1])
    ax[i].set_title(f'price = {price[i]}')
    ax[i].plot(xx, yy, 'bo', ms=3, label=rf'$\mu$ = {mu_t1[-1]}')
    ax[i].legend()
    ax[i].vlines(xx, 0, yy, colors='b', lw=1, alpha=0.5)

    sns.histplot(dem1, discrete=True, stat='density', ax=ax[i])
fig.suptitle(r'Period $T_{1}=[10, 3)$')
plt.tight_layout();

На гистограммы нанесены точки, соответствующие пуассоновскому распределению с $\mu$ (средней интенсивностью), равной среднему значению всех возможных значений спроса. Отклонения хорошо аппроксимируются Пуасоновским распределением, что неудивительно, так как каждая гистограмма показывает распределение возможного числа покупок билетов за фиксированный период времени $T_{1}$ .

Проделаем то же самое для второго периода, который будет занимать время с 3-го по 1-й день до вылета:

Python

fig, ax = plt.subplots(1, 5, figsize=(15, 3))
mu_t2 = []
for i in range(5):
    dem2 = []
    for _ in range(1000):
        t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
        t = t[t < 10]
        price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
        demand = price[price_idx]
        start_t2 = np.where(t > 3)[0][-1]
        end_t2 = np.where(t > 1)[0][-1]
        dem2.append(np.sum(demand[start_t2 : end_t2 + 1] >= price[i]))
    mu_t2.append(np.mean(dem2))
    xx = np.arange(poisson.ppf(0.001, mu_t2[-1]),
                   poisson.ppf(0.999, mu_t2[-1]))
    yy = poisson.pmf(xx, mu_t2[-1])
    ax[i].set_title(f'price = {price[i]}')
    ax[i].plot(xx, yy, 'bo', ms=3, label=rf'$\mu$ = {mu_t2[-1]}')
    ax[i].legend()
    ax[i].vlines(xx, 0, yy, colors='b', lw=1, alpha=0.5)

    sns.histplot(dem2, discrete=True, stat='density', ax=ax[i])
#print(mu_t2)
fig.suptitle(r'Period $T_{2}=[3, 1)$')
plt.tight_layout();

Чем меньше цена (и больше $\mu$ ), тем хуже аппроксимация. Это связано с зависимостью вероятности покупки билета от времени. В случае, если предполагается использование только очень низких цен, то это проблема. Однако крайне трудно представить такую ситуацию, поэтому можно вполне уверенно полагаться на распределение Пуассона.

Для третьего периода, который займет оставшееся время, имеем следующую картину:

Python

fig, ax = plt.subplots(1, 5, figsize=(15, 3))
mu_t3 = []
for i in range(5):
    dem3 = []
    for _ in range(1000):
        t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
        t = t[t < 10]
        price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
        demand = price[price_idx]
        start_t3 = np.where(t > 1)[0][-1]
        dem3.append(np.sum(demand[start_t3 + 1 : ] >= price[i]))

    mu_t3.append(np.mean(dem3))
    xx = np.arange(poisson.ppf(0.001, mu_t3[-1]),
                   poisson.ppf(0.999, mu_t3[-1]))
    yy = poisson.pmf(xx, mu_t3[-1])
    ax[i].set_title(f'price = {price[i]}')
    ax[i].plot(xx, yy, 'bo', ms=3, label=rf'$\mu$ = {mu_t3[-1]}')
    ax[i].legend()
    ax[i].vlines(xx, 0, yy, colors='b', lw=1, alpha=0.5)

    sns.histplot(dem3, discrete=True, stat='density', ax=ax[i])
#print(mu_t3)
fig.suptitle(r'Period $T_{3}$')
plt.tight_layout();

Как видим, дифференциальная модель, которая рассматривает каждого отдельного потенциального клиента, действительно может быть использована для моделирования массовых явлений. В конечном итоге, если изобразить зависимость $\mu$ от цены в каждом периоде, то получатся кривые спроса:

Python

plt.plot(price, mu_t1, 'ro-', label=r'$T_{1}$')
plt.plot(price, mu_t2, 'go-', label=r'$T_{2}$')
plt.plot(price, mu_t3, 'bo-', label=r'$T_{3}$')
plt.legend()
plt.xlabel('Price')
plt.ylabel('Mean demand')
plt.title('Demand curves derived from a differential demand model');

Теперь предположим, что некоторая авиакомпания обладает только что полученной интегральной моделью и решила провести оптимизацию продаж на ее основе. Пусть будет всего три подкласса бронирования: J, C и D, где J — самый дорогой подкласс, D — самый дешевый, а в самолете всего 40 мест.

Python

def profit_poisson(x):
    
    q1 = poisson.rvs(mu=mu_t1[x[0]])
    if q1 > 40:
        q1 = 40
        q2 = 0
        q3 = 0
    else:
        q2 = poisson.rvs(mu=mu_t2[x[1]])
        if q1 + q2 > 40:
            q2 = 40 - q1
            q3 = 0
        else:
            q3 = poisson.rvs(mu=mu_t3[x[2]])
            if q1 + q2 + q3 > 40:
                q3 = 40 - q1 - q2
                
    profit = q1 * price[x[0]] + q2 * price[x[1]] + q3 * price[x[2]]
    return profit

def e_profit_poisson(x):
    return np.mean([profit_poisson(x) for _ in range(300)])

def hist_res_x(res_vals):
    bins = np.r_[0:6]
    h = np.array([np.histogram(res_vals.T[col],
                               bins=bins,
                               density=True)[0]
                  for col in range(3)])
    
    return h

def rand_vec_x(h):
    indices = np.r_[0:5]
    
    vec = [np.random.choice(indices,
                            size=1
                            , p=h_i)[0]
           for h_i in h]
    
    return vec

def opt_price_vecs(n_iter):
    h_x = np.array([[0.2]*5]*3)
    c_iter = 0
    while h_x.max(axis=1).sum() != 3:
        V_X = np.array([rand_vec_x(h_x) for _ in range(n_iter)])
        R = np.array([e_profit_poisson(V_X[i]) for i in range(n_iter)])
        idx = np.argsort(R)[::-1][:30]
        h_x = hist_res_x(V_X[idx])
        print(np.argmax(h_x, axis=1))
        print('-'*30)
        c_iter += 1
        if c_iter == 7:
            break
    opt_price = price[np.nonzero(h_x)[1]]
    print('opt_price =', opt_price)
    x = np.argmax(h_x, axis=1)
    return e_profit_poisson(x), x

opt_price_vecs(100)

Результат

[1 2 3]
------------------------------
[1 2 2]
------------------------------
[1 2 3]
------------------------------
[1 2 3]
------------------------------
opt_price = [1.1 1.2 1.3]
(47.53566666666667, array([1, 2, 3], dtype=int64))

Наилучшими ценами для каждого из периодов оказались значения 1.1, 1.2, 1.3.

Благодаря дифференциальной модели можно выяснить, к чему приведет использование данных цен в "реальности":

Python

def profit_real(x):
    
    t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
    t = t[t < 10]
    price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
    demand = price[price_idx]

    end_t1 = np.where(t > 3)[0][-1]
    q1_cumsum = np.cumsum(demand[: end_t1 + 1] >= price[x[0]])
    idx_u1 = np.where(q1_cumsum == 40)[0]
    if idx_u1.size != 0:
        end_t1 = idx_u1[0]
        q1 = q1_cumsum[end_t1]
        q2 = 0
        q3 = 0
        end_t2 = end_t1
        end_t3 = end_t1
    else:
        q1 = q1_cumsum[end_t1]
        
        end_t2 = np.where(t > 1)[0][-1]
        q2_cumsum = np.cumsum(demand[end_t1 + 1 : end_t2 + 1] >= price[x[1]])
        idx_u2 = np.where(q2_cumsum == (40 - q1))[0] + end_t1 + 1
        if idx_u2.size != 0:
            end_t2 = idx_u2[0]
            q2 = q2_cumsum[end_t2 - end_t1 - 1]
            q3 = 0
            end_t3 = end_t2
        else:
            q2 = q2_cumsum[end_t2 - end_t1 - 1]
            
            q3_cumsum = np.cumsum(demand[np.where(t < t[end_t2])[0]] >= price[x[2]])
            idx_u3 = np.where(q3_cumsum == (40 - q1 - q2))[0] + end_t2 + 1
            if idx_u3.size != 0:
                end_t3 = idx_u3[0]
                q3 = q3_cumsum[end_t3 - end_t2 - 1]
            else:
                end_t3 = t.size - 1
                q3 = q3_cumsum[end_t3 - end_t2 - 1]

    profit = q1 * price[x[0]] + q2 * price[x[1]] + q3 * price[x[2]]

    return profit , q1, q2, q3, q1 + q2 + q3, t[end_t1], t[end_t2], t[end_t3]

x = [1, 2, 3]
#profit_real(x)

sales_real = [profit_real(x) for _ in range(3000)]
sales_real_df = pd.DataFrame(sales_real,
                columns=['profit', 'D', 'C', 'J', 'All',
                         'end_t1', 'end_t2', 'end_t3']
               )
#sales_real_df.head()

Распределение средней прибыли будет выглядеть следующим образом:

Python

sns.histplot(sales_real_df.profit)
E_p = sales_real_df.profit.mean()
plt.axvline(E_p, color='r', label=f'E(Profit) = {E_p:.2f}')
plt.legend()
plt.title('Average profit distribution');

Так будет выглядеть заполняемость соответствующих подклассов:

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_real_df.D, discrete=True, ax=ax[0])
ax[0].set_title('D (price = 1.1)')
ax[0].set_xlabel('Occupancy')
sns.histplot(sales_real_df.C, discrete=True, ax=ax[1])
ax[1].set_title('C (price = 1.2)')
ax[1].set_xlabel('Occupancy')
sns.histplot(sales_real_df.J, discrete=True, ax=ax[2])
ax[2].set_title('J (price = 1.3)')
ax[2].set_xlabel('Occupancy')
plt.tight_layout();

Все выглядит довольно неплохо, но если взглянуть на время окончания каждого периода, то уже не все так, как нам хотелось бы:

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_real_df.end_t1, ax=ax[0])
e_t1 = sales_real_df.end_t1.mean()
ax[0].axvline(e_t1, color='r', label=f'E(end_t1) = {e_t1:.2f}')
ax[0].legend()
ax[0].set_title('End of period T1 (D sales)')
ax[0].set_xlabel('Day')
sns.histplot(sales_real_df.end_t2, ax=ax[1])
e_t2 = sales_real_df.end_t2.mean()
ax[1].axvline(e_t2, color='r', label=f'E(end_t2) = {e_t2:.2f}')
ax[1].legend()
ax[1].set_title('End of period T2')
ax[1].set_xlabel('Day')
sns.histplot(sales_real_df.end_t3, ax=ax[2])
e_t3 = sales_real_df.end_t3.mean()
ax[2].axvline(e_t3, color='r', label=f'E(end_t3) = {e_t3:.2f}')
ax[2].legend()
ax[2].set_title('End of period T3')
ax[2].set_xlabel('Day')
plt.tight_layout();

В идеале время окончания периода $T_{3}$ (т.е. завершение продаж авиабилетов) должно располагаться как можно ближе к времени вылета. Однако, судя по графику, окончание продаж за 12 часов до вылета — вполне обычная ситуация, что очень плохо.

Использование квот оказывает положительный эффект, позволяя ограничить слишком большие отклонения спроса и не продавать слишком много билетов по низким ценам. Теперь задумаемся над тем, что использование квот для каждого из подклассов предполагает наличие остатков: если мы ввели для подкласса D квоту в 12 мест, а продали всего 10, то останется 2. И вот этот остаток нужно куда-то деть — прибавить его либо к квоте подкласса C, либо к квоте подкласса J. Именно тут и необходимо применить нестинг.

Нестинг позволяет установить иерархию подклассов, а вместе с ней правила перерасчета мест в каждом из них. Можно установить квоты для подклассов D и С, а также задать правило, согласно которому нераспроданные билеты в подклассе D будут прибавлены к квоте подкласса C. А подкласс J будет равен оставшемуся количеству мест, включая остаток подкласса C. Описанный тип нестинга называется линейным.

Попробуем найти наилучшие цены для для подклассов, а также наилучшие значения квот при данном варианте нестинга.

Python

# Функция моделирующая продажи на основе время-зависимой
# модели спроса, иерархии подклассов и правила переасчета мест:

def profit_lin(X, Up):
    
    U = np.copy(Up)
    t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
    t = t[t < 10]
    price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
    demand = price[price_idx]

    end_t1 = np.where(t > 3)[0][-1]
    q1_cumsum = np.cumsum(demand[: end_t1 + 1] >= X[0])
    idx_u1 = np.where(q1_cumsum == U[0])[0]
    if idx_u1.size != 0:
        end_t1 = idx_u1[0]
        q1 = q1_cumsum[end_t1]
    else:
        q1 = q1_cumsum[end_t1]

    U[1] = U[1] + U[0] - q1

    end_t2 = np.where(t > 1)[0][-1]
    q2_cumsum = np.cumsum(demand[end_t1 + 1 : end_t2 + 1] >= X[1])
    idx_u2 = np.where(q2_cumsum == U[1])[0] + end_t1 + 1
    if idx_u2.size != 0:
        end_t2 = idx_u2[0]
        q2 = q2_cumsum[end_t2 - end_t1 - 1]
    else:
        q2 = q2_cumsum[end_t2 - end_t1 - 1]

    U[2] = 40 - q1 - q2

    q3_cumsum = np.cumsum(demand[np.where(t < t[end_t2])[0]] >= X[2])
    idx_u3 = np.where(q3_cumsum == U[2])[0] + end_t2 + 1
    if idx_u3.size != 0:
        end_t3 = idx_u3[0]
        q3 = q3_cumsum[end_t3 - end_t2 - 1]
    else:
        end_t3 = t.size - 1
        q3 = q3_cumsum[end_t3 - end_t2 - 1]

    profit = q1 * X[0] + q2 * X[1] + q3 * X[2]

    return profit, q1, q2, q3, q1 + q2 + q3, t[end_t1], t[end_t2], t[end_t3]

#X = np.array([1.1, 1.2, 1.3])
#Up = np.array([9, 9, 40])
#profit_lin(X, Up)

# Функция, вычисляющая среднюю прибыль:
def e_profit_lin(X, Up, n_iter):
    return np.mean([profit_lin(X, Up)[0] for _ in range(n_iter)])

#e_profit_lin(X, Up, 10000)

# ряд вспомогательных функций для оптимизации методом кросс-энтропии:
def hist_res_x(res_vals):
    bins = np.r_[0:6]
    h = np.array([np.histogram(res_vals.T[col],
                               bins=bins,
                               density=True)[0]
                  for col in range(3)])
    
    return h

def rand_vec_x(h):
    indices = np.r_[0:5]
    
    vec = [np.random.choice(indices,
                            size=1
                            , p=h_i)[0]
           for h_i in h]
    
    return vec

def hist_res_u(res_vals):
    bins = np.r_[1:22]
    h = np.array([np.histogram(res_vals.T[col],
                               bins=bins,
                               density=True)[0]
                  for col in range(2)])
    
    return h

def rand_vec_u(h):
    indices = np.r_[1:21]
    
    vec = [np.random.choice(indices,
                            size=1
                            , p=h_i)[0]
           for h_i in h]
    
    return vec + [40]

# Функция выполняющая оптимизацию:
def opt_price_vecs(n_iter):
    h_x = np.array([[0.2]*5]*3)
    h_u = np.array([[0.05]*20]*2)
    c_iter = 0
    while h_u.max(axis=1).sum() != 2:
        V_X = np.array([rand_vec_x(h_x) for _ in range(n_iter)])
        V_U = np.array([rand_vec_u(h_u) for _ in range(n_iter)])
        R = np.array([e_profit_lin(price[V_X[i_vec]], V_U[i_vec], 200) for i_vec in range(n_iter)])
        idx = np.argsort(R)[::-1][:20]
        h_x = hist_res_x(V_X[idx])
        h_u = hist_res_u(V_U[idx])
        print(np.argmax(h_x, axis=1))
        print(np.argmax(h_u, axis=1))
        print('-'*30)
        c_iter += 1
        if c_iter == 7:
            break
    opt_vec_x = price[np.nonzero(h_x)[1]]
    opt_vec_u = np.hstack((np.argmax(h_u, axis=1), [40]))
    print(opt_vec_x, opt_vec_u)
    return e_profit_lin(opt_vec_x, opt_vec_u, 200)

opt_price_vecs(200)

Python

[1 2 3]
[18  8]
------------------------------
[1 2 3]
[17  8]
------------------------------
[1 2 3]
[10 10]
------------------------------
[1 2 3]
[10 10]
------------------------------
[1 2 3]
[ 7 10]
------------------------------
[1 2 3]
[ 7 10]
------------------------------
[1 2 3]
[ 7 10]
------------------------------
[1.1 1.2 1.3] [ 7 10 40]
48.27900000000002

Оптимальные цены получились теми же самыми, но теперь есть оптимальные значения для квот:

D — 7 мест;
C — 10 мест;
J — забирает все оставшиеся места.

Необходимо сразу отметить, что используемый метод оптимизации может выдавать разные значения для квот, при этом значения средней прибыли могут практически не меняться. Это настораживает, и с этим нужно разобраться.

Поскольку используемая для примера модель спроса не так сложна, то можно вычислить значения средней прибыли для всех возможных значений квот при оптимальных ценах:

Python

epm = []
for u1 in range(1, 20):
    p_row = []
    #print(u1, end=', ')
    for u2 in range(1, 20):
        p_row.append(e_profit_lin([1.1, 1.2, 1.3], [u1, u2, 40], 1000))
    epm.append(p_row)
    
epm = pd.DataFrame(epm, columns=range(1, 20), index=range(1, 20))
plt.figure(figsize=(12, 7))
sns.heatmap(epm, annot=True, fmt=".2f", cmap='nipy_spectral')
plt.ylabel('Subclass D quota')
plt.xlabel('Subclass C quota')
plt.title('Dependence of average profit\non quotas of subclasses D and C');

Светлая область на графике соответствует всем субоптимальным решениям, которые и находит используемый метод оптимизации. Для оптимизации выполняется многократное моделирование процесса продаж и затем вычисляется его среднее значение, которое может испытывать отклонение от истинного матожидания. Почему бы просто сразу не "считать вероятности"? К ответу на этот вопрос мы вернемся ниже, а пока продолжим с построением графика.

Прежде чем взглянуть на то, к чему приводит использование предложенного типа нестинга, давайте воспользуемся немного другими значениями субоптимальных квот — это позволит лучше продемонстрировать их влияние на процесс продаж. Возьмем для подкласса D квоту, равную 7, а для подкласса C — квоту, равную 15. Выглядит как жульничество, но можно выполнить код при других значениях и убедиться, что все верно.

Распределение возможной прибыли по сравнению с предыдущим результатом кардинально поменялось, а ее среднее значение выросло на 1.5%:

Python

X = np.array([1.1, 1.2, 1.3])
Up = np.array([7, 15, 40])
sales_lin = [profit_lin(X, Up) for _ in range(3000)]
sales_lin_df = pd.DataFrame(sales_lin,
                columns=['profit', 'D', 'C', 'J', 'All',
                         'end_t1', 'end_t2', 'end_t3']
               )
#sales_lin_df.head()

sns.histplot(sales_lin_df.profit, binwidth=1)
E_p = sales_lin_df.profit.mean()
plt.axvline(E_p, color='r', label=f'E(Profit) = {E_p:.2f}')
plt.legend()
plt.title('Average profit distribution');

Введение квот также сильно повлияло на распределение количества продаваемых билетов в каждом подклассе (заполняемость):

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_lin_df.D, discrete=True, ax=ax[0])
ax[0].set_title('D (price = 1.1)')
ax[0].set_xlabel('Occupancy')
sns.histplot(sales_lin_df.C, discrete=True, ax=ax[1])
ax[1].set_title('C (price = 1.2)')
ax[1].set_xlabel('Occupancy')
sns.histplot(sales_lin_df.J, discrete=True, ax=ax[2])
ax[2].set_title('J (price = 1.3)')
ax[2].set_xlabel('Occupancy')
plt.tight_layout();

Как видим, введение квот резко ограничивает вариативность, а постепенное уменьшение квоты C до вычисленного выше значения, равного 11, приведет к сдвигу распределения заполняемости подкласса J вправо и уменьшению его правого хвоста.

Самое интересное теперь — это распределение времени окончания продаж авиабилетов:

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_lin_df.end_t1, ax=ax[0])
e_t1 = sales_lin_df.end_t1.mean()
ax[0].axvline(e_t1, color='r', label=f'E(end_t1) = {e_t1:.2f}')
ax[0].legend()
ax[0].set_title('End of period T1 (D sales)')
ax[0].set_xlabel('Day')
sns.histplot(sales_lin_df.end_t2, ax=ax[1])
e_t2 = sales_lin_df.end_t2.mean()
ax[1].axvline(e_t2, color='r', label=f'E(end_t2) = {e_t2:.2f}')
ax[1].legend()
ax[1].set_title('End of period T2 (C sales)')
ax[1].set_xlabel('Day')
sns.histplot(sales_lin_df.end_t3, ax=ax[2])
e_t3 = sales_lin_df.end_t3.mean()
ax[2].axvline(e_t3, color='r', label=f'E(end_t3) = {e_t3:.2f}')
ax[2].legend()
ax[2].set_title('End of period T3 (J sales)')
ax[2].set_xlabel('Day')
plt.tight_layout();

Во-первых, следует обратить внимание на время завершения периода $T_{1}$ — из-за введения квоты он теперь часто заканчивается намного раньше чем за 3 дня до вылета. То же самое можно сказать и о периоде $T_{2}$ . Важно отметить, что время завершения продаж теперь сильно сместилось к времени вылета, а билеты присутствуют в продаже гораздо дольше.

Можно сделать вывод о том, что использование нестинга положительно повлияло как на среднюю прибыль, так и на сам процесс продаж. Тем не менее, несмотря на то, что имеется всего три подкласса, можно попробовать использовать другой тип нестинга и выяснить, как он повлияет на результат. Пусть все остатки мест будут уходить в самый прибыльный подкласс J — такой тип нестинга называется параллельным.

Python

def profit_par(X, Up):
    
    U = np.copy(Up)
    t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
    t = t[t < 10]
    price_idx = betabinom.rvs(n, 1, 0.99 * t + 0.1)
    demand = price[price_idx]

    end_t1 = np.where(t > 3)[0][-1]
    q1_cumsum = np.cumsum(demand[: end_t1 + 1] >= X[0])
    idx_u1 = np.where(q1_cumsum == U[0])[0]
    if idx_u1.size != 0:
        end_t1 = idx_u1[0]
        q1 = q1_cumsum[end_t1]
    else:
        q1 = q1_cumsum[end_t1]

    end_t2 = np.where(t > 1)[0][-1]
    q2_cumsum = np.cumsum(demand[end_t1 + 1 : end_t2 + 1] >= X[1])
    idx_u2 = np.where(q2_cumsum == U[1])[0] + end_t1 + 1
    if idx_u2.size != 0:
        end_t2 = idx_u2[0]
        q2 = q2_cumsum[end_t2 - end_t1 - 1]
    else:
        q2 = q2_cumsum[end_t2 - end_t1 - 1]

    U[2] = 40 - q1 - q2

    q3_cumsum = np.cumsum(demand[np.where(t < t[end_t2])[0]] >= X[2])
    idx_u3 = np.where(q3_cumsum == U[2])[0] + end_t2 + 1
    if idx_u3.size != 0:
        end_t3 = idx_u3[0]
        q3 = q3_cumsum[end_t3 - end_t2 - 1]
    else:
        end_t3 = t.size - 1
        q3 = q3_cumsum[end_t3 - end_t2 - 1]

    profit = q1 * X[0] + q2 * X[1] + q3 * X[2]

    return profit, q1, q2, q3, q1 + q2 + q3, t[end_t1], t[end_t2], t[end_t3]

#X = np.array([1.1, 1.2, 1.3])
#Up = np.array([9, 9, 40])
#profit_par(X, Up)

def e_profit_par(X, Up, n_iter):
    return np.mean([profit_par(X, Up)[0] for _ in range(n_iter)])

def opt_price_vecs(n_iter):
    h_x = np.array([[0.2]*5]*3)
    h_u = np.array([[0.05]*20]*2)
    c_iter = 0
    while h_u.max(axis=1).sum() != 2:
        V_X = np.array([rand_vec_x(h_x) for _ in range(n_iter)])
        V_U = np.array([rand_vec_u(h_u) for _ in range(n_iter)])
        R = np.array([e_profit_par(price[V_X[i_vec]], V_U[i_vec], 200) for i_vec in range(n_iter)])
        idx = np.argsort(R)[::-1][:20]
        h_x = hist_res_x(V_X[idx])
        h_u = hist_res_u(V_U[idx])
        print(np.argmax(h_x, axis=1))
        print(np.argmax(h_u, axis=1))
        print('-'*30)
        c_iter += 1
        if c_iter == 7:
            break
    opt_vec_x = price[np.nonzero(h_x)[1]]
    opt_vec_u = np.hstack((np.argmax(h_u, axis=1), [40]))
    print(opt_vec_x, opt_vec_u)
    return e_profit_par(opt_vec_x, opt_vec_u, 200)

opt_price_vecs(200)

Python

[1 3 3]
[10 11]
------------------------------
[1 2 3]
[17  9]
------------------------------
[1 2 3]
[10  9]
------------------------------
[1 2 3]
[10  9]
------------------------------
[1 2 3]
[10  9]
------------------------------
[1 2 3]
[10  9]
------------------------------
[1 2 3]
[10  9]
------------------------------
[1.1 1.2 1.3] [10  9 40]
48.53200000000001

Оптимальные цены не изменились, но оптимальные квоты приняли другие значения:

D — 10 мест;
C — 9 мест;
J — забирает все оставшиеся места.

Изначально можно ожидать, что значение средней прибыли должно измениться, пускай и не сильно. Тем не менее, этого не произошло — даже форма распределения осталась практически прежней:

Python

X = np.array([1.1, 1.2, 1.3])
Up = np.array([10, 9, 40])
sales_par = [profit_par(X, Up) for _ in range(3000)]
sales_par_df = pd.DataFrame(sales_par,
                columns=['profit', 'D', 'C', 'J', 'All',
                         'end_t1', 'end_t2', 'end_t3']
               )
#sales_par_df.head()

sns.histplot(sales_par_df.profit, binwidth=1)
E_p = sales_par_df.profit.mean()
plt.axvline(E_p, color='r', label=f'E(Profit) = {E_p:.2f}')
plt.legend()
plt.title('Average profit distribution');

На первый взгляд, в заполняемости подклассов нет никаких изменений:

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_par_df.D, discrete=True, ax=ax[0])
ax[0].set_title('D (price = 1.1)')
ax[0].set_xlabel('Occupancy')
sns.histplot(sales_par_df.C, discrete=True, ax=ax[1])
ax[1].set_title('C (price = 1.2)')
ax[1].set_xlabel('Occupancy')
sns.histplot(sales_par_df.J, discrete=True, ax=ax[2])
ax[2].set_title('J (price = 1.3)')
ax[2].set_xlabel('Occupancy')
plt.tight_layout();

Если взглянуть повнимательнее и сравнить полученные данные с предыдущими, то можно заметить, что у распределения заполняемости подкласса C исчез маленький правый хвостик. Связано это с тем, что подкласс D теперь отдает остатки в подкласс J, а не C. Это небольшое, но все же примечательное отличие от предыдущего типа нестинга.

Наиболее важное отличие можно заметить в распределении времени окончания периодов продаж:

Python

f, ax = plt.subplots(1, 3, figsize=(12, 4))

sns.histplot(sales_par_df.end_t1, ax=ax[0])
e_t1 = sales_par_df.end_t1.mean()
ax[0].axvline(e_t1, color='r', label=f'E(end_t1) = {e_t1:.2f}')
ax[0].legend()
ax[0].set_title('End of period T1 (D sales)')
ax[0].set_xlabel('Day')
sns.histplot(sales_par_df.end_t2, ax=ax[1])
e_t2 = sales_par_df.end_t2.mean()
ax[1].axvline(e_t2, color='r', label=f'E(end_t2) = {e_t2:.2f}')
ax[1].legend()
ax[1].set_title('End of period T2 (C sales)')
ax[1].set_xlabel('Day')
sns.histplot(sales_par_df.end_t3, ax=ax[2])
e_t3 = sales_par_df.end_t3.mean()
ax[2].axvline(e_t3, color='r', label=f'E(end_t3) = {e_t3:.2f}')
ax[2].legend()
ax[2].set_title('End of period T3 (J sales)')
ax[2].set_xlabel('Day')
plt.tight_layout();

Время окончания второго периода продаж сильно отдалилось от даты вылета, что объясняется наличием жесткой квоты для подкласса C.

Разумно предположить, что для одного и того же спроса разные типы нестинга могут быть эквивалентными в контексте средней прибыли, но не особенностей самого процесса продаж — два последних примера как раз подтверждают это.

Примеры были взяты крайне простые, а эмерджентность никто не отменял, поэтому пока лучше придерживаться мнения "скорее да", чем "определенно да". На данный момент важность этой гипотезы может показаться сомнительной, но именно она будет являться ключом к оптимизации нестинга.

3. Общая задача оптимизации нестинга

Рассмотренный выше пример прост и создает впечатление, что оптимизировать, собственно, вообще нечего — ведь всего три цены для трех подклассов, три периода и три кривых спроса.

В приведенном выше примере не выполнялся поиск корректирующих цен. Впрочем, он и в самом начале этой статьи выполнялся не совсем корректно — были найдены всего три цены: $\mathrm{Price}_{1}$ , $\mathrm{Price}_{2}$ и $\mathrm{Price}_{3}$ . Каждая из них приводит к некоторой средней прибыли, которая может быть вычислена по простой формуле:

где, как и прежде:

— номер периода;
$q_{i,j}$ — возможные значения спроса в -м периоде;
$P_{i,j}(q_{i,j} | \mathrm{Price}_{i})$ — вероятность значения $q_{i,j}$ при условии, что установлена цена $\mathrm{Price}_{i}$ .

Тогда средняя результирующая прибыль $\mathrm{ResProfit}$ будет равна сумме средних прибылей в каждом периоде:

$E(\mathrm{ResProfit}) = \sum_{i}E(\mathrm{Profit}_{i}) \to \underset{\mathrm{PriceVec}}{\mathrm{max}},$

где $\mathrm{PriceVec}$ — это вектор цен, в котором одна компонента соответствует одному периоду. Такой способ оптимизации $\mathrm{ResProfit}$ выглядит вполне логичным. Единственное ограничение, которое накладывается на данную функцию, связано только с общей емкостью продаваемых мест и тем, что каждое последующее $q_{i+1}$ зависит от предыдущих $q_{i}, q_{i-1},..., q_{1}$ :

Количество продаваемых в каждом периоде билетов не может приводить к превышению емкости. В то же время это ограничение обращает наше внимание на условную зависимость распределения $q_{i+1}$ от предыдущих $q_{i}, q_{i-1},..., q_{1}$ (как минимум это справедливо для последнего периода продаж). Это значит, что выражение для средней прибыли должно выглядеть как:

$E(\mathrm{Profit}_{i}) = \sum_{j}q_{i,j}\mathrm{Price}_{i}P_{i,j}(q_{i,j} | \mathrm{Price}_{i}, q_{i-1},..., q_{1}) \to \underset{\mathrm{Price}}{\mathrm{max}},$

где $P_{i,j}(q_{i,j} | \mathrm{Price}_{i}, q_{i-1},..., q_{1})$ — обозначает вероятность наблюдения величины спроса $q_{i}$ в -м периоде при условии, что установлена цена $\mathrm{Price}_{i}$ и в предыдущих периодах было продано $q_{i-1},..., q_{1}$ билетов соответственно.

Выше оптимизация проводилась путем многократного симулирования процесса продаж, но последнее выражение показывает, что целевая функция может быть получена аналитически:

$E(\mathrm{ResProfit}) = \sum_{k} \left ( \left ( \sum_{i} q_{i}\mathrm{Price}_{i}\right ) P_{k}(\overrightarrow{Q}_{k} | \mathrm{PriceVec}) \right ) \to \underset{\mathrm{PriceVec}}{\mathrm{max}},$

где $\overrightarrow{Q}_{k}$ — это вектор $(q_{i}, q_{i-1}, ..., q_{1})$ , т.е. вектор возможных продаж в каждом периоде, $P_{k}(\overrightarrow{Q}_{k} | \mathrm{Price})$ — вероятность наблюдения такого вектора при выбранных ценах, а — это количество всех возможных векторов, равное:

$k = \prod_{i}j_{i}.$

Сама по себе целевая функция не выглядит монструозной, но вот , которая показывает количество точек в векторном пространстве , может принимать очень большие значения. Это значит, что построение совместного распределения всех возможных значений компонент вектора $(q_{i}, q_{i-1}, ..., q_{1})$ может обернуться невыполнимой задачей в плане вычислений. Собственно, по этой причине и используется эвристическая оптимизация, в которой процесс продаж многократно моделируется — за это приходится платить тем, что находимые решения могут быть субоптимальными. Следует упомянуть, что используемый метод оптимизации с помощью кросс-энтропии крайне гибок, в связи с чем опасения по поводу больших различий между оптимальными и субоптимальными решениями можно отбросить. Полученная целевая функция пригодна для поиска оптимальных цен в каждом из периодов.

Займемся оптимизацией корректирующих цен: выше говорилось, что в случае, когда на некотором из этапов (периодов) распределения перестают быть унимодальными, то сама формулировка "корректирующие цены" становится неверной. В данном случае действительно может оказаться так, что неоптимальные решения на первых этапах могут помочь добиться лучших решений на этапах последующих или завершающих. В таком случае "корректирующие цены" подразумевают то, что найденные оптимальные цены для каждого из периодов по вышеприведенной целевой функции таковыми де-факто не являются. Тогда чем на самом деле являются корректирующие цены?

Рассмотрим среднюю прибыль в самом первом периоде продаж:

$E(\mathrm{Profit}_{1}) = \sum_{j}q_{1,j}\cdot\mathrm{Price}^{(1)} \cdot P_{1,j}(q_{1,j} | \mathrm{Price}^{(1)}) \to \underset{\mathrm{Price}}{\mathrm{max}},$

Если , значит, что есть всего 3 возможных исхода и оптимальная корректирующая цена во втором периоде продаж должна быть подобрана для каждого из них. На втором этапе необходимо найти такой вектор $(\mathrm{Price}^{(2)}_{1}, \mathrm{Price}^{(2)}_{2}, \mathrm{Price}^{(2)}_{3})$ при котором средняя результирующая прибыль будет максимальна. Само выражение для средней результирующей прибыли примет намного более сложную форму:

где $E_{1}$ и $E_{2}$ показывают, что матожидания вычисляются по вероятностям возможных отклонений спроса в первом и втором периодах — это только для двух периодов. Для трех периодов получим:

$E(\mathrm{ResProfit}) = E_{1}(\mathrm{Profit}^{(1)}) + E_{1}(E_{2}(\mathrm{Profit}^{(2)}) + E_{2}(E_{3}(\mathrm{Profit}^{(3)})))$

Выглядит вполне безобидно, но все это означает, что для каждого вектора возможных значений спроса необходимо найти наилучшую комбинацию векторов цен — то есть не одного вектора, а некоторого набора векторов, причем для каждого периода длина вектора цен будет равна $j_{i}$ . Затея выглядит совсем безнадежной, если предположить, что возникновение хотя бы бимодальных распределений в одном из периодов возможно и что задача решается "в лоб".

Ради справедливости стоит отметить, что бимодальность все-таки действительно возможна. Например, если в первом периоде возможные отклонения спроса подчиняются распределению Пуассона с $\mu=13$ , а квота $r^{(1)}=16$ , то будет наблюдаться следующее:

Python

mu = 13

xx = np.arange(poisson.ppf(0.01, mu),
               poisson.ppf(0.99, mu))
yy = poisson.pmf(xx, mu)

r = 16
ind_r = np.where(xx == r)[0][0]
pq1 = yy[:ind_r+1]
pq1[-1] = np.sum(yy[ind_r:])
q1 = xx[:ind_r+1]
plt.stem(q1, pq1)
plt.xlabel(r'$q_{1}$')
plt.ylabel('Probability')
plt.title(r'Distribution of $q_{1}$ with a $r_{1} = 16$');

Есть большие сомнения по поводу того, что лучшая цена во втором и последующих периодах может быть только одной, а остальные корректирующими. В данном случае достаточно провести поиск лучших цен всего для двух случаев: для $q_{(1)} = 16$ и для остальной части распределения возможных значений $q_{(1)}$ . Прибегать к многоэтапному стохастическому программированию нет никакой необходимости, и для каждого из двух случаев можно по-прежнему принять, что есть лучшие и корректирующие цены.

Сама фраза "планирование продаж", также как и "корректирующие цены" легко может сбить с толку: по сути планировать цены на весь период продаж приходится только потому, что продается ограниченное количество билетов. Если нет прогноза на весь или оставшийся период продаж, то подобрать наилучшие цены не получится вообще. Однако это не значит, что необходимо искать решения для абсолютно всех возможных комбинаций отклонений в отдельных подпериодах.

Шум может приводить к так называемой невязке — различию между тем, что ожидалось и тем, что наблюдается. Задача состоит в том, чтобы учитывать такие невязки только по мере их появления, но обязательно с учетом имеющегося прогноза. Фраза "корректирующая цена" (или "корректирующий план") как раз и означает действие, которое направлено на то, чтобы компенсировать наблюдаемую невязку. "Планирование продаж" означает, что нужно планировать цены с учетом всех возможных отклонений спроса, но не всех возможных невязок.

Вышесказанное звучит вполне логично, но имеет свои нюансы. Квоты позволяют задать жесткое ограничение, т.е. ограничить количество продаваемых билетов некоторым числом. Цены при этом можно рассматривать как слабое ограничение — ведь если есть опасения продать большое количество билетов по дешевой цене, то можно просто увеличить цену. В этом случае ограничение будет вероятностным. Что будет, если попробовать совместить жесткие и слабые ограничения?

Предположим, что есть два подпериода продаж, и во втором из них кривая спроса выше, чем в первом. В первом периоде можно установить ограничение с помощью довольно высокой цены. С одной стороны, это плохо — ведь если спрос будет падать, то будет продано мало билетов. Спрос при этом может отклониться и вверх. Если такое отклонение окажется невыгодным (такое может быть, поскольку во втором периоде спрос тоже может увеличиться), то тогда необходимо установить квоту.

Конечно, в случае двух периодов риск прогадать довольно велик. Если периодов больше, то он будет становиться меньше. Если в каком-то периоде спрос отклонится вниз, то появившийся остаток достаточно отдать в тот период, где кривая спроса выше и в котором он может быть исчерпан. Именно нестинг лучше всего подходит для такой стратегии.

Чтобы разобраться с нестингом, необходимо большее количество подклассов — пусть теперь их будет пять, например: J, C, D, I, Z. Если проранжировать все подклассы от самого дорогого — J к самому дешевому — Z, то иерархия подклассов может выглядеть так:

Данная схема показывает, как будут перераспределяться остатки мест и как будет выполняться оптимизация. Если у подкласса нет дочерних подклассов, то количество доступных мест в нем может быть ограничено ценой и/или жесткой квотой. Если же у подкласса есть дочерние подклассы, то количество доступных мест в нем может ограничиваться ценой, жесткой квотой и случайным количеством мест в нижестоящих подклассах. Очевидно — чем больше у подкласса дочерних подклассов, тем больше может быть разброс количества доступных мест для него. Например, у подкласса J в параллельной иерархии разброс количества доступных мест будет больше, чем в комбинированной иерархии, а самый маленький разброс будет в линейной иерархии. Общее количество доступных мест и количество подклассов может быть велико, поэтому, чтобы предотвратить рост дисперсии количества доступных мест по мере продвижения от самых дешевых подклассов к самым дорогим, можно даже прибегнуть к разбиению иерархии на отдельные блоки.

Поскольку какие-то цены могут быть не использованы вовсе, значит, что квоты соответствующих подклассов вообще не будут использованы. В данном случае нужно применять какие-то правила перерасчета мест и всего этих правил — три:

Top-Down — используется по умолчанию, забронированные места подклассов высчитываются из квоты нижестоящего по структуре подкласса, где есть места;
Up-Sell — забронированные места в подклассе высчитываются из квоты самого нижнего в структуре подкласса, в котором есть места ("жадный");
Bottom-Up — забронированные места в подклассе высчитываются из квоты этого подкласса, в котором происходит бронирование, а при превышении квоты высчитываются из самого нижнего в структуре подкласса, в котором есть свободные места.

Задача состоит в том, чтобы найти такую иерархию подклассов и алгоритм перерасчета, при которых случайные и фиксированные количества доступных мест в подклассах будут наилучшим образом соотноситься со случайными отклонениями спроса в них.

Нестинг — это система ограничений для уже знакомой целевой функции.

$E(\mathrm{ResProfit}) = \sum_{k} \left ( \left ( \sum_{i} q_{i}\mathrm{Price}_{i}\right ) P_{k}(\overrightarrow{Q}_{k} | \mathrm{PriceVec}) \right ) \to \underset{\mathrm{PriceVec}}{\mathrm{max}}.$

Пусть $\overrightarrow{R}_{i} = (r_{1}^{(J)}, r_{1}^{(C)}, r_{1}^{(D)}, r_{1}^{(I)}, r_{1}^{(Z)})$ — это вектор квот, причем речь будет идти о квотах, только если . Если , то речь будет идти уже о количестве доступных мест в каждом подклассе в -м периоде продаж.

Если принять иерархию подклассов одной на рисунке выше комбинированной, а в качестве правила перерасчета выбрать правило Up-Sell, то можно составить систему ограничений, которые должны учитываться в каждом периоде продаж. Например, для подкласса D будет работать следующее ограничение:

$(q_{i}^{(D)}, r_{i}^{(D)}) = \begin{cases} (q_{i}^{(D)}, r_{i}^{(D)} - q_{i}^{(D)}), & \text{ if } q_{i}^{(D)} < r_{i}^{(D)} \\ (r_{i}^{(D)}, 0), & \text{ if } q_{i}^{(D)} \geqslant r_{i}^{(D)} \end{cases}$

Это ограничение показывает, что цена подкласса D может использоваться неоднократно, но при этом количество проданных билетов по данной цене не может превышать квоту или количество доступных мест в данном подклассе.

Если используется цена подкласса C, то количество проданных билетов по данной цене будет определяться следующим ограничением:

$(q_{i}^{(C)}, r_{i}^{(C)}, r_{i}^{(D)}) = \begin{cases} (q_{i}^{(C)}, r_{i}^{(C)}, r_{i}^{(D)} - q_{i}^{(C)}), & \text{ if } q_{i}^{(C)} < r_{i}^{(D)} \\ (q_{i}^{(C)}, r_{i}^{(C)} + r_{i}^{(D)} - q_{i}^{(C)}, 0), & \text{ if } r_{i}^{(C)} + r_{i}^{(D)} > q_{i}^{(C)} \geqslant r_{i}^{(D)} \\ (r_{i}^{(C)} + r_{i}^{(D)}, 0, 0), & \text{ if } r_{i}^{(C)} + r_{i}^{(D)} < q_{i}^{(C)} \end{cases}$

Эта система ограничений показывает, что продажи билетов подкласса C теперь приводят к перерасчету количества мест в подклассах C и D. Определяется это правилом Up-Sell — сначала вычитаются места из подкласса D, а в случае, если их не хватает, то затем вычитаются из подкласса C.

Аналогичным образом определяются ограничения для подклассов Z и I:

$(q_{i}^{(Z)}, r_{i}^{(Z)}) = \begin{cases} (q_{i}^{(Z)}, r_{i}^{(Z)} - q_{i}^{(Z)}), & \text{ if } q_{i}^{(Z)} < r_{i}^{(Z)} \\ (r_{i}^{(Z)}, 0), & \text{ if } q_{i}^{(Z)} >= r_{i}^{(Z)} \end{cases}$ $(q_{i}^{(I)}, r_{i}^{(I)}, r_{i}^{(Z)}) = \begin{cases} (q_{i}^{(I)}, r_{i}^{(I)}, r_{i}^{(Z)} - q_{i}^{(I)}), & \text{ if } q_{i}^{(I)} < r_{i}^{(Z)} \\ (q_{i}^{(I)}, r_{i}^{(I)} + r_{i}^{(Z)} - q_{i}^{(I)}, 0), & \text{ if } r_{i}^{(I)} + r_{i}^{(Z)} > q_{i}^{(I)} > r_{i}^{(Z)} \\ (r_{i}^{(I)} + r_{i}^{(Z)}, 0, 0), & \text{ if } r_{i}^{(I)} + r_{i}^{(Z)} < q_{i}^{(I)} \end{cases}$

Поскольку подкласс J находится в самом верху иерархии, то продажи билетов по цене данного подкласса могут приводить к перерасчету мест во всех нижестоящих подклассах:

Можно предположить, что для разных параметров спроса лучшим будет тот или иной тип нестинга. Однако проверка этого предположения потребует большого объема вычислений. Вместо этого попробуем убедиться в том, что результат будет зависеть от величины разброса количества доступных мест. Для этого сначала сравним параллельную и комбинированную иерархию, каждая из которых будет использована с правилом Up-Sell и уже затем сравним эти результаты с динамическим ценообразованием, в котором не используется нестинг, но учитывается и компенсируется с помощью цены любая наблюдаемая невязка. Поскольку подклассов теперь стало 5, то количество подпериодов продаж увеличим до 5, а количество цен из доступного интервала до 9: [1.00, 1.05, 1.10, 1.15, 1.20, 1.25, 1.30, 1.35, 1.40].

Предположим, что прогноз спроса выглядит следующим образом:

Python

price = np.round(np.linspace(1, 1.4, 9), 2)
MU = []
T = [[10, 4], [4, 2.5], [2.5, 1.5], [1.5, 0.5], [0.5, 0]]

for i in range(len(T)):
    mu = []
    for j in range(len(price)):
        dem = []
        for _ in range(1000):
            t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
            t = t[t < 10]
            price_idx = betabinom.rvs(8, 1, 0.99 * t + 0.1)
            demand = price[price_idx]
            if len(np.where(t > T[i][0])[0]) != 0:
                start_t = np.where(t > T[i][0])[0][-1]
            else:
                start_t = 0
            end_t = np.where(t > T[i][1])[0][-1]
            dem.append(np.sum(demand[start_t : end_t + 1] >= price[j]))
        mu.append(np.mean(dem))
    MU.append(mu)
MU = np.array(MU)

plt.plot(price, MU[0], 'o-', label=r'$T_{1}$')
plt.plot(price, MU[1], 'o-', label=r'$T_{2}$')
plt.plot(price, MU[2], 'o-', label=r'$T_{3}$')
plt.plot(price, MU[3], 'o-', label=r'$T_{4}$')
plt.plot(price, MU[4], 'o-', label=r'$T_{5}$')
plt.legend()
plt.xlabel('Price')
plt.ylabel('Mean demand')
plt.title('Demand curves');

Теперь создадим ряд функций и скриптов, необходимых для выполнения оптимизации:

Python

# Функция моделирующая продажи при комбинированном нестинге:
def profit(ps, Up):
    U = np.copy(Up)
    Z, I, D, C, J = np.argsort(ps)

    #print(U)
    #print('-'*30)

    # Z
    q1 = poisson.rvs(MU[0][ps[0]])
    #print('q1 = ', q1)
    if q1 < U[Z]:
        U[Z] = U[Z] - q1
    else:
        q1 = U[Z]
        U[Z] = 0
    #print('q1 =', q1, '; U =', U)
    #print('-'*30)

    # I
    q2 = poisson.rvs(MU[1][ps[1]])
    #print('q2 = ', q2)
    if q2 < U[Z]:
        U[Z] = U[Z] - q2
    elif U[Z] <= q2 < U[Z] + U[I]:
        U[I] = U[Z] + U[I] - q2
        U[Z] = 0
    else:
        q2 = U[Z] + U[I]
        U[Z] = 0
        U[I] = 0
    #print('q2 =', q2, '; U =', U)
    #print('-'*30)

    # D
    q3 = poisson.rvs(MU[2][ps[2]])
    #print('q3 = ', q3)
    if q3 < U[D]:
        U[D] = U[D] - q3
    else:
        q3 = U[D]
        U[D] = 0
    #print('q3 =', q3, '; U =', U)
    #print('-'*30)

    # C

    q4 = poisson.rvs(MU[3][ps[3]])
    #print('q4 = ', q4)
    if q4 < U[D]:
        U[D] = U[D] - q4
    elif U[D] <= q4 < U[D] + U[C]:
        U[C] = U[D] + U[C] - q4
        U[D] = 0
    else:
        q4 = U[D] + U[C]
        U[D] = 0
        U[C] = 0
    #print('q4 =', q4, '; U =', U)
    #print('-'*30)

    # J

    q5 = poisson.rvs(MU[4][ps[4]])
    #print('q5 = ', q5)
    if q5 < U[Z]:
        U[Z] = U[Z] - q5
    elif U[Z] <= q5 < U[Z] + U[I]:
        U[I] = U[Z] + U[I] - q5
        U[Z] = 0
    elif U[Z] + U[I] <= q5 < U[Z] + U[I] + U[D]:
        U[D] = U[Z] + U[I] + U[D] - q5
        U[I] = 0
        U[Z] = 0
    elif U[Z] + U[I] + U[D] <= q5 < U[Z] + U[I] + U[D] + U[C]:
        U[C] = U[Z] + U[I] + U[D] + U[C] - q5
        U[D] = 0
        U[I] = 0
        U[Z] = 0
    elif U[Z] + U[I] + U[D] + U[C] <= q5 < U[Z] + U[I] + U[D] + U[C] + U[J]:
        U[J] = U[Z] + U[I] + U[D] + U[C] + U[J] - q5
        U[C] = 0
        U[D] = 0
        U[I] = 0
        U[Z] = 0
    else:
        q5 = U[Z] + U[I] + U[D] + U[C] + U[J]
        U = np.zeros(5, dtype=int)
    #print('q5 =', q5, '; U =', U)
    #print('-'*30)

    vec_q = np.array([q1, q2, q3, q4, q5])
    profit = np.sum(vec_q * price[ps])
    #print('profit =', profit)
    
    return profit, vec_q, U

# Функция моделирующая продажи при параллельном нестинге
def profit(ps, Up):

    U = np.copy(Up)
    Z, I, D, C, J = np.argsort(ps)
    #print(U)
    #print('-'*30)

    # Z
    q1 = poisson.rvs(MU[0][ps[0]])
    #print('q1 = ', q1)
    if q1 < U[Z]:
        U[Z] = U[Z] - q1
    else:
        q1 = U[Z]
        U[Z] = 0
    #print('q1 =', q1, '; U =', U)
    #print('-'*30)

    # I
    q2 = poisson.rvs(MU[1][ps[1]])
    #print('q2 = ', q2)
    if q2 < U[I]:
        U[I] = U[I] - q2
    else:
        q2 = U[I]
        U[I] = 0
    #print('q2 =', q2, '; U =', U)
    #print('-'*30)

    # D
    q3 = poisson.rvs(MU[2][ps[2]])
    #print('q3 = ', q3)
    if q3 < U[D]:
        U[D] = U[D] - q3
    else:
        q3 = U[D]
        U[D] = 0
    #print('q3 =', q3, '; U =', U)
    #print('-'*30)

    # C

    q4 = poisson.rvs(MU[3][ps[3]])
    #print('q4 = ', q4)
    if q4 < U[C]:
        U[C] = U[C] - q4
    else:
        q4 = U[C]
        U[C] = 0
    #print('q4 =', q4, '; U =', U)
    #print('-'*30)

    # J

    q5 = poisson.rvs(MU[4][ps[4]])
    #print('q5 = ', q5)
    if q5 < U[Z]:
        U[Z] = U[Z] - q5
    elif U[Z] <= q5 < U[Z] + U[I]:
        U[I] = U[Z] + U[I] - q5
        U[Z] = 0
    elif U[Z] + U[I] <= q5 < U[Z] + U[I] + U[D]:
        U[D] = U[Z] + U[I] + U[D] - q5
        U[I] = 0
        U[Z] = 0
    elif U[Z] + U[I] + U[D] <= q5 < U[Z] + U[I] + U[D] + U[C]:
        U[C] = U[Z] + U[I] + U[D] + U[C] - q5
        U[D] = 0
        U[I] = 0
        U[Z] = 0
    elif U[Z] + U[I] + U[D] + U[C] <= q5 < U[Z] + U[I] + U[D] + U[C] + U[J]:
        U[J] = U[Z] + U[I] + U[D] + U[C] + U[J] - q5
        U[C] = 0
        U[D] = 0
        U[I] = 0
        U[Z] = 0
    else:
        q5 = U[Z] + U[I] + U[D] + U[C] + U[J]
        U = np.zeros(5, dtype=int)
    #print('q5 =', q5, '; U =', U)
    #print('-'*30)

    vec_q = np.array([q1, q2, q3, q4, q5])
    profit = np.sum(vec_q * price[ps])
    #print('profit =', profit)
    
    return profit, vec_q, U

# Функция вычисляющая среднюю прибыль:
def e_profit(ps, Up, n_iter):
    return np.mean([profit(ps, Up)[0] for _ in range(n_iter)])

# Софтмакс Тейлора
def tsm(z):
    numerator = 1 + z + 0.5*z**2# + (1/6)*z**3
    denominator = np.sum(1 + z + 0.5*z**2) # + (1/6)*z**3
    return numerator / denominator

# Функция, вычисляющая вероятностное распределение цен
# по выборке наилучших кандидатов:
def hist_ps(res_vals):
    bins = np.r_[0:10]

    h = np.array([tsm(np.histogram(res_vals.T[col],
                               bins=bins)[0])    #, density=True
                  for col in range(5)])
    
    return h

# Функция генерирующая вектор цен на основе 
# заданного распределения:
def rand_ps(h):
    indices = np.r_[0:9]
    vec = [np.random.choice(indices,
                            size=1,
                            p=h_i)[0]
           for h_i in h]
    return vec

# Функция вычисляющая вероятностное распределение
# разбиений количества мест по подклассам:
def hist_up(res_vals):
    bins = np.r_[0:42]
    h = np.array([tsm(np.histogram(res_vals.T[col],
                               bins=bins)[0])    # , density=True
                  for col in range(4)])
    return h

# Функция генерирующая вектор разбиений на основе 
# заданного распределения:
def rand_up(h):
    indices = np.r_[0:41]
    vec = [np.random.choice(indices,
                            size=1,
                            p=h_i)[0]
           for h_i in h]
    return vec

# Функция, вычисляющая количество мест в каждом подклассе
# на основе полученных разбиений:
def calc_up(rand_vec_up):
    vec_up = np.diff(np.sort(np.hstack((rand_vec_up, 0, 40))))
    return vec_up

# Скрипт выполняющий оптимизацию:
'''
for _ in range(5):
    h_ps = np.array([[1/9]*9]*5)
    h_up = np.array([[1/41]*41]*4)

    flag_ps = np.all(np.max(h_ps, axis=1) >= 0.98)
    flag_up = np.all(np.max(h_up, axis=1) >= 0.98)
    while not(flag_ps and flag_up):
        ps_vecs = np.array([rand_ps(h_ps) for _ in range(3000)])
        up_vecs = np.array([rand_up(h_up) for _ in range(3000)])
        R = np.array([e_profit(ps_vecs[i], calc_up(up_vecs[i]), 20) for i in range(3000)])
        idx = np.argsort(R)[::-1][:300]
        h_ps = hist_ps(ps_vecs[idx])
        h_up = hist_up(up_vecs[idx])
        print('price_vec =', price[np.argmax(h_ps, axis=1)], '; quotas_vec = ', calc_up(np.argmax(h_up, axis=1)))
        flag_ps = np.all(np.max(h_ps, axis=1) >= 0.98)
        flag_up = np.all(np.max(h_up, axis=1) >= 0.98)
    print('-' * 100)
    print(np.argmax(h_ps, axis=1), calc_up(np.argmax(h_up, axis=1)))
    print(e_profit(np.argmax(h_ps, axis=1), calc_up(np.argmax(h_up, axis=1)), 5000))
    print('=' * 100)
''';

################################################################
################################################################

# Код для оптимизации динамического ценообразования и модлирования
# продаж с компенсацией наблюдаемой невязки

# Функция, вычисляющая вероятностное распределение цен
# по выборке наилучших кандидатов для произвольного
# количества оставшихся периодов:
def hist_ps(res_vals):
    cols = res_vals.T
    bins = np.r_[0:10]

    h = np.array([tsm(np.histogram(cols[col],
                               bins=bins)[0])
                  for col in range(len(cols))])
    return h

# Функция генерирующая вектор цен на основе 
# заданного распределения:
def rand_ps(h):
    indices = np.r_[0:9]
    
    vec = [np.random.choice(indices,
                            size=1,
                            p=h_i)[0]
           for h_i in h]
    return vec

# Функция генерирующая вектор разбиений на основе 
# заданного распределения для произвольного
# количества оставшихся периодов:
def hist_up(res_vals, seats, num_T):
    bins = np.r_[0 : seats + 2]
    if num_T != 1:
        cols = res_vals.T
        h = np.array([tsm(np.histogram(cols[col],
                                       bins=bins)[0])
                      for col in range(num_T - 1)])
    else:
        h = tsm(np.histogram(res_vals, bins=bins)[0])
    return h

# Функция генерирующая вектор разбиений на основе 
# заданного распределения:
def rand_up(h, seats, num_T):
    indices = np.r_[0: seats + 1]
    if num_T != 1:
        vec = [np.random.choice(indices,
                                size=1,
                                p=h_i)[0]
               for h_i in h]
    else:
        vec = np.random.choice(indices,
                                size=1,
                                p=h)[0]
    return vec

# Функция, вычисляющая количество мест в каждом подклассе
# на основе полученных разбиений:
def calc_up(rand_vec_up, seats, num_T):
    if num_T != 1:
        vec_up = np.diff(np.sort(np.hstack((rand_vec_up, 0, seats))))
        return vec_up
    else:
        return [rand_vec_up]
    
# Функция вычисляющая среднюю прибыль для произвольного
# количества оставшихся периодов::
def profit(ps, Up):
    U = np.copy(Up)
    L = len(ps)
    mu_tmp = MU[-L:]
    #print('U_pre =', U)
    vec_q = np.asarray(poisson.rvs(mu_tmp[np.r_[:L], ps]))
    #print('q_pre =', vec_q)
    if L != 1:
        vec_q[vec_q > U] = U[vec_q > U]
        #print('q_post =', vec_q)
        U = U - vec_q
        #print('U_post =', U)
    else:
        if vec_q < U[0]:
            U[0] = U[0] - vec_q
        else:
            vec_q =U[0]
            U[0] = 0
        #print('q_post =', vec_q)
        #print('U_post =', U)
    
    profit = np.sum(vec_q * price[ps])
    #print('profit =', profit)
    
    return profit, vec_q, U

# Скрипт моделирующий продажи с динамическим ценнобразованием:
'''
def opt_s(seats, num_T):
    h_ps = np.array([[1/9]*9]*num_T)
    if num_T != 1:
        h_up = np.array([[1/(seats + 1)]*(seats + 1)]*(num_T - 1))
    else:
        h_up = np.array([1/(seats + 1)]*(seats + 1))
    if num_T != 1:
        flag_ps = np.all(np.max(h_ps, axis=1) >= 0.98)
        flag_up = np.all(np.max(h_up, axis=1) >= 0.98)
    else:
        flag_ps = np.max(h_ps) >= 0.98
        flag_up = np.max(h_up) >= 0.98

    while not(flag_ps and flag_up):
        ps_vecs = np.array([rand_ps(h_ps) for _ in range(3000)])
        up_vecs = np.array([rand_up(h_up, seats, num_T) for _ in range(3000)])
        R = np.array([e_profit(ps_vecs[i], calc_up(up_vecs[i], seats, num_T), 20) for i in range(3000)])
        idx = np.argsort(R)[::-1][:300]
        h_ps = hist_ps(ps_vecs[idx])
        h_up = hist_up(up_vecs[idx], seats, num_T)
        ps_tmp = price[np.argmax(h_ps, axis=1)]
        if num_T != 1:
            up_tmp = calc_up(np.argmax(h_up, axis=1), seats, num_T)
        else:
            up_tmp = calc_up(np.argmax(h_up), seats, num_T)
        #print('price_vec =', ps_tmp, '; quotas_vec = ', up_tmp)
        if num_T != 1:
            flag_ps = np.all(np.max(h_ps, axis=1) >= 0.98)
            flag_up = np.all(np.max(h_up, axis=1) >= 0.98)
        else:
            flag_ps = np.max(h_ps) >= 0.98
            flag_up = np.max(h_up) >= 0.98
    ps_opt = np.argmax(h_ps, axis=1)
    if num_T != 1:
        up_opt = calc_up(np.argmax(h_up, axis=1), seats, num_T)
    else:
        up_opt = calc_up(np.argmax(h_up), seats, num_T)
    res_ep = e_profit(ps_opt, up_opt, 2000)
    print('res_ep =', res_ep, 'price_vec =', ps_opt, '; quotas_vec = ', up_opt)
    print('-' * 100)
    return res_ep, ps_opt, up_opt
''';

Теперь можно выполнить оценку максимальной средней прибыли для каждого типа продаж:

Python

# Комбинированный нестинг
comb_1 = np.array([48.5 , 48.05, 49.1 , 48.2 , 49.3 , 47.8 , 47.2 , 48.95, 45.6 ,
                  42.05, 47.75, 47.8 , 48.05, 47.65, 48.2 , 48.1 , 49.15, 40.85,
                  48.05, 47.7 ])
comb_2 = np.array([44.25, 48.05, 47.8 , 48.25, 48.15, 47.95, 47.95, 47.8 , 48.  ,
                  48.  , 44.15, 48.45, 47.7 , 44.15, 47.85, 44.3 , 44.55, 48.1 ,
                  44.25, 48.05])
comb_3 = np.array([47.4 , 47.4 , 47.55, 47.3 , 47.45, 47.75, 47.55, 47.45, 47.5 ,
                  47.6 , 47.35, 47.35, 47.45, 47.55, 42.75, 47.5 , 47.4 , 42.75,
                  47.9 , 47.55])
comb_4 = np.array([47.1, 46.6, 47.2, 46.6, 47.8, 41.9, 47.2, 46.6, 47.8, 46.8, 47.5,
                  48. , 47.1, 47.7, 47.5, 47.7, 46.7, 47.7, 48.7, 47.2])
comb_5 = np.array([47.7 , 48.45, 47.45, 48.15, 48.25, 48.3 , 47.5 , 47.3 , 34.4 ,
                  47.3 , 49.  , 46.45, 46.95, 48.4 , 47.8 , 42.55, 47.85, 41.85,
                  48.55, 47.5])
comb = np.hstack((comb_1, comb_2, comb_3, comb_4, comb_5))


## Параллельный нестинг
par_1 = np.array([46.65, 47.3 , 45.  , 47.15, 47.3 , 39.7 , 46.2 , 46.8 , 46.65,
                  46.8 , 45.65, 47.2 , 47.2 , 47.6 , 47.55, 46.85, 46.6 , 46.65,
                  39.85, 47.  ])
par_2 = np.array([46.3 , 47.45, 47.25, 46.15, 47.4 , 47.1 , 44.15, 46.15, 44.95,
                  47.2 , 43.55, 47.35, 47.05, 47.25, 47.4 , 47.5 , 47.45, 47.45,
                  46.1 , 42.3 ])
par_3 = np.array([40.3 , 43.75, 48.  , 47.7 , 47.8 , 46.6 , 48.15, 47.6 , 47.8 ,
                  45.4 , 46.5 , 47.5 , 47.4 , 47.4 , 43.85, 47.8 , 48.4 , 48.  ,
                  47.6 , 47.4 ])
par_4 = np.array([47.9 , 47.95, 47.15, 47.95, 47.9 , 45.95, 48.05, 47.55, 42.05,
                  44.35, 41.95, 43.35, 48.35, 47.85, 47.85, 48.3 , 40.75, 48.3 ,
                  48.05, 47.65])
par_5 = np.array([46.1 , 40.05, 47.35, 43.6 , 47.35, 46.1 , 47.35, 47.35, 47.55,
                  45.65, 47.35, 41.3 , 47.35, 47.35, 47.35, 47.35, 47.35, 43.35,
                  47.35, 47.35])
par = np.hstack((par_1, par_2, par_3, par_4, par_5))


## Динамическое ценообразование без нестинга

dyn = np.array([46.8, 47.4, 46.95, 46.45, 46.8, 41.2, 46.4, 46.75, 46.5, 46.8,
                47.25, 46.2, 46.95, 46.6, 46.65, 38.7, 42.9, 46.7, 46.75, 46.9])

# Бутстрап:

comb_var_e = [np.mean(comb[np.random.randint(0, comb.size, size=20)]) for _ in range(1000)]
par_var_e = [np.mean(par[np.random.randint(0, par.size, size=20)]) for _ in range(1000)]
dyn_var_e = [np.mean(dyn[np.random.randint(0, dyn.size, size=20)]) for _ in range(1000)]


sns.kdeplot(comb_var_e, c='b', label='Combined')
plt.axvline(np.mean(comb_var_e), c='b', ls=':')
sns.kdeplot(par_var_e, c='r', label='Parallel')
plt.axvline(np.mean(par_var_e), c='r', ls=':')
sns.kdeplot(dyn_var_e, c='g', label='Dynamic Pricing')
plt.axvline(np.mean(dyn_var_e), c='g', ls=':')
plt.legend()
plt.title('Estimation of maximum average profit');

Как видим, гипотеза подтвердилась — комбинированная иерархия позволила добиться гораздо лучшего результата. Удивительно здесь совсем другое — динамическое ценообразование с компенсацией невязки оказалось далеко позади. Оказывается, что компенсирование невязки, наблюдаемой после окончания каждого из подпериодов, с помощью изменения цены намного проигрывает фиксированной стратегии в которой случайные количества доступных к продаже мест наилучшим образом соотносятся со случайными отклонениями спроса.

К слову, компенсация невязки — это как раз то, что пытается сделать человек, продающий билеты. Очевидно, что человеку крайне сложно просчитать данную компенсацию с учетом всех прогнозов — он делает это заведомо хуже, чем алгоритм динамического ценообразования с компенсацией невязок, и гораздо хуже, чем стратегия с применением нестинга. Какими могут быть потери прибыли? Различие между худшим и лучшим результатом на вышеприведенном графике составляет порядка 2%. В реальности потери могут запросто доходить до 30%, а среднее значение будет порядка 15-20%.

Оценка таких потерь кажется очень неправдоподобной, но тут важно учесть, что не в каждой авиакомпании есть сильный отдел DS. Более того, не каждая компания пользуется RMS — а если и пользуется, то зачастую только в рекомендательном режиме, оставляя конечное решение по выбору цены за человеком. Далее стоит заметить, что RMS сами по себе — это кот в мешке, поскольку нет никаких сравнений на открытых данных: ни соревнований, ни чемпионатов, которые позволяли бы проранжировать производителей и их RMS.

Можем попробовать сравнить результаты для других параметров спроса. Допустим, что теперь спрос увеличивается ближе к середине и падает по мере приближения даты вылета:

Python

xd = np.array([0.1, 1.0, 2.0, 4.0, 6.0,  8.0,  9.5, 9.9])
yd = np.array([0.6, 0.6, 0.6, 9.9, 7.1, 0.8, 0.5, 0.5])
z = np.polyfit(xd, yd, 10)
p = np.poly1d(z)

MU = []
T = [[10, 4], [4, 2.5], [2.5, 1.5], [1.5, 0.5], [0.5, 0]]

for i in range(len(T)):
    mu = []
    for j in range(len(price)):
        dem = []
        for _ in range(1000):
            t = np.sort(gamma.rvs(a=0.9, scale=3, size=100))[::-1]
            t = t[t < 10]
            price_idx = betabinom.rvs(8, 1, p(t))
            demand = price[price_idx]
            if len(np.where(t > T[i][0])[0]) != 0:
                start_t = np.where(t > T[i][0])[0][-1]
            else:
                start_t = 0
            end_t = np.where(t > T[i][1])[0][-1]
            dem.append(np.sum(demand[start_t : end_t + 1] >= price[j]))
        mu.append(np.mean(dem))
    MU.append(mu)
MU = np.array(MU)

plt.plot(price, MU[0], 'o-', label=r'$T_{1}$')
plt.plot(price, MU[1], 'o-', label=r'$T_{2}$')
plt.plot(price, MU[2], 'o-', label=r'$T_{3}$')
plt.plot(price, MU[3], 'o-', label=r'$T_{4}$')
plt.plot(price, MU[4], 'o-', label=r'$T_{5}$')
plt.legend()
plt.xlabel('Price')
plt.ylabel('Mean demand')
plt.title('Demand curves');

Результаты предсказуемы, но различия уже не такие сильные:

Python

comb_1 = np.array([49.65, 49.55, 49.45, 49.9 , 49.55, 49.05, 48.6 , 48.4 , 47.9 ,
       49.5 , 48.9 , 48.65, 48.15, 48.1 , 47.75, 49.8 , 48.4 , 48.45,
       49.5 , 49.6])
comb_2 = np.array([49.15, 49.85, 49.55, 44.7 , 50.05, 50.  , 48.05, 49.15, 48.2 ,
       49.25, 45.5 , 49.2 , 49.75, 50.3 , 49.4 , 50.65, 49.2 , 49.9 ,
       49.65, 48.6])
comb_3 = np.array([48.95, 38.4 , 49.1 , 48.35, 36.  , 48.8 , 49.25, 48.75, 48.45,
       48.7 , 49.  , 48.7 , 48.8 , 49.05, 49.35, 48.65, 48.7 , 48.2 ,
       48.45, 48.85])
comb_4 = np.array([48.6 , 48.85, 44.65, 48.75, 49.4 , 49.45, 37.9 , 48.45, 48.4 ,
       46.95, 47.25, 42.  , 48.55, 49.6 , 48.6 , 49.3 , 48.4 , 48.75,
       48.8 , 50.])
comb_5 = np.array([47.25, 48.3 , 47.4 , 47.5 , 47.8 , 48.  , 48.1 , 48.7 , 49.2 ,
       48.6 , 48.8 , 48.7 , 49.3 , 47.7 , 44.55, 49.2 , 48.9 , 48.  ,
       48.  , 48.9])
comb = np.hstack((comb_1, comb_2, comb_3, comb_4, comb_5))



par_1 = np.array([48.8 , 48.2 , 47.75, 48.8 , 49.1 , 47.85, 48.8 , 49.7 , 48.35,
                  46.45, 48.5 , 48.05, 48.  , 48.95, 48.95, 45.6 , 48.65, 49.1 ,
                  49.1 , 47.75])
par_2 = np.array([48.35, 48.95, 47.1 , 47.75, 48.35, 48.35, 48.  , 48.95, 49.1 ,
                  47.75, 48.25, 46.35, 48.35, 49.15, 49.55, 41.65, 48.05, 47.9 ,
                  48.15, 43.65])
par_3 = np.array([47.05, 48.25, 46.85, 46.25, 47.05, 48.05, 47.25, 47.85, 48.05,
                  48.5 , 44.4 , 48.65, 48.45, 48.45, 46.9 , 47.85, 47.65, 48.1 ,
                  48.65, 47.05])
par_4 = np.array([49.65, 49.2 , 48.6 , 49.2 , 46.95, 49.35, 49.25, 47.85, 48.6 ,
                  49.5 , 48.75, 48.75, 48.95, 49.2 , 48.75, 48.15, 48.9 , 48.6 ,
                  49.05, 48.3])
par_5 = np.array([48.45, 49.35, 47.1 , 47.85, 49.35, 48.5 , 48.05, 47.85, 47.55,
                  49.2 , 48.85, 49.05, 48.9 , 48.85, 45.45, 49.35, 47.6 , 48.25,
                  48.1 , 48.3])
par = np.hstack((par_1, par_2, par_3, par_4, par_5))



dyn = np.array([46.8, 47.1, 47.75, 47.5, 47.3, 47.75, 47.45, 47.65, 47.8, 46.85,
                47.85, 47.1, 42.9, 46.7, 47.5, 47.05, 46.95, 45.15, 48.0, 47.4])



# Бутстрап:

comb_var_e = [np.mean(comb[np.random.randint(0, comb.size, size=20)]) for _ in range(1000)]
par_var_e = [np.mean(par[np.random.randint(0, par.size, size=20)]) for _ in range(1000)]
dyn_var_e = [np.mean(dyn[np.random.randint(0, dyn.size, size=20)]) for _ in range(1000)]

sns.kdeplot(comb_var_e, c='b', label='Combined')
plt.axvline(np.mean(comb_var_e), c='b', ls=':')
sns.kdeplot(par_var_e, c='r', label='Parallel')
plt.axvline(np.mean(par_var_e), c='r', ls=':')
sns.kdeplot(dyn_var_e, c='g', label='Dynamic Pricing')
plt.axvline(np.mean(dyn_var_e), c='g', ls=':')
plt.legend()
plt.title('Estimation of maximum average profit');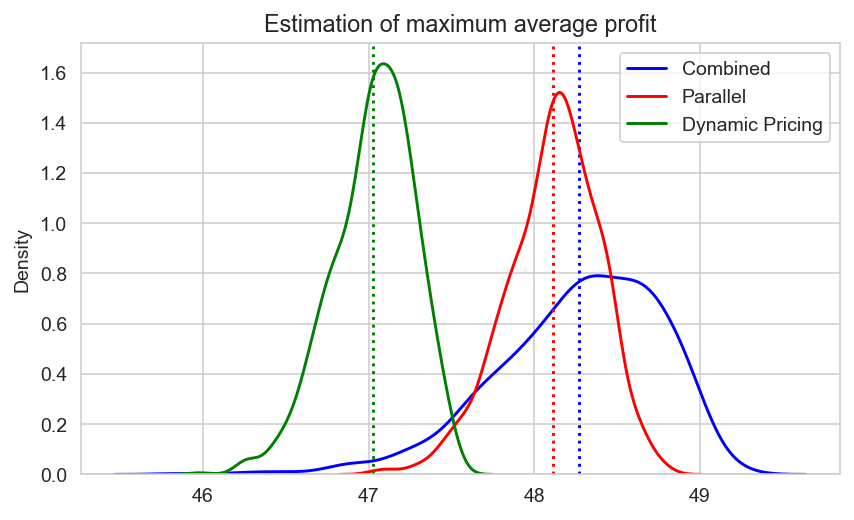

Для спроса с такими параметрами нужно выполнять поиск лучшего типа нестинга, как и при любом серьезном изменении спроса. Как это сделать? Оптимизация методом кросс-энтропии позволяет определять наилучшие цены и квоты для заданного типа нестинга. В крайнем случае, можно выполнить полный перебор всех возможных типов, ведь таких типов не так много, как могло показаться.

Можно ошибочно подумать, что все клонится в сторону топологической оптимизации, так как речь идет о поиске оптимальной структуры иерархии подклассов. Однако иерархия не может быть абсолютно произвольной — как минимум в этой структуре высота подклассов определяется стоимостью билетов в нем. Тип нестинга скорее стоит рассматривать как гиперпараметр, выбор которого ложится на плечи человека, при этом не значит, что все гиперпараметры не могут быть оценены. Можно ввести метрики для типа нестинга, ввести метрики для параметров спроса, а далее произвести оценку их сочетаемости с помощью вероятностного программирования или других методов ML.

Следует рассказать немного подробнее о том, как появился нестинг, чтобы предложенная идея не воспринималась как неотвратимость полного перебора.

До появления нестинга все управление доходами базировалось на гипотезе о "ранней пташке", которая перекочевала в авиацию (!) из ресторанного бизнеса. Иногда клиенты ресторана, дабы не остаться вечером без столика, приходили намного раньше остальных клиентов, из-за чего и стали называться ранними пташками. Разумеется, такое поведение клиентов не устраивало владельцев ресторанов — ведь стол, занятый ранними пташками, могли бы занять более состоятельные клиенты, которым нет надобности заранее планировать поход в ресторан. Такие понятия, как бронирование и резервирование (можно приравнять к квотированию) появились задолго до появления самолетов.

Неудивительного, что гипотеза о ранней пташке перекочевала в представления о спросе на билеты в гражданской авиации, и ее можно подкрепить разными логическими рассуждениями. Например, что срочные командировки не могут быть спланированы заранее и что из-за срочности клиенты готовы платить больше. В то же время семья может спланировать свой отдых гораздо раньше даты вылета, но ей нет необходимости переплачивать за срочность. Очевидно, если первые не могут полностью покрыть мощность предложения, то опыт рестораторов более чем приемлем — достаточно правильным образом постепенно увеличивать стоимость билетов и резервировать какое-то количество мест, для тех, кто готов переплачивать за срочность.

Обоснованные сомнения в гипотезе ранней пташки появились вместе с появлением дальнемагистральных рейсов: оказалось, что некоторые важные поездки планируются заранее. При этом, если не купить билет заранее, возникает риск остаться вовсе без билета. Застраховать риск довольно просто — достаточно купить билет задолго до вылета, пусть и по гораздо большей цене. Если допустить, что подобное поведение свойственно для некоторой части всех пассажиров, то гипотеза крайне сомнительна.

В результате сомнений и появилась первая идея о параллельном нестинге: если спрос увеличивается настолько, что соответствует значениям, близким к дате вылета, то почему бы не увеличивать стоимость билетов и продавать их за счет мест из классов с более низкими ценами? Идея хорошая, но она стала базироваться на другой гипотезе стационарного спроса.

Стационарность — это зашумленный детерминизм, когда в целом все движется так, как прогнозируется, но с небольшими случайными отклонениями. Если вдруг происходят какое-то серьезные отклонения от прогноза, это означает, что после них все снова станет стационарным — значит, что можно пользоваться практически тем же самым прогнозом, от которого недавно произошло отклонение. Однако математическая статистика тоже не стояла на месте, и, как оказалось на практике, тестирование на стационарность не всегда было в пользу последней.

Отсутствие стационарности означает, что жесткое квотирование менее дорогих подклассов — плохая идея, ведь, если прогноз может быть ошибочен, лучше начать продавать билеты по более низкой цене за счет мест из еще более дешевых подклассов. При этом, если спрос двинется вверх, то терять возможность продать большее количество мест по самым высоким ценам тоже не хочется — именно так и появился линейный нестинг. Когда у авиакомпаний появились разные каналы продаж, стало ясно, что простого линейного нестинга недостаточно — так уже появился комбинированный нестинг.

Разумеется, такой исторический экскурс не следует воспринимать буквально, но стоит признать, что в какой-то степени все так и было. Главное, что поиск лучшего типа нестинга может быть построен на вполне разумных субъективных суждениях: знаниях + логике. Если субъективные суждения возникают в условиях неопределенности, то вероятностное программирование становится самым надежным инструментом.

В этой статье, как и в предыдущей, не рассматривались методы создания прогнозных моделей. Данные модели являются регрессионными и могут быть получены с помощью вероятностного программирования. Более того, они могут включать в себя такие данные как: скидки, цены конкурентов и т.д. В будущем планируется подготовка статьи о том, как вероятностное программирование может применяться для создания моделей спроса, а также оценки перспективности того или инного типа нестинга для него.

Нестинг известен давно, при этом попыток его оптимизации вместе с ценами и квотами никогда не предпринималось. Показанный в статье результат был бы невозможен без стохастического програмирования, которое наиболее естественным образом подходит для ситуаций с неопределенностью, и даже он был бы невозможен без оптимизации методом кросс-энтропии. В статье неоднократно говорилось, что этот метод может быть улучшен самыми разными способами, но не говорилось как именно. Можно заметить, что в последнем представленном коде для оптимизации и моделирования появились некоторые необговоренные функции, и одна из них — это софтмакс Тейлора:

$\mathrm{Tsm}(\vec{z})_{i} = \frac{1+z_{i}+0.5z_{i}^{2}}{\sum_{j=1}^{K}(1+z_{j}+0.5z_{j}^{2})},$

где и $\vec{z} = (z_{1}, ..., z_{K}) \in R^{K}$ . Данная функция полезна тем, что позволяет регулировать дискриминацией классов, а в нашем случае дискриминацией отдельных решений. При очень сильной дискриминации алгоритм может придавать больший вес тем решениям, которые показали большое значение средней прибыли лишь из-за случайного отклонения.

Функция софтмакса может быть произвольной, например, такой:

$\mathrm{Sm}(\vec{z})_{i} = \frac{z_{i}^{m}}{\sum_{j=1}^{K}(z_{j}^{m})}.$

Увеличение параметра от итерации к итерации будет приводить к постепенному увеличению дискриминации и способствовать наиболее плавному сужению перспективных областей для поиска решений.

В статье при этом не рассматривалась задача о вероятностных распределениях для случайных разбиений всей доступной емкости по подклассам. В коде представлены необходимые для этого функции, но объяснение всех нюансов, связанных со случайными разбиениями и их совместимостью с концепцией кросс-энтропии, выходит далеко за рамки этой статьи.

Следует также упомянуть, что в стохастическом программировании решением часто становятся не числа, а функционалы — из-за чего разные решения могут приводить к практически неразличимым результатам. Квоты для двух подклассов Z и I могут принимать разные значения: например, 13 и 8 или 10 и 11, но при этом приводить к одинаковым значениям средней прибыли. Однако, если провести моделирование, то эти значения не могут быть абсолютно произвольными, но будут давать в сумме фиксированное количество мест (например, 21).

Динамическое ценообразование для билетов — это не так просто, как можно было изначально подумать. Неожиданным также оказалось то, что нестинг действительно оказался гораздо лучше, чем динамическое ценообразование с компенсацией невязки. В то же время, виновник тому — стохастическое программирование, в котором практически всегда происходит что-то неожиданное.

Заключение

Существует много примеров внедрения RMS различными авиакомпаниями, которое, как правило, всегда приводит к существенному росту прибыли. К заявлениям об увеличении прибыли стоит относиться скептично, ведь никаких стандартизированных или общепринятых метрик для эффекта от внедрения RMS на данный момент до сих пор нет: непонятно учитывается рост или снижение затрат на маркетинг, рост или спад экономики и т.д. В то же время, несмотря на заявления о приросте прибыли, по данным IATA, средняя заполняемость самолетов составляет всего около 70% (а на деле даже 95% — это мало!). Это говорит о том, что планирование продаж и планирование полетов выполняются отдельно. Сложно представить, чтобы управление ценой с учетом расписания приводило к тому, что самолеты все равно могут летать полупустыми, но такое все равно происходит. Следовательно, при моделировании спроса расписание либо не учитывается должным образом, либо не учитывается вовсе — это неизбежно приводит к резким колебаниям цены. Можно ли уменьшить ее волатильность и при этом добиться еще большей эффективности? Ответ — да, это действительно возможно благодаря внедрению современных практик DS, стохастического и вероятностного программирования.

Для руководства любой авиакомпании планирование продаж — это прогнозируемость и понимание ожидаемых показателей, которые дают возможность руководству управлять своими инвестициями, добавлять соответсвующий маркетинг, смещать фокус с ручной подкрутки цен (коммерческим директором или ведущим тарификатором) на работу по улучшению сервиса и качество предоставляемых услуг. Это также позволит заниматься более эффективной оптимизацией операционных процессов: маршрутной сети, расстановки флота и сокращения прочих издержек.

Для конечных потребителей планирование продаж — это прозрачность, предсказуемость и логичность рынка. В настоящее время авиакомпании в большинстве случаев загоняют потребителей в ощущение хаоса, непонимания и несправедливости, что явно снижает желание пользоваться услугами отрасли. И правда, что должен чувствовать путешественник, который видит, что за 30 дней до вылета билет стоит 40 тысяч рублей, затем в течение двух недель цена постепенно растет с небольшими дельтами до 48 тысяч рублей, а потом резко падает до 33 тысяч рублей? Ведь это реальный пример, в котором цена снизилась более чем на 30% и держалась такой в течение нескольких дней — и это не была какая-то рекламная кампания по распродаже.

Такое "ценообразование" встречается сплошь и рядом до сих пор и не вызывает у потребителей ничего, кроме необходимости покупать билеты заранее с услугой возможности возврата средств, чтобы отслеживать дальнейшую стоимость билета и в случае ее падения возвращать билет и покупать новый, оставаясь в выигрыше.

Весь результат статьи можно свести к простой идее: оптимальная цена — это статистически обоснованный консенсус, представляющий собой минимум возражений по поводу цены как со стороны клиента, так и со стороны продавца. Эффективное планирование продаж — это не только про то, что авиакомпании смогут потратить немного денег за более совершенную технологию и заработать еще больше. Главное здесь — это переработка функционирования всей отрасли и взаимоотношений между отраслью и потребителями.

Во всех отраслях e-commerce бьется за user experience (опыт взаимодействия), создавая у пользователей ощущение выгодности предложения или его эксклюзивности. В авиаотрасли этого нет от слова совсем (исключение — распродажи). Для нас неопределенность воспринимается как вероятностные распределения, доверительные интервалы и матожидания. Для простых пассажиров же эта неопределенность — это ощущение безысходности: либо брать так, как есть сейчас, либо черт знает, как будет и будет ли вообще.

Опыт покупки авиабилетов влияет на отношение пассажиров к полетам и действительно способен смещать их предпочтения на другие виды транспорта: жд, автобусы, личное авто. Из-за этого также смещаются предпочтения на локации отдыха: становится проще отдохнуть на даче или в санатории недалеко от родного города, чем слетать за 1500 км на море или горнолыжный курорт. Отказ от таких путешествий прямым и косвенным образом мешает развиваться всей экономике. Логистика — это не просто перемещение из точки А в точку Б, это рациональное использование всех доступных ресурсов, которые повышают эффективность этого перемещения. Именно поэтому логистика является главным драйвером для экономики.

Изменения отношения пассажиров к полетам, включая стоимость билетов, их доступность, а также создание положительного опыта путешественников оказывают глубокий положительный эффект не только на определенную авиакомпанию и ее прибыль, но и на всю экономику в целом — то есть на каждого из нас.

Комментарии (3)

hardtop
16.01.2024 06:35
#26383980
+2
Это шииииикарно! Спасибо за интересную статью с примерами и объяснением.

ptr128
16.01.2024 06:35
#26387662
+2
Цена, вообще-то, тоже немного дискретна. Психологически, 9200 от 9400 отличается меньше, чем 9900 от 10000
1. AndreyKotlov Автор
  16.01.2024 06:35
  #26391436
  Психологическое восприятие цены — это и правда интересный нюанс. В данной статье о нем не сказано, так как в ней рассмотрен упрощенный вариант модели. Реальная модель является полноценной RMS-системой, которая действительно намного сложнее и учитывает множество самых разных факторов, в том числе и социологические. К сожалению, предоставить ее подробное описание в рамках статьи не представляется возможным, так как она уже используется в работе и относится к конфиденциальной информации компании.