Планирование — это сложный процесс, в котором мы сначала создаем образ наилучшего будущего, а затем выполняем поиск наиболее эффективного и удобного для нас пути к его достижению. Однако тенденция такова, что зачастую планы создаются для успокоения. При этом случайности отводится очень важная, но скорее негативная роль — оправдывать то, что оправдывать не следует. Сколько раз вам доводилось слышать, что невозможно учесть все возможные случайные факторы? Или что-то вроде: "Что человек предполагает, а Бог располагает"? Было бы неразумно верить, что любые проблемы, которые может вызывать случайность, возможно решить с помощью прикладной математики. При этом нам все равно необходимо максимально четко понимать роль и влияние случайность в наших планах, чтобы не оправдывать ей потом все наши неудачи.

Проблема интуитивного восприятия вероятности

Когда ничего не подозреваешь о своем незнании, из-за чего некорректно определяешь границ своих компетенций, никогда не возникает ощущения, что ситуация, в которой находишься, на самом деле может быть как минимум странной. Это касается даже самых простых решений, например, банальная арифметика: , если и , то . А что, если и - это случайные величины? Пусть и , где они распределены непрерывно и равномерно. Было бы логично утверждать, что , но это неверно: распределение больше не является равномерным, хоть и заключено в указанных границах.

На графиках представлены распределения двух случайных величин (слева) и распределение их суммы (справа). Если случайные величины реализованы и мы наблюдаем их конкретные значения, то любая арифметика над этими значениями будет работать привычным образом. Однако стоит заговорить о распределениях этих величин, как в дело вступают совсем другие правила.

Как в реальной жизни чаще всего выполняются оптимизация, планирование и принятие решений? Берутся некоторые данные, агрегируются и подставляются в модель. Рассмотрим этот процесс детальнее — допустим, у нас есть 20 наблюдений случайной величины:

# Делаем все необходимые импорты:
import numpy as np
np.random.seed(42)
from scipy import stats
from scipy.stats import norm, binom, bernoulli, poisson, uniform, beta
from scipy.integrate import quad
from scipy import optimize
import matplotlib.pyplot as plt
from pylab import rcParams
rcParams['figure.figsize'] = 10, 6
%config InlineBackend.figure_format = 'png'
import seaborn as sns
sns.set()
import warnings
warnings.filterwarnings('ignore')

values = norm.rvs(10, 2, 20)
sns.kdeplot(data=values, label='kde')
sns.rugplot(data=values, height=.1, label='values')
plt.axvline(values.mean(), c='r', label='mean')
plt.legend()
title = plt.title('''Ядерная оценка плотности и среднее значение
20-ти наблюдений случайной величины''', fontsize=15);

В целевой функции или в системе ограничений окажется именно среднее значение этой величины, при этом факт распределения исходной величины не учтен. Обычно этому есть веское оправдание: появление значений, близких к математическому ожиданию, наиболее вероятно. В связи с этим попадание в глобальный максимум или минимум с захватом допустимой области окажется также наиболее вероятным. Казалось бы, простое и интуитивно понятное объяснение, но так ли это работает на самом деле?

Допустим, случайные величины присутствуют как в целевой функции, так и в системе ограничений. Используя средние значения, мы действительно можем найти минимум или максимум целевой функции, но это будет также означать, что в действительности мы будем отклоняться от оптимального значения, попадая в допустимую область с некоторой вероятностью. Это значит, что мы не можем игнорировать форму результирующих распределений, которая может иметь весьма неожиданный вид. Например, если в целевой функции выполняется сложение двух случайных величин, имеющих равномерное и нормальное распределения, то на анимации ниже можно увидеть, как будет выглядеть их результирующее распределение:

Эти распределения симметричны, но если исходные распределения не являются симметричными, то и результат их суммы вероятнее также не будет симметричным. Это удобно продемонстрировать на сумме двух бета-распределений:

Естественно, одной лишь суммой дело не ограничивается. Вот так будет выглядеть произведение двух равномерно распределенных случайных величин:

Распределение произведения двух величин, распределенных равномерно и нормально, не обязано быть симметричным, и это также наталкивает на мысль о том, что использование математических ожиданий не всегда является решением:

В большей степени это характерно для распределения произведения величин из несимметричных распределений:

Использование математических ожиданий не гарантирует, что что-то иное будет в среднем оптимизировано по такому же принципу. Например, пытаясь минимизировать таким образом средние расходы, нет никаких гарантий, что они действительно будут минимизированы. Зачастую такие действия приводят к отклонениям от вычисленного оптимального значения или выходам из области допустимых значений. Все расхождения затем списываются на случайность и неопределенность, которые никак изначально в модели не учитывались.

Если мы пытаемся минимизировать средние росходы, то разве не было бы правильным хотя бы взглянуть на приблизительную форму распределения расходов? Ведь знание об этой форме представляет собой дополнительную ценную информацию, которая позволяет принимать более взвешенные решения. Такая информация помогает ошибаться, как бы странно это ни звучало.

Абстрактный пример

В качестве базового примера, как случайность постепенно прорывается в наши представления о реальном мире, возьмем простейшую задачу линейного программирования.

Пусть целевая функция имеет следующий вид:

А ее допустимая область ограничивается следующей системой неравенств:

Решение этой задачи не составит труда, поскольку она линейная и детерминированная, что позволяет воспользоваться обычными решателями:

def expr(x):
    return -(27*x[0] + 35*x[1])

def constr_1(x):
    return -1200 + 2*x[0] + 5*x[1]

def constr_2(x):
    return -200 + 0.5*x[0] + 0.25*x[1]

con_1 = {'type': 'eq', 'fun': constr_1}
con_2 = {'type': 'eq', 'fun': constr_2}

cons = (con_1, con_2)

x_0 = np.ones(2)
result = optimize.minimize(expr, x0=x_0, method='SLSQP',
                           constraints=cons)['x']
result

array([350., 100.])

В результате мы получаем оптимальную точку, которая находится на границе допустимой области:

x2 = np.linspace(60, 130, 300)

x11 = 600 - 2.5*x2
x12 = 400 - 0.5*x2

plt.plot(x2[x2>100], x11[x2>100], c='r')
plt.plot(x2[x2<100], x12[x2<100], c='r')
plt.scatter(100, 350, zorder=100, c='r', s=150)
plt.ylabel(r'$x_{1}$', fontsize=15, rotation=0, labelpad=15)
plt.xlabel(r'$x_{2}$', fontsize=15, rotation=0)
plt.title('Графическая интерпретация решения для системы ограничений (2)');

Случайные свободные члены в системе ограничений

Немного усложним задачу — предположим, что свободные члены в системе ограничений являются случайными величинами, имеющими нормальное распределение. При этом их математические ожидания будут равны значениям из предыдущей задачи:

Когда мы оптимизируем целевую функцию, мы можем попасть или не попасть в допустимую область с некоторой вероятностью, поэтому не имеет никакого смысла требовать безусловного попадания в эту область. Единственное правильное действие — задать вероятность попадания в эту область. Пусть эта вероятность будет равна 0.9, тогда система ограничений может быть переписана следующим образом:

По известным законам распределения и заданным вероятностям, можно легко найти нужные квантили:

print(f'a = {norm.ppf(0.1, 1200, 100):.2f}')
print(f'b = {norm.ppf(0.1, 200, 25):.2f}')

a = 1071.84
b = 167.96

Благодаря найденным квантилям, можно заменить (4) на следующий детерминированный эквивалент:

Значит, что по-прежнему можно воспользоваться привычными решателями:

def expr(x):
    return -(27*x[0] + 35*x[1])

def constr_1(x):
    return -1071.84 + 2*x[0] + 5*x[1]

def constr_2(x):
    return -167.96 + 0.5*x[0] + 0.25*x[1]

con_1 = {'type': 'eq', 'fun': constr_1}
con_2 = {'type': 'eq', 'fun': constr_2}

cons = (con_1, con_2)

x_0 = np.ones(2)
result = optimize.minimize(expr, x0=x_0, method='SLSQP', constraints=cons,
                           options={'maxiter':10000})['x']
result

array([285.92, 100.  ])

Кажется, что-то пошло не так - ведь значение второй переменной не изменилось. На самом деле для этого изменения нет никаких причин, так как для каждого из неравенств в (4) используется одно и то же значение вероятности. С учетом симметричности нормального распределения это приводит к тому, что допустимая область просто смещается вверх по оси ординат. Продемонстрируем это с помощью следующего графика:

x2 = np.linspace(0, 300, 300)
X_opt, Y_opt = [], []
for _ in range(1000):
    A = norm.rvs(1200, 100)
    B = norm.rvs(200, 25)
    x11 = 0.5*(A - 5*x2)
    x12 = 2*(B - 0.5*x2)
    opt = (A - 4*B)/3
    plt.plot(x2[x2>opt], x11[x2>opt], color='tab:olive', alpha=0.03, zorder=1)
    plt.plot(x2[x2<opt], x12[x2<opt], color='tab:olive', alpha=0.03, zorder=1)
    X_opt.append(opt)
    Y_opt.append(0.5*(A - 5*opt))

plt.scatter(X_opt, Y_opt, c='tab:olive', s=5, zorder=2)

x11 = 0.5*1071.84-2.5*x2
x12 = 2*167.96 - 0.5*x2
plt.plot(x2[x2>100], x11[x2>100], color='r')
plt.plot(x2[x2<100], x12[x2<100], color='r', label=r'$P_{1} = 0.9, \; P_{2} = 0.9$')
plt.scatter(100, 285.92, zorder=100, c='r', s=70)

x11 = 0.5*1200 - 2.5*x2
x12 = 2*200 - 0.5*x2
plt.plot(x2[x2>100], x11[x2>100], color='tab:green')
plt.plot(x2[x2<100], x12[x2<100], color='tab:green', label=r'$P_{1} = 0.5, \; P_{2} = 0.5$')
plt.scatter(100, 350, zorder=100, c='tab:green', s=70)

x11 = 0.5*1284.16 - 2.5*x2
x12 = 2*241.12 - 0.5*x2
plt.plot(x2[x2>80], x11[x2>80], color='tab:purple')
plt.plot(x2[x2<80], x12[x2<80], color='tab:purple', label=r'$P_{1} = 0.2, \; P_{2} = 0.05$')
plt.scatter(79.92, 442.28, zorder=100, c='tab:purple', s=70)


plt.xlim(0, 300)
plt.ylim(0, 550)

plt.ylabel(r'$x_{1}$', fontsize=15, rotation=0, labelpad=15)
plt.xlabel(r'$x_{2}$', fontsize=15, rotation=0)

plt.title('Графическая интерпретация решения для системы ограничений (4)')

plt.legend();

Данный график хорошо показывает, как в условиях неопределенности мы можем управлять рисками: если риск выхода из допустимой области связан с большими издержками, то красная линия соответствует более сдержанному решению. Данное решение приведет к тому, что мы будем попадать в допустимую область 9 раз из 10, но за это придется заплатить заметным снижением величины целевой функции.

Случайная природа свободных членов привела к "размытию" границы области допустимых значений. В оптимальности найденных значений легко убедиться, если провести множество экспериментов:

n = 100000
p1 = np.sum(np.array([2*result[0] + 5*result[1]]*n) < norm.rvs(1200, 100, n))/n
p2 = np.sum(np.array([0.5*result[0] + 0.25*result[1]]*n) < norm.rvs(200, 25, n))/n
print(f'P1 = {p1:.3f}')
print(f'P2 = {p2:.3f}')

P1 = 0.900
P2 = 0.901

Случайные коэффициенты в системе ограничений

Детерминированные эквиваленты значительно облегчают процесс решения. Фактически, решая задачи стохастического программирования, мы разбиваем процесс решения на два этапа: преобразование задачи к ее детерминированному эквиваленту, а затем решение полученной задачи. А если процесс преобразования к детерминированному виду сам по себе является непростой задачей?

Предположим, что коэффициенты при переменной в системе ограничений стали случайными величинами, имеющими непрерывное равномерное распределение. Как и прежде, математические ожидания этих распределений будут равны значениям из предыдущего примера:

Кажется, что, как и в предыдущем примере, достаточно найти необходимые квантили для в каждом из неравенств. Однако здесь мы как раз и сталкиваемся с арифметическими действиями над случайными величинами, о которых говорилось выше - значит нужно исследовать и учитывать форму результирующего распределения.

Все переменные изменяются линейно, что является преимуществом - значит нам достаточно исследовать результирующее распределение в одной из точек, чтобы определить его форму. Преобразуем первое неравенство из системы ограничений:

Взглянем, как будет распределено значение выражения слева от знака неравенства:

data =  uniform.rvs(1.8, 0.4, 500000)*result[0] + 5*result[1] - norm.rvs(1200, 100, 500000)
sns.histplot(data,stat='density', label='Тest data')
x = np.linspace(-600, 300, 500)
plt.plot(x, norm.pdf(x, *norm.fit(data)), color='r',zorder=100, label='pdf norm. fit. data')
plt.legend();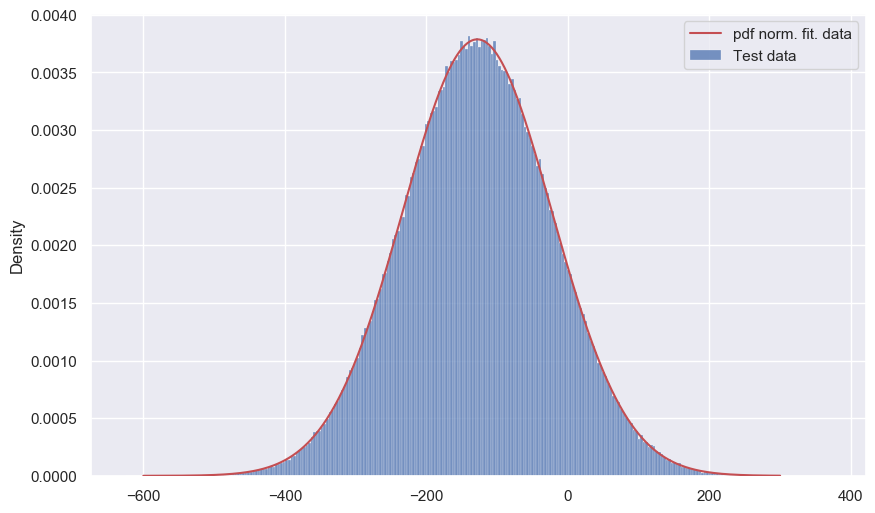

Это результирующее распределение можно было бы принять как нормальное (нет ничего, что указывает на обратное), но это только в данной задаче, ведь при других параметрах мы можем получить гораздо большие отклонения. Например, при и увидим следующее:

data = uniform.rvs(-1, 5, 500000) - norm.rvs(1, 0.75, 500000)
sns.histplot(data,stat='density', label=r'Test data ($N(1, 0.75^{2}) - U(-1, 4)$)')
x = np.linspace(-5, 6, 500)
plt.plot(x, norm.pdf(x, *norm.fit(data)), color='r',zorder=100, label='pdf norm. fit. data')
plt.plot(x, norm.pdf(x, 1, 0.75), label=r'pdf $N(1, 0.75^{2})$')
plt.plot(x, uniform.pdf(x, -1, 5), label=r'pdf $U(-1, 4)$')
plt.legend();

На графике видно, что мы получаем уменьшение эксцесса за счет "поджатия хвостов". Таким образом, лучше перестраховаться и определить форму результирующего распределения.

В случае суммы (разности) двух случайных величин результирующее распределение может быть получено по следующей формуле:

Например, для композиции нормального и равномерного распределения получим следующее выражение:

Которое и является необходимым распределением, в чем легко убедиться:

data = uniform.rvs(-1, 5, 100000) - norm.rvs(1, 0.75, 100000)
sns.histplot(data, stat='density', alpha=0.3, label=r'Test data ($N(1, 0.75^{2}) - U(-1, 4)$)')
x = np.linspace(-5, 10, 500)
plt.plot(x, norm.pdf(x, 1, 0.75), label=r'pdf $N(1, 0.75^{2})$')
plt.plot(x, norm.pdf(x, *norm.fit(data)), color='r',zorder=100, label='pdf norm. fit. data')
plt.plot(x, uniform.pdf(x, -1, 5), label=r'pdf $U(-1, 4)$')
z = (norm.cdf((4 - (x + 1))/0.75) - norm.cdf((-1 - (x + 1))/0.75))/5
plt.plot(x, z, label=r'pdf $N(1, 0.75^{2}) - U(-1, 4)$')
plt.legend();

Вернемся к решению, выполнив еще одно преобразование в выражении (8), а именно представим выражение , в котором , в виде одной случайной величины , зависящей от двух переменных .

В результате получаем следующее неравенство:

Выражение в данном неравенстве можно представить в следующей форме:

Построим график для :

mu = 1200
sigma = 100
a = 1.8*result[0] + 5*result[1]
b = 2.2*result[0] + 5*result[1]
data = uniform.rvs(a, b-a, 500000) - norm.rvs(1200, 100, 500000)
sns.histplot(data,stat='density', label=r'Test data')

x = np.linspace(-600, 400, 500)
plt.plot(x, norm.pdf(x, *norm.fit(data)), color='r', lw=3, alpha=0.7,
         label='pdf norm. fit. data')

z = (norm.cdf((b - (x + mu))/sigma) - norm.cdf((a - (x + mu))/sigma))/(b-a)
plt.plot(x, z, lw=1, c='k', label=r'pdf $g_{1}(z)$')
plt.legend();

Распределение на графике лишь немного отличается от нормального приближения. Выигрыш от такого "подгона" неочевиден, но смысл заключается именно в том, чтобы показать, как благодаря композиции распределений можно заменить стохастическую форму на детерминированную. В нашем случае мы можем заменить:

На:

Если проделать все то же самое для второго неравенства из системы ограничений, то получим следующую картину:

mu = 200
sigma = 25
a = 0.2*result[0] + 0.25*result[1]
b = 0.8*result[0] + 0.25*result[1]
data = uniform.rvs(a, b - a, 500000) - norm.rvs(200, 25, 500000)
sns.histplot(data,stat='density', label=r'Test data')

x = np.linspace(-250, 250, 500)
plt.plot(x, norm.pdf(x, *norm.fit(data)), color='r', lw=3, alpha=0.7,
         label='pdf norm. fit. data')

z = (norm.cdf((b - (x + mu))/sigma) - norm.cdf((a - (x + mu))/sigma))/(b-a)
plt.plot(x, z, lw=1, c='k', label=r'pdf $g_{2}(z)$')
plt.legend();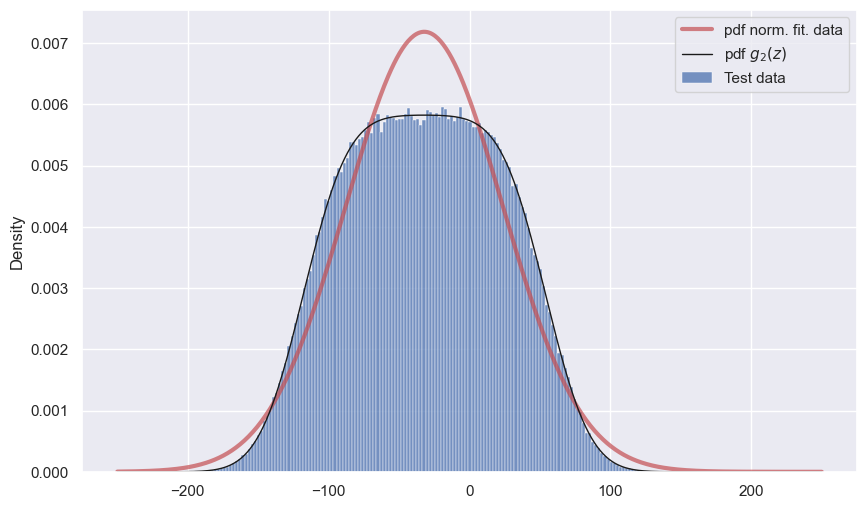

Теперь разница более чем заметная.

Результирующая система ограничений примет следующий вид:

Или, если записать ее в полной форме, то выглядеть она будет так:

Получить ее детерминированный эквивалент оказалось гораздо сложнее - стоило немного усложнить стохастическую модель. Со стороны вычислений все тоже несколько усложнилось, так как теперь на каждом шаге оптимизации придется выполнять численное интегрирование. Тем не менее, для оптимизации можно воспользоваться все тем же привычным решателем:

def expr(x):
    return -(27*x[0] + 35*x[1])

def constr_1(x):
    a = 1.8*x[0] + 5*x[1]
    b = 2.2*x[0] + 5*x[1]
    if (b - a) == 0:
        b = 1e-10
    t = np.linspace(-600, 300, 500)
    z = (norm.cdf((b - (t + 1200))/100) - norm.cdf((a - (t + 1200))/100))/(b-a)
    p = np.trapz(z[t<0], t[t<0])
    return p - 0.9

def constr_2(x):
    a = 0.2*x[0] + 0.25*x[1]
    b = 0.8*x[0] + 0.25*x[1]
    if (b - a) == 0:
        b = 1e-10
    t = np.linspace(-300, 300, 500)
    z = (norm.cdf((b - (t + 200))/25) - norm.cdf((a - (t + 200))/25))/(b-a)
    p = np.trapz(z[t<0], t[t<0])
    return p - 0.9


con_1 = {'type': 'eq', 'fun': constr_1}
con_2 = {'type': 'eq', 'fun': constr_2}

cons = (con_1, con_2)

x_0 = np.array([250, 100])
result = optimize.minimize(expr, x0=x_0, method='SLSQP', constraints=cons,
                           options={'maxiter':5000})['x']
result

array([216.59536991, 126.69359178])

Переменная сильно уменьшилась, а переменная увеличилась. Все дело в случайной природе коэффициента перед , из-за чего одна из границ области допустимых значений размывается еще сильнее:

x2 = np.linspace(0, 300, 300)
X_opt, Y_opt = [], []
for _ in range(1000):
    A = norm.rvs(1200, 100)
    B = norm.rvs(200, 25)
    c11 = uniform.rvs(1.8, 0.4)
    c21 = uniform.rvs(0.2, 0.6)
    x11 = (A - 5*x2)/c11
    x12 = (B - 0.25*x2)/c21
    opt = (A*c21 - B*c11)/(5*c21 - 0.25*c11)
    plt.plot(x2[x2>opt], x11[x2>opt], color='tab:olive', alpha=0.03, zorder=1)
    plt.plot(x2[x2<opt], x12[x2<opt], color='tab:olive', alpha=0.03, zorder=1)
    X_opt.append(opt)
    Y_opt.append((A - 5*opt)/c11)

plt.scatter(X_opt, Y_opt, c='tab:olive', s=5, zorder=2)


X1 = np.linspace(0, 300, 200)
X2 = [150, 200]

mu = 200
sigma = 25
x = np.linspace(-300, 300, 1000)

y = []
res_x = []
for x2 in X2:
    for x1 in X1:
        a = 0.2*x1 + 0.25*x2
        b = 0.8*x1 + 0.25*x2
        if (b - a) != 0:
            z = (norm.cdf((b - (x + mu))/sigma) - norm.cdf((a - (x + mu))/sigma))/(b-a)
            p = np.trapz(z[x<0], x[x<0])
            if p < 0.9:
                y.append(x1)
                res_x.append(x2)
                break

mu = 1200
sigma = 100
x = np.linspace(-600, 300, 1000)

y_1 = []
res_x_1 = []
for x2 in X2:
    for x1 in X1:
        a = 1.8*x1 + 5*x2
        b = 2.2*x1 + 5*x2
        if (b - a) != 0:
            z = (norm.cdf((b - (x + mu))/sigma) - norm.cdf((a - (x + mu))/sigma))/(b-a)
            p = np.trapz(z[x<0], x[x<0])
            if p < 0.9:
                y_1.append(x1)
                res_x_1.append(x2)
                break

res_x, y
a1 = -(y[0] - y[1])/(res_x[1] - res_x[0])
b1 = -(res_x[0]*y[1] - res_x[1]*y[0])/(res_x[1] - res_x[0])
a2 = -(y_1[0] - y_1[1])/(res_x_1[1] - res_x_1[0])
b2 = -(res_x_1[0]*y_1[1] - res_x_1[1]*y_1[0])/(res_x_1[1] - res_x_1[0])

x2 = np.linspace(0, 300, 300)
x12 = a1*x2 + b1
x11 = a2*x2 + b2
plt.plot(x2[x2>result[1]], x11[x2>result[1]], color='r')
plt.plot(x2[x2<result[1]], x12[x2<result[1]], color='r', label=r'$P_{1} = 0.9, \; P_{2} = 0.9$')
plt.scatter(result[1], result[0], zorder=100, c='r', s=70)

plt.xlim(0, 300)
plt.ylim(0, 650)

plt.ylabel(r'$x_{1}$', fontsize=15, rotation=0, labelpad=15)
plt.xlabel(r'$x_{2}$', fontsize=15, rotation=0)

plt.title('Графическая интерпретация решения для системы ограничений (14)')

plt.legend();

Глядя на этот график, кажется, что красная линия должна быть выше. Однако, если провести множество экспериментов, то мы лишь подтверждаем, что она расположена там, где и должна быть:

n = 100000
p1 = np.sum(uniform.rvs(1.8, 0.4, n)*result[0] + 5*result[1] < norm.rvs(1200, 100, n))/n
p2 = np.sum(uniform.rvs(0.2, 0.6, n)*result[0] + .25*result[1] < norm.rvs(200, 25, n))/n
print(f'P1 = {p1:.3f}')
print(f'P2 = {p2:.3f}')

P1 = 0.902
P2 = 0.903

Предположим, что сами переменные являются нормально-распределенными величинами: допустим, и . Может показаться, что из-за этого придется выбрать еще более умеренные значения для и , но это не так:

x2 = np.linspace(0, 200, 300)
X_opt, Y_opt = [], []
for _ in range(1000):
    A = norm.rvs(1200, 100)
    B = norm.rvs(200, 25)
    c11 = uniform.rvs(1.8, 0.4)
    c21 = uniform.rvs(0.2, 0.6)
    x11 = (A - 5*x2)/c11
    x12 = (B - 0.25*x2)/c21
    opt = (A*c21 - B*c11)/(5*c21 - 0.25*c11)
    plt.plot(x2[x2>opt], x11[x2>opt], color='tab:olive', alpha=0.03, zorder=1)
    plt.plot(x2[x2<opt], x12[x2<opt], color='tab:olive', alpha=0.03, zorder=1)
    X_opt.append(opt)
    Y_opt.append((A - 5*opt)/c11)

x = [219.5, 123]
n = 1000
X1 = norm.rvs(x[1], 10, n)
X2 = norm.rvs(x[0], 10, n)

plt.scatter(X1, X2, c='r', s=1, alpha=0.5, zorder=2)
plt.axvline(x[1], c='r', lw=1, ls='--')
plt.axhline(x[0], c='r', lw=1, ls='--')

plt.ylabel(r'$x_{1}$', fontsize=15, rotation=0, labelpad=15)
plt.xlabel(r'$x_{2}$', fontsize=15, rotation=0)

plt.title('Графическая интерпретация решения для системы ограничений (14)\n\
с переменными, испытывающими случайные отклонения')

plt.xlim(0, 200)
plt.ylim(0, 600);

Полученный результат снова соответствует нашим требованиям, хоть и выглядит нелогичным:

n = 1000000
x = [219.5, 123]
p1 = np.sum(uniform.rvs(1.8, 0.4, n)*norm.rvs(x[0], 10, n) + 5*norm.rvs(x[1], 10, n) < norm.rvs(1200, 100, n))/n
p2 = np.sum(uniform.rvs(0.2, 0.6, n)*norm.rvs(x[0], 10, n) + .25*norm.rvs(x[1], 10, n) < norm.rvs(200, 25, n))/n
print(f'P1 = {p1:.3f}')
print(f'P2 = {p2:.3f}')

P1 = 0.895
P2 = 0.895

Несмотря на то, что сами переменные могут испытывать случайные отклонения, нет необходимости уменьшать их значение, а значит и значение целевой функции также будет максимальным. Небольшая оговорка: теперь максимальным будет среднее значение целевой функции. Действительно, если раньше значением целевой функции:

Было детерминированным, то после того как переменные стали случайными:

Ее значение также стало случайным, причем распределенным как:

В чем также достаточно легко убедиться:

v = np.linspace(8500, 12000, 300)
y = norm.pdf(v, 27*x[0] + 35*x[1], ((27*10)**2 + (35*10)**2)**0.5)
plt.plot(v, y, c='r', label=r'pdf($z(X_{1}, X_{2})$)')
plt.xlabel(r'$z(X_{1}, X_{2})$')
data = 27*norm.rvs(x[0], 10, 100000) + 35*norm.rvs(x[1], 10, 100000)
sns.histplot(data, stat='density')
plt.legend();

Если заранее известно, что значение целевой функции является случайным, то как убедиться, что значения переменных и действительно оптимальны? Единственный способ выяснить это - разобраться в том, как были получены представленные решения или попытаться найти их самостоятельно. Допустим, указанное выше решение нам предоставлено неким лицом, которое хочет, чтобы мы верили ему на слово, а мы этого не хотим. Тогда, проделав все математические выкладки, мы придем к следующему коду:

def expr(x):
    #print(x)
    return -(27*x[0] + 35*x[1])

def constr_1(x):
    # параметры U(1.8; 2.2)-dist
    a, b = 1.8, 2.2
    # ограничения для pdf(N(x_1, 10))
    l_1, r_1 = norm.ppf(0.001, x[0], 10), norm.ppf(0.999, x[0], 10)
    # Значения mu и sigma для 5*N(x_2; 10^2) - N(1200; 100^2)
    mu, sigma = 5*x[1] - 1200, ((5*10)**2 + 100**2)**0.5
    # ограничения для pdf(5*N(x_2; 10^2) - N(1200; 100^2))
    l_2, r_2 = norm.ppf(0.001, mu, sigma), norm.ppf(0.999, mu, sigma)
    n = 1000
    X = np.linspace(l_1, r_1, n)
    Z_1 = np.linspace(a*l_1, b*r_1, n)
    F_1 = np.trapz(norm.pdf(X, x[0], 10)*uniform.pdf(np.c_[Z_1] / X, a, b - a) / np.abs(X), x=X, axis=1)

    Z_2 = np.linspace(Z_1[0] + l_2, Z_1[-1] + r_2, n)
    F_2 = np.trapz(F_1 * norm.pdf(np.c_[Z_2] - Z_1, mu, sigma), x=Z_1, axis=1)
    p = np.trapz(F_2[Z_2 < 0], Z_2[Z_2 < 0])
    return p - 0.9

def constr_2(x):
    # параметры U(0.2; 0.8)-dist
    a, b = 0.2, 0.8
    # ограничения для pdf(N(x_1, 10))
    l_1, r_1 = norm.ppf(0.001, x[0], 10), norm.ppf(0.999, x[0], 10)
    # Значения mu и sigma для 0.25*N(x_2; 10^2) - N(200; 25^2)
    mu, sigma = 0.25*x[1] - 200, ((0.25*10)**2 + 25**2)**0.5
    # ограничения для pdf(0.25*N(x_2; 10^2) - N(200; 25^2))
    l_2, r_2 = norm.ppf(0.001, mu, sigma), norm.ppf(0.999, mu, sigma)
    n = 1000
    X = np.linspace(l_1, r_1, n)
    Z_1 = np.linspace(a*l_1, b*r_1, n)
    F_1 = np.trapz(norm.pdf(X, x[0], 10)*uniform.pdf(np.c_[Z_1] / X, a, b - a) / np.abs(X), x=X, axis=1)

    Z_2 = np.linspace(Z_1[0] + l_2, Z_1[-1] + r_2, n)
    F_2 = np.trapz(F_1 * norm.pdf(np.c_[Z_2] - Z_1, mu, sigma), x=Z_1, axis=1)
    p = np.trapz(F_2[Z_2 < 0], Z_2[Z_2 < 0])
    return p - 0.9


con_1 = {'type': 'ineq', 'fun': constr_1}
con_2 = {'type': 'ineq', 'fun': constr_2}

cons = (con_1, con_2)

x_0 = np.array([200, 100])
result = optimize.minimize(expr, x0=x_0, method='COBYLA', constraints=cons, 
                           options={'maxiter':1000})
result['x']

array([216.9568369 , 123.05691693])

В результате мы получаем, что теперь равно 217, а не 219.5, а значение практически не изменилось. Выполнив проверку:

n = 1000000
x = [217, 123]
p1 = np.sum(uniform.rvs(1.8, 0.4, n)*norm.rvs(x[0], 10, n) + 5*norm.rvs(x[1], 10, n) < norm.rvs(1200, 100, n))/n
p2 = np.sum(uniform.rvs(0.2, 0.6, n)*norm.rvs(x[0], 10, n) + .25*norm.rvs(x[1], 10, n) < norm.rvs(200, 25, n))/n
print(f'P1 = {p1:.3f}')
print(f'P2 = {p2:.3f}')

P1 = 0.903
P2 = 0.903

Убеждаемся в том, что найденное решение гарантированно удовлетворяет условию о вероятности попадания в допустимую область, но значение целевой функции становится несколько меньше:

print('27*219.5 + 35*123 =', 27*219.5 + 35*123)
print('27*217 + 35*123 =', 27*217 + 35*123)

27*219.5 + 35*123 = 10231.5
27*217 + 35*123 = 10164

Причина отличия в представленных ответах заключается в реализации численных методов. В стохастических задачах мы имеем дело с выполнением арифметических операций над случайными величинами. Если известны распределения плотности случайных величин, то результат выполнения арифметических операций (например, сложения и умножения) может быть получен с помощью следующих правил:

одного интеграла. Хорошо, если распределения являются простыми и их немного, но зачастую распределений много, и задаются они специальными функциями. Именно поэтому получение детерминированного эквивалента стохастической задачи в аналитической форме не всегда возможно. В свою очередь это означает, что возникает проблема выбора между скоростью вычислений и их точностью.

Следует обратить внимание на два важных следствия применения стохастического программирования:

1. Значение целевой функции может быть случайным - это означает лишь то, что у данной случайности существует математическое описание. Только это описание может служить оправданием в случае отклонения реализованных значений от ожидаемых. Впрочем, сам пример показывает, что ожидать какого-то конкретного значения не имеет смысла.

2. Возникает дилемма между улучшением результата целевой функции и ухудшением гарантий о доле попаданий в допустимую область - это означает, что выбор подходящего квантиля также является задачей оптимизации. Например, в нашем примере квантиль равен 0.9, но это значение является абсолютно произвольным. Если бы речь шла о человеческих жизнях, то он мог бы быть равен 1.0 или 0.0, а если бы речь шла о шариках для пинг-понга, то он запросто мог бы быть равен 0.3 или 0.5. Все зависит от убытков, которые связаны с выходом за границы допустимой области или слишком большим погружением в нее.

Любые дальнейшие примеры по вводу в модель новых случайных компонент все равно приводили бы нас к процессу преобразования из стохастической формы в детерминированную. П о мере усложнения модели в аналитической форме все это привело бы к крайне громоздким формулам, но эта проблема решается благодаря численному интегрированию и простым правилам композиции распределений.

Главный вывод, который сейчас можно сделать, заключается в том, что интуитивные решения здесь не работают от слова совсем. Конечно, интуиция - понятие субъективное, но, как правило, мы стремимся избавиться от неопределенности ввиду психологического дискомфорта, который неизбежно с ней связан.

Реалистичный пример

Представим, что у нас есть логистическая компания, выполняющая междугородние перевозки грузов. Нам предстоит заключить контракт с неким клиентом на месяц, которому нужно перевезти груз по двум направлениям. Клиенту необходимо в течение месяца перевезти тонн груза по первому направлению и тонн по второму. При этом клиент сообщает, что указанные величины случайны и распределены как: и . Транспортировка выполняется на грузовиках, которых в нашем парке очень много: первого типа и второго типа. Необходимо найти такой оптимальный набор назначений грузовиков по направлениям, который минимизирует наши расходы.

Предположим, что мы пропустили информацию о некоторых распределениях мимо ушей и решили оптимизировать по старинке. Если это так, то у нас имеется какая-никакая бухгалтерия. Однако мы привыкли всегда ориентироваться на средние значения:

• расходы на каждый тип грузовиков по каждому направлению (тыс. рублей): ;

• грузооборот каждого типа грузовиков по каждому направлению (тонн): .

Получаем простенькую задачу дискретного программирования, которая может быть решена простым перебором:

res = np.inf
for x1 in range(70):
    for x2 in range(30):
        if 78*x1+82*x2 >= 2800:
            for x3 in range(70-x1):
                for x4 in range(30-x2):
                    if 89*x3+96*x4 >= 3600:
                        tmp = 648*x1 + 661*x2 + 683*x3 + 706*x4
                        if tmp < res:
                            res = tmp
                            X = [x1, x2, x3, x4]
print('X =', X)
print('cost =', res)
print('cargo_1 =', 78*X[0] + 82*X[1])
print('cargo_1 =', 89*X[2] + 96*X[3])

X = [17, 18, 34, 6]
cost = 50372
cargo_1 = 2802
cargo_1 = 3602

Получаем, что при достигается необходимый минимум в 50.372.000 рублей, при этом мы укладываемся в среднее значение массы перевозимого груза. Эти объемы являются случайными, скажете вы, но так это оно всегда так было: будет меньше  — погоним грузовики в другое место, будет больше — пригоним с другого места и довезем. Делов-то!

А если быть повнимательнее?

Разумный вопрос: а вдруг клиент все-таки неспроста указал на то, что и ? При этом клиент говорил о том, что груз не является однородным, а значит и грузооборот также может быть разным. И еще грузовики иногда ломаются, а водители могут заболеть. Все это поправимо, но так или иначе влияет на грузооборот и затраты, которые тоже следует воспринимать как случайные величины. Если "поднять" бухгалтерию, то окажется, что так и есть. Может быть, стоит принять все это во внимание и пересчитать?

Допустим, что после обработки данных из бухгалтерии выяснилось следующее:

• расходы: , , , ;

• грузооборот: , , , .

Тогда цель задачи немного меняется - нужно минимизировать математическое ожидание расходов:

Как быть с условиями? Контракт заключается на месяц, соответственно, и весь груз, несмотря на его случайный тоннаж, также должен быть перевезен за это время. Чтобы гарантировать это, нужно принять массу груза по каждому направлению как и (то есть увеличенные на ), а грузооборот разных типов грузовиков по каждому направлению должен быть взят по нижним границам их равномерных распределений (). Только в этом случае мы можем гарантировать, что груз будет доставлен в полном объеме точно в срок. Ограничения будут выглядеть следующим образом:

res = np.inf
for x1 in range(70):
    for x2 in range(30):
        if 74*x1+76*x2 >= 3400:
            for x3 in range(70-x1):
                for x4 in range(30-x2):
                    if 85*x3+90*x4 >= 4500:
                        tmp = 0.5*((630+670)*x1 + (640+680)*x2 + (660+700)*x3 + (680+720)*x4)
                        if tmp < res:
                            res = tmp
                            X = [x1, x2, x3, x4]
print('X =', X)
print('cost =', res)
print('cargo_1 =', 74*X[0] + 76*X[1])
print('cargo_1 =', 85*X[2] + 90*X[3])

X = [33, 13, 36, 16]
cost = 65710.0
cargo_1 = 3430
cargo_1 = 4500

Для обеспечения таких гарантий уже потребуется задействовать практически все имеющиеся грузовики, а именно: . При этом средние минимальные затраты возрастут до 65.710.000 рублей.

Возможно, клиент все понимает и, чтобы не платить огромные деньги за такие гарантии, он готов немного увеличить время транспортировки? Что произойдет, если мы будем гарантировать безусловную перевозку всего объема груза только в 90% случаев? Можем предложить решение для оставшихся 10% случаев: если что-то и останется, то мы перевезем остатки в течение недели по отдельному договору. В таком случае задача по поиску , гарантирующего перевозку всего объема груза в 9 случаях из 10, приобретет вид:

def p_constr(x1, x2, a1, b1, a2, b2, mu, sigma):
    A1, B1 = a1*x1, b1*x1
    A2, B2 = a2*x2, b2*x2
    n = 50
    Z_1 = np.linspace(A1, B1, n)
    Z_2 = np.linspace(A1 + A2, B1 + B2, n)
    f_1 = uniform.pdf(Z_1, A1, B1 - A1)
    f_2 = uniform.pdf(np.c_[Z_2] - Z_1, A2, B2 - A2)
    F_1 = np.trapz(f_1 * f_2, x=Z_1, axis=1)
    l =  norm.ppf(0.999, mu, sigma) - A1 - A2
    r =  norm.ppf(0.001, mu, sigma) - B1 - B2
    Z_3 = np.linspace(l, r, n)
    f_3 = norm.pdf(np.c_[Z_3] + Z_2, mu, sigma)
    F_2 = np.trapz(F_1 * f_3, x=Z_2, axis=1)
    Z_3 = -Z_3
    return np.trapz(F_2[Z_3 > 0], Z_3[Z_3 > 0])

res = np.inf
for x1 in range(1, 70):
    for x2 in range(1, 30):
        p1 = p_constr(x1, x2, 74, 82, 76, 88, 2800, 200)
        if 0.9 < p1 < 0.93:
            for x3 in range(1, 70-x1):
                for x4 in range(1, 30-x2):
                    p2 = p_constr(x3, x4, 85, 93, 90, 102, 3600, 300)
                    if 0.9 < p2 < 0.93:
                        tmp = 0.5*((630+670)*x1 + (640+680)*x2 + (660+700)*x3 + (680+720)*x4)
                        if tmp < res:
                            res = tmp
                            X = [x1, x2, x3, x4]
print('X =', X)
print('cost =', res)
print('mean_cargo_1 =', 78*X[0] + 82*X[1])
print('mean_cargo_2 =', 89*X[2] + 96*X[3])

X = [30, 9, 33, 11]
cost = 55580.0
mean_cargo_1 = 3078
mean_cargo_2 = 3993

Такие гарантии в среднем обойдутся значительно дешевле и составят 55.580.000 рублей, что на 10 миллионов меньше предыдущего результата. Тем не менее, такое сравнение не совсем корректно, ведь в 10% случаев мы не сможем перевезти весь груз в течение месяца, а значит за транспортировку остатков тоже придется заплатить.

Двухэтапное стохастическое программирование

Гораздо выгоднее отказаться от попыток перевезти груз полностью в течение месяца и разбить решение на два этапа. На первом этапе мы находим решение, подразумевающее наличие остатка груза, а на втором - находим решение, компенсирующее эту невязку.

Чаще всего невязка считается детерминированной (принимается), и на момент завершения первого этапа и реализуются. Это значительно облегчает решение второго этапа, но мы поступим несколько иначе: в приведенном выше решении мы уже строим распределения плотности вероятности для результирующего значения каждого из ограничений. Например, для найденного выше решения распределение по первому ограничению будет иметь следующий вид:

x_11, x_12 = 30, 9
a_11, b_11 = 74*x_11, 82*x_11
a_12, b_12 = 76*x_12, 88*x_12

n = 100

Z_1 = np.linspace(a_11, b_11, n)
Z_2 = np.linspace(a_11 + a_12, b_11 + b_12, n)
f_1 = uniform.pdf(Z_1, a_11, b_11 - a_11)
f_2 = uniform.pdf(np.c_[Z_2] - Z_1, a_12, b_12 - a_12)
F_1 = np.trapz(f_1 * f_2, x=Z_1, axis=1)

mu, sigma = 2800, 200
l =  norm.ppf(0.999, mu, sigma) - a_11 - a_12
r =  norm.ppf(0.001, mu, sigma) - b_11 - b_12
Z_3 = np.linspace(l, r, n)
f_3 = norm.pdf(np.c_[Z_3] + Z_2, mu, sigma)
F_2 = np.trapz(F_1 * f_3, x=Z_2, axis=1)
Z_3 = -Z_3


plt.plot(Z_3, F_2, c='b')
plt.axvline(0, c='r')
plt.axhline(0, c='k', lw=1)
plt.fill_betweenx(F_2[Z_3 < 0], Z_3[Z_3 < 0], alpha=0.5);

Данный график показывает, что 90% площади под результирующей кривой соответствует гарантированной доставке всего объема груза по первому направлению, а закрашенная область показывает, как будут распределены остатки в оставшихся 10% случаев. По новому условию мы должны гарантированно перевезти именно остаток груза.

Понимая вероятность наличия невязки, необходимо определить следующие параметры:

• недельный грузооборот каждого типа грузовика по каждому направлению: , , , ;

• недельные расходы на каждый тип грузовика по каждому направлению: , , , ;

Теперь мы можем записать двухэтапную задачу в следующей форме:

где - это расстановка грузовиков, гарантирующая перевозку максимально возможного остатка при заданном . Найти решение нужно при соблюдении следующих условий:

где, и - реализации случайных параметров и .

def second_phase(rem_1, rem_2):
    res = np.inf
    for y1 in range(70):
        for y2 in range(30):
            if 18*y1+19*y2 >= rem_1:
                for y3 in range(70-y1):
                    for y4 in range(30-y2):
                        if 21*y3+22*y4 >= rem_2:
                            tmp = 0.5*((158+168)*y1 + (160+170)*y2 + (165+175)*y3 + (170+180)*y4)
                            if tmp < res:
                                res = tmp
                                Y = [y1, y2, y3, y4]
    return Y
    
def rem(x1, x2, a1, b1, a2, b2, mu, sigma):
    A1, B1 = a1*x1, b1*x1
    A2, B2 = a2*x2, b2*x2
    return norm.ppf(0.999, mu, sigma) - A1 - A2

def p_constr(x1, x2, a1, b1, a2, b2, mu, sigma):
    A1, B1 = a1*x1, b1*x1
    A2, B2 = a2*x2, b2*x2
    n = 100
    Z_1 = np.linspace(A1, B1, n)
    Z_2 = np.linspace(A1 + A2, B1 + B2, n)
    f_1 = uniform.pdf(Z_1, A1, B1 - A1)
    f_2 = uniform.pdf(np.c_[Z_2] - Z_1, A2, B2 - A2)
    F_1 = np.trapz(f_1 * f_2, x=Z_1, axis=1)
    l =  norm.ppf(0.999, mu, sigma) - A1 - A2
    r =  norm.ppf(0.001, mu, sigma) - B1 - B2
    Z_3 = np.linspace(l, r, n)
    f_3 = norm.pdf(np.c_[Z_3] + Z_2, mu, sigma)
    F_2 = np.trapz(F_1 * f_3, x=Z_2, axis=1)
    Z_3 = -Z_3
    p_rem = np.trapz(F_2[Z_3 < 0], Z_3[Z_3 < 0])
    p_entire = np.trapz(F_2[Z_3 > 0], Z_3[Z_3 > 0])
    return l, p_rem, p_entire
'''
res = np.inf
for x1 in range(1, 70):
    for x2 in range(1, 30):
        rem1 = rem(x1, x2, 74, 82, 76, 88, 2800, 200)
        if 0 < rem1 < 700:
            for x3 in range(1, 70-x1):
                for x4 in range(1, 30-x2):
                    rem2 = rem(x3, x4, 85, 93, 90, 102, 3600, 300)
                    if 0 < rem2 < 700:
                        print(x1, x2)
                        param_1 = p_constr(x1, x2, 74, 82, 76, 88, 2800, 200)
                        param_2 = p_constr(x3, x4, 85, 93, 90, 102, 3600, 300)
                        Y = second_phase(rem1, rem2)
                        f1_c1 = 0.5*((630+670)*x1 + (640+680)*x2)*param_1[2]
                        f1_c2 = 0.5*((660+700)*x3 + (680+720)*x4)*param_2[2]
                        f2_c1 = 0.5*((158+168)*Y[0] + (160+170)*Y[1])*param_1[1]
                        f2_c2 = 0.5*((165+175)*Y[2] + (170+180)*Y[3])*param_2[1]
                        tmp = f1_c1 + f1_c2 + f2_c1 + f2_c2
                        if tmp < res:
                            res = tmp
                            X = [x1, x2, x3, x4]
                            S = [X, Y]
'''
# Решение получено в облаке
S = [[28, 9, 23, 18], [21, 15, 37, 8]]
print('Stage_1: X =', S[0])
print('Stage_2: Y =', S[1])

Stage_1: X = [28, 9, 23, 18]
Stage_2: Y = [21, 15, 37, 8]

Теперь мы можем гарантировать, что абсолютно весь груз будет доставлен в оговоренные сроки, а именно за пять недель. Во сколько нам обойдутся такие гарантии? Чтобы узнать это, проведем множество экспериментов:

X = [28, 9, 23, 18]
Y = [21, 15, 37, 8]
COST = []

for _ in range(100000):
    C = uniform.rvs((630, 640, 660, 680), (40, 40, 40, 40))
    A = uniform.rvs((74, 76, 85, 90), (8, 8, 8, 12))
    B = norm.rvs((2800, 3600), (200, 300))
    Q = uniform.rvs((158, 160, 165, 170), (10, 10, 10, 10))

    rem_1 = B[0] - A[0]*X[0] - A[1]*X[1]
    rem_2 = B[1] - A[2]*X[2] - A[3]*X[3]

    cost_i = C[0]*X[0] + C[1]*X[1] + C[2]*X[2] + C[3]*X[3]

    if rem_1 > 0:
        cost_i += Q[0]*Y[0] + Q[1]*Y[1]
    if rem_2 > 0:
        cost_i += Q[2]*Y[2] + Q[3]*Y[3]

    COST.append(cost_i)
    
COST = np.array(COST)

costs_p1 = COST[(COST > 50000) & (COST < 55000)]
plt.axvspan(costs_p1.min(), costs_p1.max(), alpha=0.3, color='b')

costs_p2 = COST[(COST > 55000) & (COST < 62500)]
plt.axvspan(costs_p2.min(), costs_p2.max(), alpha=0.3, color='b')

costs_p3 = COST[(COST > 63000) & (COST < 67500)]
plt.axvspan(costs_p3.min(), costs_p3.max(), alpha=0.3, color='b')

sns.histplot(COST, zorder=10, stat='density')

param_1 = p_constr(28, 9, 74, 82, 76, 88, 2800, 200)
param_2 = p_constr(23, 18, 85, 93, 90, 102, 3600, 300)

p_1 = param_1[2] * param_2[2]
p_2 = param_1[2] * param_2[1] + param_1[1] * param_2[2]
p_3 = param_1[1] * param_2[1]

plt.text(costs_p1.min() + 300, 4e-4, rf'$p_{1} = {p_1:.3f}$', fontsize=13)
plt.text(costs_p2.min() + 300, 2e-4, rf'$p_{2} = {p_2:.3f}$', fontsize=13)
plt.text(costs_p3.min() + 300, 1e-4, rf'$p_{3} = {p_3:.3f}$', fontsize=13)


mean_costs = np.mean(COST)
plt.axvline(mean_costs, color='r', label=f'Средние затраты ({mean_costs: .0f})')

plt.ylim(0, 45e-5)
plt.xlabel('Минимальные затраты (тыс. руб.)')
plt.legend()
plt.title('Распределение минимальных затрат', fontsize=15);

График показывает различные варианты развития событий: остатки груза могут не появиться вовсе, появиться только по одному направлению или появиться сразу на двух направлениях с разной вероятностью. До этого момента эти вероятности не учитывались, хотя именно они придают распределению минимальных затрат такой необычный вид.

Единственный минус данного примера заключается в том, что он решается методом полного перебора, что очень медленно. В следующей статье будет показано, как решать такие задачи гораздо быстрее с помощью метода кросс-энтропии. Также есть языки алгебраического моделирования и солверы, которые позволяют решать определенный круг подобных задач, но, к сожалению, им подвласны далеко не все оптимизационные модели.

Заключение

Цель данной статьи - показать, что стохастическое программирование особенно актуально в наш век больших данных, оно незаурядно и зачастую контринтуитивно.

Математическая статистика нужна нам, чтобы заставить данные говорить, а но стохастическое программирование нужно, чтобы заставить данные работать. Трудно сказать, когда именно стохастическое программирование дает значительное преимущество над детерминированными методами оптимизации: в одном случае положительный эффект может составлять всего сотые доли процентов, а в другом речь будет идти о единицах и даже десятках процентов.

Вопрос целесообразности применения стохастического программирования в системе, где накапливаются данные и выполняется поиск оптимальных решений, должен быть обязательно и тщательно исследован, так как этот подход может привести к крайне положительным результатам по оптимизации ресурсов и средств.