Введение

AMX (Advanced Matrix Extension) - это модуль аппаратного ускорения умножения матриц, который появился в серверных процессорах Intel Xeon Scalable, начиная с 4 поколения (архитектура Sapphire Rapids). 

В начале этого года ко мне в руки наконец попал сервер, с данным типом процессора.

Конкретно модель Xeon(R) Gold 5412U - это 24 ядерный процессор с тактовой частотой в 2.1 GHz. При этом 8 приоритетных ядер могут разгонятся до 2.3 GHz, а 1 ядро до 3.9 GHz в Turbo Boost). Кроме того данный процессор поддерживает 8 канальную DDR-5 4400 MT/s. 

Мне как человеку, достаточно долгое время посвятившему оптимизации алгоритмов компьютерного зрения и запуска нейронный сетей на CPU (библиотеки Simd и Synet), было интересно: на сколько AMX позволяет реально ускорить вычисления и как извлечь из него максимальную производительность.

Далее я постараюсь максимально подробно ответить на данные вопросы. Прежде всего я буду касаться вопросов однопоточной производительности (многопоточную рассмотрю позже). 

Описание AMX

Для начала опишем, что из себя представляет AMX. Он представляет из себя модуль управления (Tile Config), кроме того набор матричных регистров и матричный ускоритель, который производит операции матричного умножения для чисел в формате bfloat16 и int8 (в следующем году ожидается выход процессоров с поддержкой в AMX  умножения чисел в формате float16, в том числе комплексных). 

В текущей реализации присутствуют 8 регистров размером по 1024 байта, которому соответствует максимальный размер матрицы 32x16 (для bfloat16) или 64x16 (для int8).

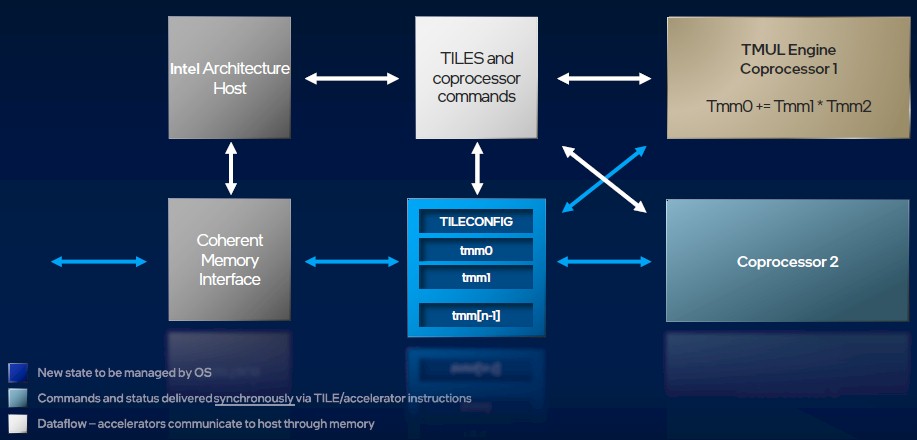
Упомянутый выше управляющий модуль регулируется при помощи 64-х байтного конфигурационного регистра, в котором можно задавать фактический размер каждой матрицы. Операции умножения доступны только между данными, которые находятся в матричных регистрах, кроме того есть специальные операции по загрузке и выгрузке данных.

Формат bfloat16 и умножение матриц

Скажем пару слов о формате bfloat16  - в отличие от формата float16 он имеет мантиссу в 7 бит, но зато с гораздо более широким динамическим диапазоном. По сути это половинка bfloat32 с обрезанной точностью мантиссы.

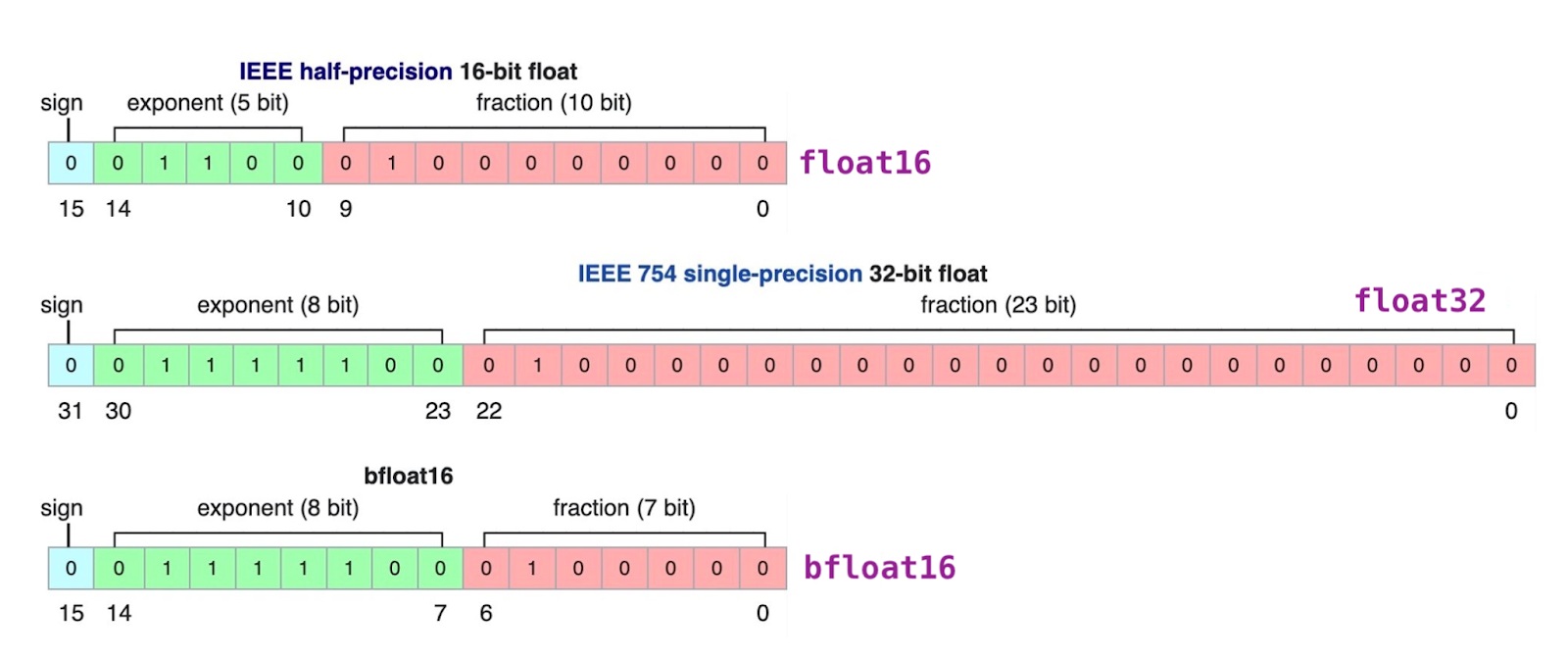
Использование формата bfloat16 приводит к итоговой погрешности порядка 0.2-0.3%, чего впрочем вполне достаточно для целей машинного обучения.

Операция умножения двух матриц можно пояснить следующим псевдокодом:

FOR m = 0 TO dst.rows - 1
    FOR k = 0 TO (a.colsb / 4) - 1
        FOR n = 0 TO (dst.colsb / 4) - 1
            dst[m][n] += FP32(a[m][2 * k + 0]) * FP32(b[k][2 * n + 0])
            dst[m][n] += FP32(a[m][2 * k + 1]) * FP32(b[k][2 * n + 1])

По сути в float32 аккумулятор попарно суммируются произведения входных bfloat16 матриц. Т.е. если мы хотим перемножить две матрицы в формате float32, то первую мы просто конвертируем в bfloat16, а для второй матрицы кроме непосредственно самой конвертации необходимо будет перемешать элементы в четных и нечетных строках.

Простейший пример использования AMX

Ниже приведен простейший пример использования AMX:

#include <immintrin.h>
#include <stdint.h>
#include <iostream>
#include <unistd.h>
#include <sys/syscall.h>

const int ARCH_REQ_XCOMP_PERM = 0x1023;
const int XFEATURE_XTILEDATA = 18;

void ConvertA(const float* src, uint16_t* dst)
{
    __m512 s0 = _mm512_loadu_ps(src + 0 * 16);
    __m512 s1 = _mm512_loadu_ps(src + 1 * 16);
    _mm512_storeu_si512(dst, (__m512i)_mm512_cvtne2ps_pbh(s1, s0));
}

void ConvertB(const float* src, int stride, uint16_t* dst)
{
    static const __m512i PERM_IDX = _mm512_set_epi16(
        0x1f, 0x0f, 0x1e, 0x0e, 0x1d, 0x0d, 0x1c, 0x0c, 
        0x1b, 0x0b, 0x1a, 0x0a, 0x19, 0x09, 0x18, 0x08,
        0x17, 0x07, 0x16, 0x06, 0x15, 0x05, 0x14, 0x04, 
        0x13, 0x03, 0x12, 0x02, 0x11, 0x01, 0x10, 0x00);
    __m512 s0 = _mm512_loadu_ps(src + 0 * stride);
    __m512 s1 = _mm512_loadu_ps(src + 1 * stride);
    __m512i d = (__m512i)_mm512_cvtne2ps_pbh(s1, s0);
    _mm512_storeu_si512(dst, _mm512_permutexvar_epi16(PERM_IDX, d));
} // Конвертация в BF16 с переупорядочиванием четных и нечетных строк.

struct TileConfig
{
    uint8_t paletteId; // должен быть установлен в 1
    uint8_t startRow; // должен быть установлен в 0
    uint8_t reserved[14];
    uint16_t colsb[16]; // актуальная длина строк матриц в байтах
    uint8_t rows[16]; // актуальное число строк в матрицах
};

int main()
{
    // Инициализация AMX в Linux:
    if (syscall(SYS_arch_prctl, 
        ARCH_REQ_XCOMP_PERM, XFEATURE_XTILEDATA) != 0)
    {
        std::cout << "Can't initialize AMX!" << std::endl;
        return 1;
    }

    float A[16][32], B[32][16], C[16][16];

    uint16_t a[16][32];
    for (int i = 0; i < 16; ++i)
        ConvertA(A[i], a[i]);

    uint16_t b[16][32];
    for (int i = 0; i < 16; ++i)
        ConvertB(B[i * 2], 16, b[i]);

    TileConfig conf = {};
    conf.paletteId = 1; 
    conf.rows[0] = 16; 
    conf.colsb[0] = 16 * 4; 
    conf.rows[1] = 16; 
    conf.colsb[1] = 16 * 4;
    conf.rows[2] = 16;
    conf.colsb[2] = 16 * 4;
    _tile_loadconfig(&conf);// Загрузка конфигурации AMX

    _tile_zero(0); // обнуление 0-го рестра

    _tile_loadd(1, a, 64); // загрузка матрицы A в 1-й регистр

    _tile_loadd(2, b, 64); // загрузка матрицы B в 2-й регистр

    _tile_dpbf16ps(0, 1, 2);// непосредственно умножение С += A * B

    _tile_stored(0, C, 64); // сохранение рузультата в матрицу С

    _tile_release(); // очистка AMX конфигурации

    return 0;
}

Давайте его рассмотрим несколько подробнее: 

• Прежде всего нужно включить в операционной системе использование AMX регистров. 

• Далее необходимо преобразовать входные значения матриц A и B из формата float32 в формат bfloat16, для чего есть соответствующие инструкции в наборе AVX-512BF16. Не забываем, что значения четных и нечетных строк матрицы B должны быть перемешаны попарно. 

• Следующим шагом необходимо задать фактический размер матриц в регистрах. Это осуществляется путем инициализации структуры TileConfig и ее последующей загрузкой. Данные о фактическом размере матриц будут потом неявно использовать в процессе загрузки, умножения и сохранения матриц.

• Далее загружаем сконвертированные матрицы в регистры, обнуляем аккумулятор и запускаем непосредственно саму операцию умножения.

• Далее выгружаем результат в основную память.

• Не забываем очистить файл конфигурации после использования.

После этого игрушечного примера посмотрим на реальную производительность AMX.

Теоретическая производительность матричного умножения

В начале протестируем чистую производительность AMX. Чтобы исключить влияние подсистемы памяти, будем предполагать, что все входные данные лежат в регистрах.

void PerfBf16L0(int count)
{
    for (int i = 0; i < count; i += 4)
    {
        _tile_dpbf16ps(0, 4, 6);
        _tile_dpbf16ps(1, 4, 7);
        _tile_dpbf16ps(2, 5, 6);
        _tile_dpbf16ps(3, 5, 7);
    }
}

Для чисел в формате bfloat16 скорость умножения двух матриц размером 32x16 занимает 16 процессорных тактов. Что составляет 3.7 TFLOPS для частоты 3.9 GHz. Это в 16 раз больше того, что можно достичь при использовании AVX-512 в формате float32.

void PerfInt8L0(int count)
{
    for (int i = 0; i < count; i += 4)
    {
        _tile_dpbuud(0, 4, 6);
        _tile_dpbuud(1, 4, 7);
        _tile_dpbuud(2, 5, 6);
        _tile_dpbuud(3, 5, 7);
    }
}

Для целых чисел в формате int8 скорость умножения двух матриц размером 64x16 составляет те же 16 тактов, что позволяет достичь 7.4 TOPS для частоты 3.9 GHz. Это в 8 раз больше, чем можно достичь при использовании AVX-512VNNI.

Отдельно отметим, что скорость умножения не зависит от фактического размера матриц, если приходится умножать матрицы меньшего размера, то на это все равно уходит 16 тактов. Кроме того тесты показывают, что в ядре есть фактически одно устройство матричного умножения, которое выполняет все операции умножения последовательно.

Практические ограничения

Конечно теоретически AMX обеспечивает 16 x 32 * 2 = 1024 операций bfloat16 за такт, однако практически нужно постоянно загружать в регистры исходные данные и выгружать из них результат, что будет сильно портить картину. Ну и кроме того, не забываем про необходимость конвертации исходных данных в формат bfloat16.

Если подходить к задаче в лоб, то для каждой операции матричного умножения C += A*B, требуется произвести 3 загрузки и одно сохранение, что приводит к к катастрофическому падению производительности из-за операций ввода/вывода.

В реальности обычно стараются часть регистров использовать в качестве аккумуляторов, что позволяет избежать постоянной загрузки и сохранения матрицы С.

Это в итоге сводит к необходимости 1 загрузки на одну операцию умножения матриц:

случае тактовой частоты в 3.9 GHz для достижения пиковой производительности в 3.7 TFLOPS необходима пропускная способность на уровне не менее 250 GB/s.

Далее протестируем скорость загрузки данных, и проверим хватит ли ее для обеспечения работы матричных регистров.

Скорость загрузки AMX регистров

В первом случае данные располагаются компактно:

void LoadCompact(int count, uint8_t* buf)
{
    for (int i = 0; i < count; i++)
        _tile_loadd(0, buf + i * 1024, 64);
}

В втором просто загружаем данные, лежащие построчно:

void LoadLongRows(int count, uint8_t* buf)
{
    for (int i = 0; i < count; i++)
        _tile_loadd(0, buf + i * 64, 64 * count);
}

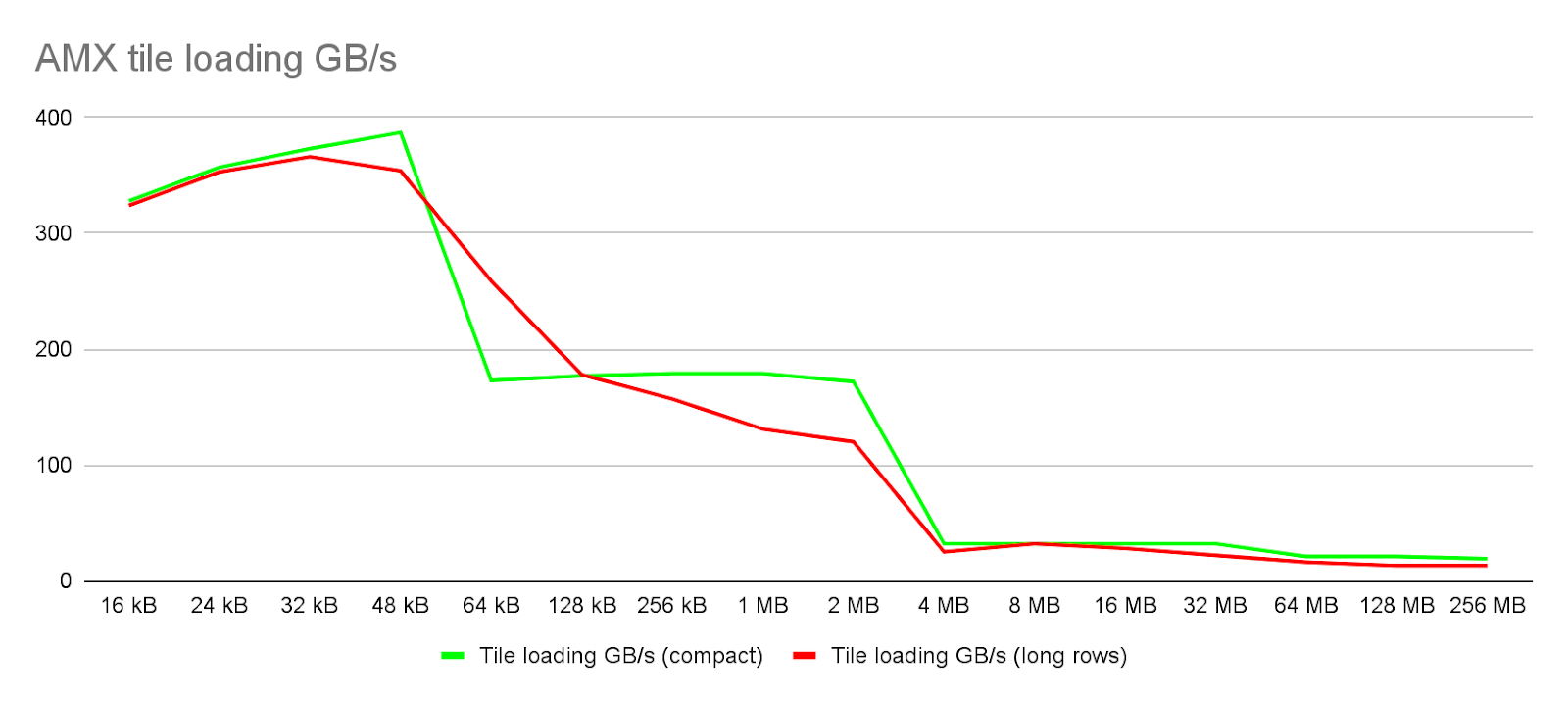
Как видно из данного графика, загрузка данных, которые лежат в L1 кэше (его размер составляет 48 kB) обеспечивает скорость загрузки вплоть до 380-390 GB/s что составляет где-то 75% от теоретического максимума. Этого теоретически достаточно для полной утилизации вычислительной способности матричного ускорителя. Однако, уже пропускной способности  L2 кэша (его размер составляет 2 MB) на уровне 170-180 GB/s (70% от теоретического максимума) не достаточно для полной утилизации матричного ускорителя. Пропускная способность L3 кэша составляет всего 32 GB/s, что лишь незначительно  превышает однопоточную пропускную способность памяти в 20-21 GB/s. К тому же он имеет размер всего в 1.9 MB на ядро, что даже меньше размера кэша L2. 

Данные ограничения пропускной способности, естественным образом сказываются на общей производительности, что наглядно может продемонстрировать следующий тест:

void PerfBf16L1(int count, uint8_t* buf, bool update, bool save)
{
    uint8_t* A0 = buf + 4 * 1024, *A1 = A0 + count * 1024;
    uint8_t* B0 = A1 + count * 1024, *B1 = B0 + count * 1024;
    if (update)
    {
        _tile_stream_loadd(0, buf + 0 * 1024, 64);
        _tile_stream_loadd(1, buf + 1 * 1024, 64);
        _tile_stream_loadd(2, buf + 2 * 1024, 64);
        _tile_stream_loadd(3, buf + 3 * 1024, 64);
    }
    else
    {
        _tile_zero(0);
        _tile_zero(1);
        _tile_zero(2);
        _tile_zero(3);
    }
    for (int i = 0; i < count; i++)
    {
        _tile_loadd(4, A0 + i * 1024, 64);
        _tile_loadd(5, A1 + i * 1024, 64);
        _tile_loadd(6, B0 + i * 1024, 64);
        _tile_loadd(7, B1 + i * 1024, 64);
        _tile_dpbf16ps(0, 4, 6);
        _tile_dpbf16ps(1, 4, 7);
        _tile_dpbf16ps(2, 5, 6);
        _tile_dpbf16ps(3, 5, 7);
    }
    if (save)
    {
        _tile_stored(0, buf + 0 * 1024, 64);
        _tile_stored(1, buf + 1 * 1024, 64);
        _tile_stored(2, buf + 2 * 1024, 64);
        _tile_stored(3, buf + 3 * 1024, 64);
    }
}

По сути это тест представляет собой упрощенное микроядро , от реального алгоритма перемножения матриц. C[32] *= A[32][K] * B[K][32] - перемножение блока строк на блок столбцов. Для наглядности приведем схему: 

Ниже на графиках приведены реально достижимые показатели производительности на уровне микроядра:

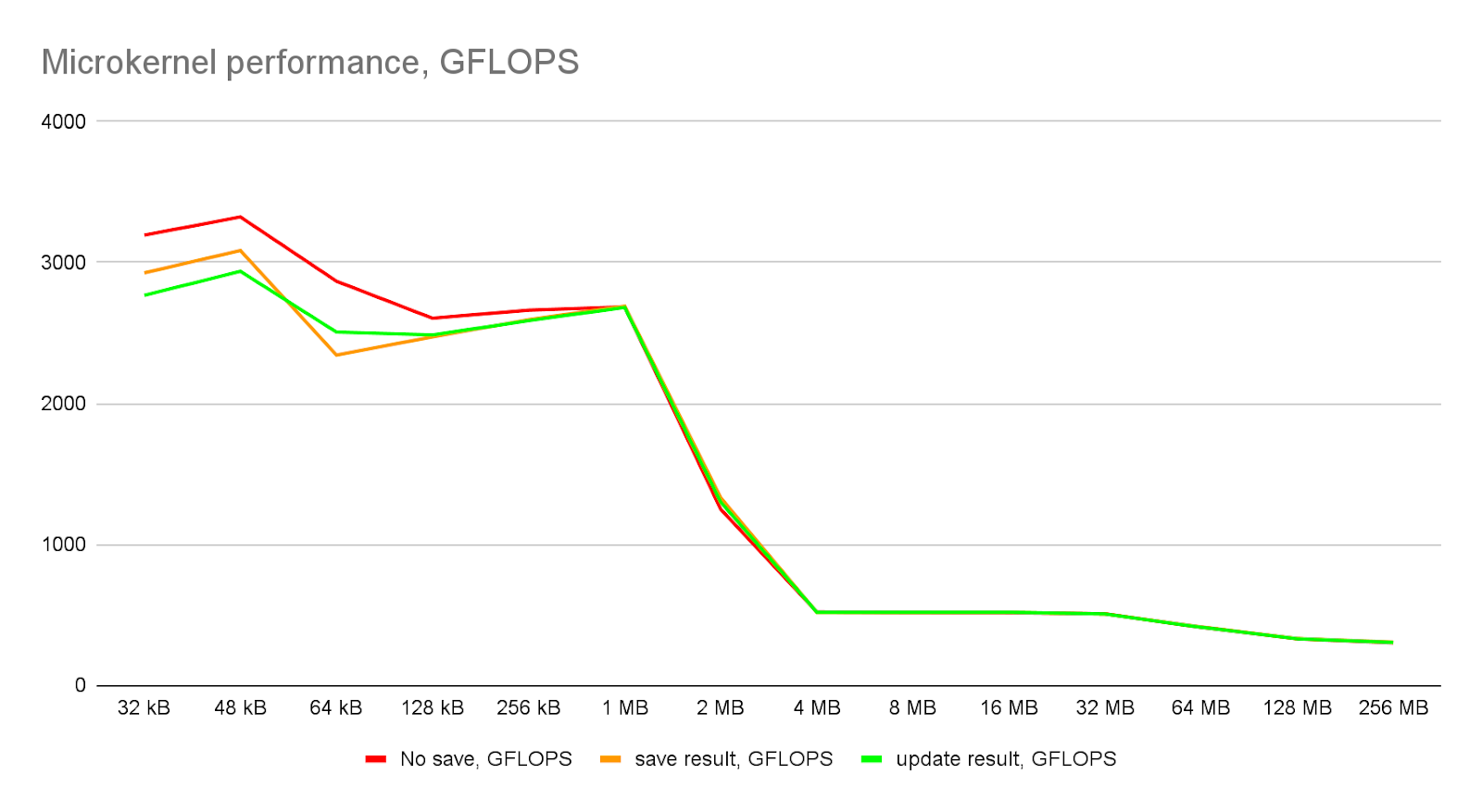
Видно, что в идеальных условиях, когда все данные лежат в L1 кэше, производительность может достигать 3.3 TFLOPS, что составляет 90% от теоретического максимума. Если учесть то, что результаты нужно куда то сохранять, то более реальным выглядит величина 2.9 - 3.0 TFLOPS (80% эффективность).

При локализации данных в  L2 кэше, производительность может достигать величины в 2.6 - 2.7 TFLOPS, что составляет порядка 70% от максимально возможной и очень хорошо согласуется с реальной пропускной способностью  L2 кэша, которую мы измерили ранее. Далее, если данные не локализуются в L1 или L2 кэше, то происходит драматическое падение производительности. Следовательно, любой эффективный алгоритм, который использует AMX, должен крутится вокруг локализации рабочих данных в пределах 2 MB.

Умножение матриц

Ну и простейшим алгоритмов, в таком случае будет умножение матриц. Попробуем его реализовать при помощи AMX. Сразу скажу, что пример упрощенный, в нем предполагается, что размер всех матриц кратен 32. 

Для начала реализуем микроядро:

void GemmMicro(int K, const uint16_t* A0, const uint16_t* A1,
    const uint16_t* B0, const uint16_t* B1,
    float* C, int ldc, bool update)
{
    if (update)
    {
        _tile_stream_loadd(0, C, ldc * 4);
        _tile_stream_loadd(1, C + 16, ldc * 4);
        _tile_stream_loadd(2, C + 16 * ldc, ldc * 4);
        _tile_stream_loadd(3, C + 16 * ldc + 16, ldc * 4);
    }
    else
    {
        _tile_zero(0);
        _tile_zero(1);
        _tile_zero(2);
        _tile_zero(3);
    }
    for (int k = 0; k < K; k += 32)
    {
        _tile_stream_loadd(4, A0 + k * 16, 64);
        _tile_stream_loadd(5, A1 + k * 16, 64);
        _tile_loadd(6, B0 + k * 16, 64);
        _tile_loadd(7, B1 + k * 16, 64);
        _tile_dpbf16ps(0, 4, 6);
        _tile_dpbf16ps(1, 4, 7);
        _tile_dpbf16ps(2, 5, 6);
        _tile_dpbf16ps(3, 5, 7);
    }
    _tile_stored(0, C, ldc * 4);
    _tile_stored(1, C + 16, ldc * 4);
    _tile_stored(2, C + 16 * ldc, ldc * 4);
    _tile_stored(3, C + 16 * ldc + 16, ldc * 4);
}

Здесь мы подгружаем данные матрицы B из двух квази столбцов (блоков по 16 столбцов), локализованных в L1 кэше. Данные матрицы A грузим из квази строк (блоков из 16 строк), которые должны быть локализованы в кэше L2. Для чего используем специальную инструкцию _tile_stream_loadd - которая загружает данные напрямую, минуя кэши верхнего уровня (чтобы не вытеснить из  L1 данные матрицы B). Аналогично при необходимости загружаются значения матрицы С. 

Далее сделаем макро ядро:

void ConvertA(int K, const float* A, int lda, uint16_t* buf)
{
    for (int k = 0; k < K; k += 32, A += 32)
        for (int i = 0; i < 16; ++i, buf += 32)
            ConvertA(A + i * lda, buf);
}

void ConvertB(int K, const float* B, int ldb, uint16_t* buf)
{
    for (int k = 0; k < K; k += 2, B += 2 * ldb, buf += 32)
        ConvertB(B, ldb, buf);
}

void GemmMacro(int M, int N, int K,
    const float* A, int lda, uint16_t* bufA,
    const float* B, int ldb, uint16_t* bufB,
    int convertB, float* C, int ldc, bool update)
{
    uint64_t n = 0;
    for (int j = 0; j < N; j += 32)
    {
        uint16_t* B0 = bufB + j * K;
        uint16_t* B1 = bufB + (j + 16) * K;
        if (convertB)
        {
            ConvertB(K, B + j + 0, ldb, B0);
            ConvertB(K, B + j + 16, ldb, B1);
        }
        for (int i = 0; i < M; i += 32)
        {
            uint16_t* A0 = bufA + i * K;
            uint16_t* A1 = bufA + (i + 16) * K;
            if (j == 0)
            {
                ConvertA(K, A + i * lda, lda, A0);
                ConvertA(K, A + (i + 16) * lda, lda, A1);
            }
            GemmMicro(K, A0, A1, B0, B1, C + i * ldc + j, ldc, update);
        }
    }
}

Данные, которые использует данная функция локализованы в кэше 2-3 уровня. При необходимости они подгружаются из памяти (заодно выполняется конверсия из float32 в bfloat16  для матрицы A и также переупорядочивание для матрицы B).

Ну и наконец, сама функция матричного умножения:

void GemmFunc(int M, int N, int K, const float* A, const float* B, float* C)
{
    TileConfig conf = {};
    conf.paletteId = 1;
    for (size_t i = 0; i < 8; ++i)
    {
        conf.rows[i] = 16;
        conf.colsb[i] = 64;
    }
    _tile_loadconfig(&conf);

    const int L1 = 48 * 1024, L2 = 2 * 1024 * 1024, L3 = 45 * 1024 * 1024;
    int mK = std::min(L1 / 2 / 32, K) / 32 * 32;
    int mM = std::min(int(L2 * 0.5) / 2 / mK, M) / 32 * 32;
    int mN = std::min(int(L3 * 0.1) / 2 / mK, N) / 32 * 32;
    std::vector<uint16_t> bufA(mK * mM), bufB(mN * mK);
    for (int j = 0; j < N; j += mN)
    {
        int dN = std::min(N, j + mN) - j;
        for (int k = 0; k < K; k += mK)
        {
            int dK = std::min(K, k + mK) - k;
            for (int i = 0; i < M; i += mM)
            {
                int dM = std::min(M, i + mM) - i;
                GemmMacro(dM, dN, dK,
                    A + i * K + k, K, bufA.data(),
                    B + k * N + j, N, bufB.data(), i == 0,
                    C + i * N + j, N, k != 0);
            }
        }
    }
    _tile_release();
}

В начале конфигурируем все регистры на максимальный размер. Далее выделяем два буфера под хранение блоков матриц A и B с данными подготовленными для AMX. 

Ниже приведена схема для лучшего понимания порядка, в котором происходит обход данных: 

Размер блока A - выбираем в 50% от L2 кэша, B - 10% от общего L3 кэша. Почему L2 кэш получается эффективно использовать только на половину? Видимо по тому, что он достаточно активно засоряется не используемыми данными матриц B и С. Как с этим бороться, я пока не нашел ответа. С использованием L3 кэша - здесь при текущей реализации алгоритма  больший процент не дает никакого ускорения.

Результат виден на графике ниже: 

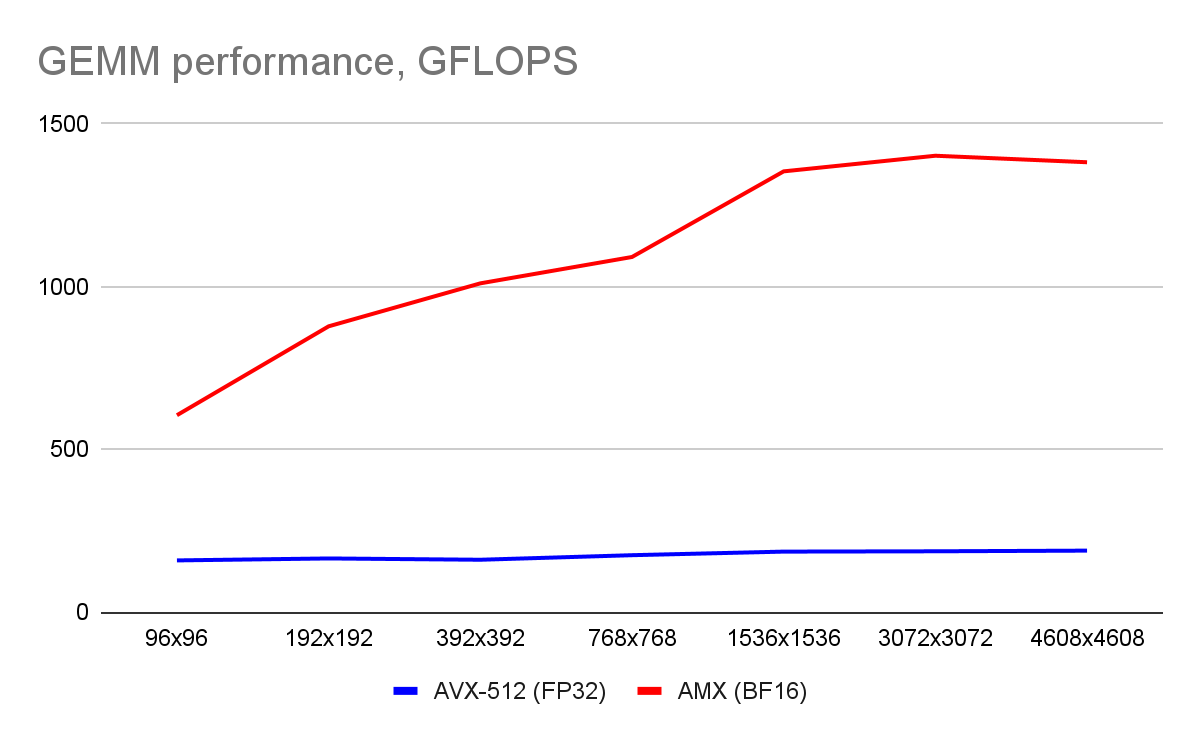
Видно, что производительность AMX на перемножении матриц достигает 1.4 TFLOPS, что составляет где-то 37% от теоретического максимума. Это с одной стороны вроде достаточно скромно, с другой стороны это в 7.5 раз быстрее, чем на AVX-512.

Причины низкой эффективности

Если кратко - AMX слишком быстрый для текущего размера кэша L1-L2 и пропускной способности L3 и основной памяти. В серии процессоров Xeon Max со встроенной высокоскоростной памятью HBM, эти проблемы в значительной мере устранены, однако проверить лично я этого пока к сожалению не могу. Лишь для Xeon Max AMX может раскрыть свой потенциал, однако эти процессора редки, да и ценник на них не совсем гуманный, мягко говоря. 

Что еще можно сделать

Если касаться возможности повышения производительности на текущем оборудовании, то для типичного применения AMX - инференса нейронной сети можно предложить следующее:

1. Заранее конвертировать и переупорядочить данные. По крайней мере для весов это всегда можно сделать. Это даст выигрыш как в отсутствие конверсии, так и в уменьшении нагрузки на подсистему памяти. 

2. Для сверток 2x2, 3x3, и т.д. возможно более компактное расположение данных, что позволяет сделать над ними больший объем вычислений, что по идее должно увеличить степень утилизации AMX.

Выводы

Если вы вдруг запускаете нейросети на CPU, то использование AMX - это то что доктор прописал. Да пусть не удастся задействовать всю его мощь целиком, но даже то, что реально достижимо вполне впечатляет (ускорение 7.5 раз на дороге не валяется). Да придется повозиться и естественно в среднем ускорение будет значительно скромнее, но оно все равно будет кратным для большого класса моделей. В данной статье я оставил за кадром вопросы многопоточности и тестирования на реальных задачах, возможно это будет заделом для будущих статей.