Привет, Хабр! В прошлой статье я указал, что в A/B-тестах используются три основных типа метрик, а именно пользовательские конверсии, средние метрики пользователей и ratio-метрики. К последним обычно относят средний чек, CTR баннера, среднюю длину сессии и др. Такие метрики имеют ограничения при оценке стандартными статистическими критериями и общую особенность определения в контексте экспериментов.

В этой статье формализуем понятие ratio-метрики, подробнее и на примере посмотрим на их ограничения и разберем, как инвалидировать результаты своих экспериментов, если эти ограничения игнорировать. Откроем для себя метод линеаризации ratio-метрик, разберем, как и почему он работает, какая интерпретация стоит за его преобразованием, а также определим его преимущества в сравнении с предусредненным средним, бутстрапом и дельта-методом.

❗Основная идея❗

Линеаризация позволяет перейти от ratio-метрики с зависимыми наблюдениями к средней пользовательской метрике с независимыми наблюдениями. При этом:

• В экспериментах разница линеаризованных метрик сохраняет сонаправленность наблюдаемого изменения с изменением в целевой ratio-метрике;

• Уровень статзначимости наблюдаемого эффекта новой метрики консистентен уровню статзначимости исходной ratio-метрики и рассчитывается t-тестом;

• К линеаризованной метрике можно применять методы повышения чувствительности, такие как CUPED или стратификация.

1. Формально про ratio-метрики

Введем два термина, а именно единица анализа и единица рандомизации.

Единица анализа — это сущность относительно которой мы хотим посчитать метрику. Ей может быть пользователь, сессия, заказ, кнопка, баннер, временной промежуток и тп.

К примеру, есть общий объем денег, полученный за какой-то период. Если мы его поделим (нормируем) на всех пользователей, то получим ARPU, а если на заказы — средний чек.

Также, можно сгруппировать данные по пользователям и для каждого определить его траты, построить их распределение, а средним значением этого распределения и будет ARPU. Проделав то же самое с заказами, в распределении их цен средним значением будет средний чек. Мы просто перераспределяем общий массив чего-то на какие-то различные единицы анализа.

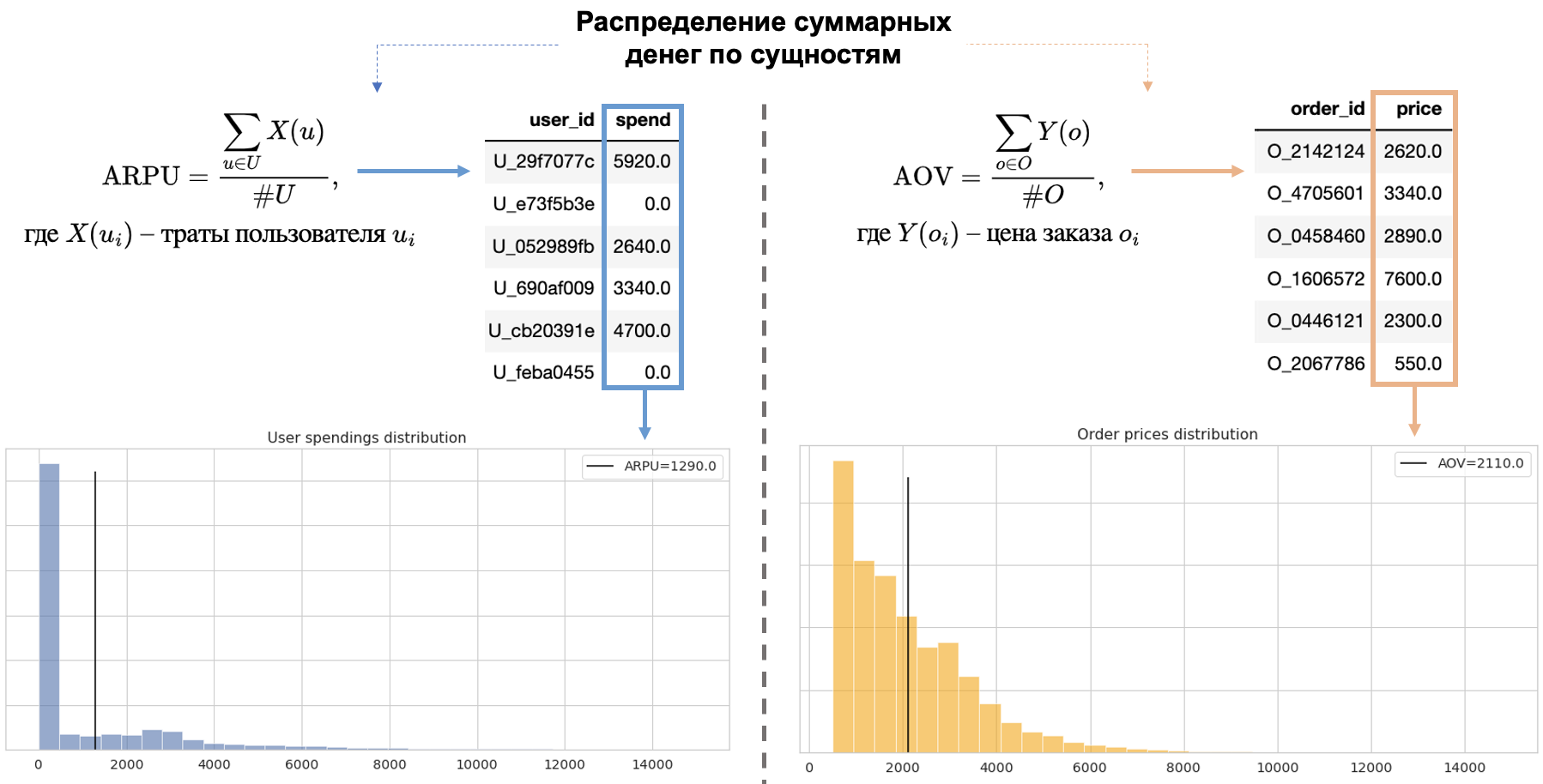
Единица рандомизации — это сущность, которую мы случайным образом назначаем в тестовую или контрольную группы в А/B-тестах, ей также может быть пользователь, сессия, заказ или временной промежуток. Но на практике чаще всего рандомизируют именно пользователей, на их примере и будем разбираться дальше.

Рандомизация помогает нивелировать влияние ненаблюдаемых факторов, которые могут исказить результаты эксперимента. К этим факторам можно отнести любой номинативный признак пользователя, например, возраст, пол, геолокацию, а также любой другой с менее четкой формулировкой — «излишне активный», «прокликивает только выгодные акции», «неуверенный/не знает что выбрать» и тп.

Благодаря рандомизации мы знаем, что наблюдаемая разница между значениями метрик в группах возникла в результате одного из двух вариантов:

• Либо из-за нашей экспериментальной механики;

• По чистой случайности, т.е. рандомное назначение в группы, возможно, привело к тому, что более результативные пользователи оказались в одной группе.

Кроме того, рандомизация обеспечивает независимость полученных от пользователей сигналов. Так, траты или клики одного пользователя не зависят от действий другого. Независимость наблюдений — одно из главных свойств для применения статистического критерия к данным.

Когда в эксперименте совпадает единица анализа и единица рандомизации, то смело можно применять статкритерий для проверки гипотезы. Это относится к любой пользовательской конверсии и средней пользовательской метрике, поскольку для одной метрики мы имеем только одну выборку независимых пользовательских сигналов.

Из-за требования статкритериев к независимости наблюдений все сигналы в A/B-тестах справедливо определять только в разрезе единицы рандомизации, т.е. пользователя.

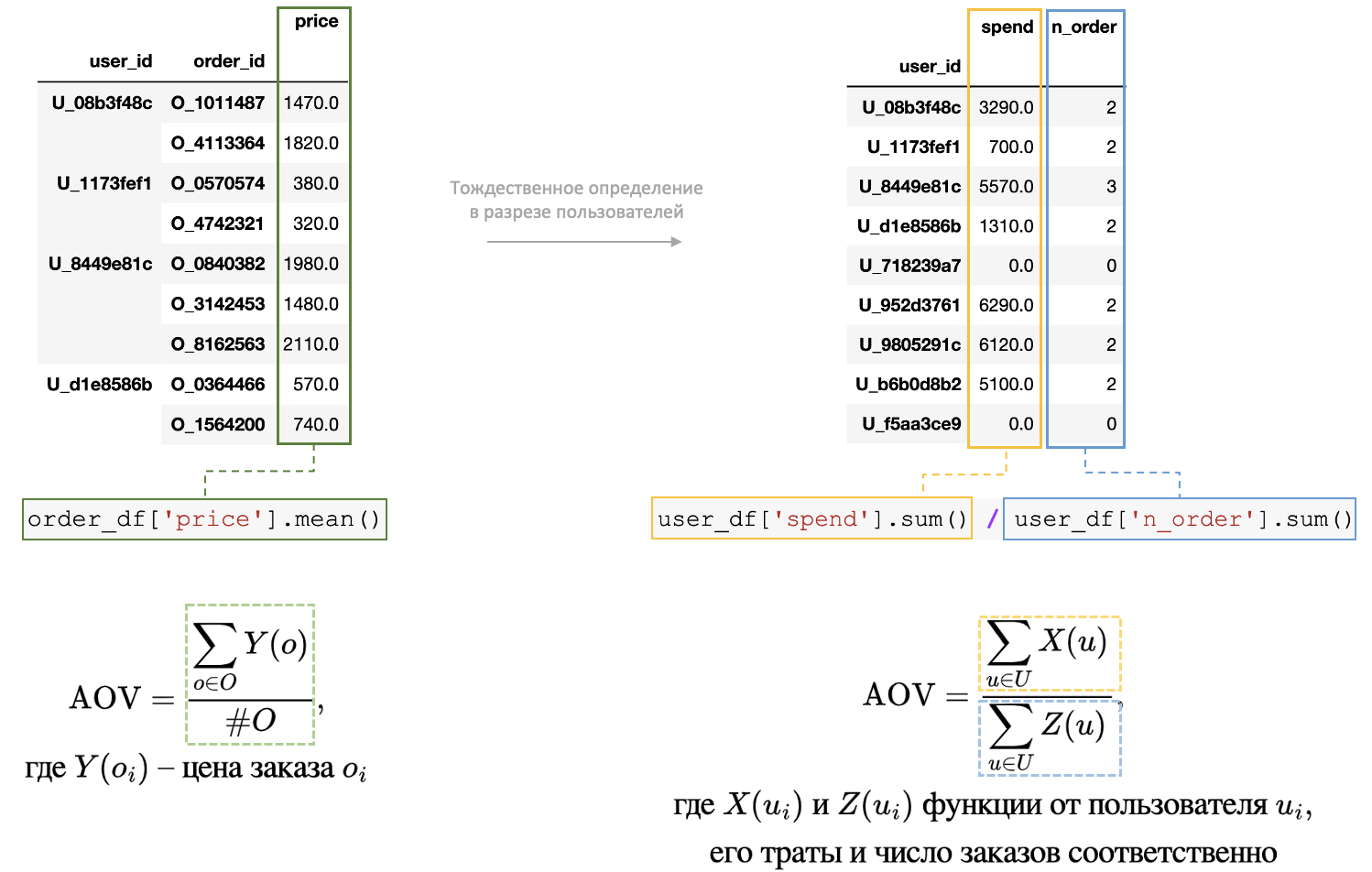
Когда в эксперименте хочется посчитать метрику относительно другой единицы анализа, отличной от единицы рандомизации, то появляется ratio-метрика, которая имеет особенность в формальном определении через единицу рандомизации.
Интересующая в эксперименте единица анализа всегда находится в зависимости от единицы рандомизации. При этом сами зависимые сущности и их сигналы можно «свернуть» до двух соответствующих пользовательских сигналов. К примеру, если у пользователя есть три заказа с определенными ценами, то для этого пользователя нужно просто посчитать число заказов и суммарные траты по ним. Проделав так для всех пользователей, дальше можно сложить сигналы по двум новым полям и поделить их суммы друг на друга, так получится среднее значение для интересующей единицы анализа, в нашем случае — средний чек.

Ratio-метрика — это метрика отношения непользовательского уровня (non-user level metric) с зависимыми наблюдениям, но которая явным образом выражается через отношение сумм соответствующих пользовательских сигналов.

2. Почему нельзя считать ratio-метрики t-тестом?

Формально — из-за нарушения предпосылок о независимости наблюдений, поскольку цены заказов, длины сессий, конверсии показов в клик и тп. в рамках одного пользователя адекватно считать скоррелированными. Получается, что принадлежащие одному пользователю единицы анализа и значения их сигналов зависят от субъективных характеристик этого самого пользователя.

Неформально это тезис можно проверить на синтетических A/A-тестах, распределяя по разным группам пользователей, а статзначимость оценивая, например, по их заказам. При этом распределение p-value для ratio-метрики будет отличаться от равномерного. В свою очередь, распределение p-value для средней пользовательской метрики по таким же сигналам будет иметь корректное равномерное распределение.

def aa_testing(df, stat_test, n_trails=10_000, alpha=0.05):
    rng = np.random.default_rng()
    p_vals_ratio = []
    p_vals_avg = []
    
    users = df['user_id'].unique()
    
    # a/a simulations
    for _ in tqdm(range(n_trails)):
        usr_hits = np.where(rng.random(len(users)) < 0.5, 't', 'c')
        
        tmp_df = pd.DataFrame(data=usr_hits, index=users, columns=['group'])
        aa_df = tmp_df.merge(df, left_index=True, right_on='user_id')
        
        # for ratio metric
        ordr_price_df = aa_df.groupby(['group', 'order_id'], as_index=False).agg(price=('gmv', 'sum'))
        t_price = ordr_price_df[ordr_price_df.group == 't'].price.values
        c_price = ordr_price_df[ordr_price_df.group == 'c'].price.values
        p_vals_ratio.append(stat_test(t_price, c_price))
        
        # for user lvl metric
        usr_spend_df = aa_df.groupby(['group', 'user_id'], as_index=False).agg(spend=('gmv', 'sum'))
        t_spend = usr_spend_df[usr_spend_df.group == 't'].spend.values
        c_spend = usr_spend_df[usr_spend_df.group == 'c'].spend.values
        p_vals_avg.append(stat_test(t_spend, c_spend))    

    
    fpr_ratio = sum(np.array(p_vals_ratio) < alpha) / n_trails
    fpr_avg = sum(np.array(p_vals_avg) < alpha) / n_trails
    return p_vals_ratio, fpr_ratio, p_vals_avg, fpr_avg

def t_test(s1, s2):
    return stats.ttest_ind(s1, s2).pvalue

p_vals_ratio, fpr_ratio, p_vals_avg, fpr_avg = aa_testing(order_df, stat_test=t_test)

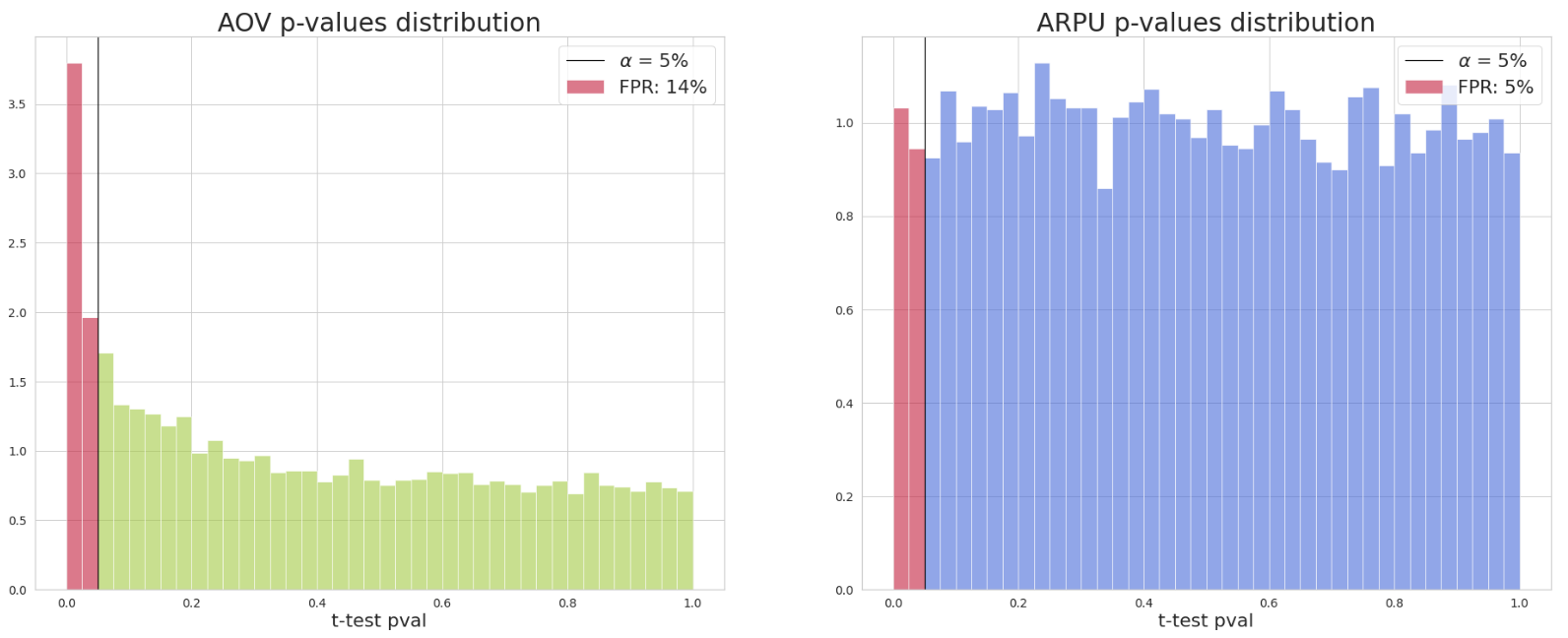
Получается, если расчитывать ratio-метрики t-тестом, то в ваших экспериментах будет расти ошибка 1-го рода, что приведет к значительному росту добавленных в продукт механик-пустышек без положительного влияния на бизнес.

Тогда встает логичный вопрос, а как в таком случае оценивать на статзначимость ratio-метрики, и здесь есть 3 распространенных варианта:

1. Посчитать через прокси-метрику, выраженную предусредненным средним значением на пользователя.

2. С помощью бутстрапа.

3. С помощью дельта-метода.

И каждый из них имеет свои недостатки. Давайте разбираться на примере среднего чека, CTR баннера и средней длины сессии.

3. Методы статистической оценки разницы ratio-метрик и их минусы

3.1. Предусредненное среднее

Наивное решение заключается в том, чтобы преобразовать ratio-метрику к средней пользовательской прокси-метрике, предварительно усреднив по пользователю соответствующие сигналы. Таким образом получится предусредненное среднее пользовательских значений. На картинке ниже указана общая формула для среднего чека на пользователя, CTR на пользователя и средней длины сессии на пользователя.

Для такой метрики корректно считать значимость стандартными статтестами, так как эти сигналы независимы. Однако у такой метрики есть проблема — в экспериментах наблюдаемый эффект в предусредненном среднем и в целевой ratio-метрике могут иметь разный знак, т.е. эффекты могут быть разнонаправлены. Например, средний чек на пользователя может статзначимо вырасти, но реальный глобальный средний чек мог упасть. Проверить это можно либо на корпусе проведенных экспериментов, либо с помощью симуляций.

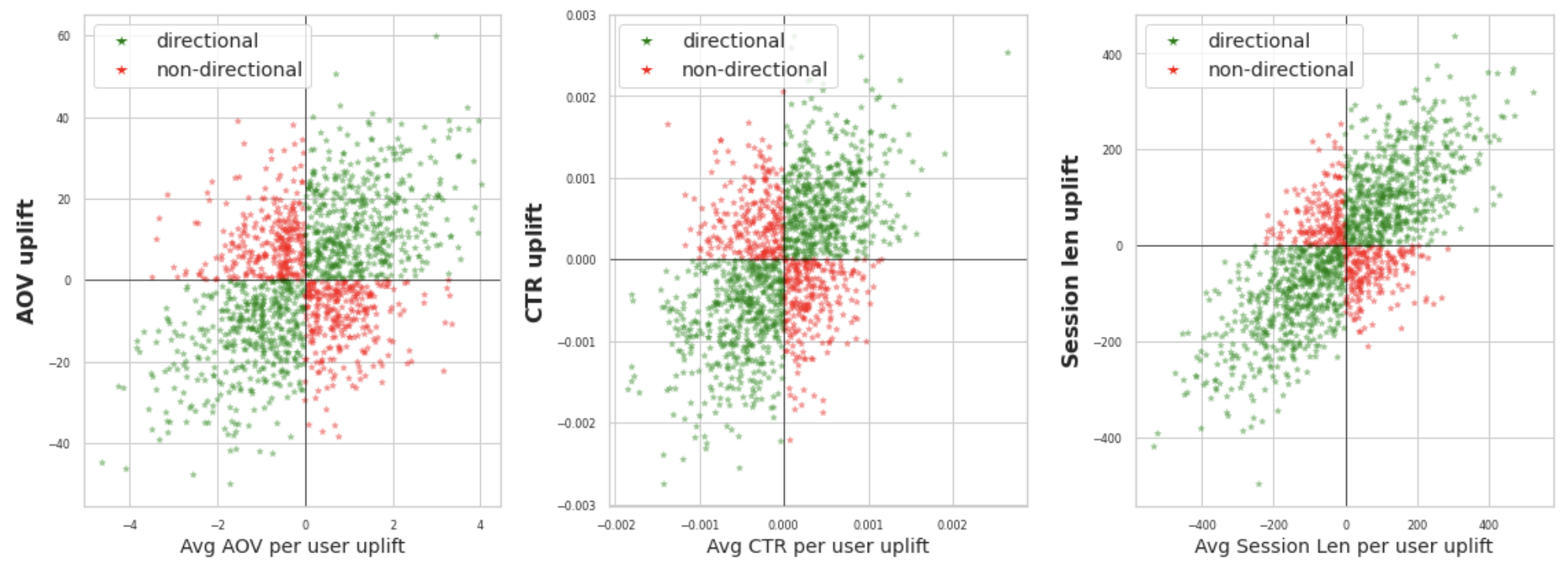
На картинке по оси Ox наблюдаемые изменения в предусредненном среднем, по Oy эффект в ratio-метрике. Сонаправленные изменения выделены зелеными точками, а разнонаправленные — красными. Получается из-за того, что в экспериментах может отсутствовать сонаправленность эффектов между этими метриками, то предусредненное среднее является плохой прокси-метрикой для замера статзначимости в ratio-метрике.

3.2. Бутстрап

Когда не знаешь как посчитать статзначимость для своей метрики — бутстрап в помощь.

Фактически проблема статоценки разницы ratio-метрик t-тестом связана с зависимостью наблюдений. Нельзя просто взять и по группам посчитать выборочную дисперсию и оценить стандартную ошибку среднего (standard error) для разницы ratio-метрик. А вот с помощью бутстрапа можно.

Для ratio-метрики надо семплировать с повторением случайных пользователей в группах и отбирать их соответствующие сигналы для числителя и знаменателя, считать разницу бутстрапированных ratio-метрик и повторять так много-много раз. По итогу получится эмпирическое распределение разницы ratio-метрик, среднем значением которого будет наблюдаемый эффект в эксперименте, с какой-то оценкой ее вариативности, эмпирической стандартной ошибкой среднего. Из этого распределения уже можно посчитать заветный p-value.

def to_np_array(*arrays):
    res = [np.array(arr, dtype='float') for arr in arrays]
    return res if len(res)>1 else res[0]


# num_t, num_c are arrays of user signals for numerator at groups
# denom_t, denom_c are arrays of user signals for denominator at groups
def bootstrap_ratio(num_t, denom_t, num_с, denom_c, n_trials=5_000):
    num_t, denom_t, num_с, denom_c = to_np_array(num_t, denom_t, num_с, denom_c)
    rng = np.random.default_rng()
    ratio_diff_distrib = []

    # booted iters
    for _ in range(n_trials):
        users_idx_t = rng.choice(np.arange(0, len(num_t)), size=len(num_t))
        boot_num_t = num_t[users_idx_t]
        boot_denom_t = denom_t[users_idx_t]
        ratio_t = boot_num_t.sum() / boot_denom_t.sum()

        users_idx_c = rng.choice(np.arange(0, len(num_с)), size=len(num_с))
        boot_num_с = num_с[users_idx_c]
        boot_denom_c = denom_c[users_idx_c]
        ratio_c = boot_num_с.sum() / boot_denom_c.sum()

        ratio_diff_distrib.append(ratio_t - ratio_c)
    
    # p_value
    mean = np.mean(ratio_diff_distrib)
    se = np.std(ratio_diff_distrib)
    quant = stats.norm.cdf(x=0, loc=mean, scale=se)
    p_value = quant * 2 if 0 < mean else (1 - quant) * 2
    
    return p_value
  

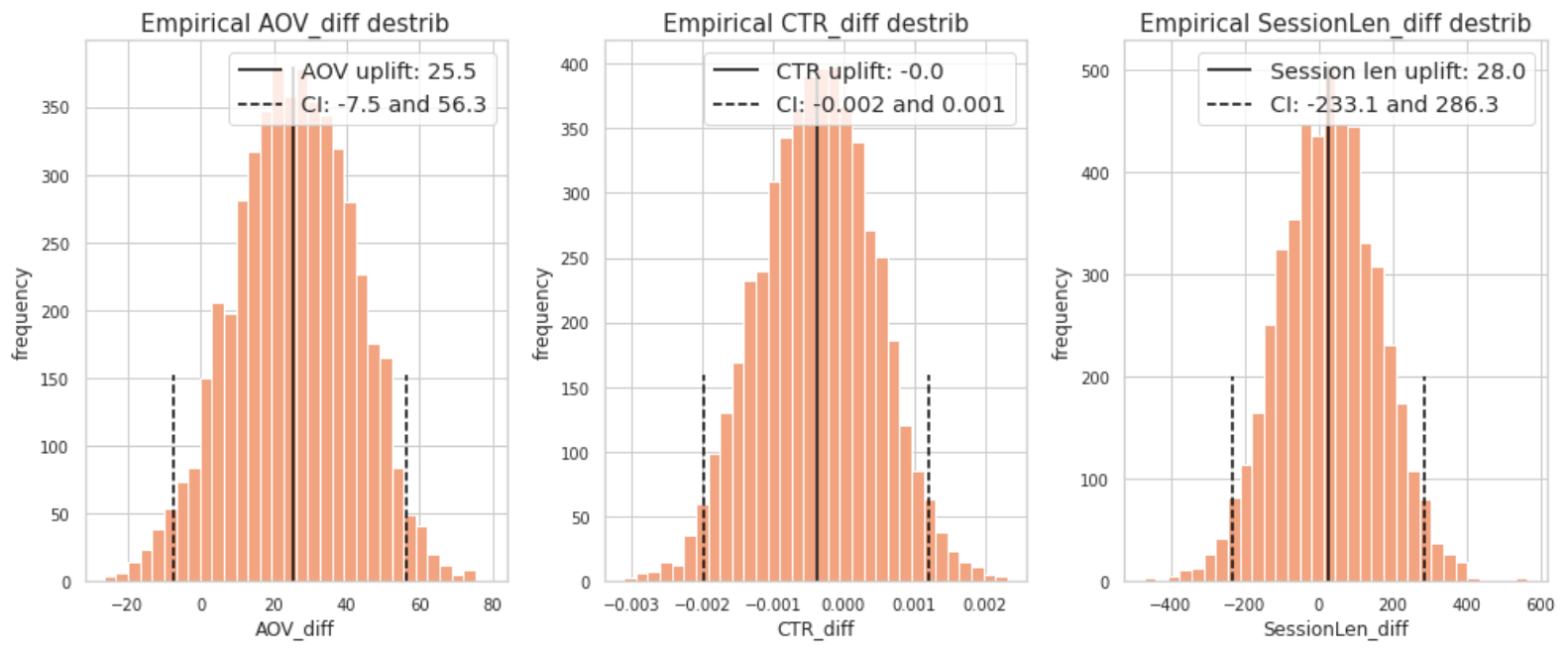
Бутстрап выдает корректные p-value для ratio-метрик, но минус подхода очевиден — бутстрап вычислительно затратен и не масштабируется в рамках платформы экспериментов, где могут считаться десятки ratio-метрик.

3.4. Дельта-метод

По своей сути дельта-метод делает тоже самое что и бустрап, но уже не эмпирически, а аналитически, через формулу. С помощью этой формулы можно корректно пересчитать дисперсию для ratio-метрик в тесте и контроле, а зная дисперсии и число пользователей в группах, уже можно оценить стандартную ошибку среднего для разницы ratio-метрик и соответственно t-статистику с p-value. Подробнее про дельта-метод в оригинальной статье или у коллег по цеху.

def to_np_array(*arrays):
    res = [np.array(arr, dtype='float') for arr in arrays]
    return res if len(res)>1 else res[0]


# num_t, num_c are arrays of user signals for numerator at groups
# denom_t, denom_c are arrays of user signals for denominator at groups
def delta_method(num_t, denom_t, num_c, denom_c):
    def est_ratio_var(num, denom):
        mean_num, mean_denom = np.mean(num), np.mean(denom)
        var_num, var_denom = np.var(num), np.var(denom)
        cov = np.cov(num, denom)[0, 1]
        # main formula for estimating variance of ratio-metric
        ratio_var = (
            (var_num / mean_denom**2)
            - (2 * (mean_num / mean_denom**3) * cov)
            + ((mean_num**2 / mean_denom**4) * var_denom)
        )
        return ratio_var
    
    num_t, denom_t, num_c, denom_c = to_np_array(num_t, denom_t, num_c, denom_c)
    
    ratio_t, ratio_c = num_t.sum()/denom_t.sum(), num_c.sum()/denom_c.sum()
    var_t, var_c = est_ratio_var(num_t, denom_t), est_ratio_var(num_c, denom_c)
    n_t, n_c = len(num_t), len(num_c)

    uplift = ratio_t - ratio_c
    se = np.sqrt(var_t/n_t + var_c/n_c)
    
    t = uplift / se
    p_value = (1 - stats.norm.cdf(abs(t))) * 2
    return p_value

Если считать статзначимость бутстрапом и дельта-методом на одинаковых выборках для разницы ratio-метрик, то p-value двух методов будут совпадать с достаточной точностью и иметь линейную зависимость с единичным угловым коэффициентом. Можно сказать, что значения p-value дельта-метода консистентны значениям, полученным с помощью бутстрапа. Соответственно, и на A/A-тестах дельта-метод дает равномерные распределения для ratio-метрик и не завышает ошибку 1-го рода.

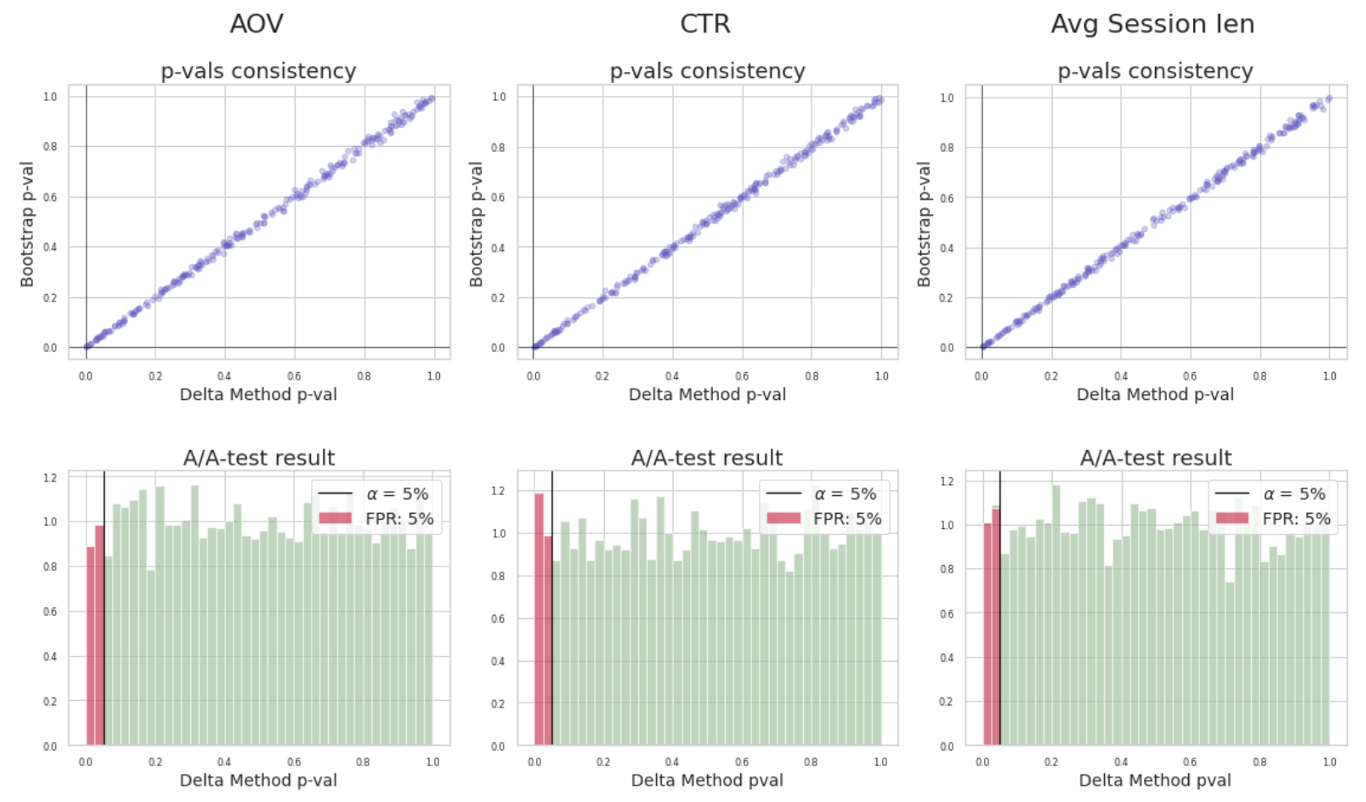
Недостатки у подхода тоже есть. Так как мы не работаем напрямую с пользовательскими сигналами, то для ratio-метрик не получится использовать методы повышения чувствительности, т.е. в экспериментах для пользовательских конверсий и средних пользовательских метрик можно применить CUPED, для ratio-метрик — нет.

Но есть один отличный метод, который лишен всех описанных выше недостатков.

4. Линеаризация

Определим функцию линеаризации двух пользовательских сигналов, чтобы для каждого пользователя получить один сигнал. Из этих новых сигналов соберем новую среднюю пользовательскую линеаризованную метрику, которая будет прокси к исходной ratio-метрике.

# at user_df user level signals with exp group info

is_cntrl = user_df.group=='c'

AOV_cntrl = user_df[is_cntrl].spend.sum() / user_df[is_cntrl].n_order.sum()
user_df['lin_aov'] = user_df.spend - AOV_cntrl * user_df.n_order

CTR_cntrl = user_df[is_cntrl].n_bnr_clkd.sum() / user_df[is_cntrl].n_bnr_vwd.sum()
user_df['lin_ctr'] = user_df.n_bnr_clkd - CTR_cntrl * user_df.n_bnr_vwd

def to_np_array(*arrays):
    res = [np.array(arr, dtype='float') for arr in arrays]
    return res if len(res)>1 else res[0]


# num_t, num_c are arrays of user signals for numerator at groups
# denom_t, denom_c are arrays of user signals for denominator at groups
def linearization(num_t, denom_t, num_c, denom_c):
    def lin(num, denom, cntrl_ratio):
        return num - cntrl_ratio * denom
    
    num_t, denom_t, num_c, denom_c = to_np_array(num_t, denom_t, num_c, denom_c)
    
    CNTRL_ratio = num_c.sum() / denom_c.sum()
    
    lin_signals_t = lin(num_t, denom_t, CNTRL_ratio)
    lin_signals_c = lin(num_c, denom_c, CNTRL_ratio)
    
    p_val = stats.ttest_ind(lin_signals_t, lin_signals_c).pvalue
    
    return p_val
  

А что за значения линеаризованных сигналов получились, как их воспринимать и как инерпритировать новую метрику?

К линеаризованным сигналам можно относиться как к единицам вклада в изменение ratio-метрики от начального значения в контроле до наблюдаемого в тесте. Этот тезис можно наглядно продемонстрировать на распределениях этих вкладов в экспериментальных группах.

Математическое ожидание линеаризованной метрики в контрольной группе всегда равняется нулю, т.е. суммарно в контроле вклада нет, так как относительно ratio-метрики в контроле и замеряем. В тестовой же группе будет какое-то другое среднее значение вкладов, либо положительное, либо отрицательное.

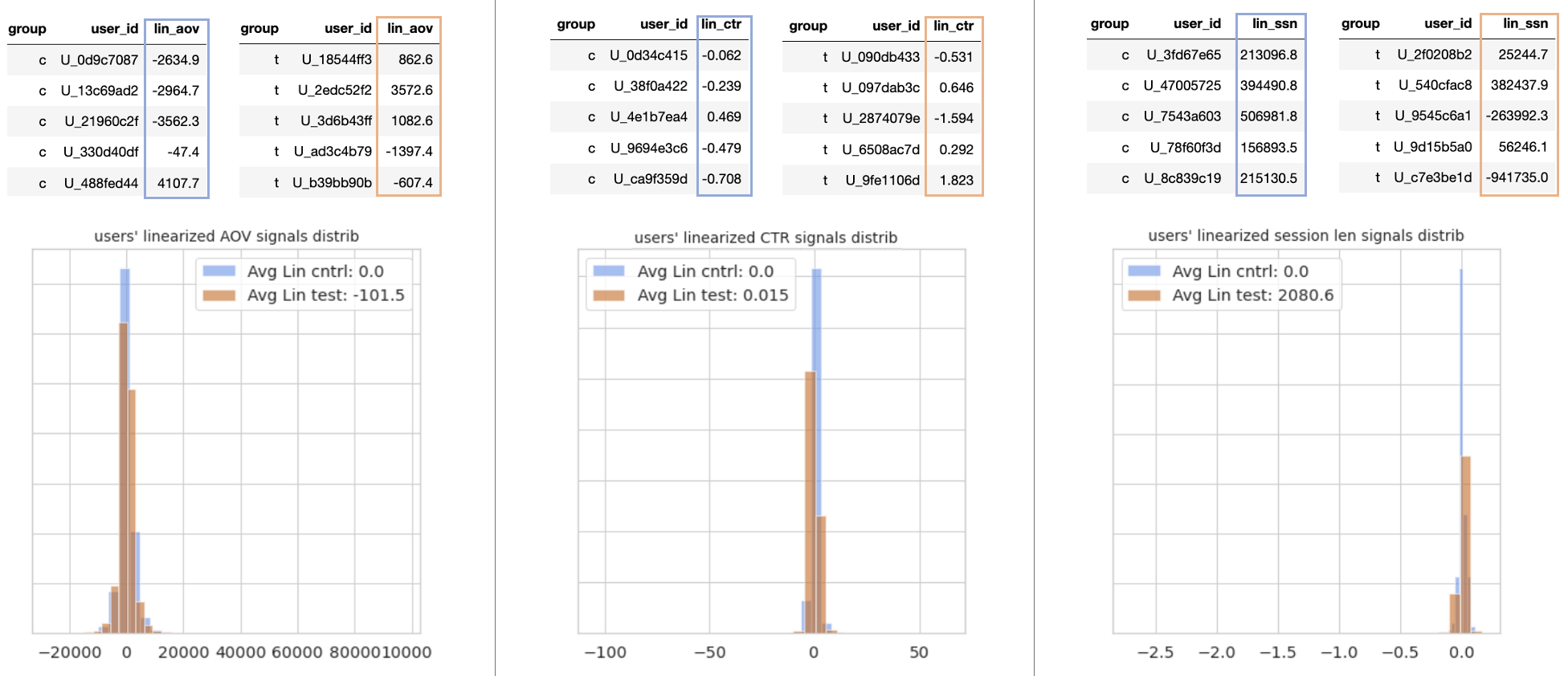
При этом линеаризованная метрика обладает рядом положительных особенностей.

Во первых, в отличии от предусредненного среднего, разница линеаризованных метрик всегда сохраняет сонаправленность с изменением в целевой ratio-метрике. Например, если в эксперименте CTR вырос или упал, то линеаризованный CTR всегда изменится в ту же сторону.

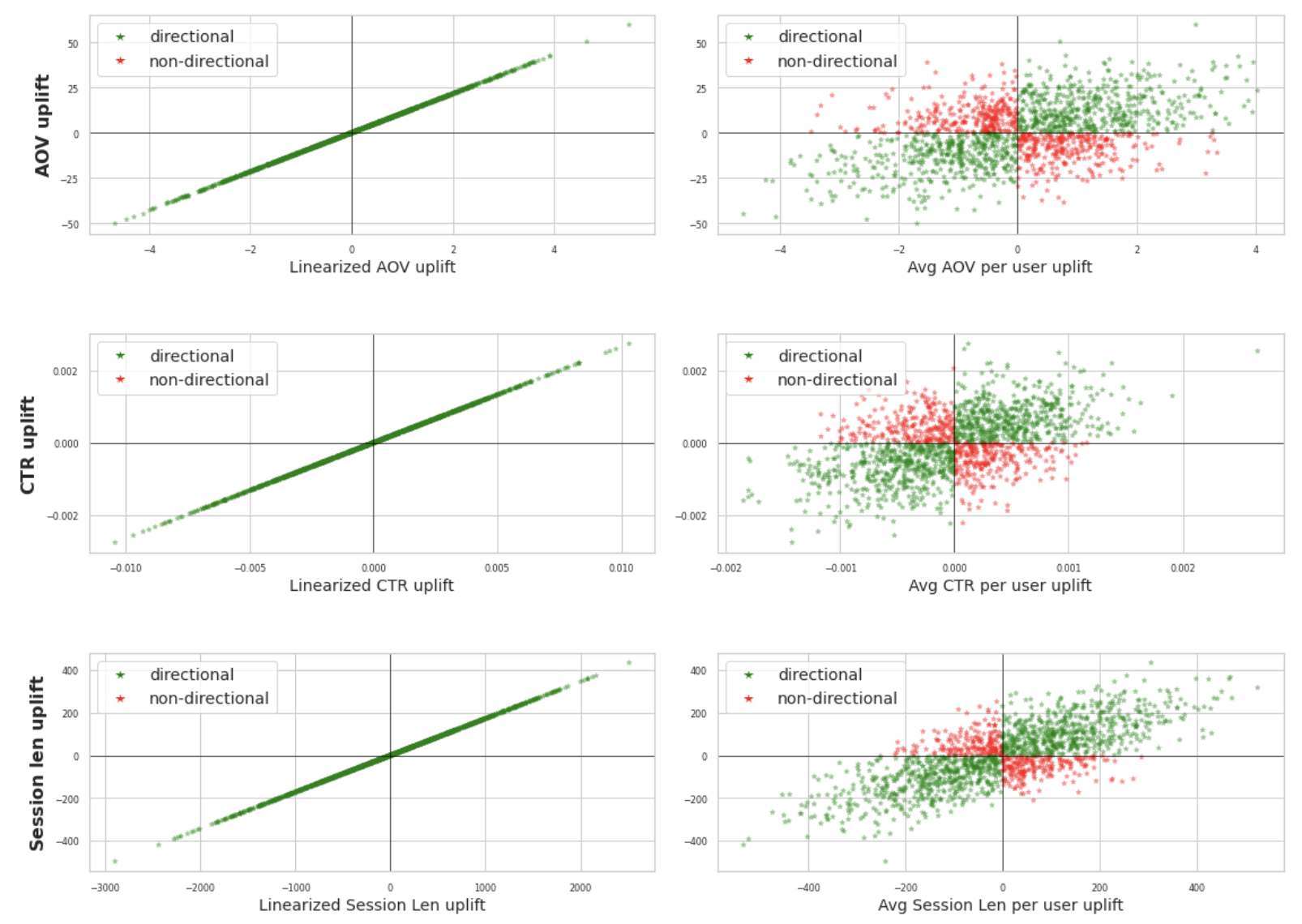
Во вторых, линеаризованные пользовательские сигналы уже можно считать независимыми и для них определять статзначимость t-тестом. При этом, значения p-value для линеаризованной метрики будут консистентны значениям, полученным с помощью дельта-метода на исходной ratio-метрике. Это значит, что дельта-метод можно заменить линеаризацией и получать одинаковые значения p-value с достаточной точностью. Соответственно и на А/А-тестах линеаризация показывает корректные результаты.

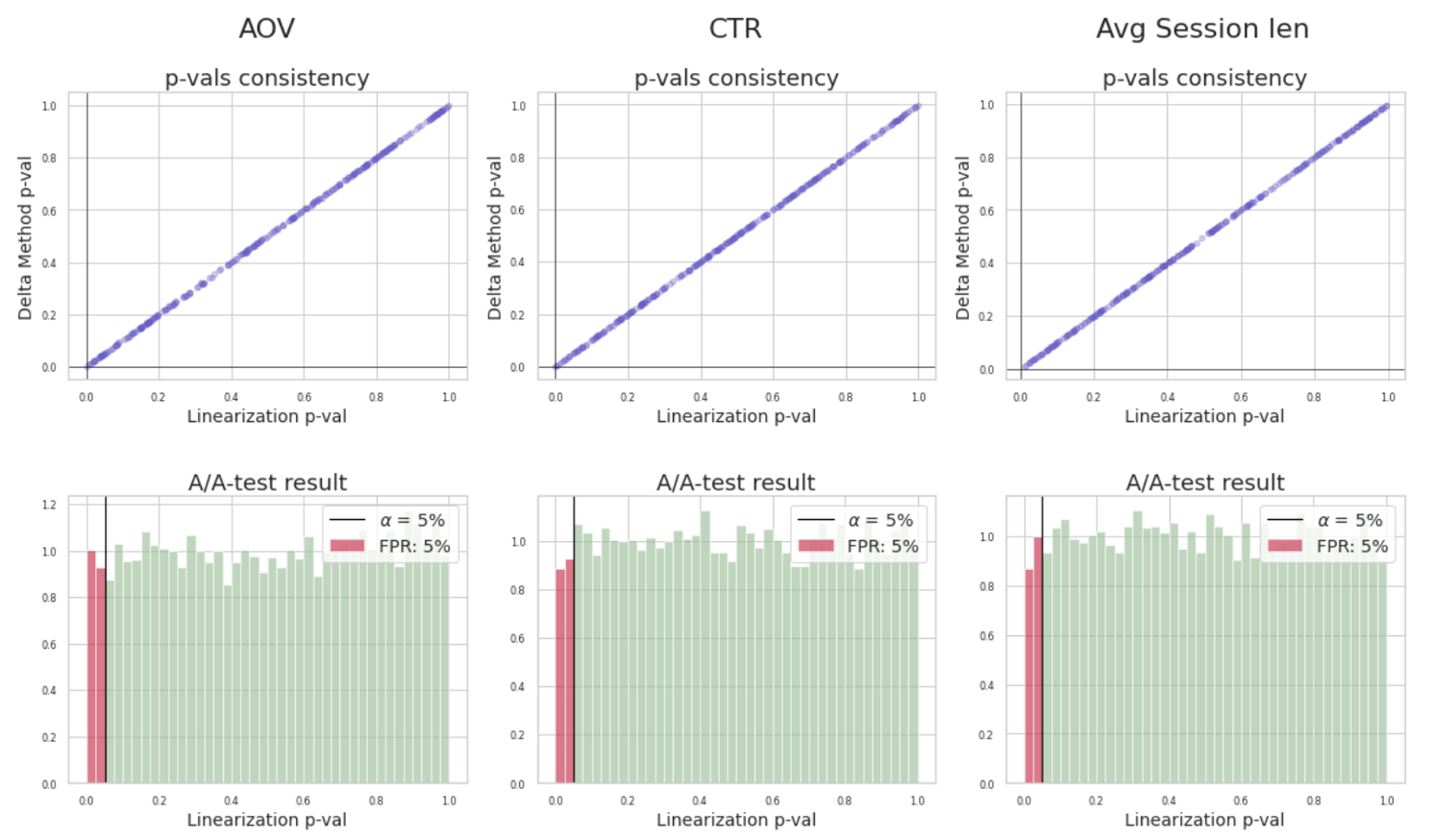
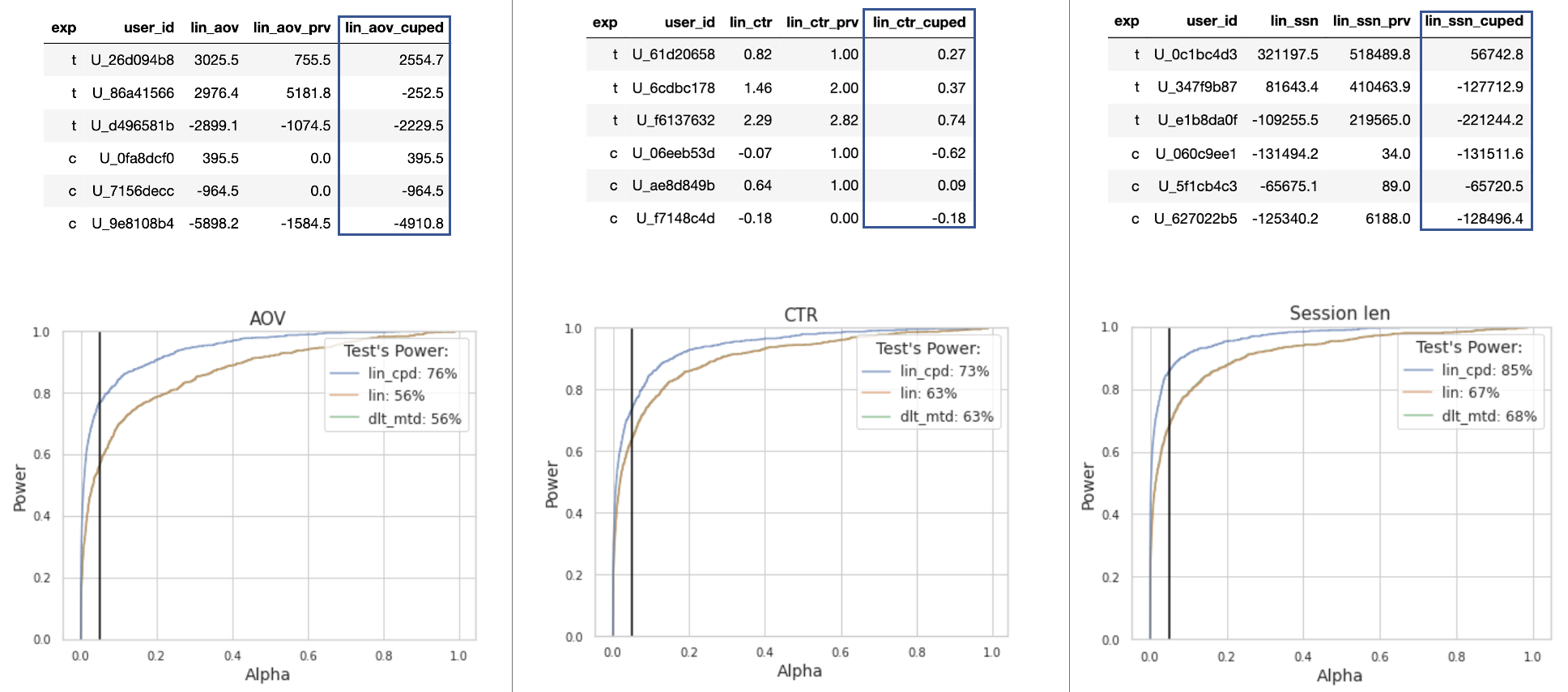
В третьих, линеаризация позволяет использовать методы повышения чувствительности на ratio-метриках, чтобы уменьшать размеры экспериментальных групп для обнаружения эффектов или чтобы увеличивать мощность в наблюдаемых результатах. Например, чтобы использовать CUPED для ratio-метрики, необходимо ее линеаризовать и линеаризовать соответствующие сигналы на предэкспериментальном периоде. Получатся две средние пользовательские метрики, к которым уже можно применить CUPED.

На картинке внизу видно, что такой критерий оказывается более мощным в сравнении с обычной линеаризацией и дельта-методом.

Вывод

Линеаризация в A/B-тестах легко вычисляемый и отлично масштабируемый метод трансформации ratio-метрики к средней пользовательской метрике. Она сохраняет сонаправленность наблюдаемого эффекта с изменением в целевой ratio-метрике. Также в экспериментах разница линеаризованных метрик имеет консистентный уровень статзначимости с исходной ratio-метрикой и рассчитывается t-тестом. Поскольку благодаря линеаризации мы получаем сигналы пользовательского уровня, то открываются возможности применять для ratio-метрики методы повышения чувствительности.

И именно линеаризация ratio-метрик с применением CUPED внедрена в нашу платформу A/B-тестов.

References

1. Оригинальная статья — Consistent Transformation of Ratio Metrics for Efficient Online Controlled Experiments;

2. Илья Кацев — Как измерить счастье пользователя;

3. Роман Будылин — Как делать чувствительные метрики для АБ-тестирования;

4. Виталий Полшков — Эффективное А/Б тестирование.