Если вы по кусочкам и фрагментарно изучаете разные аспекты и тонкости A/B-тестирования, но множество концепций и идей не ложатся в единую систему, то это статья для вас.

Предлагаю разобрать структуру A/B-тестов сверху вниз. Пройдем по основным этапам от наблюдаемой разницы в целевой метрике до матрицы ошибок. Формализуем, систематизируем и идейно свяжем те концепции, которые стоят за экспериментами. Постараемся сформировать цельное представление об этой процедуре, обозначим, что эксперименты делают, чего не делают, как делают, в каком представлении работают с данными и метриками.

❗Основная идея❗

Результаты A/B-тестов не показывают однозначно, стало ли что-то в продукте лучше или хуже. Статпроцедура, лежащая в основе экспериментов, контролирует уровень ошибки, ниже которого наблюдаемый эффект будет принят как нечто содержательное, хотя в действительности эффекта нет, а разница достигнута случайно.

Формально механика проведения A/B-тестов контролирует ошибку 1-го рода, что снижает долю релизнутых в продукт изменений без положительного влияния на бизнес.

Итак, немного продуктовой мотивации

Продукт создается и развивается, чтобы удовлетворять потребность пользователя. Пользователь просматривает баннеры, кликает по кнопкам, пролистывает ленту до разных позиций, оформляет заказы и тратит деньги. По сути, пользователь оставляет сигналы в продукте, которые детектируются и складываются в логи.

Чаще всего, центральная сущность, на которую направлены усилия в экспериментах и на поведение которой хочется влиять, —  пользователь. Стандартным объектом рандомизации, который мы случайным образом распределяем в тестовую или контрольную группы, выступает также пользователь. Соответственно, и метрики в A/B-тестах в этом случае определяются в разрезе пользователей.

1. Верхушка айсберга

1.1 Метрики

Продуктовая метрика в обобщенном смысле — это единственное число, агрегата над сигналами пользователей из некоторого множества U. При этом в большинстве случаев она выражается через пару функций от пользователей следующим образом:

Три частных случая продуктовых метрик определяются через формулу выше.

• Доли. Бинарные сигналы, например, конверсия в покупку или retention rate. Подразумевается, что пользователь, соответствующий определенному критерию, сделал какое-то действие. Т.е. в общем случае попал в некоторое подмножество S множества U:

•  Средние метрики пользователей. Численные сигналы, например, среднее число добавленных товаров в корзину на юзера или ARPU:

•  Ratio-метрики. Отношение двух сумм пользовательских сигналов, например, средний чек, средняя длина сессии или CTR:

Ratio-метрика — это метрика с зависимыми наблюдениям. Например, если в A/B-тесте сагрегировать сигналы по заказам, чтобы посчитать средний чек, то несколько заказов могут быть сделаны одним пользователем. Получается ratio-метрику еще можно определить через сигналы объектов, которые относятся к пользователям как N к 1 и значения которых в рамках одного пользователя можно считать скорелированными. Такие метрики нельзя оценивать стандартными статкритериями, которые требуют независимости наблюдений:

При дизайне новых метрик или чтобы отделять одну метрику от другой, удобно думать о том, на каких сигналах и с какого этапа продуктовой воронки они собираются.

1.2 Воронка

Модель продукта или отдельного продуктового направления хорошо воспринимается в виде воронки. Она позволяет описать путь пользователя через различные этапы, на которых пользователи оставляют сигналы, а продуктовые команды реализуют экспериментальные механики.

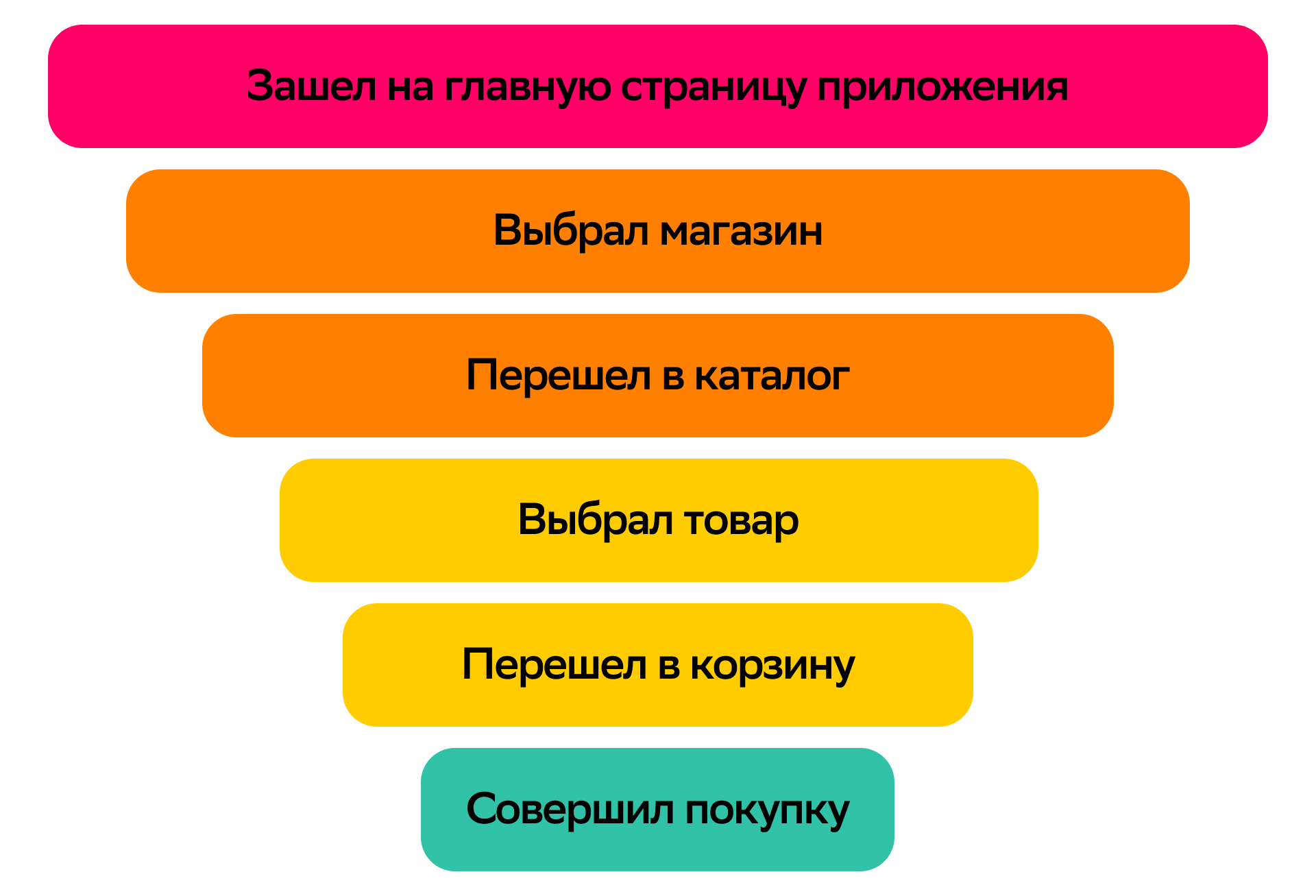
Метрики конверсий отражают движение пользователей вниз по воронке, указывая, сколько пользователей переходит с одного этапа на другой. Средние пользовательские метрики измеряют горизонтальную активность на отдельных этапах воронки, оценивая действия пользователей на одном и том же уровне.

Если за период всего эксперимента интересует не единственный факт перехода пользователей на следующий этап воронки, выраженный конверсией, а сколько раз они суммарно были на одном этапе и суммарно переходили на следующий, то это ratio-метрики. Такие метрики, в частности, отвечают на вопрос — как хорошо новый дизайн побуждает пользователей каждый раз переходить на следующий этап, т.е. сумма показов делится на сумму кликов-переходов.

При выборе приемочных метрик самыми чувствительными для обнаружения эффекта являются те, которые находятся на этапе воронки, где реализована экспериментальная механика. Эти метрики — индикаторы непосредственного изменения поведения пользователей от экспериментального воздействия. Например, если поменять дизайн кнопки в каталоге товаров, то число кликов на юзера или кликабельность кнопки будут более чувствительны, чем ARPU или средний чек. После того как пользователь увидит новый дизайн кнопки, ему придется пройти много этапов в приложении, чтобы сконвертироваться в итоговую трату денег, до которой он может и не дойти.

После агргеации сигналов по пользователям с различных этапов воронки получается датасет, ключом которого является пользователь. Для каждого известна группа и рассчитаны метрики, которые имеют распределения для соответствующих экспериментальных групп. С ними и погружаемся глубже на следующий уровень айсберга, где сигналы подвергаются преобразованиям.

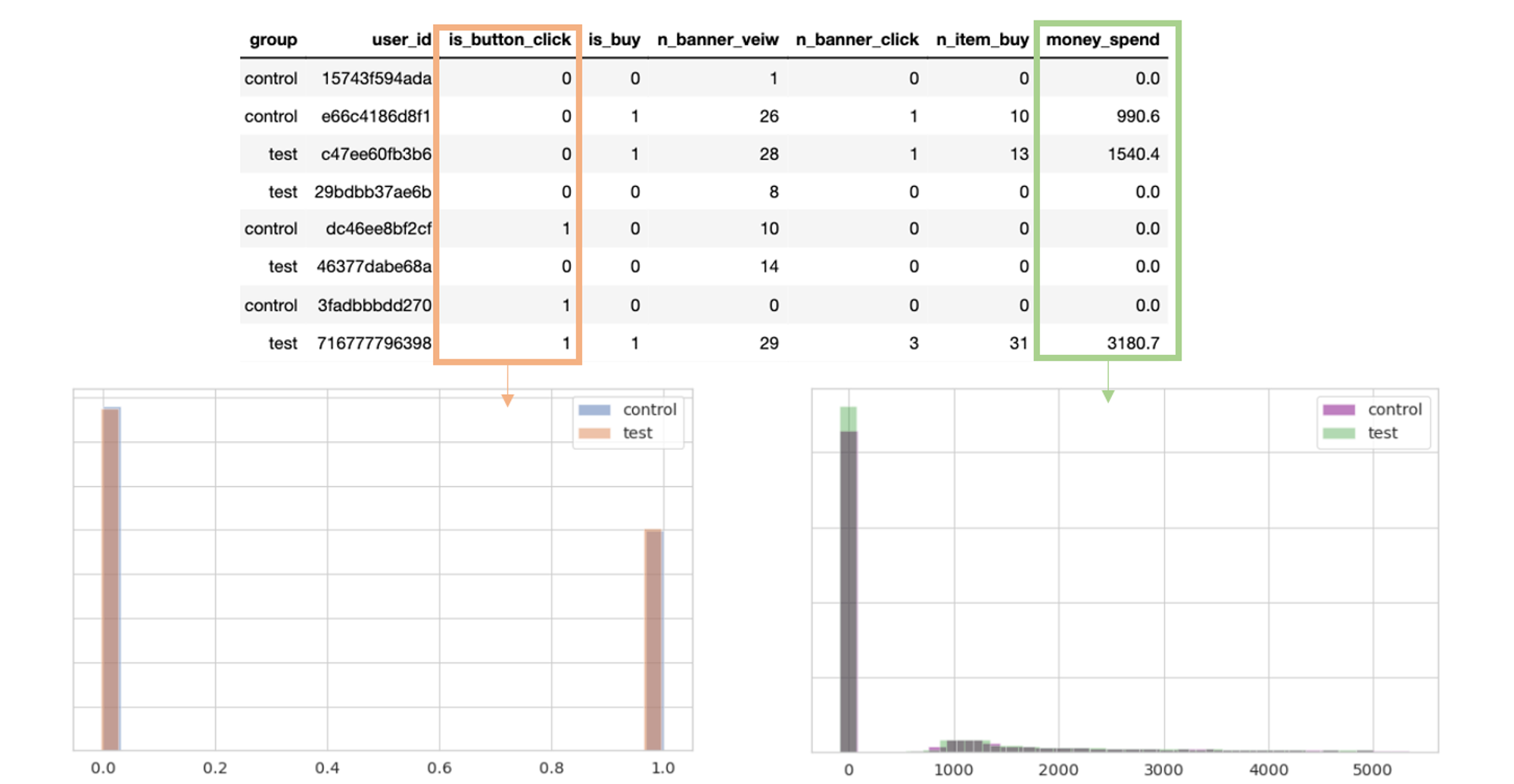
2. Там, где еще плавает рыба

Пользовательские сигналы можно преобразовывать модными методами для увеличения чувствительности метрик к обнаружению эффекта. К ним можно отнести CUPED, линеаризацию, стратификацию, бакетный метод и др. Каждый метод достоин отдельной подробной статьи, поэтому в этой укажу только мотивацию их применения.

Главная идея —  компенсация «изъянов» в полученных данных и ограничений в статпроцедуре:

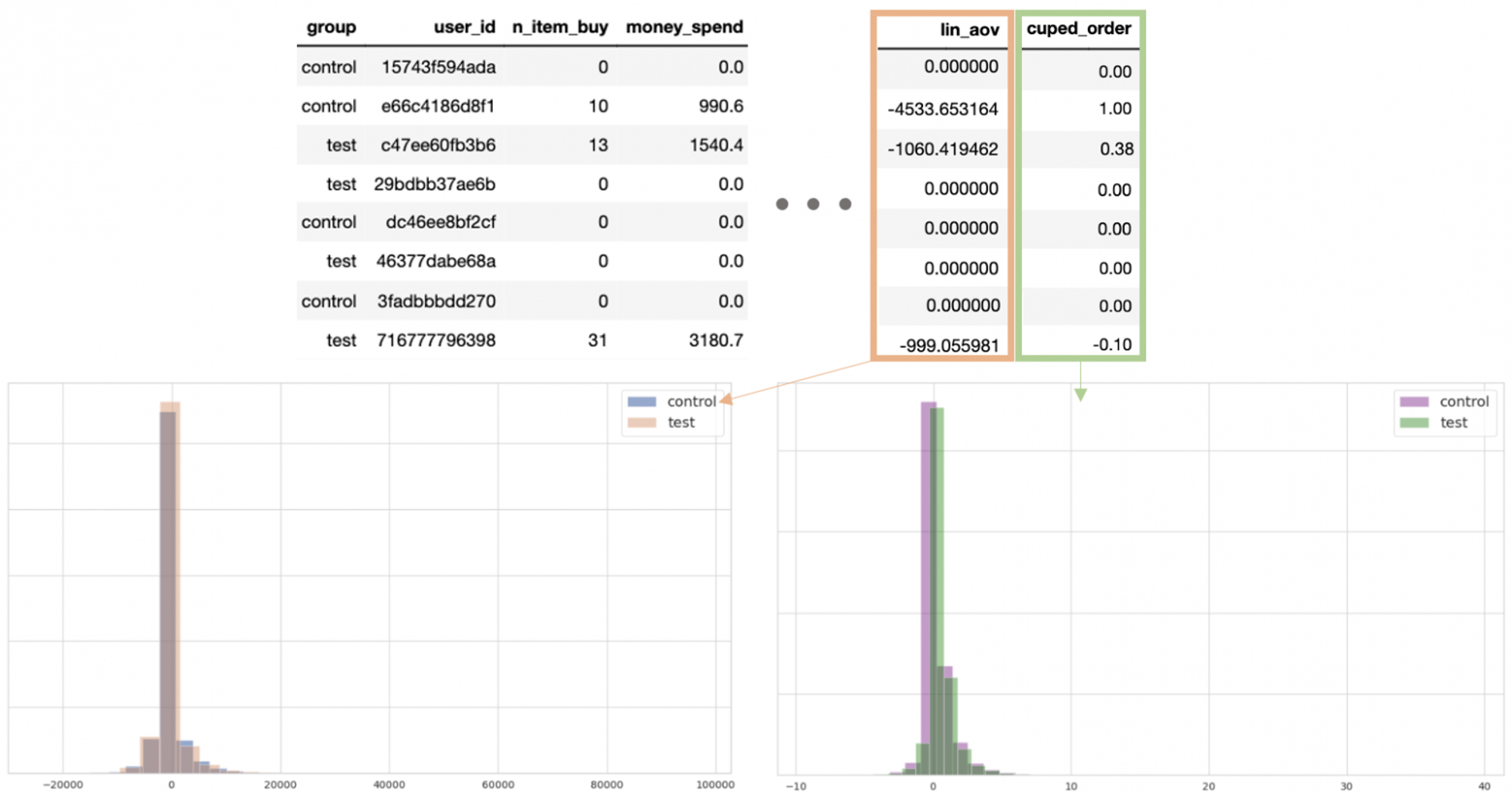
• Линеаризация преобразует ratio-метрику с зависимыми наблюдениями в среднюю поюзерную с независимыми, которую уже можно оценивать t-тестом.

• CUPED устраняет влияние предэкспериментального поведения пользователей на данные в текущем эксперименте. В том числе отчасти компенсирует смещение отбора (selection bias) в экспериментальные группы.

• Бакетный метод, как бутстрап для бедных, позволяет считать любые метрики. Он позволяет оценивать на статзначимость хоть ratio-метрики, хоть суммарные деньги в эксперименте, а не ARPU.

3. Бездна или тем, где утопают мальки

Получив значения метрик в тесте и контроле, почему бы не посмотреть на наблюдаемую разницу и заявить, что это — эффект от нашей новой механики.

С одной стороны, человек склонен реагировать на необычное, но случайное поведение метрик, и субъективно истолковывать его как нечто содержательное и реальное. С другой стороны, поведение пользователей неоднородно и обусловлено множеством неизвестных факторов, размер влияния которых невозможно оценить и контролировать. Эти факторы вносят случайные флуктуации и шум в данные.

Если в эксперименте принимать решение только по привлекательной наблюдаемой разнице в метриках, то легко выдать желаемое за действительное и спутать результат с воздействием неизвестных факторов. Если поторопиться и принять решение об отсутствии влияния, то существует шанс пропустить практически значимый эффект от экспериментального изменения. Получается, делая вывод только по наблюдаемой разнице в метриках, легко совершить два вида ошибок.

На дистанции такой подход, основанный на эвристических выводах, обернется тем, что в продукт будет добавлено значительное количество фич-пустышек, а также будет пропущена часть действительно полезных механик. Итоговые результаты будут зависеть от выбранной субъективной стратегии принятия решения о наличии или отсутствии эффектов в A/B-тесте.

Поэтому используют модель статистического вывода. Подход хоть и не дает 100% гарантий в принятии правильных решений, но снижает вероятности совершения ошибок и основан уже на формальных математических принципах, а не на субъективной оценке.

Центральное место в этом подходе отведено матрице ошибок.

3.1 Матрица ошибок

Матрица ошибок (confusion matrix) старается устранить разрыв между субъективным восприятием и неизвестной объективной реальностью. Делает это она с помощью вероятностей (не)принять гипотезу, когда она на самом деле (не)верна.

Однако, чтобы с ходу попытаться запомнить эти квадранты и оперировать ими, придется приложить некоторые усилия, поэтому предложу продуктово-ориентированный взгляд и выделю в матрице всего лишь одну сторону.

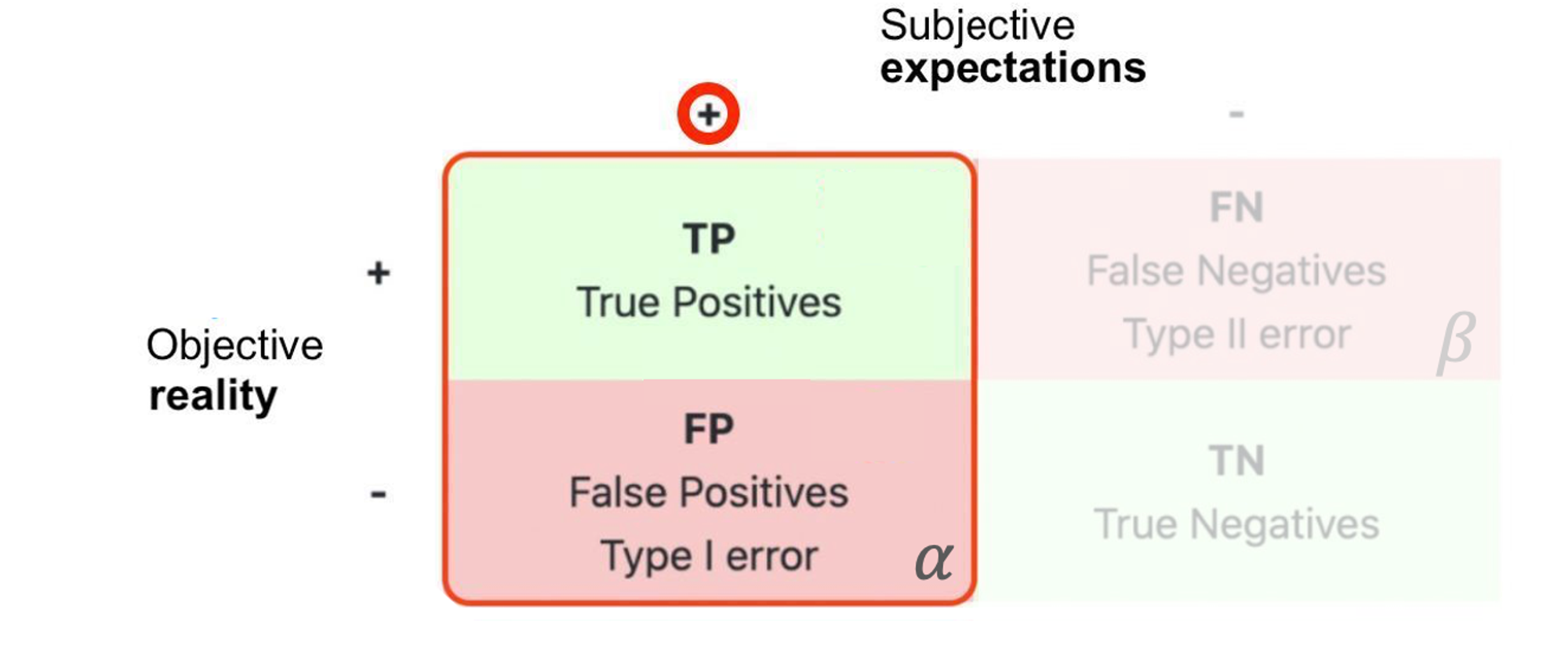
Внимание к одной стороне заключается в простом порядке мыслей.

Реальный эффект от нашей фичи может быть, а может и не быть вовсе, мы все равно этого определенно не узнаем. Продуктовая команда тратит ресурсы и время на разработку фичи и дизайн эксперимента, при этом она априори делает положительные изменения, которые в итоге всегда хочется принимать. Когда эксперимент заканчивается, аналитик остается один на один с двумя стульями:

• Вдруг эффекта от изменения в реальности нет. В таком случае, делая вывод о его наличии, хотелось бы ошибиться как можно в меньшем числе случаев. Это ошибка 1-го рода, ее контролируют с помощью проверки нулевой гипотезы H0 статистическим критерием;

• С другой стороны, когда от нашего изменения эффект действительно есть, хочется, чтобы используемые метрики и статкритерий были достаточно чувствительны к обнаружению этого эффекта. Здесь на помощь приходит расчет MDE/Sample size и Анализ мощности.

Также для запоминая типов ошибок есть хорошая мнемоника:

Когда мальчик прибегал в село и кричал «волки-волки», то сначала сельчане совершили ошибку первого рода, а затем  — второго.

3.2 Нулевая гипотеза

Проверка нулевой гипотезы — это инструмент, контролирующий уровень ошибки 1-го рода. Процент случаев, в которых продуктовая команда готова ошибаться, она определяет сама, ограничив порог принятия фич-пустышек выбранным уровнем значимости alpha.

Нулевая гипотеза — это логический конструкт, воплощающий понятие о том, что на самом деле в эксперименте ничего не произошло, эффекта от нашего изменения нет, а любой эффект, который наблюдается в изменении метрик, обусловлен шумом и случайностью.

Эту идею удобно продемонстрировать на примере t-теста, так как его статистика — наблюдаемый эффект, выраженный разницей средних метрик пользователей в тестовой и контрольной группах.

Под нулевой гипотезой изначально предполагается, что эффекта нет, поскольку две наши группы извлечены из одной генеральной совокупности. При этом у нас есть шанс получить из нее как идентичные выборки, так и полностью непохожие друг на друга.
Если бы мы могли «вытащить» из ГС бесконечно много таких пар выборок, считать разницы средних и построить по ним гистограмму, то они бы распределились нормально. Большая часть значений находилась около нуля, но попадались бы и пары выборок с очень большой разницей средних, как с положительным, так и с отрицательным эффектом.

При дизайне эксперимента выбирается доля краевых, необычных случаев, когда мы готовы ошибиться и принять наблюдаемую разницу за реальный эффект, обычно 5%, — это и есть уровень значимости alpha.

Проведя А/Б-тест, идейно можно «вытащить» из ГС только одну пару выборок, посчитать разницу средних и найти ее место среди остальных в обозначенной модели.

В экспериментах оценивают разные метрики, выраженные в деньгах, процентах, штуках, числе кликов и тд., и, чтобы для их всех иметь универсальное распределение, разницу средних делят на стандартную ошибку (standard error), получая метрику в безразмерной шкале.

Определив место наблюдаемого экспериментального случая в общем распределении, считаем общую долю таких и еще более выраженных случаев, это и будет p-value. Более формально, p-value — это вероятность получить наблюдаемый или более выраженный эффект при условии, что верна нулевая гипотеза.

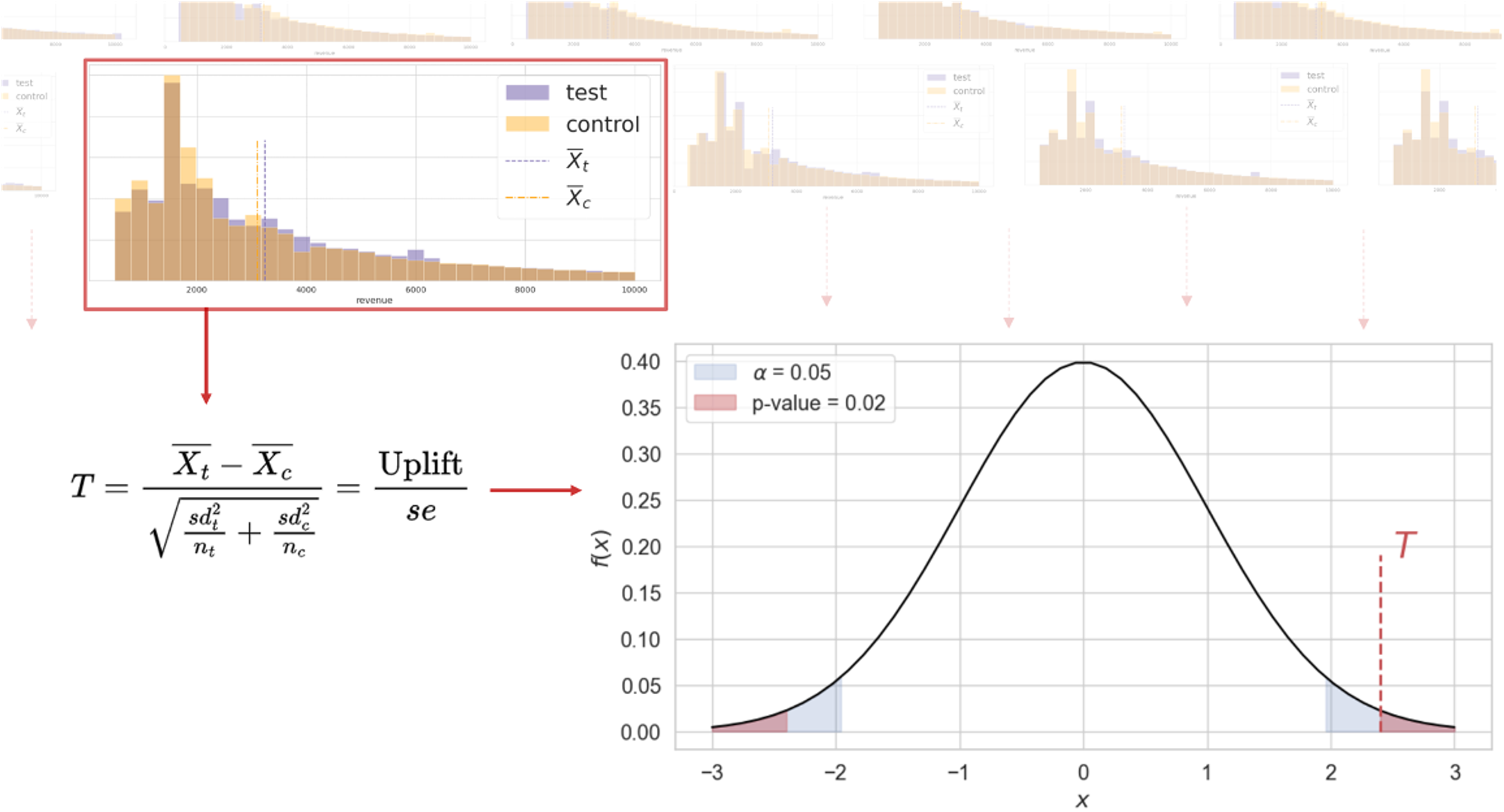
Критерий принятия решения достаточно прост:

• если p-value ≤ alpha, то отклоняем нулевую гипотезу H0, и заявляем, что эффект есть;

• если p-value > alpha, то у нас недостаточно оснований ее отклонить.

На данном этапе возникает большой соблазн интерпретации p-value – чем он меньше, тем больше «уверенность», что Н0 неверна. Но, на самом деле, хоть p-value равен 0.0499, хоть 3.6e-27, вероятность ошибочно отклонить H0 остается на уровне alpha.
Так происходит из-за того, что для нулевой гипотезы p-value распределены равномерно и вероятность случайно получить p-value меньше alpha равняется ее же значению.

3.3 Анализ мощности

Под мощностью подразумевается вероятность корректно отклонить нулевую гипотезу H0 и заявить, что эффект действительно есть.

Мощность зависит от числа наблюдений в имеющихся группах, модели эффекта, получаемого от экспериментального воздействия, и возможности статтеста этот эффект детектировать. В отличие от уровня значимости alpha, которую мы выбираем и фиксируем сами, мощность в конце эксперимента мы не контролируем.

Предварительный дизайн любого эксперимента включает в себя оценку размера выборок, который необходим для того, чтобы задетектить желаемый практический эффект, а в случае ограничения имеющегося трафика можно прикинуть минимальный детектируемый эффект (MDE) при заданных уровнях ошибок 1-го и 2-го родов.

import numpy as np
from scipy import stats

def get_samples_size(sd1, sd2, mde, alpha=0.05, power=0.8):
    quantiles = stats.norm.ppf(q=1-alpha/2) + stats.norm.ppf(q=power)
    var = sd1**2 + sd2**2
    estemated_sample = 2 * var * quantiles**2 / (mde**2)
return estemated_sample

def get_mde(s1, s2, alpha=0.05, power=0.8):
    se = np.sqrt(np.var(s1)/len(s1) + np.var(s2)/len(s2))
    quantiles = stats.norm.ppf(q=1-alpha/2) + stats.norm.ppf(q=power)
return quantiles * se

Обе величины интерпретируются исключительно во время дизайна эксперимента, а после его начала, и особенно в конце, их информативность стремится к нулю, поскольку мы не контролируем каким будет наблюдаемый эффект в эксперименте. Соответсвенно и не знаем какая будет мощность.

На практике иногда встречается, что наблюдаемую разницу сравнивают с MDE, почему не стоит это делать хорошо и подробно рассказано здесь. Чтобы оценить в каких границах может находиться реальный эффект, наблюдаемую разницу задают доверительным интервалом.

Логичнее было бы из формул вывести мощность и определить ее значение для уровня alpha, а вместо MDE подставить наблюдаемую в эксперименте разницу.
Как считать мощность для любой метрики и для любого статкритерия с помощью бутстрапа можно узнать здесь.

import numpy as np
from scipy import stats

def get_power(s1, s2, alpha=0.05):
    mde = abs(np.mean(s1) - np.mean(s2))
    se = np.sqrt(np.var(s1)/len(s1) + np.var(s2)/len(s2))

    one_betta_quantile = mde/se - stats.norm.ppf(q=1-alpha/2)
    power = stats.norm.cdf(one_betta_quantile)
return power

Мощность в конце эксперимента редко может быть информативна когда у вас прокрасилась метрика, т.е. не принципиально мощность получилась 10% или 90%, вероятность что вы примите механику без эффекта останется на уровне alpha. В этом случае, продлевая эксперимент, чтобы набралась мощность, вы просто потратите время и имеющейся трафик.

Об этом можно думать следующим образом — эксперимент проводится не для того, чтобы принимать больше изменений с эффектом, а для того чтобы не принимать много изменений без практического эффекта. По сути вся процедура А/B-тестирования это трейд-офф между длительностью проведения и точностью полученных результатов.

С другой стороны, получив серые результаты в конце эксперимента, если наблюдаемая разница в метриках выглядит привлекательно с бизнесовой точки зрения или если критично остановить эксперимент именно сейчас, то мощность может служить индикатором, что стоит продлить эксперимент и набрать еще наблюдений. Однако, это единичные случаи, которые относятся к важным продуктовым проектам.

Итог

Процедура A/B-тестирования не показывает однозначно истинные эффекты от новых механик, а также не лишена тонкостей и подводных камней в организации и проведении. Вместе с тем, она остается единственным универсальным инструментом, устанавливающим причинно-следственные связи между внесенными изменениями и их влиянием на продукт.

Тем не менее, аккуратный подход к дизайну и понимание сложностей методологии предостерегут от соблазна свободной интерпретации результатов. В том числе, важно помнить, что статистическая значимость и практическая значимость — это разные вещи, и даже если различия статистически значимы, они не всегда имеют практическую ценность для бизнеса.

Итоговый вывод о положительном влиянии экспериментального воздействия делает аналитик на основе согласованности результатов статистического вывода сонаправленных метрик, от продуктовых прокси до бизнесовых денежных, и желательно поста-анализа эксперимента.

Product&data команда СберМаркета ведет соцсети с новостями и анонсами. Если хочешь узнать, что под капотом высоконагруженного e-commerce, следи за нами в Telegram и на YouTube. А также слушай подкаст «Для tech и этих» от наших it-менеджеров.