В первой части рассказа мы познакомились с теорией информации на конкретном примере и сегодня мы продолжим наше исследование. Данный инструмент позволяет описывать мощные идеи, которые имеют множество сфер применения: от сжатия данных до квантовой физики и машинного обучения.
Напомним, что затраты на сообщение длиной L составляют
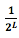 . Мы можем преобразовать выражение и получить длину сообщения стоимостью
. Мы можем преобразовать выражение и получить длину сообщения стоимостью 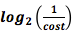 . В итоге, мы тратим p(x) на кодовое слово x длиной
. В итоге, мы тратим p(x) на кодовое слово x длиной 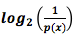 .
.Это лучшая длина сообщения.
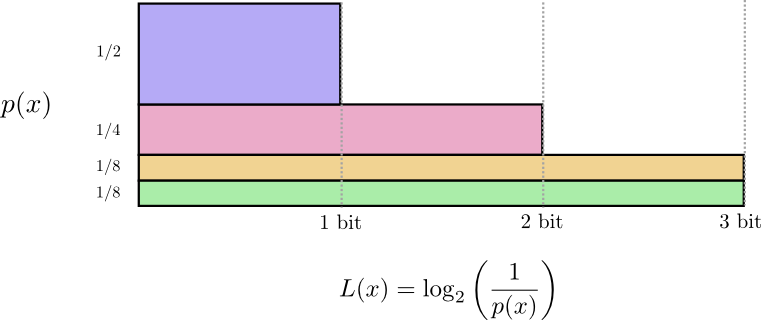
Ранее мы говорили о существовании фундаментального ограничения при создании кратчайшего сообщения на основании распределения вероятностей p. Это ограничение (средняя длина сообщения при использовании наилучшего кода) называется энтропией p и обозначается H(p). Мы можем рассчитать ее, зная оптимальную длину кодовых слов:
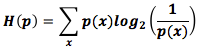
Люди часто описывают энтропию формулой
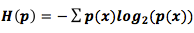 , используя тождество
, используя тождество 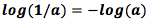 . Я думаю, что первый вариант нагляднее, мы будем и дальше им пользоваться).
. Я думаю, что первый вариант нагляднее, мы будем и дальше им пользоваться).Что бы я ни делал, в среднем я буду передавать количество бит, вычисленное по формуле. Среднее количество информации, необходимое для общения, имеет четкие ограничения по сжатию. Что-нибудь еще? Да! Оно описывает степень неопределенности и дает возможность определить количество информации.
Если бы я знал наверняка, что произойдет, я бы вообще не отправлял сообщение. Если есть два события, которые могут произойти с вероятностью 50%, то мне нужно передать всего 1 бит. Если есть 64 разных события, которые могут произойти с равной вероятностью, то я должен передать 6 бит. Чем точнее совпадают вероятности возникновения событий, тем короче будет средняя длина передаваемых сообщений. Если вероятность сильно «распыляется», то средняя длина сообщений возрастает. Чем неопределенней исход, тем больше информации я могу получить.
Перекрёстная энтропия
Незадолго до своего переезда в Австралию Боб женился на Алисе (другом плоде моего воображения). К моему (и других персонажей в моей голове) удивлению, Алиса не любила собак. Ей нравились кошки. Однако эти двое нашли общий язык, несмотря на их ограниченный словарный запас.
Они говорят одни и те же слова, только с разной частотой. Боб все время говорит о собаках, а Алиса – о кошках.
Сначала Алиса отправляла мне сообщения, используя код Боба. К сожалению, её сообщения были больше, чем могли бы быть. Код Боба оптимизирован для его распределения вероятностей – Алиса же имеет другое распределение вероятностей. Средняя длина сообщения Боба, когда он использует свой код, равна 1,75 бит, но когда его код использует Алиса, то средняя длина сообщения возрастает до 2,25 бита. Было бы хуже, если бы их вероятности распределения еще меньше походили друг на друга.
Средняя длина сообщения, необходимая для определения события из одного распределения вероятностей, если заданная схема кодирования базируется на другом распределении, называется перекрестной энтропией. Перекрестную энтропию рассчитывают по формуле [4]:
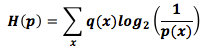
Перекрестная энтропия в этом случае есть соотношение частоты используемых слов любительницы кошек Алисы к частоте используемых слов любителя собак Боба.

Чтобы сохранить стоимость нашего общения низкой, я попросил Алису использовать свой код. К моему облегчению, это снизило среднюю длину ее сообщений. Но возникла новая проблема: иногда Боб случайно использовал код Алисы. Удивительно, но когда Боб использует код Алисы, результат выходит хуже, чем когда Алиса использует его код.
Получаем четыре возможных случая:
- Боб использует свой собственный код H(p) = 1,75 бит;
- Алиса использует код Боба = 2,25 бит;
- Алиса использует свой собственный код H(q) = 1,75 бит;
- Боб использует код Алисы = 2,375 бит.
Здесь все не так очевидно. Например, мы видим, что
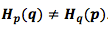 . Есть ли способ как-нибудь рассмотреть, как эти четыре значения соотносятся друг с другом?
. Есть ли способ как-нибудь рассмотреть, как эти четыре значения соотносятся друг с другом?На изображении ниже приведены четыре диаграммы, каждая из которых изображает один из 4 возможных случаев. На каждой диаграмме отображена средняя длина сообщения. Сообщения из одного распределения находятся в одном ряду, а сообщения, использующие один и тот же код – в одном столбце. Это позволяет вам визуально оценить распределения и коды.
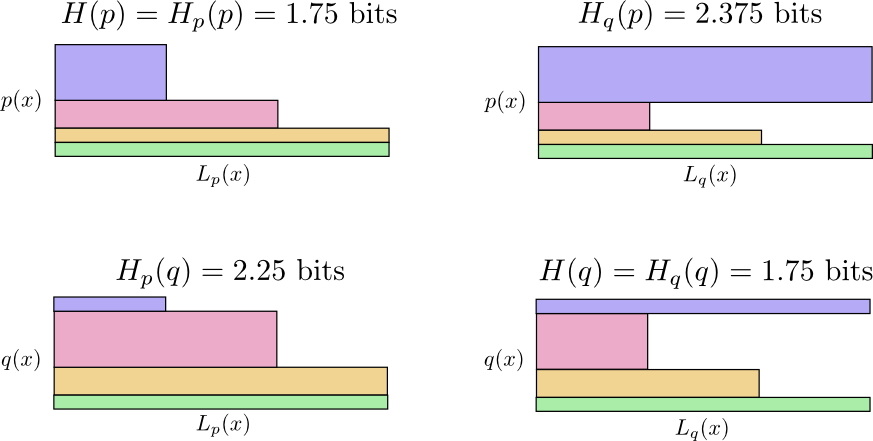
Почему
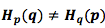 ?
? 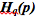 получилось большим, потому что это событие (синее) часто происходит в условиях распределения вероятностей р, но длина кода увеличилась, потому что оно редко происходит в условиях распределения вероятностей q. С другой стороны, частые события из q редко возникают в р, но разница не радикальная, поэтому
получилось большим, потому что это событие (синее) часто происходит в условиях распределения вероятностей р, но длина кода увеличилась, потому что оно редко происходит в условиях распределения вероятностей q. С другой стороны, частые события из q редко возникают в р, но разница не радикальная, поэтому 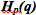 меньше.
меньше.Перекрестная энтропия не симметрична.
Итак, почему необходимо учитывать перекрестную энтропию? Перекрестная энтропия отображает разницу двух распределений вероятностей. Чем сильнее отличаются распределения p и q, тем перекрестная энтропия p по q будет больше энтропии p.
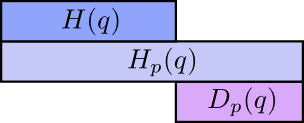
Аналогично, чем сильнее отличается p от q, тем перекрестная энтропия q по p, будет больше энтропии q.
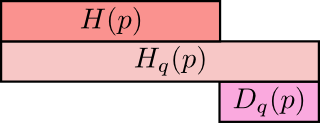
Разница между энтропией и перекрестной энтропией – довольно любопытная вещь: она показывает, насколько увеличиваются сообщения из-за использования кода, оптимизированного для другого распределения. Если распределения совпадают, то разница будет равна нулю. Если разница увеличивается, то увеличивается длина сообщений.
Эта разница называется дивергенцией Кульбака-Лейблера. Дивергенция Кульбака-Лейблера p относительно q обозначается как
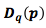 [5] и определяется по формуле [6]:
[5] и определяется по формуле [6]: 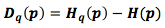
Дивергенция Кульбака-Лейблера – это расстояние между двумя распределениями. Она показывает, насколько они отличаются (если хотите всерьез заняться этим вопросом, то придется разбираться с информационной геометрией).
Перекрестная энтропия и дивергенция Кульбака-Лейблера невероятно полезны в машинном обучении. Нам часто нужно, чтобы одно распределение было похоже на другое. Дивергенция Кульбака-Лейблера позволяет предсказать его с достаточно большой точностью и поэтому часто используется.
Энтропия нескольких переменных
Давайте вернемся к нашему первому примеру про погоду и одежду:
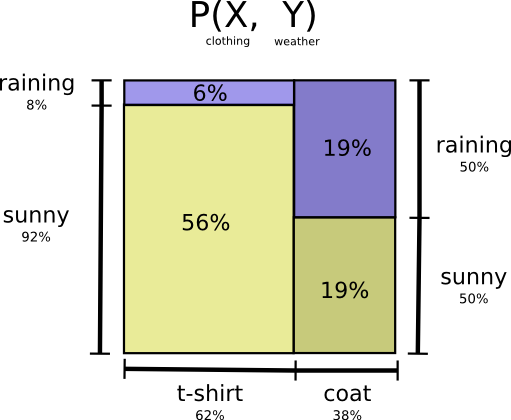
Как и многие родители, моя мама иногда беспокоится, что я оделся не по погоде (у нее есть все основания так думать, потому что я редко ношу пальто зимой). Поэтому она интересуется, какая сейчас погода на улице, и какая одежда на мне надета. Сколько битов я должен отправить ей, чтобы сообщить это?
Самый простой способ – это свести распределение вероятностей:
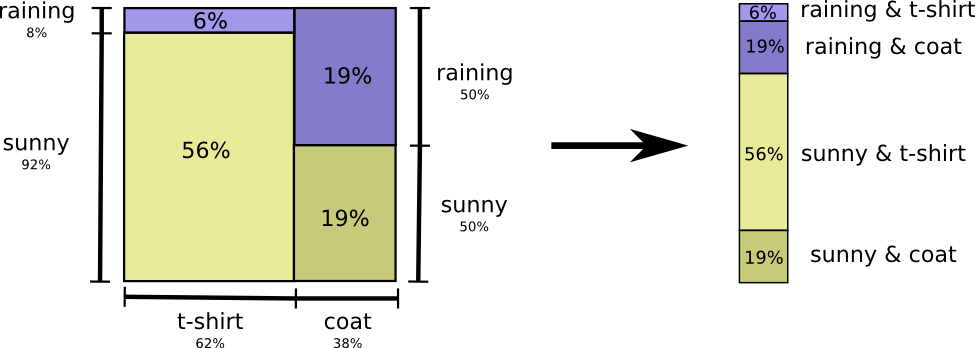
Теперь мы можем определить оптимальные кодовые слова для событий, происходящих с заданными вероятностями, и вычислить среднюю длину сообщения:
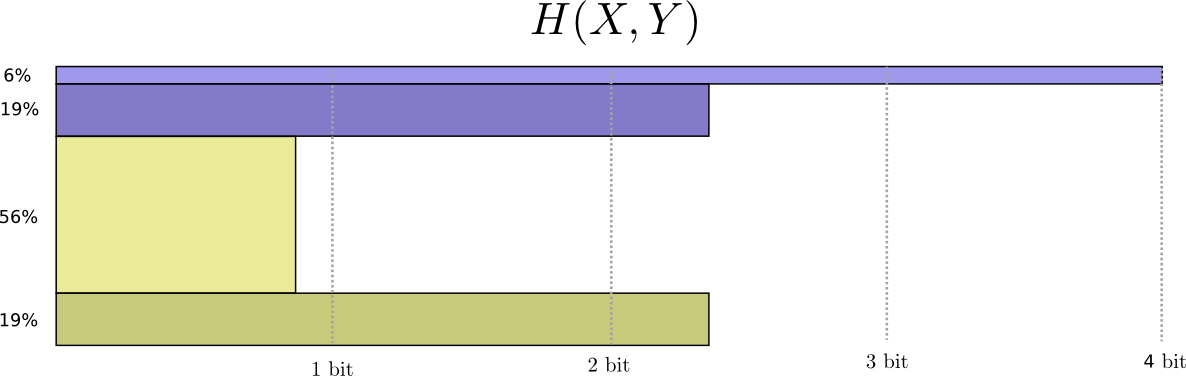
Это называется взаимной энтропией X и Y, которая рассчитывается по формуле:
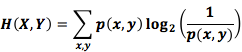
Эта формула похожа на формулу энтропии, только здесь две переменные вместо одной. Однако лучше избежать сведения распределений и ввести третью ось – длину кода. Энтропия в объеме!
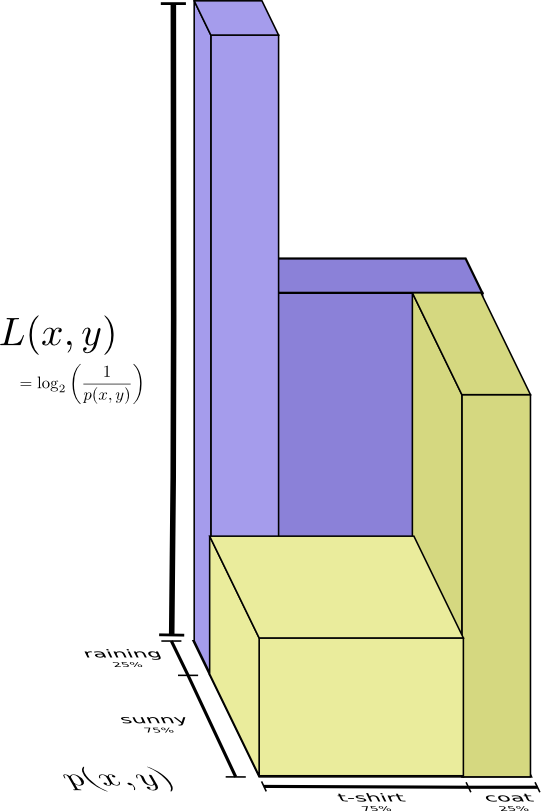
Но предположим, что моя мама уже знает, какая сегодня погода – она посмотрела прогноз. Какое количество информации мне необходимо передать теперь?
Кажется, что мне придется передать такое количество информации, которое позволит сообщить о том, какую одежду я ношу, но на самом деле нужно передать немного меньше, так как погода влияет на то, что я надену. Рассмотрим два случая: когда погода дождливая и когда солнечная.
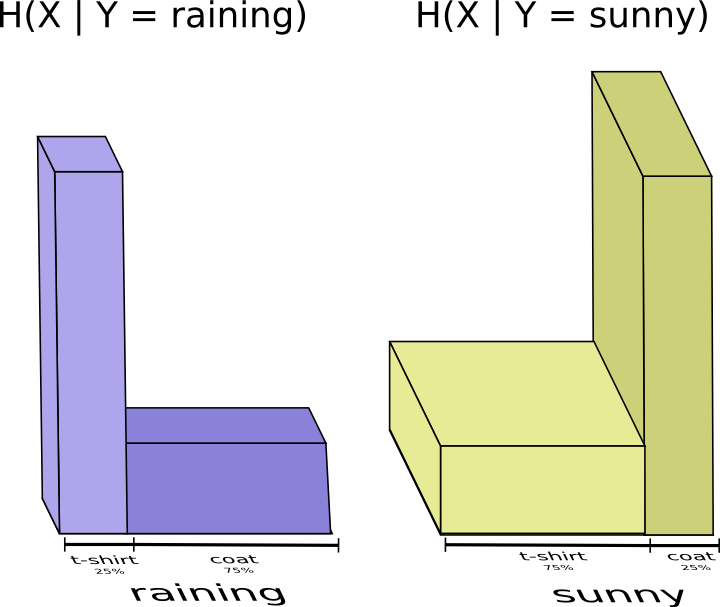
В обоих случаях мне не нужно передавать большое количество информации, потому что погода предполагает правильный ответ. Я могу использовать один код для солнечной погоды, а другой для дождливой. И тут, и там я посылаю меньше информации, чем если бы я использовал общий код для обоих событий.
Чтобы посчитать среднее количество информации, которое мне нужно передать моей маме, я объединю оба случая на одном графике:
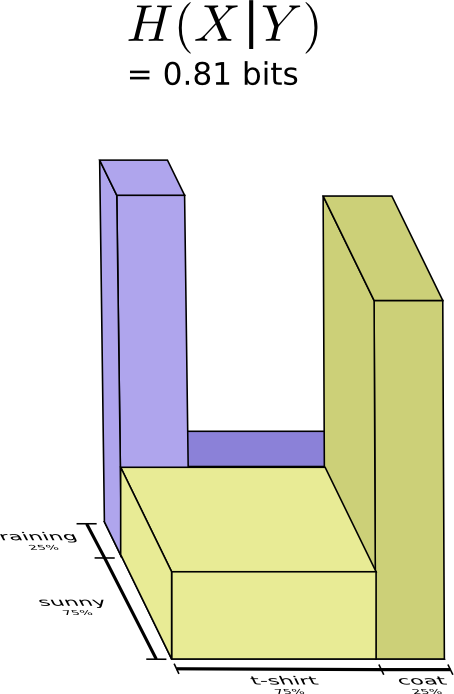
Мы называем это условной энтропией. Условная энтропия вычисляется по формуле:
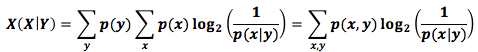
В предыдущем разделе мы выяснили, что если получатель знает, чему равна одна из переменных, то можно передавать меньшее количество информации о второй переменной.
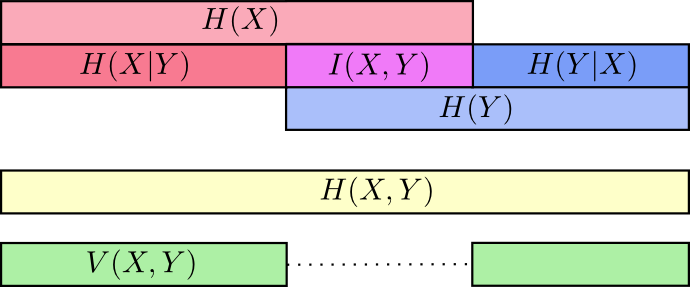
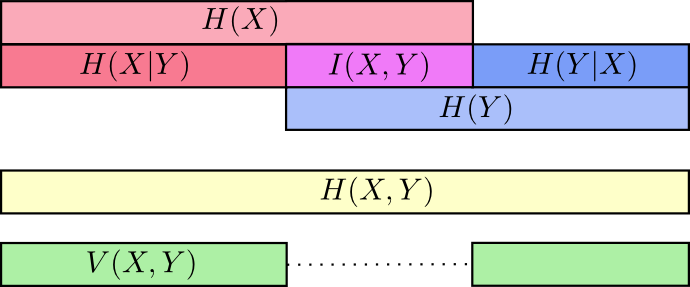
Можно представить объемы инфомрации как полоски. Если у двух полосок имеется общая информация, то они накладываются друг на друга. Например, X и Y содержат общую информацию, поэтому строки Н(Х) и Н(Y) накладываются. Н(X,Y) содежит информацию обоих строк, потому объединяет в себе H(X) и H(Y) [7].
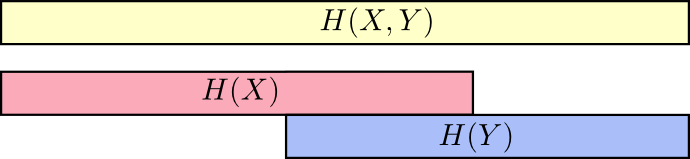
Взглянув на ситуацию под таким углом, становится легче понять множество вещей.
Мы уже отметили, что для передачи X и Y одновременно требуется больше информации (взаимная энтропия Н(X,Y)), чем для передачи X (предельная энтропия Н(Х)). Однако если вы уже знаете Y, то количество передаваемой информации о X (условная энтропия Н(X|Y)) снижается.
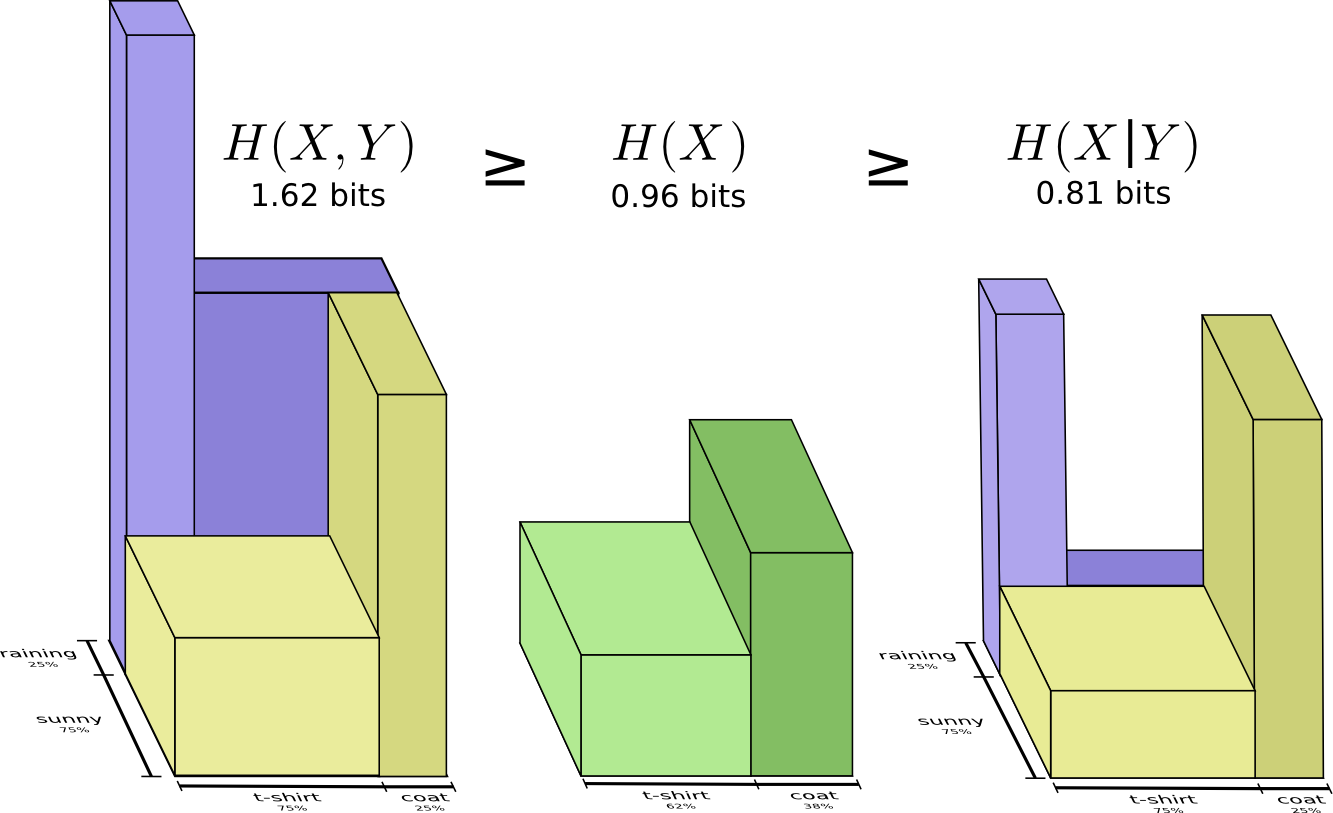
Звучит непонятно, но если снова прибегнуть к помощи полосок, то все становится проще. Н(Х|Y) – это информация, которую мы должны передать, чтобы сообщить X тому, кто уже знает Y (информацию, которая есть в X, но которой нет в Y). Это означает, что H(X|Y) является частью полоски Н(Х), которая не накладывается на H(Y).
Неравенство
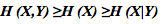 представлено на следующей диаграмме.
представлено на следующей диаграмме.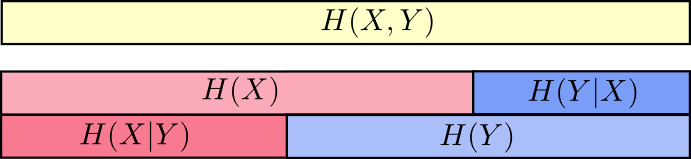
Другое тождество – это Н (X,Y) = H (Y) + Н (Х|Y), где информация в X и Y является суммой информации в Y и информации в X, которой нет в Y.
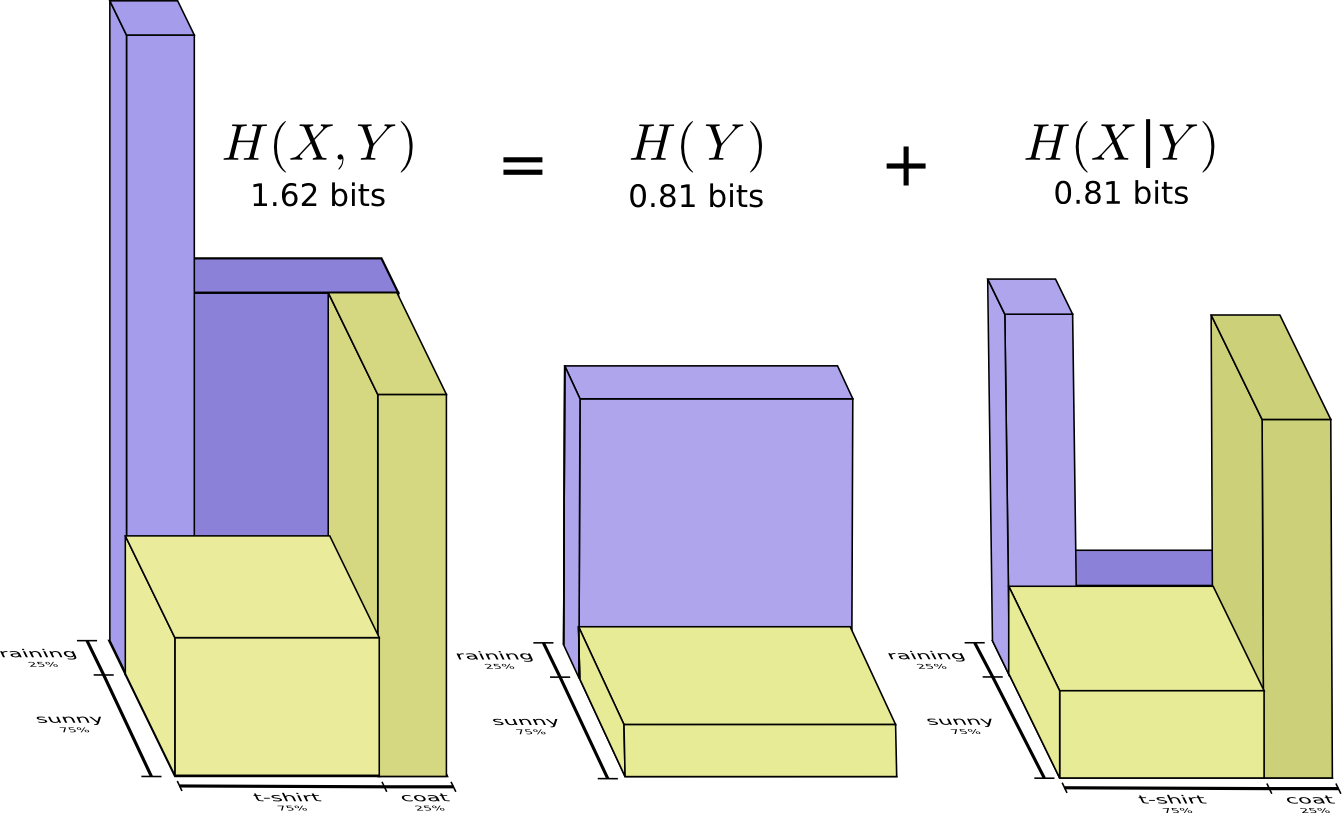
Опять же, уравнение может показаться трудным, но благодаря «полоскам информации» все становится понятнее.
Мы уже разбивали информацию в X и Y несколькими способами. У нас есть информация по каждой переменной Н(Х) и Н(Y). У нас есть сумма информаций обоих событий – Н (X,Y). У нас есть информация, которую несет в себе одно событие, но не несет другое – Н(Х|Y) и Н(Y|X). Кажется, что все связано с понятием общей информации, информации, которую эти два события разделяют. Она называется взаимной информацией I(X,Y) и рассчитывается по формуле [8]:
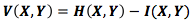
Это уравнение справедливо, потому что сумма Н(Х) + Н(Y) несет в себе две копии взаимной информации, находящейся в X и Y, в то время как в H(X,Y) – только одну (взгляните на предыдущую диаграмму с полосками).
Вариация информации тесно связана с взаимной информацией. Вариация информации – это информация, которая не распределяется между переменными. Мы можем определить ее так:
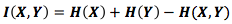
Вариация информации интересна, потому что она дает нам метрику – знание о расстоянии между различными переменными. Вариация информации между двумя переменными равна нулю, если, узнав значение одной, вы можете определить значение другой. Чем независимее переменные – тем большее значение принимает вариация информации.
Как связаны вариация информации и дивергенция Кульбака-Лейблера, которая также дает нам представление о расстоянии? Дивергенция Кульбака-Лейблера является мерой удаленности двух вероятностных распределений от одной переменной или набора переменных. В противоположность этому, вариация информации является мерой удалённости двух переменных в пределах одного распределения. Дивергенция Кульбака-Лейблера определяет расстояние между распределениями, а вариация информации – внутри распределения.
Можно изобразить отношение различных видов информации на одной диаграмме:
Дробные биты
Еще одна трудно понимаемая вещь в теории информации – это дробные биты. Это довольно странно. Что значит половина бита?
Вот простой ответ: часто нам нужна именно средняя длина сообщения. Если в 50% случаев передается один бит, а в другую половину случаев – два бита, то средняя длина сообщения равна полутора битам. Нет ничего странного в том, что средняя длина будет дробной.
Подобный ответ – уклонение от вопроса. Часто оптимальная длина кодовых слов дробная. Что это значит?
Давайте рассмотрим распределение вероятностей. Событие а имеет вероятность равную 71%, а событие b – 29%.
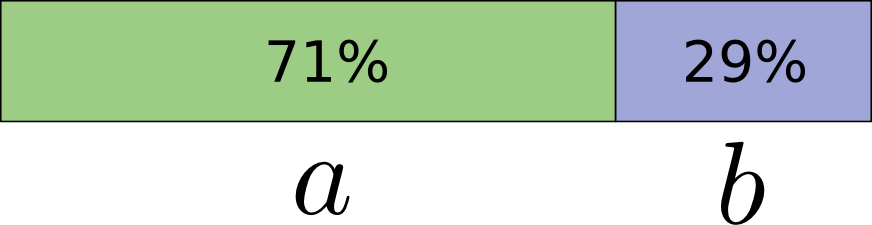
В оптимальном коде 0,5 бита будет использоваться для представления a, а 1,7 бита – для представления b. Если мы хотим отправить одно кодовое слово, то это просто невозможно. Мы вынуждены округлять до целого числа и отправить в среднем в 1 бит.
Но мы сможем усовершенствовать код, если отправим несколько сообщений одновременно. Рассмотрим два события с этим распределением. Если мы отправляем их по отдельности, то должны будем передать два бита. Можем ли мы это улучшить?
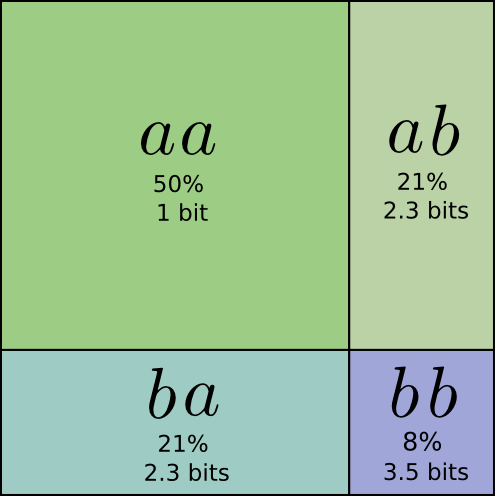
В 50% случаев мы передаем аа, в 21% мы передаем ab или ba и в 8% случаев мы передаем bb. Видим, что идеальный код содержит дробные биты.
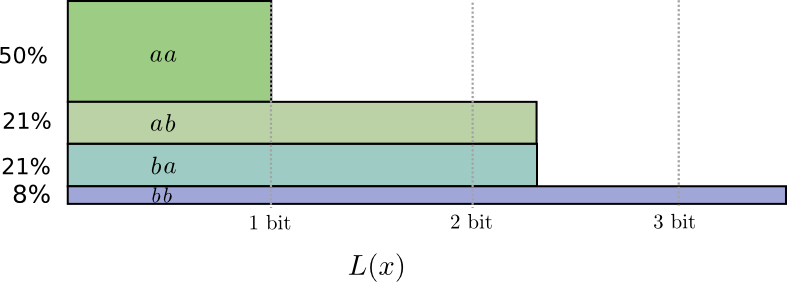
Если мы округлим длины кодового слова, то получим:
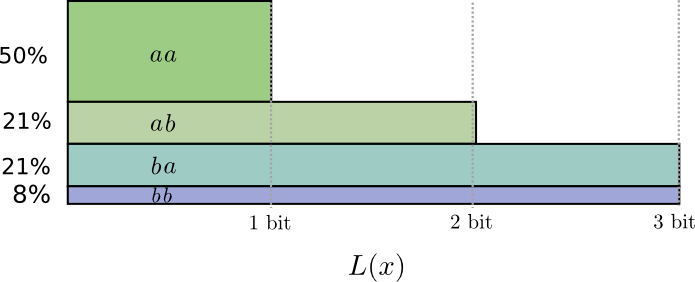
Эти коды дают нам среднюю длину сообщения 1,8 бит. Это меньше, чем когда мы отправляли их независимо. Считайте, что мы передаем 0,9 бит для каждого события. Даже если мы увеличим количество отправлений, то средняя длина сообщения все равно уменьшится. Поскольку n стремится к бесконечности, расходы на округление нашего кода исчезнут, а число битов кодового слова будет стремиться к энтропии.
Кроме того, обратите внимание, что идеальная длина кодового слова была равна 0,5 бит, а идеальная длина кодового слова aa –1 бит. Длина кодового слова увеличивается, даже если она дробная. Таким образом, если мы передаем множество событий одновременно, их длины сложатся.
Мы видим, что использование дробных битов не лишено смысла.
На практике люди используют особые схемы кодирования, которые в разной степени эффективны. Код Хаффмана – основной вид кода, которой мы здесь описали, не может работать с дробными битами (придется группировать символы, как мы делали это выше, или использовать более сложные приемы, чтобы приблизиться к пределу энтропии). Арифметическое кодирование несколько отличается, но может передать дробные биты асимптотически оптимальным способом.
Вывод
Описанные в статье идеи широко применяются при передаче сжатой информации. В теории информации рассматриваются основные приемы сжатия данных, которые дают нам понимание и принципы работы описанных алгоритмов. Но есть ли у всего этого другие применения?
Идеи из теории информации проявляются во многих областях: в машинном обучении, квантовой физике, генетике, термодинамике и даже в азартных играх. Как правило, специалисты-практики в этих областях не интересуются теорией информации, но интересуются её сжатием – это нужно им по специальности. Квантовую запутанность можно описать с помощью энтропии [9]. Многие результаты в статистической механике и термодинамике могут быть получены методом максимальной энтропии [10]. Победы и поражения в азартных играх непосредственно связаны с дивергенцией Кульбака-Лейблера (в определенных случаях) [11].
Теория информации проявляется во всех этих сферах, потому что она предлагает конкретное, формальное описание многих вещей, которые нам нужно выразить. Она дает нам способы измерить неопределенность и различия двух наборов убеждений, а также понять, как связаны между собой два вопроса: как распределяется вероятность, каково расстояние между распределениями вероятностей и насколько зависимы две переменные. Существуют ли альтернативы? Конечно. Но идеи из теории информации понятны, они обладают хорошими свойствами и принципиальным происхождением. В некоторых случаях это именно то, что вам нужно, а иногда – это просто удобно.
Лучше всего я разбираюсь в машинном обучении, давайте немного поговорим о нем. Очень распространенный вид задачи в области машинного обучения – это классификация. Например, мы хотим, посмотрев на изображение, определить: это кошка или собака. Наша модель может сказать что-то вроде: «Вероятность того, что это изображение собаки составляет 80%, а вероятность того, что это изображение кошки – 20%». Давайте предположим, что правильный ответ – собака. Хорошо это или плохо, что вероятность того, что это собака лишь 80%? Было бы лучше, если бы она была 85%?
Это важный вопрос, потому что мы должны иметь представление о том, насколько хороша наша модель, для того, чтобы оптимизировать ее. Что мы должны оптимизировать? Правильный ответ на самом деле зависит от того, для чего нам нужна эта модель: нам интересен только правильный ответ или же нас интересует уверенность в правильности этого ответа? Что, если он неправильный? На эти вопросы существуют множество ответов, и очень часто узнать их невозможно, потому что мы не знаем, как будет использоваться модель, чтобы точно её формализовать. В результате возникают ситуации, когда нам приходится учитывать перекрёстную энтропию [12].
Информация создает новые границы для размышлений о мире. Иногда она помогает нам решить проблему, а иногда просто оказывается невероятно полезной. В этой статье я только слегка затронул теорию информации. Мы не обсуждали такие темы, как корректирующие коды, но я надеюсь, что мне удалось заинтересовать вас этим замечательным разделом математики. Его не стоит бояться.
Примечания
4. Обратите внимание, что это нестандартное обозначение перекрестной энтропии. Общепринятое обозначение – это H(p,q). Оно ужасно по двум причинам. Во-первых, точно такое же обозначение используется для взаимной энтропии. Во-вторых, кажется, что перекрестная энтропия симметрична. Это смешно, поэтому я буду писать 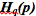 .
.
5. Также нестандартное обозначение.
6. Если расписать понятие дивергенции Кульбака-Лейблера, вы получите:
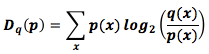
Выглядит немного странно. Как мы должны это понимать?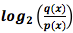 – это просто разница между количеством битов кода, оптимизированных для p и q по x. В целом, выражение показывает ожидаемую разницу между тем, сколько бит понадобится каждому коду.
– это просто разница между количеством битов кода, оптимизированных для p и q по x. В целом, выражение показывает ожидаемую разницу между тем, сколько бит понадобится каждому коду.
7. Идея такой интерпретации была позаимствована из работы Реймонда Йонга (Raymond W. Yeung) «A New Outlook on Shannon’s Information Measures».
8. Если вы распишите определение взаимной информации, то получите:
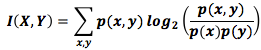
Выглядит в точности как дивергенция Кульбака-Лейблера! Что происходит? Это и есть дивергенция Кульбака-Лейблера P(X,Y) и её аппроксимация Р(Х)P(Y). Другими словами, это количество сэкономленных битов, представляющих X и Y, если они коррелированы.
Визуализация соотношения между распределением и его аппроксимацией в картинках:
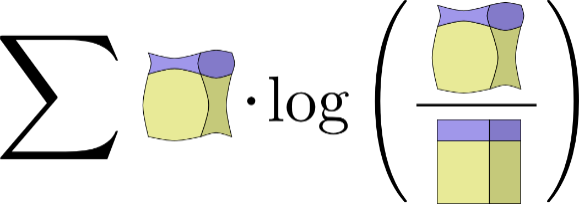
9. Это целая область из квантовой теории информации. Я в ней мало что смыслю, но готов поспорить с чрезвычайно высокой степенью уверенности (поскольку другие работы Майкла были великолепны), что Quantum Computation and Quantum Information («Квантовые вычисления и квантовая информация») Майкла Нильсена и Исаака Чанга (Issac Cuang) – это отличный источник, чтобы начать с ней знакомство.
10. Как человек, который ничего не понимает в статистической физике, я очень нервничаю, когда пытаюсь изложить ее связь с теорией информации.
После того как Шеннон создал теорию информации, многие заметили подозрительные сходства между уравнениями термодинамики и уравнениями теории информации. Э.T. Джейнс (E.T. Jaynes) нашел очень глубокую и принципиальную связь. Предположим, у вас есть система, где вы проводите некоторые измерения давления и температуры. Какой будет вероятность определенного состояния системы? Джейнс предложил, что мы должны принять то распределение вероятности, при котором, с учетом ограничений наших измерений, энтропия максимальна.
(Отмечу, что «принцип максимума энтропии» применим не только в физике). То есть мы должны выбрать вероятность с максимальным количеством неопределенности. Так можно получить множество результатов.
(Прочитайте первые несколько разделов статей Джейнса (часть 1, часть 2). Я был впечатлен тем, каким языком это написано – просто и доступно).
Если вам интересно, но не хочется разбираться в оригинальных работах, в работе Ковера и Томаса (Cover & Thomas) есть раздел, где они выводят статистическую версию второго закона термодинамики из цепей Маркова.
11. Связь между теорией информации и азартными играми была впервые описана Джоном Келли (John Kelly) в своей работе «Новая интерпретация скорости передачи информации» (A New Interpretation of Information Rate). Она написана удивительно доступным языком, хотя и требует понимания нескольких понятий, которые я не разобрал в своей статье.
Келли заметил, что энтропия используется во многих функциях стоимости, которые не имели никакого отношения к кодированию информации, и хотел найти конкретную причину этого. При написании статьи меня беспокоила эта же проблема, поэтому я по достоинству оценил работу Келли. Тем не менее, я не считаю, что Келли был достаточно убедителен: он пришел к энтропии только потому, что реинвестировал всю прибыль на каждом новом этапе. Любые другие схемы не ведут к энтропии.
Связь, которую провел Келли между ставками и теорией информации можно найти в книге «Elements of Information Theory» (Элементы теории информации) Ковера и Томаса.
12. Это не решит проблему, но я не могу не защищать дивергенцию Кульбака-Лейблера.
Существует постулат, который Ковер и Томас называют леммой Стейна, хотя он не имеет прямого отношения к самой лемме. Если не углубляться, то вот что там говориться.
Предположим, у вас есть данные одного из двух распределений вероятностей. Как определить, откуда они поступили? Чем больше данных вы получите, тем выше будет ваша уверенность. Например, в среднем ваша уверенность может вырасти в 1,5 раза за каждый из результатов полученных данных.
Насколько сильно вырастет ваша уверенность, зависит от различия распределений. Если различия велики, то определение нужного распределения не займет много времени. Но если их отличия незначительны, то вам придется просмотреть очень много данных.
В общих чертах, в лемме Стейна говорится, что темп роста уверенности контролируется дивергенцией Кульбака-Лейблера (здесь есть тонкость с ложноположительными и ложноотрицательными результатами). Кажется, что это хороший повод изучить дивергенцию Кульбака-Лейблера.
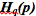 .
.5. Также нестандартное обозначение.
6. Если расписать понятие дивергенции Кульбака-Лейблера, вы получите:
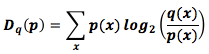
Выглядит немного странно. Как мы должны это понимать?
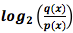 – это просто разница между количеством битов кода, оптимизированных для p и q по x. В целом, выражение показывает ожидаемую разницу между тем, сколько бит понадобится каждому коду.
– это просто разница между количеством битов кода, оптимизированных для p и q по x. В целом, выражение показывает ожидаемую разницу между тем, сколько бит понадобится каждому коду.7. Идея такой интерпретации была позаимствована из работы Реймонда Йонга (Raymond W. Yeung) «A New Outlook on Shannon’s Information Measures».
8. Если вы распишите определение взаимной информации, то получите:
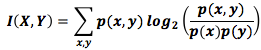
Выглядит в точности как дивергенция Кульбака-Лейблера! Что происходит? Это и есть дивергенция Кульбака-Лейблера P(X,Y) и её аппроксимация Р(Х)P(Y). Другими словами, это количество сэкономленных битов, представляющих X и Y, если они коррелированы.
Визуализация соотношения между распределением и его аппроксимацией в картинках:

9. Это целая область из квантовой теории информации. Я в ней мало что смыслю, но готов поспорить с чрезвычайно высокой степенью уверенности (поскольку другие работы Майкла были великолепны), что Quantum Computation and Quantum Information («Квантовые вычисления и квантовая информация») Майкла Нильсена и Исаака Чанга (Issac Cuang) – это отличный источник, чтобы начать с ней знакомство.
10. Как человек, который ничего не понимает в статистической физике, я очень нервничаю, когда пытаюсь изложить ее связь с теорией информации.
После того как Шеннон создал теорию информации, многие заметили подозрительные сходства между уравнениями термодинамики и уравнениями теории информации. Э.T. Джейнс (E.T. Jaynes) нашел очень глубокую и принципиальную связь. Предположим, у вас есть система, где вы проводите некоторые измерения давления и температуры. Какой будет вероятность определенного состояния системы? Джейнс предложил, что мы должны принять то распределение вероятности, при котором, с учетом ограничений наших измерений, энтропия максимальна.
(Отмечу, что «принцип максимума энтропии» применим не только в физике). То есть мы должны выбрать вероятность с максимальным количеством неопределенности. Так можно получить множество результатов.
(Прочитайте первые несколько разделов статей Джейнса (часть 1, часть 2). Я был впечатлен тем, каким языком это написано – просто и доступно).
Если вам интересно, но не хочется разбираться в оригинальных работах, в работе Ковера и Томаса (Cover & Thomas) есть раздел, где они выводят статистическую версию второго закона термодинамики из цепей Маркова.
11. Связь между теорией информации и азартными играми была впервые описана Джоном Келли (John Kelly) в своей работе «Новая интерпретация скорости передачи информации» (A New Interpretation of Information Rate). Она написана удивительно доступным языком, хотя и требует понимания нескольких понятий, которые я не разобрал в своей статье.
Келли заметил, что энтропия используется во многих функциях стоимости, которые не имели никакого отношения к кодированию информации, и хотел найти конкретную причину этого. При написании статьи меня беспокоила эта же проблема, поэтому я по достоинству оценил работу Келли. Тем не менее, я не считаю, что Келли был достаточно убедителен: он пришел к энтропии только потому, что реинвестировал всю прибыль на каждом новом этапе. Любые другие схемы не ведут к энтропии.
Связь, которую провел Келли между ставками и теорией информации можно найти в книге «Elements of Information Theory» (Элементы теории информации) Ковера и Томаса.
12. Это не решит проблему, но я не могу не защищать дивергенцию Кульбака-Лейблера.
Существует постулат, который Ковер и Томас называют леммой Стейна, хотя он не имеет прямого отношения к самой лемме. Если не углубляться, то вот что там говориться.
Предположим, у вас есть данные одного из двух распределений вероятностей. Как определить, откуда они поступили? Чем больше данных вы получите, тем выше будет ваша уверенность. Например, в среднем ваша уверенность может вырасти в 1,5 раза за каждый из результатов полученных данных.
Насколько сильно вырастет ваша уверенность, зависит от различия распределений. Если различия велики, то определение нужного распределения не займет много времени. Но если их отличия незначительны, то вам придется просмотреть очень много данных.
В общих чертах, в лемме Стейна говорится, что темп роста уверенности контролируется дивергенцией Кульбака-Лейблера (здесь есть тонкость с ложноположительными и ложноотрицательными результатами). Кажется, что это хороший повод изучить дивергенцию Кульбака-Лейблера.

