Ничто так не скрыто от нас, как то, что лежит на поверхности.
Сунь Цзы и Чжугэ Лян (вольный перевод)

Предисловие

Случилось сие в одном из роликов на YouTube. При просмотре программистского урока нужно было срочно перевести 377 в десятичную систему. Мы не стали раскладывать это на тройки бит, представлять степени восьмёрки или просто не обращать на это внимание и пропустить этот неважный момент. Мы запустили калькулятор в операционной системе, пододвинули его окно к центру экрана и там всё выяснили. Да, это оно — число 255.

Конечно, не нужно рассказывать, что бывает в более сложных случаях. Порой дело доходит до листика в тетради, лежащей рядом с компьютером как раз для таких случаев. У каждого найдётся парабола или что-то около того, пересекающее что-то около того.

Первый контакт

Как и следовало ожидать, при использовании Emacs на протяжении месяцев или просто многих лет наступает Emacs головного мозга. Поэтому такие случаи не проходят даром и среди ночи в голове возникает вопрос: «Как же всё-таки в Emacs'е перевести 377? Он хотя бы это умеет? Ну, хотя бы 8 возведёт в степень?».

Наутро, зарядившись энергией в виде чая с горстью шоколадных конфет, мы открываем Emacs и начинаем его исследование.

Начинаем с операций

Понятно, что введя Alt + x и calc , мы первым делом видим обычный стековый калькулятор, которых писали, наверное, штук сто вот этими вот руками. И как бы не хотелось повторять этот путь в сто первый раз, обнаружив, что он не умеет ничего.

Методом тыка сначала делаем + — * /

5 <RET> 7 <RET> +

5 <RET> 7 <RET> -

5 <RET> 7 <RET> *

5 <RET> 7 <RET> /


Потом

8 <RET> 8 <RET> *


О! А вот и квадрат восьмёрки! А где квадрат, там и куб!

Открываем хелп

Конечно, все знают, что русский человек (сссрский, имперский и др.) не будет начинать с инструкции, а сначала попробует всё сломать, потом починить, а потом уже инструкцию читать в поисках пропущенных секретов.

Не скажу, что в этот раз с инструкции всё началось, так как в отличие от многих я не отключаю меню Emacs'а, а пользуюсь им для вспоминания сочетаний клавиш во всяких редких режимах.

Вот и в этот раз я начал обзор с меню калькулятора



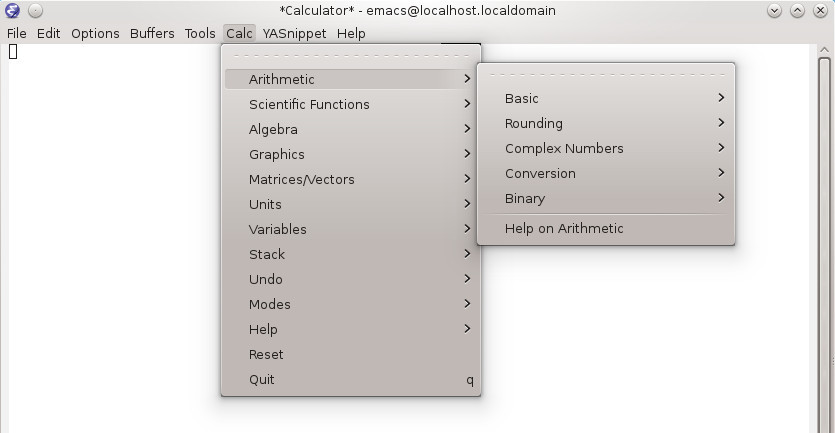
Для того, чтобы открыть хелп, нужно ввести Ctrl + x + * + i . А чтобы открыть туториал, нужно ввести Ctrl + x + * + t .

Их по-разному можно открыть, но, как показала практика, сочетание Ctrl + x + * + <клавиша> используется очень часто и сделано специально для удобного управления калькулятором в процессе другой работы.

Поэтому открыть калькулятор можно через Ctrl + x + * + c , а запустить калькулятор в текущем буфере можно через Ctrl + x + * + e .

Поднимаем планку

Примерно день ушёл на проверку всех опций из меню. Среди них есть такие, как нахождение следующего простого числа, поэтому такое нельзя было просто пропустить, хотелось убедиться, что это действительно работает.

Наибольший общий делитель (НОД) теперь можно не писать, здесь он просто есть. Надо ввести два числа и нажать k g, где k означает комбинаторику, а g — gcd (Greatest Common Divisor).

Факториал 3000 (своеобразная проверка на скорость) вычисляется не без труда, но всё же вычисляется секунд за пятнадцать.

Транспонирование матрицы, нахождение её определителя или скалярное умножение векторов выполняется легко и со свистом.

На минуту я забыл, за чем пришёл, выполняя операции одну за другой, не веря собственным глазам. А за чем же я пришёл?

Продолжаем

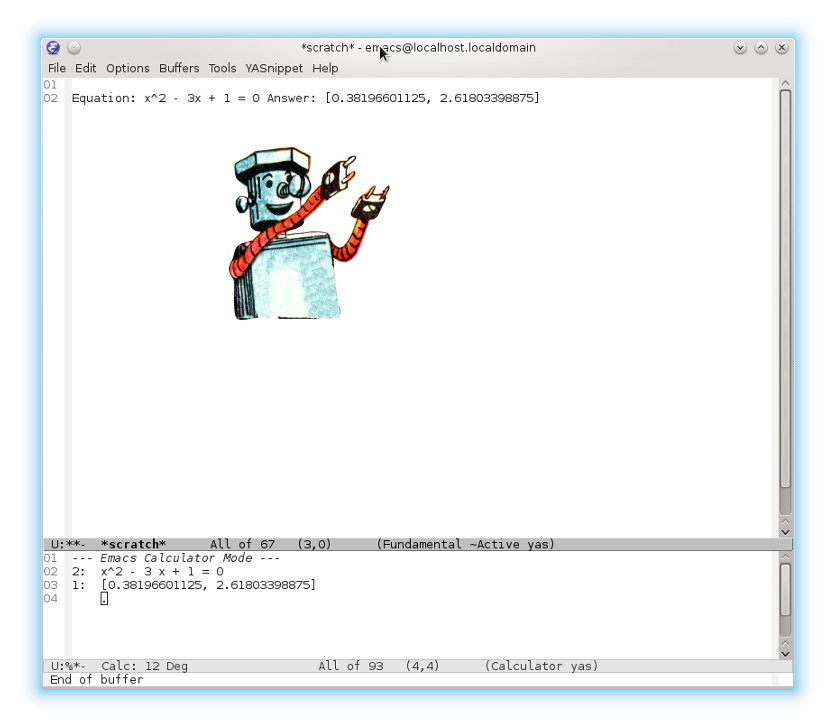
На второй день стало интересно, вычислит ли он систему уравнений методом Крамера. Раз определители есть, то и решение методом Крамера можно найти. Раньше-то я в редакторе это писал много раз, даже навыки уже сложились по вычислению определителей в редакторе.

Но это не потребовалось. Оказалось, что достаточно просто ввести три уравнения, а потом запросить их решение. Да, прямо как в Вольфраме.

Найдём первую попавшуюся систему

 2y +  x +  z = -1
 -z -  y + 3x = -1
-2x + 3z + 2y =  5


Надо просто её выделить Ctrl + x + h , скопировать Alt + w , перейти в калькулятор Ctrl + x + * + * , вставить её Ctrl + y , упаковать уравнения в вектор 3 v p , нажать a P и в ответ на вопрос «По каким переменным искать корни?» ввести x y z .

В стеке появится вектор с ответами, дальше мы просто нажимаем y и вектор с ответами вставляется в позицию курсора в исходном буфере с уравнениями.

[[ 0., -2., 3. ]] 2y +  x +  z = -1
 -z -  y + 3x = -1
-2x + 3z + 2y =  5


Если бы мы курсор оставили в конце системы уравнений, то ответ вставился бы туда.

Пришло время развернуться

Сила стека

При пользовании калькулятором в течение какого-то времени становится неудобно от того, что в стеке начинают накапливаться значения. При этом ты не знаешь, возможно ли их удалить, так как среди них есть нужные, поэтому любой эксперимент может закончится потерей.

Так идут часы, пока в одну прекрасную минуту ты не решаешься всё-таки открыть хелп и потратить время на его чтение. К счастью, все комбинации подобраны максимально удобно, так что там даже присутствует и поддерживается некая симметрия действий.

Вот эти числа с двоеточиями в стеке в начале каждой строки являются как бы адресами. Во многих командах ввод положительного аргумента означает «несколько штук», а ввод отрицательного аргумента означает «такой-то номер».

К примеру, есть у нас число пять в стеке

1: 5


Если мы нажмём <RET> (Enter), то оно скопируется и у нас будет

2: 5
1: 5


Вот эта двойка равна количеству элементов в стеке, она же является адресом первого числа пять, а число 1 является адресом второго числа пять.

У команды <RET> есть аргумент, который по умолчанию равен 1. Когда мы нажимаем <RET> , он копирует столько элементов от вершины стека (вершина — в самом низу). Поэтому, если мы введём Alt + 2 + <RET> , он возьмёт два элемента и скопирует их

4: 5
3: 5
2: 5
1: 5


Если же аргумент отрицательный, то он берёт элемент с таким адресом (если минус убрать). Поэтому, если мы введём теперь Alt + — + 4 + <RET> , он скопирует элемент по адресу 4

5: 5
4: 5
3: 5
2: 5
1: 5


Большинство основных операций работают по той же схеме. Если нужно удалить три элемента, то пишем Alt + 3 + <DEL> , где <DEL> — это backspace. Если же нужно удалить элемент с адресом 3, то пишем Alt + — + 3 + <DEL> .

Если почитать хелп ещё более подробно, то к этим операциям можно найти такие своеобразные операции из антимира, состоящие из чёрной материи. Например, для <RET> существует операция Ctrl + j , для <DEL> существует Alt + <DEL> , а для <TAB> существует Alt + <TAB> .

Смысл этих операций точно такой же, только аргумент меняется по знаку. Поэтому, если ввести Alt + 3 + Ctrl + j , то он не три элемента скопирует, а элемент с адресом 3, а если ввести отрицательный аргумент, то он скопирует не элемент с адресом 3, а три элемента.

Если нужно очистить весь стек, то нужно нажать Alt + 0 + <DEL> .

Есть множество путей

Поначалу кажется, что всё можно делать только одним способом, который надо просто выучить. Но со временем открываются многие способы достижения одного и того же результата.

Например, как можно ввести матрицу?

Самое первое, что приходит на ум, — это написать её в буфере и потом просто скопировать.

Вот это

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]


Превращается вот в это

1: [ [ 1, 2, 3 ]
     [ 4, 5, 6 ]
     [ 7, 8, 9 ] ]


Второе, что приходит на ум, — это использование внутреннего средства.

Матрица — это три вектора

1 <RET> 2 <RET> 3 <RET> 3 v p
4 <RET> 5 <RET> 6 <RET> 3 v p
7 <RET> 8 <RET> 9 <RET> 3 v p
3 v p


Третье, что приходит на ум, — это использование внутреннего и удобного средства.

1 <RET> 2 <RET> 3 <RET> 4 <RET> 5 <RET> 6 <RET> 7 <RET> 8 <RET> 9 <RET>
[3, 3]
v p


И четвертое, что приходит на ум, — «А её нельзя просто ввести?»

[ 1 <SPC> 2 <SPC> 3 ; 4 <SPC> 5 <SPC> 6 ; 7 <SPC> 8 <SPC> 9 ] ]


У команды pack есть симметричная — unpack, поэтому, если нужно разложить матрицу на векторы или вектор разложить на числа, то мы просто нажимаем v u .

Привлекаем внешние средства

По мере ковыряния в калькуляторе вдруг начинаешь обращать внимание на окружающие буферы и постепенно возникает вопрос: «А какие средства обычного Emacs'а можно привлечь при работе в калькуляторе?»

Поначалу мы просто находим n-ую производную многочлена путём записи макроса и повторения его n раз через аргумент макроса.

Например, вводим выражение

' x^5 + 4 x^3 + 2 x + 1 <RET>


Затем нажимаем F3, чтобы начать запись макроса. Потом нажимаем a d, чтобы вычислить производную. Затем на вопрос «По какой переменной?» вводим x . Потом нажимаем F4, чтобы закончить запись макроса.

Делаем отмену вычисления, нажав Ctrl + / или применяя внутреннюю отмену калькулятора — букву U.

Имея первоначальное выражение

1: x^5 + 4 x^3 + 2 x + 1


Нажимаем Alt + 3 + F4 и в результате имеем третью производную

1: 60 x^2 + 24


Если же мы нажмём Ctrl + x + z , а потом z z , то мы постепенно получим ноль.

Уходим во внешний мир

Через какое-то время калькулятор закрывается и мы возвращаемся к нашей обычной работе, к нашим обычным развлечениям.

И вот в один прекрасный момент мы читаем, в Emacs'е естественно, историю про лису, которая прыгала-прыгала через ленивую собаку и прыгнула 1024 раза. Постойте, скажете вы, разве лиса может прыгнуть столько раз прямо точь в точь, если она не компьютерная? Надо это дело исправить.

У нас имеется следующий текст

The quick brown fox has jumped over the lazy dog 1024 times.


Наводим курсор на 1024 и осторожно нажимаем Ctrl + x + * + w . Дальше нажимаем Q, а потом так же осторожно нажимаем Ctrl + x + * + w .

И у нас получается

The quick brown fox has jumped over the lazy dog 32 times.


Вот это уже больше похоже на правду. То есть, чтобы что-то вычислить, калькулятор совсем не обязательно открывать, достаточно лишь понажимать какие-то кнопки.

А вот то самое

Вспомнил, за чем я заходил

Ctrl + x + * + *
8#377 <RET>
d 2
d 8
d 6
d 0
Ctrl + x + * + *


И напоследок

Было время, когда я писал функцию на питоне

2016
1
1
Alt + - + 14 v p
255
+


Прилагаю тут список единиц, которые он может конвертировать, в калькуляторе они находятся по u v .