Цель этого рассказа — поделиться способами решения проблемы, над которой работали авторы при разработке рекомендательного сервиса imhonet.ru. Поскольку проблема не является чисто научно-технической, а скорее находится на стыке технологий и бизнеса и может быть полезна более широкой аудитории, чем обычный технический отчёт, мы выбрали именно такой формат представления нашей работы — попытались написать рассказ настолько простым языком, насколько это возможно. Первая часть рассказа посвящена довольно подробному обоснованию того, как правильно измерять качество работы алгоритмов рекомендательной системы. А в конце иллюстративно перечислено несколько примеров, в которых мы проводили эти измерения для решения конкретных задач.

Проблема метрики для рекомендера

Всякая рекомендательная система помогает решать определённую бизнес-задачу. А результат измеряется понятными для бизнес-задачи способами — количеством поcетителей, продажами, CTR, и т.д. Однако качество рекомендательного алгоритма таким способом измерить слишком сложно — оно будет зависеть от огромного множества условий, среди которых рекомендательный алгоритм сам по себе может оказаться делом десятым.


Так оказывается, что формальные численные критерии к рекомендательным алгоритмам нужно придумывать их разработчикам в отрыве от бизнес-задачи. В результате, работы, посвящённые рекомендательным системам, полны разными полезными численными метриками, но иногда довольно мудреными по отношению к решаемым задачам.

Оптимальный подход, о котором пойдет речь, — это попытаться сконструировать метрику непосредственно под бизнес-задачу. Ясно, что это легче сказать, чем сделать, поэтому дальше речь пойдет о конкретном примере: как это сделано для рекомендательного сервиса кинофильмов imhonet.ru. Хотя мы проверили этот подход именно на фильмах, но он достаточно отвлечен, в чем можно убедиться, заменив слово фильм во всей следующей истории на что-либо еще.

Продукт сервиса и фидбэк пользователей

Продукт сервиса — персональные списки рекомендуемых фильмов. Фидбэк довольно точный, а поэтому ценный — непосредственные оценки этим фильмам:


Имеет смысл использовать такой хороший фидбэк на полную катушку. Оценки, ради удобства в терминологии, мы будем иногда называть «сигналами удовлетворённости».

Почему в задаче речь идёт именно о списке рекомендаций, а, например, не об одном элементе? Потому же, почему поисковик выдает список ссылок: он не знает полного контекста запроса. Если бы знал полный контекст (например, содержание головы пользователя), то, наверное, единственный результат имел бы смысл, а иначе часть работы все равно остается для автора запроса.

Рекомендации и оценки

Сопоставляем фидбэк пользователей — оценки, со списками элементов, которые мы рекомендовали:


Нам потребуется рассмотреть следующие ситуации:

• Hit — фильм рекомендовался, и есть позитивная оценка
• Mishit — фильм рекомендовался, но оценка негативная
• Recommended but not rated — фильм рекомендовался, но оценки нет
• Rated but not recommended — позитивная оценка фильму есть, но он не рекомендовался

Пройдемся по ним последовательно.

Hit

Если фильм человеку рекомендовался, и от него есть позитив?ный сигнал, значит, мы попали точно. Именно такие случаи нас и интересуют, поэтому назовём их успехами и будем максимизировать их количество:

Mishit

Тот фильм, который рекомендовался и получил негативный сигнал это — пример случаев, которых мы должны избегать. Возможно даже, что избегание таких случаев важнее, чем максимизация количества случаев успеха.

Это немного неожиданно, но практика показала, что такими случаями можно просто пренебречь — вероятность совпадения негативных сигналов с элементами из списка рекомендаций, которую дает какая-нибудь вменяемая рекомендательная система, оказывается слишком незначительной, чтобы заметно повлиять на значение метрики. Поэтому, специально рассматривать этот случай оказывается не нужно. А это значит, что к негативным оценкам метрика будет нечувствительна. Точнее, негативная оценка будет эквивалентна просто отсутствию оценки у пользователя (это будет полностью ясно чуть позже).

Recommended but not rated

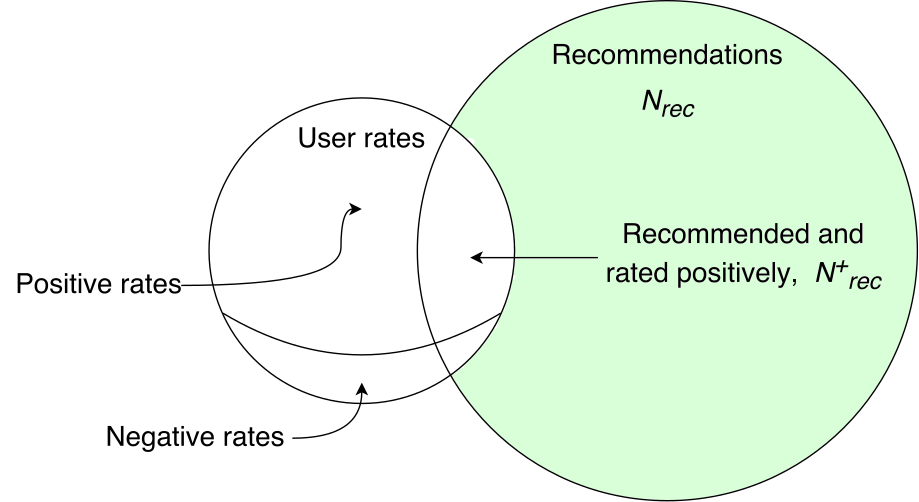
Если фильм рекомендовался, но позитивного сигнала у нас нет, то кажется, что это ничего не значит. Мало ли почему так случилось — человек мог не посмотреть фильм или не оценить его. Однако, с точки зрения всей аудитории, всей массы сигналов, это те случаи, для которых вероятность, что фильм почему-то не заслужил для человека высокой оценки, однозначно выше, чем для случаев явного успеха. Поэтому можно было бы засчитать этот случай тоже негативным, но насколько эта вероятность выше, оценить очень сложно. То есть, установить степень негативности мы не можем. В результате, имеет смысл считать, что просто ничего не произошло и не учитывать случай явно. На практике оказывается, что таких случаев большинство — во-первых, мы всегда должны посоветовать некоторый избыток (т.е. взять значение N_rec с запасом), во-вторых, большинство людей, как правило, не отмечает оценкой каждый просмотренный фильм (т.е., мы видим лишь часть их оценок).

Rated but not recommended
Противоположный случай — фильм не рекомендовался, а позитивный сигнал есть, то есть, рекомендер упустил возможность увеличить количество успехов. Пока такие возможности встречаются, можно улучшать результат:


Если рекомендации содержат все позитивные сигналы, точность системы максимальная — улучшать больше нечего:


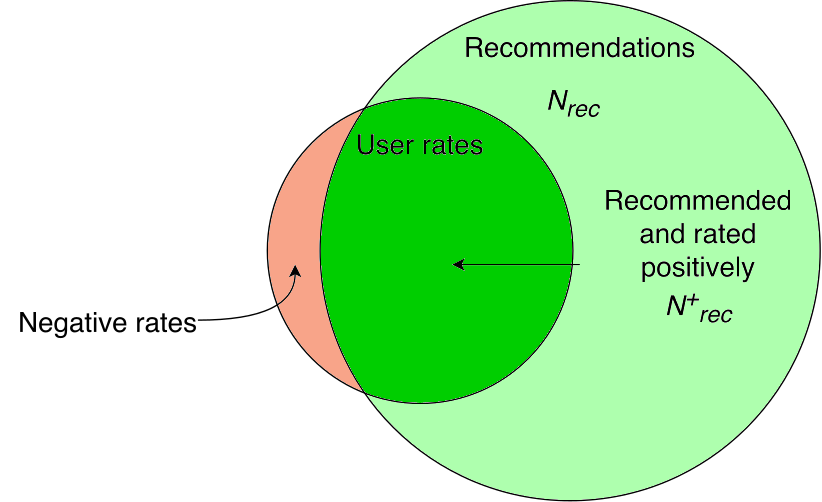
Итак, в нашей схеме получается, что улучшение качества рекомендаций — это увеличение количества успехов в списке рекомендаций (размер которого, N_rec фиксирован).

Метрика precision

Если вместо просто количества успехов мы будем использовать значение precision (p), т.е. разделим — количество успехов на N_rec, то, по существу, ничего не изменится: вместо количества успехов будем максимизировать величину, которая отличается от него лишь делением на константу:


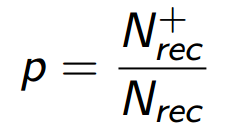
Зато, как мы увидим чуть позже, это деление позволит учесть в метрике очень существенный аспект задачи — зависимость метрики от порядка рекомендаций в списке. Кроме того, у значения p есть понятная логика, которую можно описать вероятностным языком. Допустим, что человек потребляет наш продукт, а именно, просматривает все элементы списка рекомендаций. Тогда p означает для него вероятность найти в этом списке подходящий элемент — такой, который удовлетворит его в относительном будущем. Обозначим precision для пользователя u как p_u:


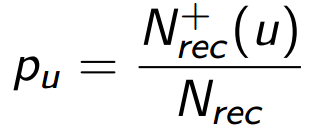
Уместно обобщить эту формулу на всю нашу аудиторию (или измеряемую выборку) пользователей (Users):


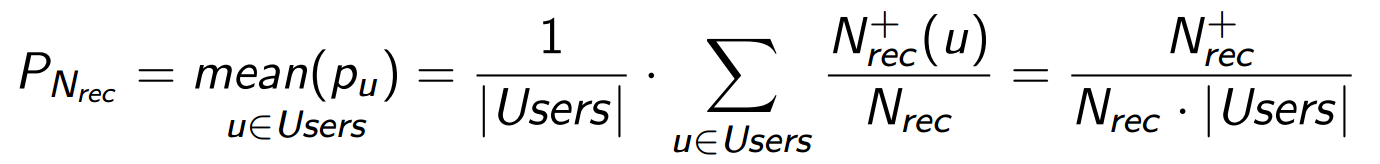
Каждый смотрит свой собственный список и выбирает то, что ему нужно, а P_Nrec показывает среднюю вероятность успеха для всех случаев. Значение в правой части — это теперь общее количество успехов во всей выборке.

Дисконтирование

До сих пор мы оценивали список элементов как целое, но мы прекрасно знаем, что его начало важнее, чем хвост. Во всяком случае, если список не слишком короткий. Метрика, которая это учитывает, а значит зависит от порядка элементов в списке, называется дисконтированной. Начало списка важнее, чем хвост, из-за неравномерного распределения внимания пользователей — люди почти всегда смотрят на первый элемент, несколько реже смотрят и на первый и на второй и т.д. Это значит, что для правильного дисконтирования нам нужна некоторая поведенческая модель. И данные, которыми мы эту модель можем поддержать (обучить).

Мы представляем себе усреднённого пользователя, который просматривает элементы по очереди, начиная с первого, а затем, в определённый момент, перестает это делать:


Мы не можем идентифицировать конкретного пользователя, да и не хотим. Иногда один и тот же человек захочет просмотреть список из 2 элементов, а иногда из 20.

Было бы неплохо раздобыть средние вероятности перехода от каждого элемента к следующему, но нам хватит данных даже немного попроще.

Допустим, что у нас есть вероятность того, что произвольный человек просмотрит список длинной N элементов: w_N для любого разумного N. Тогда можно по формуле полной вероятности усреднить значения P_N, понимая под P_N среднее значение вероятности успеха именно для той части нашей аудитории, которая просмотрела список длиной N. В нашей терминологии это будет выглядеть так:


Получается, что в отличие от precision, значение AUC оценивает среднюю вероятность успеха персональных рекомендательных списков в более реальных условиях — когда списки просматривают живые люди, внимание которых распределено неравномерно. Заметим, что чтобы получить величину AUC, мы использовали зависимость величины P_Nrec (precision) от N_rec — размера списка рекомендаций, который чуть раньше мы фиксировали.

Что такое AUC?

Термином AUC обозначают, в том числе, и интеграл precision by recall, который используется иногда как метрика качества классификаторов.

Суммирование, которое мы сделали, — это в каком-то смысле аналог такой метрики: разными значениями N_rec мы моделируем разные значения Recall.



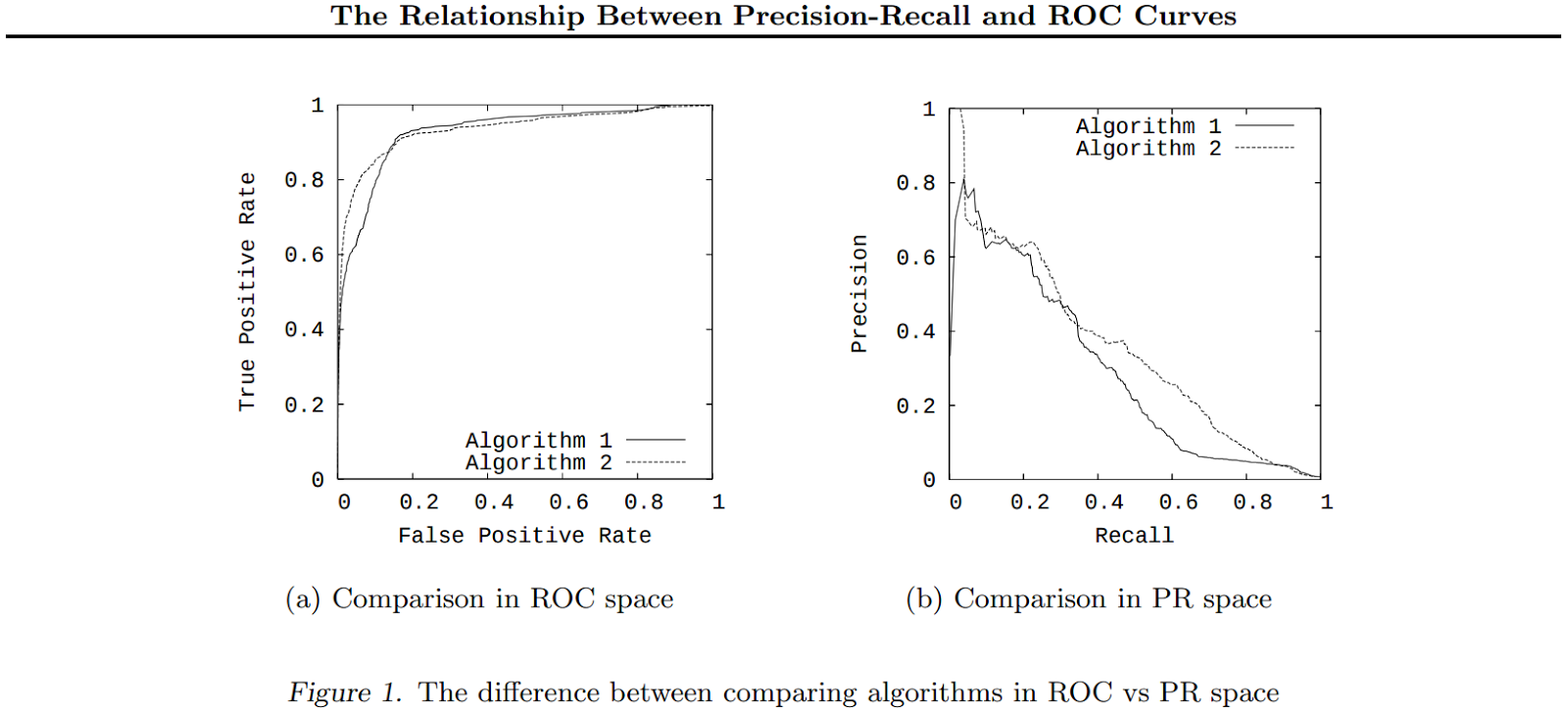
Это (уже классический) пример построения ROC-кривых в координатах precision-recall

Как быстро оценить значение весов wN?

Есть простая и распостранённая модель оценки значений w_N, которая позволяет не обрабатывать всё распределение вероятностей переходов, но даёт качественно правильное поведение значений w_N:


Единственный параметр модели Q — вероятность того, что произвольный пользователь перейдет на следующую страницу списка (его легко получить из веб-логов пагинации). Допустим, что страницы содержат по m элементов, а пользователи с одной и той же вероятностью p переходят к просмотру следующего элемента или, другими словами, с вероятностью (1-p) на каждом элементе уходят. Тогда p легко получить из соотношения Q = p^m. (Если предположить, что первый элемент будет просмотрен с вероятностью 1.) Тогда, нужную нам вероятность w_N, что человек посмотрит N элементов, а после этого уйдёт, легко вычислить:


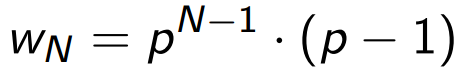
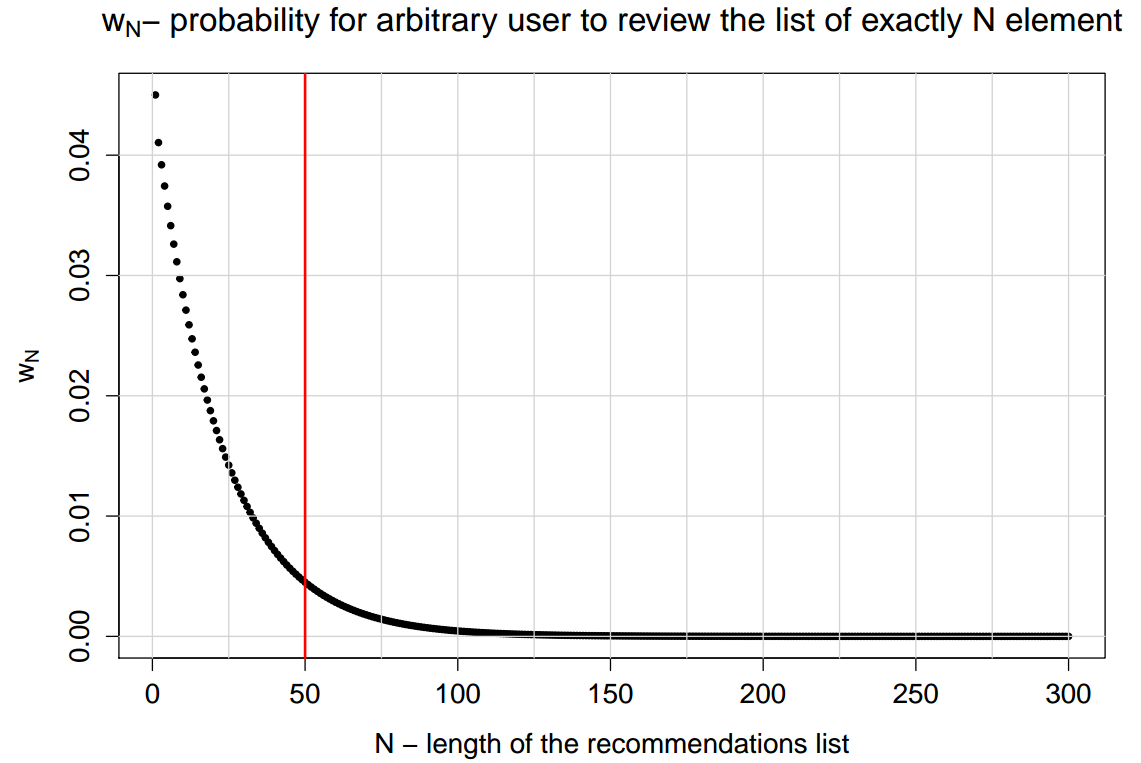
В нашем эксперименте страницы состояли из 50 элементов, а значение Q оказалось равным 0.1. Зависимость w_N от N при этом выглядит вот так:

Значение оценки и «удовлетворённость»

До сих пор мы пользовались только фактом позитивного сигнала и игнорировали то, что у нас есть его величина. Ясно, что пренебречь этой информацией было бы несправедливо. Когда шкала сбора оценок выбрана хорошо, величина сигнала должна быть, в среднем, пропорциональна удовлетворённости человека:


Следуя этой логике, заменим в текущей метрике:


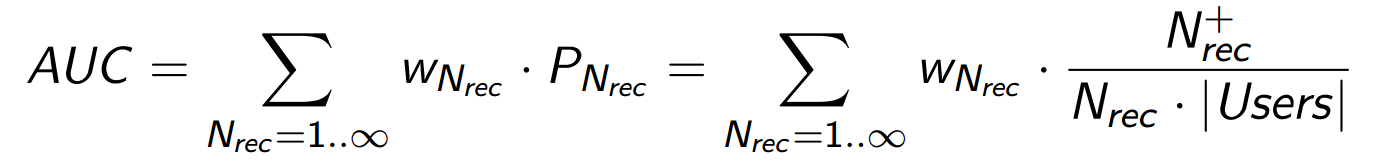
… счётчик успехов на (более информативную) сумму положительных баллов:


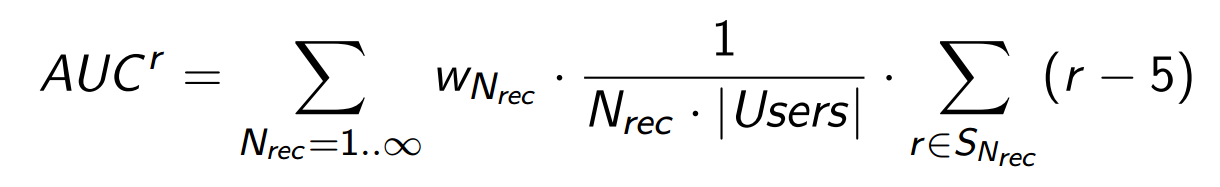
S_Nrec — множество успешных оценок, то есть тех позитивных оценок, которые посчитаны в . Позитивная часть нашей шкалы начинается с 6-ти баллов, поэтому мы (просто для удобства) вычитаем 5 из всех оценок r.

Почему можно так сделать? Потому, что можно представить роль позитивных баллов в метрике немного по-другому:


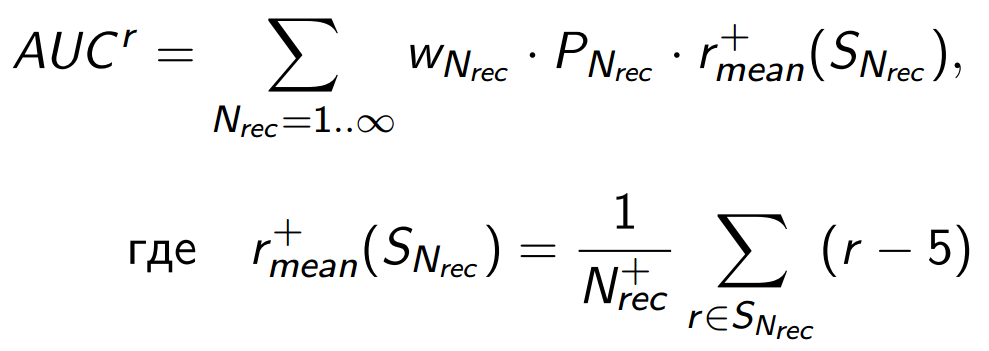
это средний позитивный балл по той аудитории, которая просмотрит список длинной N_rec. А поскольку мы предполагали, что списки разной длинны просматривают примерно одни и те же люди, то увеличение метрики будет зависеть только от способности алгоритма увеличивать средний балл для верхней части списков за счет нижней для всех пользователей.

Произведение вероятности успеха на средний балл в случае успеха вполне можно назвать общим объемом удовлетворённости, которого может достичь рекомендательный алгоритм. То есть теперь метрика, хотя и теряет чисто вероятностную интерпретацию, но лучше подходит нашим целям. (Заметим, что численное значение AUC^r может быть любым — по сути, это удельное количество позитивных баллов в фидбэке, которое зависит от размера выборки, активности аудитории, выбранной поведенческой модели пользователей и т.д.)

Допустим, что два рекомендательных алгоритма сгенерировали топ-листы, немного отличающиеся порядком элементов. Оказалось, что в первом случае фактические оценки пользователя распределились вот так:


а во втором так:


Одновременный учёт и величины оценки и дисконтирование позволяют AUC^r обоснованно и количественно их различить, то есть обнаружить, что второй алгоритм лучше и сказать насколько.

Long tail and short head

Кинофильмы, как и другие медиа-продукты, имеют забавную особенность: распределение элементов по популярности экстремально неравномерно, cуществует совсем немножко фильмов, которые известны и оцениваются большим количеством людей, — это short head, а подавляющее большинство известно относительно немногим — это long tail.

Например, распределение оценок imhonet выглядит вот так:


Это распределение настолько крутое в части short head, что при любом суммировании сигналов фильмы из него доминируют, давая более 80% вклада в метрику. Это вызывает её численную неустойчивость: исчезновение или появление в топе рекомендаций всего нескольких объектов из short head может драматически изменить величину метрики.

Опережая ваше любопытство, заметим, что особенность short-head-части графика можно спрямить в log-log координатах:

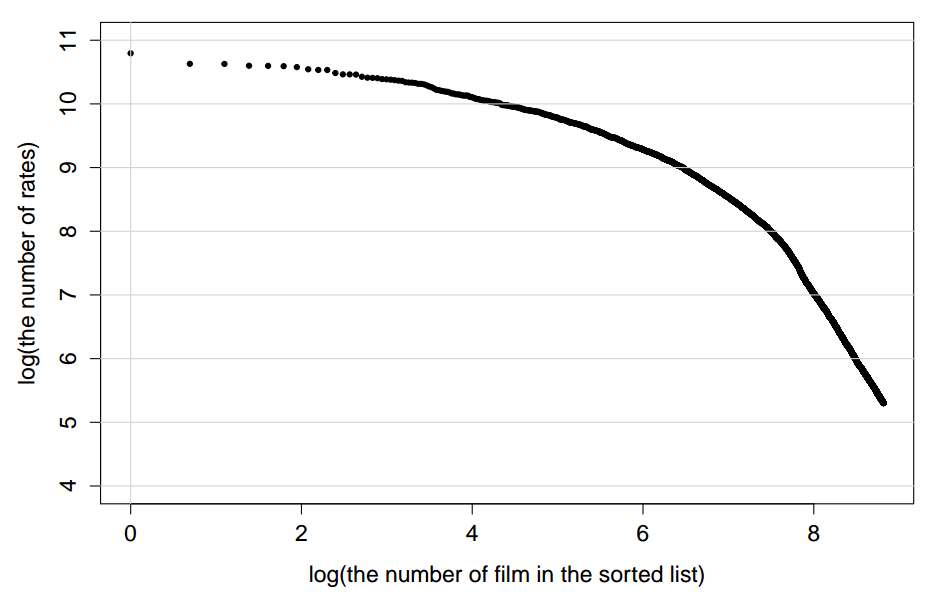
Такие координаты используются, например, для описания распределения частотности слов в естественных языках.

Вспомним, что цель рекомендательных систем — это эффективная персонализация. Она связана с умением точно
выбирать элементы из long tail. Элементы из short head, в основном, и так всем известны, то есть почти не нуждаются во включении в рекомендации:


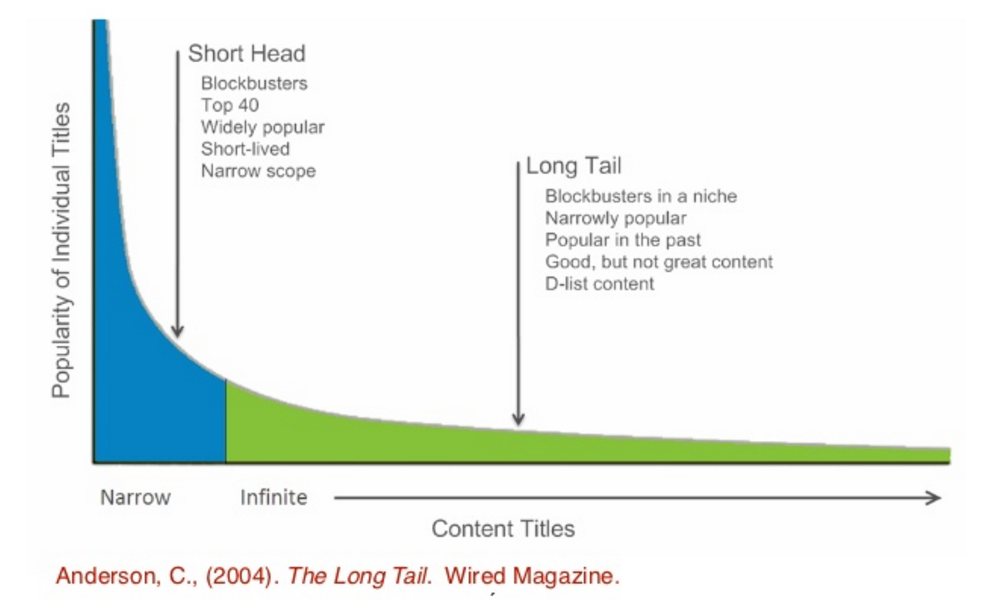
Поэтому здравое решение — просто уменьшить вес short head в метрике. Как сделать это корректно? Отталкиваемся от, собственно, проблемы метрики — численная неустойчивость обязательно приведет к снижению чувствительности. Смоделируем тестовые случаи, которые метрика обязана различать и добьёмся её максимальной чувствительности в них. Как точку отсчета возьмем ситуацию, когда мы не знаем про пользователей из нашей выборки ничего. Тогда все персональные списки рекомендаций получатся одинаковыми и будут соответствовать некоторому кинорейтингу. Для построения этого кинорейтинга используем простую вероятность, что фильм понравится, вычисленную на всей базе оценок. Например, это может быть вероятность, что произвольная оценка фильма больше, чем 5 баллов:


(Для расчетов, мы, конечно, скорректируем эту вероятность по правилу Лапласа. И можем учесть величины оценок.)

К счастью, кроме оценок, мы знаем про пользователей из нашей выборки разную дополнительную информацию, которую они указывает в анкете: пол, возраст, любит фантастику или наоборот, и многое другое. Например, мы знаем пол. Тогда мы можем построить вместо одного общего два разных рекомендательных списка. Мы сделаем это, пользуясь Байесовской формулой вероятности:


Здесь вероятность для нашей точки отсчета P(r>5) работает как априорная. Так как два разных рекомендательных списка лучше, чем один, мы вправе ожидать прироста значения метрики:



Удобнее оценивать относительный прирост:


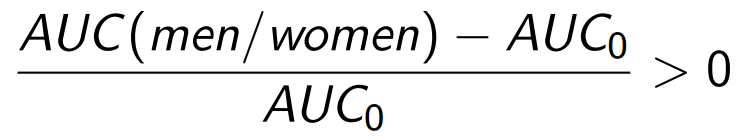
Увеличение метрики должно происходить и при использовании любой другой информации о пользователях, существенной для кинопредпочтений. Чем больше оказывается прирост, тем значит чувствительнее она к этой информации. Поскольку нас интересует не конкретный случай про пол, то чтобы не переобучиться именно на нем, мы усредним прирост AUC по множеству доступных нам способов разделить аудиторию. В нашем эксперименте использовались ответы пользователей в анкете на 40 разных вопросов.

А теперь выпишем, как выглядит оптимизационная задача, которая находит нужную нам метрику, обладающую оптимальной чувствительностью. Вспомним, что базовая идея — уменьшение веса для элементов из short head. Функцию, отвечающую за штрафы short head для элементов, обозначим ?. Нам нужна такая функция ?, которая обеспечивает максимум чувcтвительности:


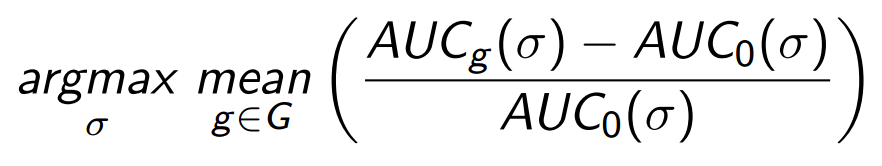
Здесь G — множество способов сегментации аудитории с соответствующими расчетами рекомендаций для сегментов.

В простом эксперименте, который оказался действенным, мы использовали в качестве ? ступенчатую функцию (аппроксимацию сигмоиды), которая просто обнуляет веса для short head:


Это значит, что оптимизационную задачу:


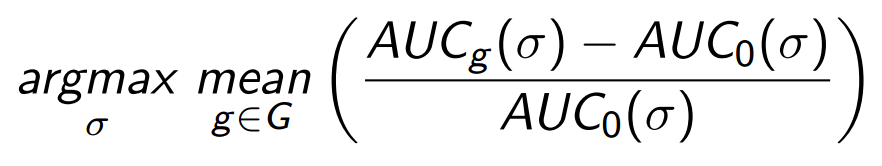
нужно решить для единственного параметра ?, который определяет положение ступеньки в списке фильмов, отсортированном по количеству оценок. Например, вот что получилось при оптимизации у нас:


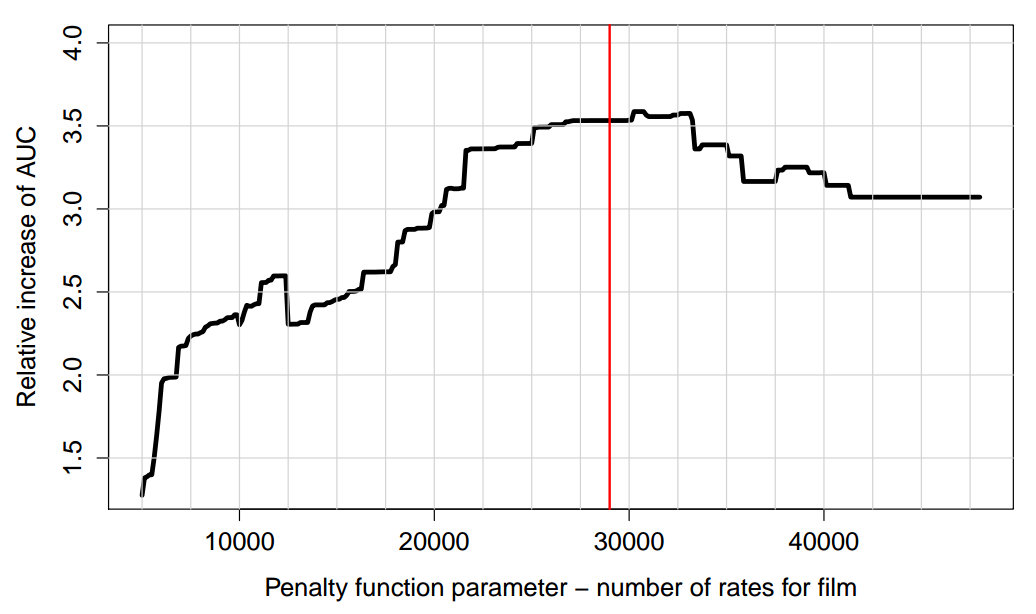
На левом крае — штрафуем слишком много элементов. На правом — никого не штрафуем. В оптимальном положении (40 фильмов оштрафовано) чувствительность метрики улучшается на ~20%.

Резюме: расчетная формула

Приведем окончательную форму метрики, которая принимает во внимание всю вышеописанную логику. Метрика AUC^r, которая:

• измеряет качество персональных списков рекомендаций по оценкам пользователей, сделанным постфактум, как вероятность, что рекомендация будет успешна (precision);
• чувствительна к порядку элементов в списках или, точнее говоря, дисконтирована в соответствии с простой поведенческой моделью — просмотром рекомендаций пользователем по очереди и сверху вниз;
• учитывает значения позитивных оценок, поэтому может измерить не просто концентрацию успехов, но и объем удовлетворённости;
• корректно обрабатывает проблему short head/long tail — штрафует элементы short head таким образом, чтобы оптимизировать чувствительность;

может быть записана следующим образом:

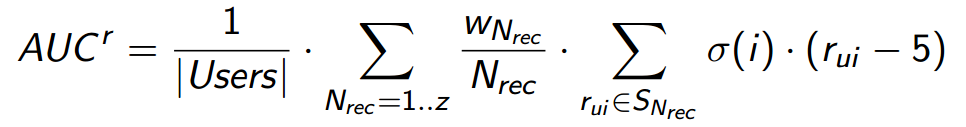
• N_rec — длина списков рекомендаций
  
• z — ограничение для суммирования значений precision. Для длинных списков значения precision очень малы, также как и множитель WN_rec, поэтому достаточно большое z не влияет на метрику, и выбрать его несложно,
• |Users| — сколько пользователей в выборке,
• WN_rec — оценка вероятности, что случайный пользователь просмотрит список длиной ровно N_rec,
  
• S_Nrec — множество успешных оценок, если списки рекомендаций имеют длину N_rec,
• ?(i) — значение штрафной функции (short-head) для элемента i,
• r_ui — оценка, которую получил элемент i от пользователя u.

Отметим здесь еще один интересный момент. Вcе пользователи со своими оценками входят в формулу для AUC^r равноправно. Однако мы знаем, что иногда люди могут пользоваться шкалой оценок по-разному — одни могут ставить очень много высоких баллов, другие наоборот — редко дают высокие баллы. Значит, если использовать в метрике непосредственные значения оценок r, то вклад от первых пользователей будет выше за счет уменьшенного вклада от вторых. Выход — ввести нормализованную шкалу, в которой оценки, сделанные разными типами пользователей, будут сравнимы между собой. На практике, однако, оказалось, что когда мы работаем с большой выборкой, этим эффектом можно пренебречь. Основная причина в том, что тип использования шкалы не коррелирует со вкусом человека, поэтому усреднение по аудитории, которое происходит при расчете AUC^r, оказывает такой же эффект, как использование нормализованной шкалы.

Несколько примеров из практики

Приведём несколько практических примеров использования метрики. Мы пользовались моделями машинного обучения рекомендательной системы imhonet.ru, детали применения которых тут опускаем — просто показываем результаты решения задач, в которых целевой метрикой являлся AUC^r. Особенную проблему для рекомендательных систем представляют задачи холодного старта. Они бывают у нас двух типов:

• Новичок. Нужно побыстрее начать считать ему точные рекомендации.
• Новинка. Нужно побыстрее начать точно рекомендовать элемент пользователям.

Чем больше человек поставил оценок, тем точнее его списки рекомендаций. Сопоставим эту зависимость (красная линия) со значением метрики, которое дает общий рейтинг (AUC₀, черная линия), и с тем уровнем, когда мы даем рекомендации, используя только пол и возраст (оранжевая линия):

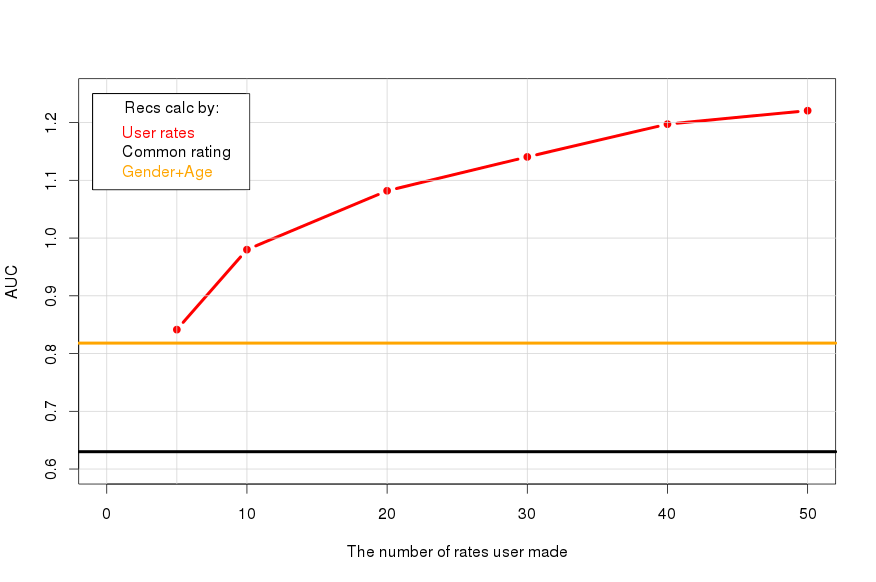
Информация про пол и возраст даёт примерно столько же, сколько 5 оценок.

Вопросник. Для обычного человека не всегда просто сформулировать свои предпочтения сразу в виде оценок элементам, поэтому для новичков мы предлагаем отвечать на простые вопросы, например «Любите ли вы аниме?», «Любите ли вы экшн?». Для этой цели мы завели несколько сотен таких вопросов. Посмотрим, что может дать их использование:

Вопросы получаются не так информативны, но все равно выгодны, так как отвечать значительно проще, чем ставить числовые оценки. Например, 10 оценок эквивалентны 25 ответам.

Рекомендации по профилю из другого раздела. Бывает так, что человек уже составил свой профиль из оценок элементов другого раздела. Если между предпочтениями в разных разделах есть связь, это можно пытаться использовать. В нашем примере по профилям оценок художественных книг мы пытаемся давать рекомендации кино:

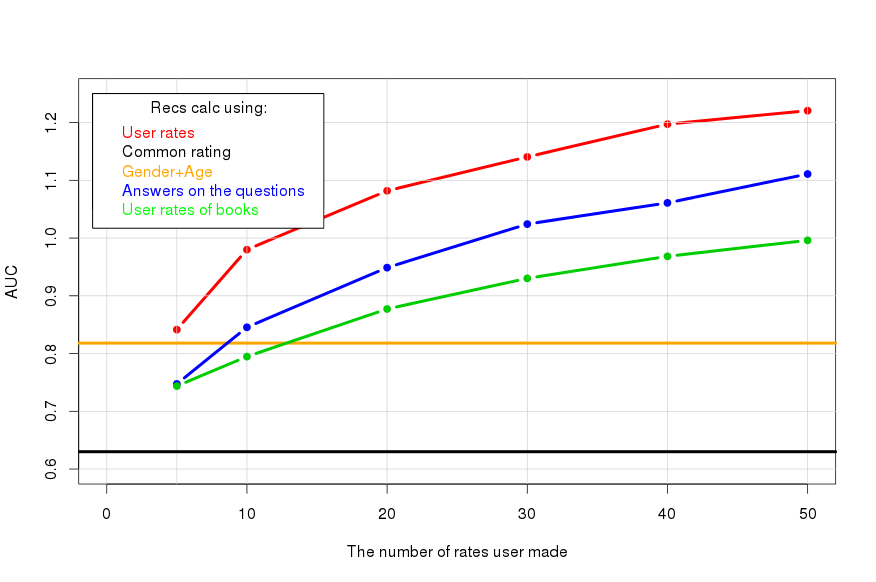
Получается хуже чем использование вопросов, но определённый эффект зафиксировать можно.

Новинки. Очень-очень нужно уметь начинать рекомендовать новинки до того, как их начнут оценивать пользователи. Ясно, что это можно сделать только на основе исходящих данных про фильм. В нашей рекомендательной системе свойствами фильмов, которые ключевым образом влияют на рекомендации, оказались:

• Жанры
• Режиссеры
• Актеры
• Сценаристы

Эти метаданные позволяют начать рекомендавать фильм так, как будто «хорошие» пользователи (не новички) уже поставили ему примерно 27 оценок:

Это неплохо.

Спасибо за внимание!