
Нейронные сети – один из самых популярных классов алгоритмов для машинного обучения. В финансовом анализе они чаще всего применяются для прогнозирования, создания собственных индикаторов, алгоритмического трейдинга и моделирования рисков. Несмотря на все это, репутация у нейронных сетей подпорчена, поскольку результаты их применения можно назвать нестабильными.
Количественный аналитик хедж-фонда NMRQL Стюарт Рид в статье на сайте TuringFinance попытался объяснить, что это означает, и доказать, что все проблемы кроются в неадекватном понимании того, как такие системы работают. Мы представляем вашему вниманию адаптированный перевод его статьи.
1. Нейронная сеть – это не модель человеческого мозга
Человеческий мозг – одна из самых больших загадок, над которой бьются ученые не одно столетие. До сих пор нет единого понимания, как все это функционирует. Есть две основные теории: теория о «клетке бабушки» и теория дистрибутивного представительства. Первая утверждает, что отдельные нейроны имеют высокую информационную вместимость и способны формировать сложные концепты. Например, образ вашей бабушки или Дженнифер Энистон. Вторая говорит о том, что нейроны намного проще в своем устройстве и представляют комплексные объекты лишь в группе. Искусственную нейронную сеть можно в общих чертах представить как развитие идей второй модели.
Огромная разница ИНС от человеческого мозга, помимо очевидной сложности самих нейронов, в размерах и организации. Нейронов и синапсов в мозгу несоизмеримо больше, они самостоятельно организуются и способны к адаптации. ИНС конструируют как архитектуру. Ни о какой самоорганизации в обычном понимании не может быть речи.
Что из этого следует? ИНС создаются по архетипу человеческого мозга в том же смысле, как олимпийский стадион в Пекине был собран по модели птичьего гнезда. Это ведь не означает, что стадион – это гнездо. Это значит, что в нем есть некоторые элементы его конструкции. Лучше говорить о сходстве, а не совпадении структуры и дизайна.
Нейронные сети, скорее, имеют отношение к статистическим методам – соответствия кривой и регрессии. В контексте количественных методов в финансовой сфере заявка на то, что нечто работает по принципам человеческого мозга, может ввести в заблуждение. А в неподготовленных умах вызвать страх угрозы вторжения роботов и прочую фантастику.
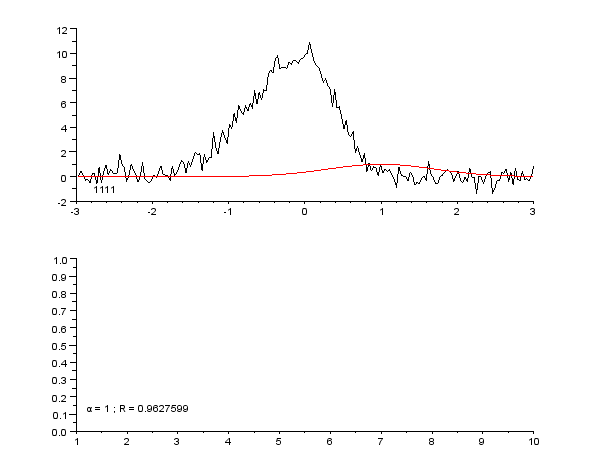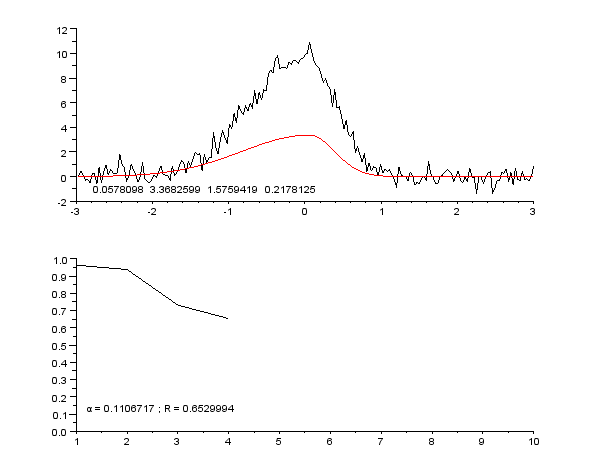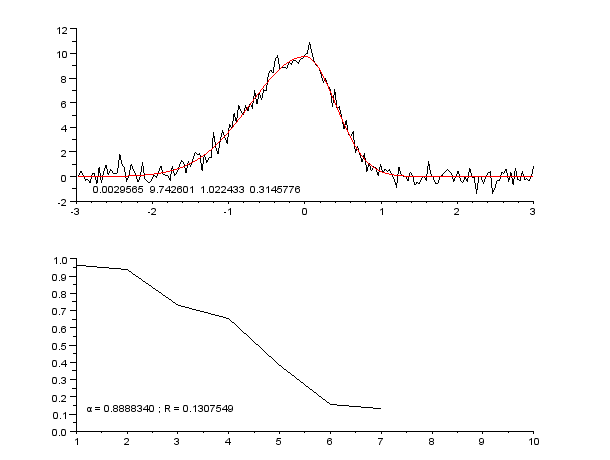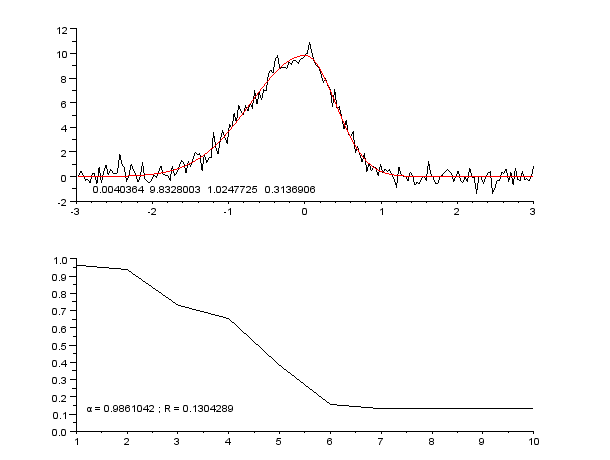
Пример кривой, также известной как функция приближения. Нейронные сети очень часто используют для аппроксимации сложных математических функций
2. Нейронная сеть – не упрощенная форма статистики
Нейронные сети состоят из слоев соединенных между собой узлов. Отдельные узлы называются перцептронами и напоминают множественную линейную регрессию. Разница в том, что перцептроны упаковывают сигнал, произведенный множественной линейной регрессией, в функцию активации, которая может быть как линейной, так и нелинейной. В системе со множеством слоев перцептронов (MLP) перцептроны организованы в слои, которые в свою очередь соединены друг с другом. Есть три типа слоев: слои входных данных и выходных сигналов, скрытые слои. Первый слой получает паттерны входных данных, второй может поддерживать список классификации или сигналы вывода в соответствии со схемой. Скрытые слои регулируют веса входных данных, пока риски ошибки не сводятся к минимуму.
Картирование инпутов/аутпутов
Перцепторы получают векторы входных данных — z=(z1,z2,…,zn) из n атрибутов. Вектор называется входным паттерном (input pattern). Вес такого «инпута» определяется весом вектора, принадлежащего к этому перцептрону — v=(v1,v2,…,vn). В контексте множественной линейной регрессии это можно представить как коэффициент регрессии. Сигнал перцептрона в сети, net, обычно складывается из входного паттерна и его веса.
net=?nizivi
Сигнал минус смещение ? затем преобразуется в некую активационную функцию. Обычно это монотонно возрастающая функция с границами (0,1) или (-1,1). Некоторые наиболее популярные функции представлены на картинке:
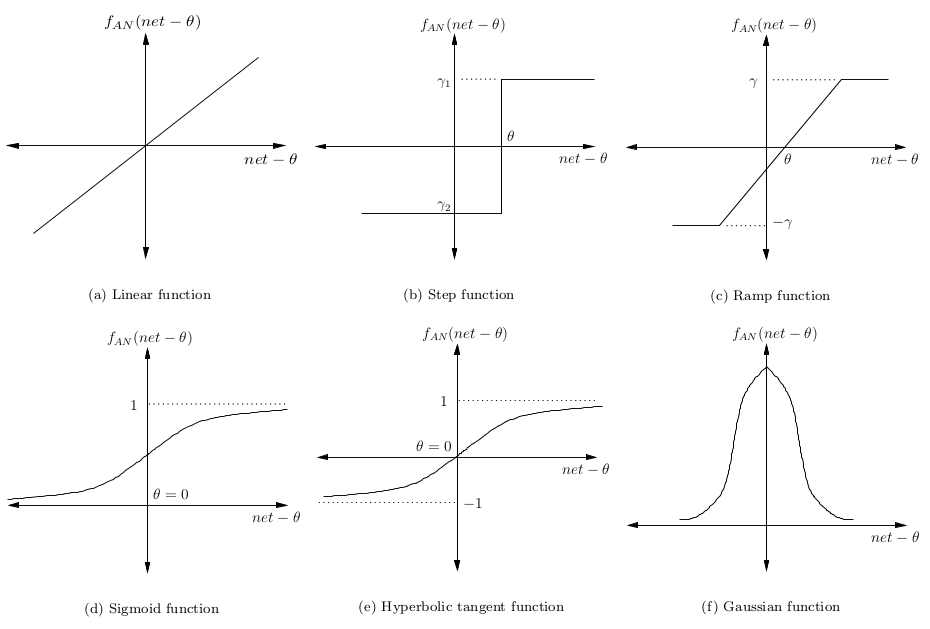
Простейшая нейронная сеть – так, которая имеет лишь один нейрон, картирующий входные сигналы в выходные.
Создание слоев

Как видно из рисунка, перцептроны организованы в слои. Первый слой, который позже получит название входного, получает паттерн p в процессе обучения – Pt. Последний слой привязан к ожидаемым выходным сигналам для этих паттернов. Паттерны могут быть величинами разных технических индикаторов, а потенциальные выходные сигналы могут быть категориями {BUY,HOLD,SELL}.
Скрытый слой – тот, который получает инпуты и аутпуты от другого слоя и формирует аутпуты для следующего. По одной из версий, скрытые слои извлекают выступающие элементы из входящих данных, которые имеют значение для предсказания результата. В статистике такая техника зовется первичным компонентным анализом.
Глубокая нейронная сеть имеет большое количество скрытых слоев и способна извлекать больше подходящих элементов данных. Недавно их с успехом использовали для решения проблем распознавания образов.
В задачах трейдинга при использовании глубоких сетей есть одна проблема: данные на входе уже подготовлены и может быть сразу несколько элементов, которые необходимо извлечь.
Правила обучения
Задача нейронной сети минимизировать степень ошибки ?. Обычно этот показатель рассчитывается как сумма квадратов ошибок. Хотя такой вариант может быть чувствителен к постороннему шуму.

Для наших целей мы можем использовать алгоритм оптимизации, чтобы приспособить показатели веса к сети. Чаще всего для обучения сети применяют алгоритм градиентного спуска. Он работает через калькуляцию частичных дериватов ошибок с учетом их веса для каждого слоя и затем двигается в обратном направлении по уклону. Минимизируя ошибку, мы увеличиваем производительность сети в выборке.
Математически это правило обновления можно выразить в следующей формуле:
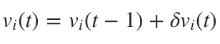 , где
, где  , где
, где
? – частота обучения, отвечающая за то, как быстро или медленно сеть конвергируется. Выбор частоты обучения имеет серьезные последствия в плане производительности нейронной сети. Маленькое значение приведет к медленной конвергенции, большое может привести к отклонениям в обучении.
Итак, нейронная сеть – это не есть упрощенная форма статистики для ленивых аналитиков. Это некая выдержка серьезных статистических методов, применяемых уже сотни лет.
3. Нейронная сеть может быть исполнена в разной архитектуре
До этого момента мы рассуждали о самой примитивной архитектуре нейронной сети – системе многоуровневых перцептронов. Есть еще множество вариантов, от которых зависит производительность. Современные достижения в изучении машинного обучения связаны не только с тем, как работают оптимизационные алгоритмы, но как они взаимодействуют с перцептронами. Автор предлагает рассмотреть наиболее интересные, с его точки зрения, модели.
Рекуррентная нейронная сеть: у нее некоторые или все соединения отыгрывают назад. По сути, это принцип технологии Feed Back Loop (уведомление провайдера сервису рассылки при наборе критического числа жалоб на спам). Считается, что такая сеть лучше работает на серийных данных. Если так, то этот вариант вполне уместен в отношении финансовых рынков. Для более подробного ознакомления нам предлагают почитать вот эту статью.
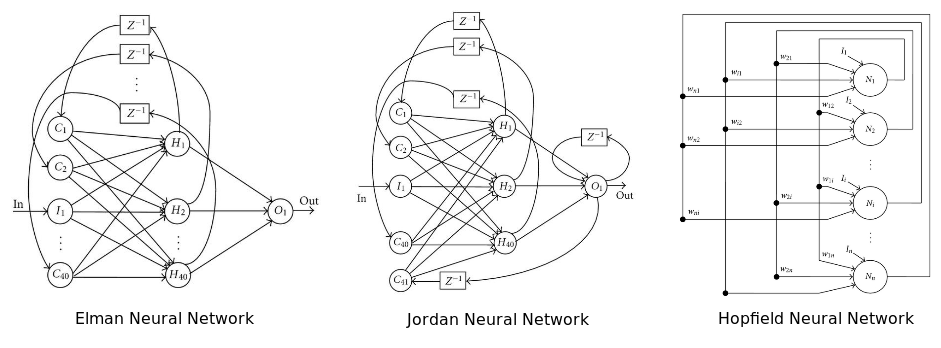
На диаграмме изображены три популярных архитектуры нейронных сетей
Последний из придуманных вариантов архитектуры рекуррентной нейронной сети – нейронная машина Тьюринга. Она объединяет архитектуру стандартной сети с памятью.
Нейронная сеть Больцмана – одна из первых полностью связанных нейронных сетей. Она одной из первых была способна обучаться внутренним представлениям и решать сложные задачи по комбинаторике. Про нее говорят, что это версия Монте-Карло рекуррентной нейронной сети Хопфилда. Ее сложнее обучать, но если поставлены ограничения, то она эффективней традиционной сети. Самое распространенное ограничение в отношении сети Больцмана – запрет на соединения между скрытыми нейронами. Собственно, еще один вариант архитектуры.
Глубокая нейронная сеть – сеть со множеством скрытых слоев. Такие сети стали крайне популярны в последние годы, из-за их способности с блеском решать проблемы по распознаванию голоса и изображения. Число архитектур в данном варианте растет небывалыми темпами. Самые популярные: глубокие сети доверия, сверточные нейронные сети, автокодировщики стэка и прочее. Самая главная проблема с глубокими сетями, особенно в случае с финансовым анализом, — переобучение.
Адаптивная нейронная сеть одновременно адаптирует и оптимизирует архитектуру в процессе обучения. Она может наращивать архитектуру (добавлять нейроны) или сжимать ее, убирая ненужные скрытые нейроны. По мнению автора, эта сеть лучше всего подходит для работы на финансовых рынках, потому что сами эти рынки не стационарны. То есть сеть способна подстраиваться под динамику рынка. Все, что было здорово вчера, не факт, что будет оптимально работать завтра.
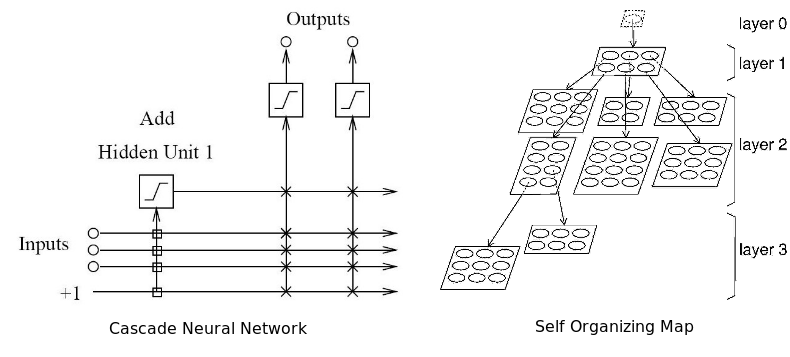
Два типа адаптивных нейронных сетей: каскадная и самоорганизующаяся карта
Радиально-базисная сеть – не то чтобы отдельный тип архитектуры в плане размещения соединений и перцептронов. Здесь в качестве активирующей функции используется радиально-базисная функция, чьи аутпуты зависят от расстояния от конкретной точки. Самое распространенное применение этой функции – гауссовское распределение. Она также используется как ядро в векторной машине поддержки.
Проще всего – попробовать несколько вариантов на практике и выбрать наиболее подходящий под конкретные задачи.
4. Размер имеет значение, но больше – не всегда значит лучше
После выбора архитектуры возникает вопрос, насколько большой или насколько небольшой должна быть нейронная сеть? Сколько должно быть «инпутов»? Сколько нужно использовать скрытых нейронов? Скрытых слоев (в случае с глубокой сетью)? Сколько «аутпутов» нужно нейронам? Если мы промахнемся с размером, сеть может пострадать от переобучения или недообучения. То есть не будет способна грамотно обобщать.
Сколько и какие инпуты нужно использовать?
Число входных сигналов зависит от решаемой проблемы, количества и качества доступной информации и, возможно, некоторой доли креатива. Выходные сигналы – это простые переменные, на которые мы возлагаем некие предсказательные способности. Если входные данные к проблеме не ясны, можно определять переменные для включения через систематический поиск корреляций и кросс-корреляций между потенциальными независимыми переменными и зависимыми переменными. Этот подход детально рассматривается в этой статье.
С использованием корреляций есть две основные проблемы. Во-первых, если вы используете метрику линейной корреляции, вы можете непреднамеренно исключить нужные переменные. Во-вторых, две относительно не коррелированных переменных могут быть потенциально объединены для получения одной хорошо коррелированной переменной. Когда вы смотрите на переменные изолировано, вы можете упустить эту возможность. Здесь можно использовать основной компонентный анализ для извлечения полезный векторов в качестве входных сигналов.
Другая проблема при выборе переменных – мультиколлинеарность. Это когда две или более переменных, загруженных в модель, имеют высокую корреляцию. В контексте регрессивных моделей это может вызвать хаотичные изменения регрессивного коэффициента в ответ на незначительные изменения в модели или в данных. Учитывая то, что нейронные сети и регрессионные модели схожи, можно предположить, что та же проблема распространяется на нейронные сети.
Еще один момент связан с тем, что за выбранные переменные принимают пропущенные отклонения в переменных. Они появляются, когда модель уже сформирована, а за бортом осталась парочка важных каузальных переменных. Отклонения проявляют себя, когда модель получает неверное возмещение отсутствующим переменным через переоценку или недооценку других переменных.
Сколько необходимо скрытых нейронов?
Оптимальное число скрытых элементов – специфическая проблема, решаемая опытным путем. Но общее правило: чем больше скрытых нейронов – тем выше риск переобучения. В этом случае система не изучает возможности данных, а как бы запоминает сами паттерны и любой содержащийся в них шум. Такая сеть отлично работает на выборке и плохо за пределами выборки. Как можно избежать переобучения? Есть два популярных метода: ранняя остановка и регуляризация. Автор предпочитает свой, связанный с глобальным поиском.
Ранняя остановка предполагает разделение процесса обучения на этапы самого обучения и валидации результатов. Вместо того чтобы обучать сеть на ограниченном числе итераций, вы обучаете ее пока производительность сети на этапе подтверждения не начинает падать. По-существу, это не дает сети использовать все доступные параметры и ограничивает способности к простому запоминанию паттернов. Ниже показаны две возможные точки остановки:
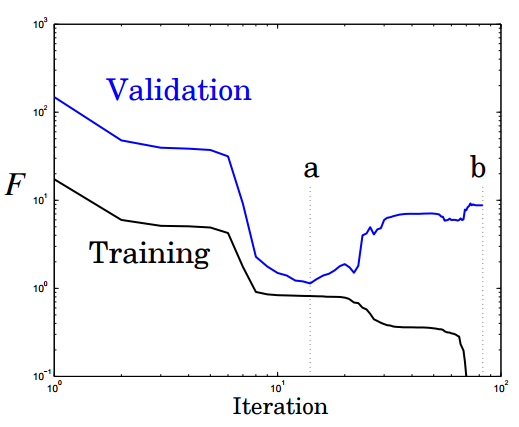
Еще одна картинка показывает производительность и степень переобучение сети при остановке в этих точках a и b:
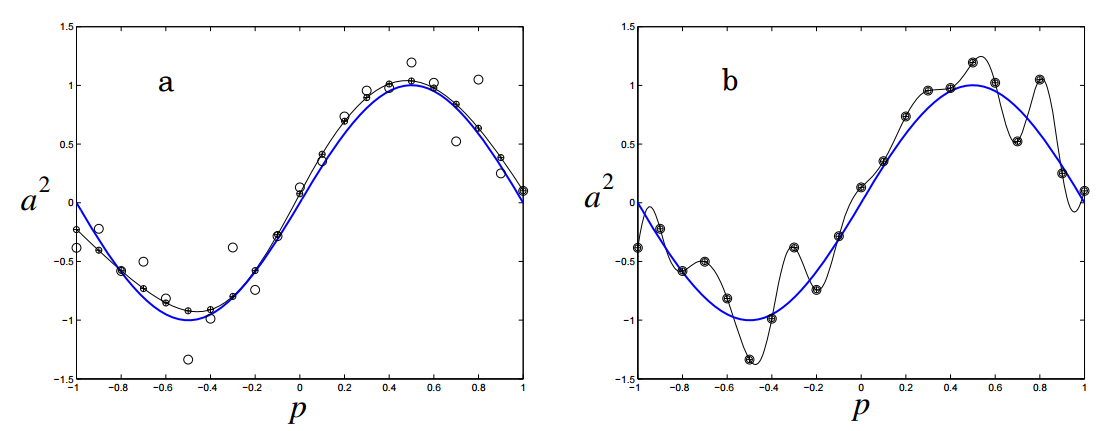
Регуляризация штрафует нейронную сеть за использования усложненной архитектуры. Сложность в данном случае измеряется размером и весом сети. Она устанавливается через добавление интервала к функции ошибки, который привязан к весу и размеру. Это то же самое, что добавление приоритета, который заставляет поверить нейронную сеть функцию на однородность.

n- это число нагрузок (весов) в нейронной сети. Параметры ? и ? контролируют уровень, после которого наступает недообучение или переобучение сети. Подходящие значения для них можно подобрать через Байесовский анализ и оптимизацию.

Другая техника, довольно дорогостоящая в плане вычислений, — глобальный поиск. Здесь алгоритм поиска используется для дифференциации архитектуры сети и нахождения ее оптимального варианта. Обычно для этого берут алгоритм генерации, о котором будет сказано ниже.
Что такое «аутпуты»?
Нейронную сеть можно использовать для регрессии или классификации. В первой модели мы работаем с единичным значением на выходе. То есть нужен всего один нейрон выхода. Во второй модели нейрон выхода нужен для каждого класса, к которому может принадлежать паттерн, в отдельности. Если классы не известны – используются самоорганизующиеся карты.
Подытожим эту часть рассказа. Лучший подход для определения размера сети – следовать принципу Оккама. То есть для двух моделей с одинаковой производительностью, модель с меньшим количеством параметров будет генерализировать успешней. Это не значит, что нужно обязательно выбирать простую модель в целях повысить производительность. Верно обратное утверждение: множество скрытых нейронов и слоев не гарантирует превосходство. Слишком много внимание сегодня уделяется большим сетям, и слишком мало самим принципам их разработки. Больше – не всегда лучше.
5. К нейронной сети применимо множество обучающих алгоритмов
Обучающий алгоритм призван оптимизировать вес нейронной сети, пока не наткнется на некое условие остановки. Это может быть связано с появлением ошибки в тренировочном сете на приемлемом уровне точности (например, когда работа сети на этапе валидации начинает ухудшаться). Это может быть точка, когда израсходован некий вычислительный бюджет сети. Самый популярный вариант алгоритма – метод обратного распространения с использованием градиентного стохастического спуска. Обратное распространение состоит из двух шагов:
- Прямое прохождение: обучающие данные проходят через сеть, записывается выходной сигнал и подсчитываются ошибки.
- Обратное распространение: сигнал ошибки протаскивается обратно через сеть, вес сети оптимизируется с использованием градиентного спуска.
С этим подходом может возникнуть несколько проблем. Подгонка всех весов одновременно может привести к чрезмерному перемещению сети в весовом пространстве. Алгоритм градиентного спуска довольно медленный и восприимчив к локальному минимуму. Локальный минимум – специфическая проблема для определенных нейронных сетей. Первая проблема решаема через использования разных вариантов градиентного спуска: (QuickProp), Nesterov's Accelerated Momentum (NAG), Adaptive Gradient Algorithm (AdaGrad), Resilient Propagation (RProp) или Root Mean Squared Propagation (RMSProp).

Но все эти алгоритмы не могут преодолеть локальный минимум, и менее полезны, когда пытаются одновременно оптимизировать архитектуру и нагрузку сети. Нужен алгоритм глобальной оптимизации. Это может быть метод роя частиц (Particle Swarm Optimization) или генетический алгоритм. Вот, как это работает.
Векторное представление нейронной сети кодирует нейронную сеть по вектору нагрузки, каждый из векторов представляет вес соединения в сети. Мы можем обучать сеть, используя мета-эвристический поисковой алгоритм. На слишком больших сетях метод работает плохо, потому что сами векторы становятся слишком большими.

На диаграмме показано, как нейронная сеть может быть представлена в векторной нотации
Метод роя частиц обучает сеть через построение популяции/роя. Каждая нейронная сеть здесь представлена как вектор нагрузки и скорректирована по отношению к позиции глобальной лучшей частицы и ее собственной лучшей позиции.
Эта функция приспособления просчитывается как сумма квадратов ошибок реконструированной нейронной сети после завершения одного прямого прохождения. Выгоду получаем на оптимизации скорости обновления весов связей. Если весы будут регулироваться слишком быстро, сумма квадратов ошибок стагнирует, обучение не происходит.
Генетический алгоритм строит популяцию вектора, представляющего нейронную сеть. Далее с ней проводятся три последовательные операции для улучшения работы сети:
- Выборка: после каждого прямого прохождения подсчитывается сумма квадратов ошибок, популяция нейронной сети ранжируется. Верхний процент популяции выбирается для выживания и используется для кроссовера.
- Кроссовер: верхний x% генов популяции соревнуется между собой, получаем некое новое потомство, каждое потомство представляет, по сути, новую нейронную сеть.
- Мутация: этот оператор требует поддержки генетического разнообразия в популяции, небольшой процент ее отбирается для прохождения мутации, то есть некоторые весы сети будут регулироваться случайно.
6. Нейронным сетям не всегда нужен большой объем данных
Нейронные сети могут использовать три основных обучающих стратегии: контролируемое обучение, неконтролируемое и усиленное обучение. Для первой, нужны, по крайней мере, два обучающих сета данных. Один из них будет состоять из входных с ожидаемыми выходными сигналами, второй с входными без ожидаемых выходных. Оба должны включать маркированные данные, то есть паттерны с изначально неизвестным предназначением.
Неконтролируемая стратегия обычно используется для выявления скрытых структур в немаркированных данных (например, скрытых цепей Маркова). Принцип работы тот же, что и у кластерных алгоритмов. Усиленное обучение основано на простом допущении о наличие выигрышных сетей и помещении их в плохие условия. Два последних варианта не подразумевают использование маркированных данных, поэтому правильный выходной сигнал здесь неизвестен.
Неконтролируемое обучение
Одна из самых популярных архитектур для такого типа сети – самоорганизующаяся карта. По сути, это техника масштабирования в нескольких измерениях, которая конструирует приближение функции плотности вероятности какого-либо основного цикла данных. Z – сохраняет топологическую структуру сета данных, картируя векторы входных сигналов – zi. Она взвешивает векторы — vj, в будущей карте V. Сохранение топологической структуры означает, что, если два вектора стоят близко друг к другу в Z, нейроны, к которым они относятся, также будут расположены в V. Более подробно можно почитать здесь.
Усиленное обучение
Эта стратегия состоит из трех компонентов: установки на то, как нейронная сеть будет принимать решения, используя технические и фундаментальные индикаторы, функции достижения цели, которая отделяет зерна от плевел, и функции значения, нацеленной на перспективу.
7. Нейронную сеть нельзя обучить на любых данных
Одна из главных проблем, почему нейронная сеть может не работать, заключается в том, что нередко данные плохо готовят перед загрузкой в систему. Нормализация, удаление избыточной информации, резко отклоняющихся значений должны проводиться перед началом работы с сетью, чтобы улучшить ее производственные возможности.
Мы знаем, что у нас есть слои перцептронов, соединенных по весу. Каждый перцептрон содержит функцию активации, который, в свою очередь, разделены по рангу. Входные сигналы должны быть масштабированы, исходя из этого ранга, чтобы сеть могла различать входные паттерны. Это предпосылки для нормализации данных.
Резко выделяющиеся значения или намного больше или намного меньше большинства других значений в наборе данных для сета. Такие вещи могут вызвать проблемы в применении статистических методов – регрессии и подгонки кривой. Потому что система постарается приспособить эти значения, производительность ухудшится. Выявить такие значения самостоятельно может быть проблематично. Здесь можно посмотреть инструкцию по техникам работы с резко отклоняющимися значениями.
Внесение двух или более независимых переменных, которые близко коррелируют друг с другом также может вызвать снижение способности к обучению. Удаление избыточных переменных, ко всему прочему, ускоряет время обучения. Для удаления избыточных соединений и перцептронов можно использовать адаптивные нейронные сети.
8. Нейронные сети иногда требуется обучать заново
Даже если вы настроили должным образом нейронную сеть, и она торгует успешно в выборке и за ее пределами, еще не значит, что через некоторое время она не перестанет работать. Дело не в ней, дело в том, как ведет себя финансовый рынок. Финансовые рынки – комплексные адаптивные системы. То, что работает сегодня, может не работать завтра. Эту их характеристику называют нестационарностью или динамической оптимизацией. Нейронные сети пока не умеют с этим справляться.
Динамическая среда финансовых рынков очень сложная штука для моделирования нейронной сетью. Есть два выхода из ситуации: время от времени переобучать сеть или использовать динамическую нейронную сеть. Она призвана отслеживать изменения в среде по времени и приспосабливать их к архитектуре и нагрузке системы. Для решения динамических проблем можно использовать многосторонние мета-эвристические алгоритмы оптимизации. Они будут отслеживать изменения к локальному опыту по времени. Один из вариантов – оптимизация множественного роя, производная от метода роя частиц. Генетические алгоритмы с улучшенной диверсификацией и памятью также могут быть полезны в динамичной среде.
9. Нейронная сеть – это не черный ящик
Сама по себе нейронная сеть – это «черный ящик». Это создает определенные проблемы для людей, которые работают или планируют с ней работать. Например, фондовые управляющие не понимают, как система принимает решения по финансовым операциям. Отсюда получается, что нельзя рассчитать риск трейдинговой стратегии, которой обучилась сеть. Опять же банки, использующие нейронную сеть для просчетов кредитных рисков, не могут верифицировать ее позиции по кредитному рейтингу для тех или иных клиентов. Для этих целей были придуманы алгоритмы извлечения правил работы сети. Знания могут быть вытащены из сети в виде математических формул, символической логики, нечеткой логики, дерева решений.

Математические правила: некоторые алгоритмы позволяют извлекать множественные строки линейной регрессии. Проблема в том, что зачастую они понятны только в контексте работы «черного ящика».
Пропозициональная логика: раздел математической логики, который имеет дело с дискретными значениями переменных. Эти переменные A и B чаще всего имеют значения «верно» — «неверно», но также могут иметь значения дискретного уровня – «покупать, «удерживать», «продавать».
К ним применимы логические операции: OR, AND и XOR. Результаты этих операция называются предикатами, количественные значения которых также можно рассчитать. Между предикатами и пропозициональной логикой есть различие. Если у нас простая нейронная сеть с ценой (P), простым скользящим средним (SMA), экспоненциальным скользящим средним (EMA) в качестве входных сигналов, и мы хотим извлечь тренд стратегии в пропозициональной логике, мы действуем по следующим правилам:
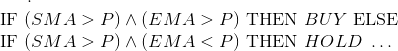
Нечеткая логика (fuzzy logic) – это то место, где встречается вероятность и пропозициональная логика. Последняя имеет дело с абсолютами – «купить», «продать», «верно», «неверно», 0 или 1. Трейдер никак не может подтвердить подлинность этих результатов. Нечеткая логика преодолевает это ограничение, вводя функцию членства, обозначающую принадлежность переменной к определенной области, домену. Например, компания (GOOG) имеет значение 0,7 в домене BUY и 0,3 в домене SELL. Комбинация такой логики и нейронной сети называется нейро-нечеткая система.
Дерево решений показывает, как принимаются решения при загрузке определенной информации. В этой статье можно почитать, как построить анализ безопасности дерева решения, используя генетическое программирование.
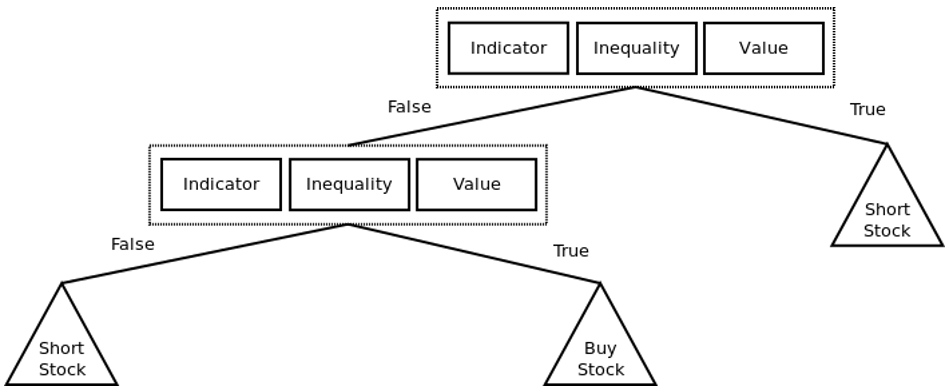
Пример простой стратегии онлайн-трейдинга, представленной в виде дерева решений. Треугольники представляют узлы решений (например, BUY, HOLD или SELL для покупки, удержания или продажи акций). Каждый элемент представляет собой пару
<indicator, inequality,="" value="">. Например, <sma,>, 25> or <ema, <="," 30="">.
10. Нейронную сеть создать и применить нетрудно
Если говорить о практике, создать нейронную сеть с нуля довольно проблематично. К счастью, сейчас существуют сотни пакетов с открытым доступом, которые делают работу с нейронными сетями немного проще. Ниже приведен список таких пакетов, которые можно пользовать в количественном анализе в финансовой сфере. Список далеко не полный, инструменты даны в алфавитном порядке.
Caffe
Сайт - http://caffe.berkeleyvision.org/
Репозиторий на GitHub - https://github.com/BVLC/caffe
Encog
Сайт - http://www.heatonresearch.com/encog/
Репозиторий на GitHub - https://github.com/encog
H2O
Сайт - http://h2o.ai/
Репозиторий на GitHub - https://github.com/h2oai
Google TensorFlow
Сайт - http://www.tensorflow.org/
Репозиторий на GitHub - https://github.com/tensorflow/tensorflow
Microsoft Distributed Machine Learning Tookit
Сайт - http://www.dmtk.io/
Репозиторий на GitHub - https://github.com/Microsoft/DMTK
Microsoft Azure Machine Learning
Сайт - https://azure.microsoft.com/en-us/services/machine-learning
Репозиторий на GitHub — github.com/Azure?utf8=%E2%9C%93&query=MachineLearning
MXNet
Сайт - http://mxnet.readthedocs.org/en/latest/
Репозиторий на GitHub - https://github.com/dmlc/mxnet
Neon
Сайт - http://neon.nervanasys.com/docs/latest/index.html
Репозиторий на GitHub - https://github.com/nervanasystems/neon
Theano
Сайт - http://deeplearning.net/software/theano/
Репозиторий на GitHub - https://github.com/Theano/Theano
Torch
Сайт - http://torch.ch/
Репозиторий на GitHub - https://github.com/torch/torch7
SciKit Learn
Сайт - http://scikit-learn.org/stable/
Репозиторий на GitHub - https://github.com/scikit-learn/scikit-learn
Заключение
Нейронные сети – это класс мощных алгоритмов машинного обучения. В их основе лежат статистические методы анализа. Вот уже много лет их с успехом применяют к разработке стратегий трейдинга и финансовых моделей. Несмотря на это, у нейронных сетей не очень хорошая репутация, основанная на неудачах практического применения. В большинстве случаев причины неудач лежат в неадекватных конструкторских решениях и общем непонимании того, как они работают. В этой статье автор попытался артикулировать лишь некоторые из самых распространенных заблуждений в надежде, что кому-нибудь эта информация пригодится в реальной практике.
Другие материалы по теме от ITinvest:
- Аналитические материалы о ситуации на финансовых рынках от экспертов ITinvest
- Можно ли создать алгоритм для торговли на бирже с помощью анализа тональности сообщений в интернете
- Как определить наилучшее время для сделки на фондовом рынке: Алгоритмы следования тренду
- ИБ-стартап Palantir поможет инвестбанку Credit Suisse создать систему для выявления недобросовестных трейдеров
- Эксперимент: Использование Google Trends для прогнозирования обвалов фондового рынка
- Эксперимент: создание алгоритма для прогнозирования поведения фондовых индексов
Комментарии (2)

sash_sokolov
30.05.2016 15:51Цитата:
Опять же банки, использующие нейронную сеть… не могут верифицировать ее позиции по кредитному рейтингу для тех или иных клиентов. Для этих целей были придуманы алгоритмы извлечения правил работы сети. Знания могут быть вытащены из сети в виде математических формул, символической логики, нечеткой логики, дерева решений.
Есть и вправду много работ, посвященных вытаскиванию правил, но это полный кошмар и на практике этим занимаются неохотно. А вот насчет перечисленных в последнем предложении методов — так есть эти алгоритмы, обучающиеся! Обучаете сразу их (математические формулы даст GMDH алгоритм (в т.ч. и его вариант нейронной сети), нечеткая логика — ANFIS сети, главный плюс еще и в том, что можно вносить априорные знания в конструкцию сети, а деревья решений… соб-но есть такой класс алгоритмов (главный плюс — отлично параллеляться). И вдогонку авторам — почитайте про вейвлет нейронные сети (в варианте. предложенном Q.Zhang и A. Benveniste еще в 1992-м) — при недостатке данных и сильной их загрязенности лучший инструмент для работы с вр. рядами.


valemak
Некоторая смысловая путаница с заголовком публикации и подзаголовками в самой статье. Названия всех 10-ти пунктов являются верными суждениями о нейронных сетях, но в названии статьи говорится о 10-ти заблуждениях. Если уж действительно хочется написать в духе: «вот миф, а мы его опровергаем», то подзаголовки уместнее бы так сформулировать:
1. Нейронная сеть – это модель человеческого мозга
2. Нейронная сеть – упрощенная форма статистики
3. Нейронная сеть может быть исполнена только в одной архитектуре
и т.д. и т.п.