Человек издревле пытался понять устройство окружающего его мира и найти свое место в нем. Упорство и изобретательность его разума в течение тысяч лет приближали человека к объективному пониманию мира вопреки закрепленному культурой субъективному (не редко ложному) восприятию. Одной из первых задач к достижению этих целей является определение масштабов окружающего нас мира.

В данном обзоре я ознакомлю вас с историей постижения человеком масштабов мироздания с эпохи изобретательных греков и до современной эры высоких технологий. Вы узнаете, почему «плоская Земля на трех китах» вызывала смех еще у древних римлян, как современники короля-солнце определили межпланетные расстояния и каким образом космические катаклизмы помогают постигать вселенские масштабы.

Масштабы греческого гения

Античные греческие мыслители одними из первых пошли на интеллектуальный штурм тайны масштабов нашего мира. Особняком среди них стоит один из величайших античных астрономов Аристарх Самосский (4-3 век до н.э.), решивший рассчитать относительные расстояния между Землей, Солнцем и Луной, используя довольно развитый геометрический аппарат своего времени.

Аристарх правильно предполагал, что Луна имеет форму сферы и получает свет от Солнца. Следовательно, в фазе половины месяца лучи Солнца падали на Луну точно перпендикулярно лучу зрения земного наблюдателя. Таким образом, измеряя угловое расстояние между центрами Луны и Солнца на небосводе Земли, можно было рассчитать относительные расстояния, используя принципы геометрии треугольника. Измеренный угол составил 87, на основе которого Аристарх рассчитал, что Солнце находится от Земли в 19 раз дальше, чем Луна. Зная, что угловые размеры Солнца и Луны на небе совпадают (об этом свидетельствовали солнечные затмения), Аристарх решил, что Солнце в те же 20 раз больше Луны.

Такая 20 кратная ошибка относительно реального положения дел объясняется тем, что без точных астрономических инструментов крайне трудно определить точный момент квадратуры (половины месяца). Однако прогресс был на лицо, учитывая то, что многие астрономы его времени считали, будто Солнце может иметь размеры с большой греческий полис.

Тангенс угла 87° как уже показано был равен 19,08, тангенс угла 89° чуть больше 57, ну а тангенс истинной квадратуры ~89,85° уже близок к 400. т.е. такой метод очень требователен к точности определения угла альфа


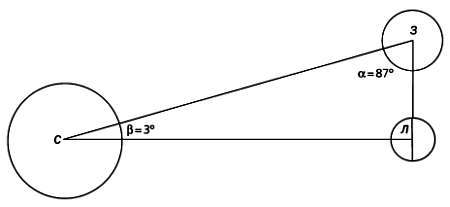
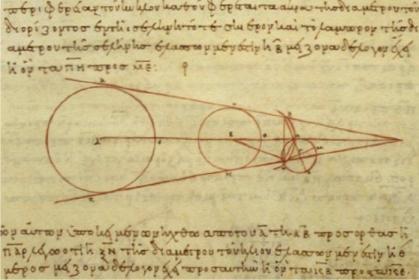
Ученый пошел дальше, решив установить относительные размеры Луны и Земли используя уже лунные затмения. Очередной раз, правильно решив, что Луна затмевается тенью Земли, а угловой размер тени на орбите Луны вдвое больше последней, Аристарх заключает, что радиус Земли (принятый за условную единицу) больше лунного в 3 раза (современная оценка 3,6). В таком случае получалось, что радиус Солнца больше земного более чем в 6 раз (современная оценка 109 раз).

Древнегреческая схема вычислений расстояния до Луны и ее размеров


Видимо огромные размеры Солнца впервые в истории навели Аристарха на мысль о том, что именно Земля вращается вокруг светила, а не наоборот, как тогда принято было считать. На возражения о том, почему в таком случае сфера звезд не меняет своего положения относительно небесной сферы из-за движения Земли (отсутствие параллакса, ученый предположил, что расстояние до звезд слишком велико относительно радиуса земной орбиты, и потому параллакс не виден невооруженному глазу. Однако идея не получила распространения в античном мире, предположительно по религиозным причинам (религиозная цензура в научном мире вовсе не изобретение христианского средневековья).

Паралла?кс (греч. ????????, от ?????????, «смена, чередование») — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя. Зная расстояние между точками наблюдения (база) и угол смещения, можно определить расстояние до объекта. Параллакс используется в геодезии и астрономии для измерения расстояния до удалённых объектов. На явлении параллакса основано бинокулярное зрение. (Wiki)

Через столетие, другой греческий астроном Гиппарх Никейский, более точно определив угловые размеры земной тени и Луны определил, что Земля больше Луны в 3,5 раз. Гиппарх уже знал, что любое тело наблюдается под угловым размером в 1 минуту на расстоянии в 3483 больше его реальных размеров. Таким образом, взяв за единицу радиус Земли и зная угловые размеры Луны, Гиппарх определил расстояние до Луны как 60 радиусов нашей планеты (почти как и сегодня). Расчеты на основе трудов Аристарха давали результат в 80 радиусов Земли.

Однако пытливому греческому уму было недостаточно отсчитывать расстояния в радиусах Земли, встал вопрос и об определении истинных размеров нашей планеты. Сделано это было человеком, жившим в одно время с Аристархом – александрийским ученым Эратосфеном Киренским.

Эратосфен полагал, что подобно Солнцу, Луне и небесной сфере Земля имеет форму шара (как принято было считать в философии Аристотеля), и точно так же как и небесная сфера которую пересекают меридианы, последние мысленно могут пересекать и поверхность Земли. Таким образом, рассчитав окружность земного меридиана, можно было получить величину земного радиуса. Мысленный меридиан Эратосфен расположил на линии соединяющей египетские города Александрию и более южную Сиену. Далее, полагая, что оба города почти равноудалены от Солнца, Эратосфен, в каждом из них, определил высоту Солнца над горизонтом по длине тени солнечных часов ровно в полдень (дни летнего солнцестояния). Зная расстояние между широтами городов и угол падения солнечных лучей в них, можно было легко определить всю длину меридиана.



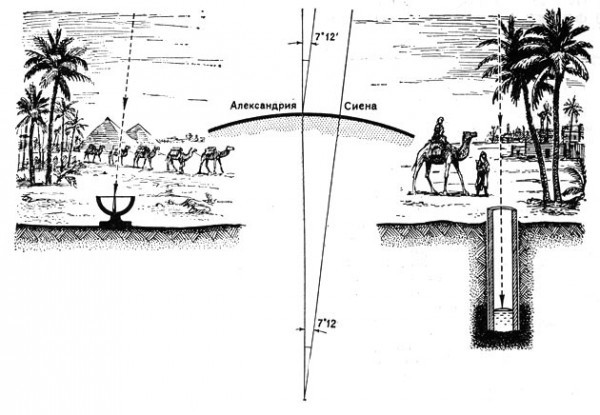
Радиус Земли был определен Эратосфеном в 250 000 стадий. К сожалению, мы не знаем, какими именно стадиями пользовался ученый, египетскими или греческими. В первом случае погрешность относительно истинных размеров составляет 1,5%, но даже если радиус был получен в греческих стадиях, то результат все равно впечатляющий — 7080 км (в реальности 6378км, погрешность около 10%).

Предсказуемый хаос

Синтезом античного представления о строении Вселенной стал классический труд «Математическое собрание в 13 книгах», древнегреческого астронома Клавдия Птолемея (2 век н.э.). Геоцентрическая система Птолемея опиралась не только на философию и авторитет Аристотеля, но и солидный математический аппарат, а так же наблюдения многих авторитетных античных астрономов (в частности Гиппарха).

Еще в глубокой древности люди заметили, что планеты, Луна и Солнце движутся по определенному «коридору» на небесной сфере, в районе 13 созвездий (12 из которых в результате стали Зодиакальными). Годичный путь Солнца по этому коридору был назван эклиптикой. При этом планеты, в отличие от Луны и Солнца, двигаются не равномерно, описывая круги (попятное движение), заметное на видео ниже.



Система Птолемея явилась сложной математической моделью описывавшей данное движение и позволявшее рассчитывать эфемериды (положения планет) на будущее с рекордной точностью в 10 угл. мин. (треть полного диска Луны). На основе своей модели ученый полагал, что планеты совершали круговые движения по эпициклам, центр которых обращался по орбите (деференту) вокруг центра. Причем центр находился на некотором удалении от Земли. Хотя такая система и не выглядела реалистично, но позволяла парировать погрешности вычисления положений небесных тел.



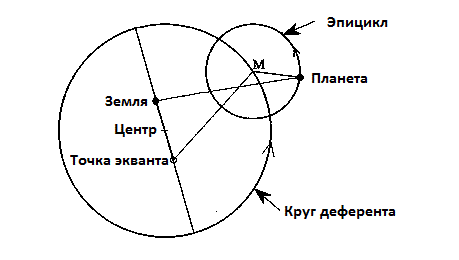
Еще за столетия до работ Птолемея, греки прекрасно разбирались в динамике небесных тел и даже создавали своего рода примитивные компьютеры для расчета эфемерид и затмений, как например антикитерский механизм.

Реконструкция работы антикитерского «компьютера» с помощью конструктора Lego


Геоцентризм оставался основой космологии до конца 17 века, уточняясь и усложняясь в течение всех средних веков благодаря работам интеллектуалов христианского и мусульманского мира. Работы Птолемея активно использовались и для морской навигации в начале эпохи Великих географических открытий.

В «Новый свет» по пути заблуждения

В средние века, как и в позднюю античность, доминировала версия о шарообразности Земли, разделяемая, в том числе, большинством философов и теологов. Основные расхождения вызывал вопрос о размерах нашей планеты.

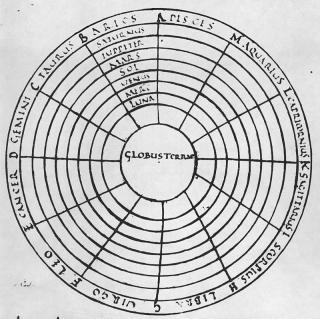
Globus Terrae («Земной шар») на геоцентрической схеме раннего средневековья


Итальянский мореплаватель Христофор Колумб, поступивший на службу испанской короне, в 1492 году отплыл на запад, полагая, что Земля вдвое меньше оценок Эратосфена, и имеет грушеобразную форму. Открытие «Индии» добавило вес противникам теории Эратосфена, но ненадолго. Экспедиции другого итальянца и знакомого Колумба – Америго Веспуччи убедят европейцев в том, что Колумб открыл «Новый свет», а не путь в Азию. Впоследствии за новой частью света закрепится имя известного исследователя – Америка.

Америго Веспуччи на фоне составленной им карты южной части нового света


Модель Земли Эратосфена получит опытное подтверждение через 30 лет после первого плавания Колумба, в результате первой в истории кругосветной экспедиции испанской эскадры под руководством португальца Фернана Магеллана.

Эпоха Великих астрономических открытий

После опытного осознания масштабов своей планеты, внимание человеческого разума сконцентрировалось уже на постижении масштабов вселенной. В 1543 году, польский астроном Николай Коперник завершил свой 40 летний труд «О вращении небесных сфер», с которого начался закат птолемеевской системы мира и становление системы гелиоцентрической. Парадоксально, но на фоне расцвета Святой Инквизиции, церковь на первых порах положительно отнеслась к труду Коперника. Его система была значительно проще птолемеевской, сильно упрощая расчеты положения небесных тел. Помогло то, что один из друзей Коперника, вопреки его воле, добавил в книгу заметку о том, что гелиоцентрическая система является сугубо математической абстракцией, не имеющей отношения к действительности.

«Коперник. Беседа с Богом» (худ. Матейко), справа фрагмент его труда со схемой гелиоцентрической системы мира


Коперник верно интерпретировал попятные движения планет тем, что Земля, двигаясь по своей орбите вокруг Солнца, сначала догоняла внешнюю планету (она постепенно замедляла движение на небесной сфере), и затем после противостояния обгоняла ее (планета останавливалась и пятилась в обратную сторону). По углам попятных движений можно было определять относительные расстояния планет от Солнца близкие современным (Птолемей, как и Аристарх, считал, что Солнце удалено на 20 радиусов лунной орбиты). Впервые Коперник определил и порядок удаления планет от центрального светила, объяснив «нежелание» Венеры и Меркурия удалятся от Солнца более чем на 45° тем что они обращаются вокруг Солнца внутри Земной орбиты.

Однако гелиоцентризм в то время имел и серьезные недостатки. Так астрономы сетовали на то, что модель по точности расчетов не превосходила птолемеевскую. Коперник полагал, что орбиты планет были идеально круглыми (имели эксцентриситет равный нулю), что со временем приводило к существенным погрешностям измерений. Как и Аристарх, Коперник столкнулся с проблемой отсутствия параллакса звезд.

Учитывая эти недостатки системы Коперника, знаменитый датский астроном (точнее астролог) Тихо Браге, живший во второй половине 16 века, предложил свою версию планетной системы. В основном она в точности повторяла гелиоцентризм, все планеты вращались вокруг Солнца, однако последнее вращалось вокруг Земли, помещенной в центр мироздания. Так Браге объяснял отсутствие параллакса, отбрасывал по критерию «лишних сущностей» огромную пустоту между планетами и сферой звезд, а так же удовлетворял принципам схоластики (средневековая христианская философия с сильной примесью аристотелизма).

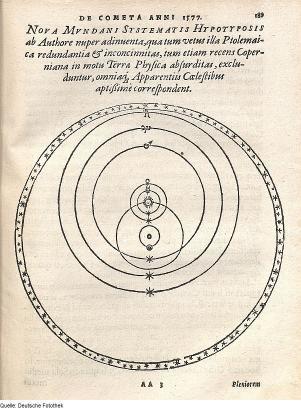
Гео-гелиоцентрическая система Брагэ


Тихо Браге накопил огромный научный материал, составив новые звездные каталоги рекордной точности, и впервые в истории накопил солидную статистическую базу по наблюдению за движением планет, в частности Марса. За эту методичность Браге впоследствии назвали первым в истории ученым в современном понимании этого слова. Парадоксальность ситуации в том, что Браге считал себя астрологом (как и Птолемей с Коперником), и открыто говорил, что если бы не астрология, то в астрономии не было бы никакого смысла.

Марс, «яблоко» всемирного тяготения

Труд Тихо Браге по иронии судьбы оказал огромную услугу гелиоцентризму. Основываясь на его наблюдениях за Марсом, знаменитый немецкий астроном, астролог и друг Браге, Иоганн Кеплер сформулировал первые законы движения планет. Главные принципы его работ постулировали, что скорость движения планеты падает с удалением от Солнца, а орбиты планет не являются круговыми (как полагал Коперник), имея форму эллипсиса в одном из фокусов которого находится Солнце (а не в центре). Это позволило значительно усовершенствовать систему Коперника, удалив из нее такие рудименты системы Птолемея, как эпициклы (оставленные для парирования неравномерного движения по орбите). Уравнение Кеплера позволяло рассчитать скорость планеты в любой точке орбиты и определить ее период обращения. Однако Кеплер сохранял веру в сферу звезд, аргументируя отсутствие бесконечной вселенной заполненной звездами тем, что позже Эдмунд Галлей назовет фотометрическим парадоксом.

Дудл в честь 442 летия со дня рождения Иогана Кеплера. Ученый изображен в центре орбиты Земли обращающейся по эллиптической орбите в одном из фокусов которой находится Солнце. Можно заметить что скорость планеты падает с увеличением расстояния от Солнца. Названный в честь ученого космический аппарат «Кеплер» в 2009-2013гг. открыл более 1000 экзопланет


Несмотря на бесперспективную точность системы Кеплера, в 1616 году католическая церковь на два столетия запретила своей пастве считать гелиоцентризм чем – то большим, нежели абстрактная математическая модель. «Богомерзким» гелиоцентризм считали и авторитеты протестантской церкви. Следует помнить, что бурный расцвет наук в Европе первой половины 17 века, сочетался с разрушительными религиозными войнами и громким религиозным судом над видным ученым.

Современник Кеплера, итальянский ученый Галилео Галилей, впервые направив в небо телескоп (1609г), опроверг космологию Аристотеля, показав что «небесные сферы» вовсе не идеальны, на Солнце были видны пятна, а на Луне есть кратеры и горные цепи. Вдобавок он обнаружил у Юпитера 4 луны (1610г), что эмпирические опровергало тезис Аристотеля о том, что все небесные тела вращаются вокруг Земли. За поддержку гелиоцентризма, Галилей предстанет перед судом инквизиции в 1633 году.

Галилей перед Инквизицией (худ. Кристиано Банти)


Однако это не остановит научную мысль. Благодаря законам Кеплера и изобретенному телескопу, гелиоцентрическая система сделает огромные успехи в течение всего 17 века. Были получены точные относительные положения планетных орбит в солнечной системе, за единицу расстояния принимался радиус земной орбиты (астрономическая единица). Точность небесной механики Кеплера была такова, что определив абсолютное расстояние между любыми двумя телами солнечной системы, можно было определить все остальные расстояния и осознать абсолютные размеры солнечной системы (тогда наиболее удаленной планетой был Сатурн).

В этом снова помогла солидная статистика наблюдений за Марсом. В 1672 году, во время правления «короля-солнце» (Людовик 14го), французские астрономы Кассини и Рише сумели определить параллакс Марса на фоне далеких звезд, впервые вычислив абсолютное расстояние до него. Благодаря этому Кассини с довольно высокой точностью определил значение астрономической единицы – 146 млн. км (современное значение – 149 млн. км). Через 3 года, в 1675 году, датский астроном Ремер работавший вместе с Кассини в Париже, обнаружил запаздывание в расчетах по движению спутников Юпитера и определил конечность скорости света с погрешностью в 30% (1676г).

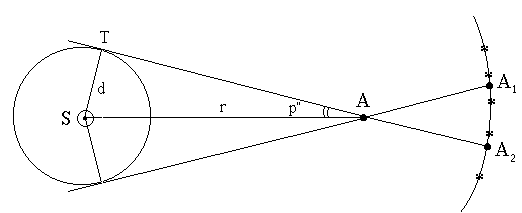
Схема параллакса Марса. Две точки обзора были удалены на поверхности Земли (Кассини в Париже и Рише в Кайенне, Южная Америка). В один момент времени положение Марса относительно звезд в этих точках отличалось, что позволило ученым вычислить расстояние до планеты


В 1687 году, опираясь на небесную механику Кеплера, гений Исаака Ньютона сформулирует законы всемирного тяготения, еще больше увеличившие точность небесной механики и описывавшие гравитационные взаимодействия в солнечной системе. Таким образом, астрономические наблюдения так же привели к революции в прикладных науках. Астрономическая единица будет уточняться вплоть до эпохи радиолокационных измерений в 20 веке. В 18 и 19 века для этого будут использовать параллакс Венеры при ее прохождении по диску Солнца. Во время одного из таких прохождений Ломоносов откроет атмосферу планеты в 1761 году.

В 1727 году, английский астроном Брэдли, в поисках параллакса звезд действительно обнаруживает изменение их положения на небесной сфере с годичным движением Земли. Однако это изменение не было похоже на параллакс, и Брэдли верно интерпретировал явление аберрацией – изменение направления скорости Земли относительно света звезды. Так Брэдли подтвердил конечность скорости света (на уровне 300 000 км/с) и эмпирические доказал орбитальное движение Земли вокруг Солнца.

Аналогичная программа поиска звездного параллакса в 1781 году приведет английского астронома Гершеля к открытию планеты Уран. Настоящим же триумфом небесной механики станет открытие Нептуна «на кончике пера» в 1846 году английским астрономом Адамсом и его французским коллегой Леверье.

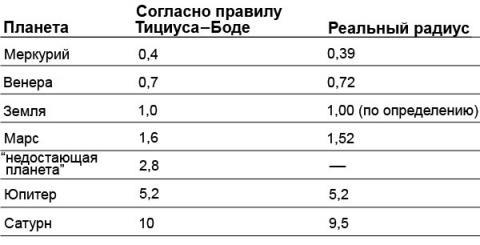
Параметры орбиты Урана косвенно подтверждали популярное тогда среди ученых правило Тициуса-Боде, простой арифметической закономерности удаления планет от Солнца. Так поиски недостающей планеты между орбитами Марса и Юпитера привели в начале 19 века к открытию пояса астероидов. Однако открытие Нептуна опровергло этот математический курьез, да и суммарная масса астероидов «разрушенного Фаэтона» не превышала и 5 % от массы Луны


Целостная картина механики планет солнечной системы будет завершена лишь в 20 веке с помощью теории относительности Эйнштейна, успешно объяснившей аномалии орбиты Меркурия. Однако уже в 18 веке началась «охота на звездный параллакс», попытки человеческого разума пробить брешь «сферы звезд» и выйти на межзвездные просторы.

Во второй части хроники постижения масштабов нашего мира, я поведаю вам воистину детективную историю об определении человеком межзвездных расстояний и дальше – вплоть до окраин видимой Вселенной.