Суффиксное дерево – мощная структура, позволяющая неожиданно эффективно решать мириады сложных поисковых задач на неструктурированных массивах данных. К сожалению, известные алгоритмы построения суффиксного дерева (главным образом алгоритм, предложенный Эско Укконеном (Esko Ukkonen)) достаточно сложны для понимания и трудоёмки в реализации. Лишь относительно недавно, в 2011 году, стараниями Дэни Бреслауэра (Dany Breslauer) и Джузеппе Италиано (Giuseppe Italiano) был придуман сравнительно несложный метод построения, который фактически является упрощённым вариантом алгоритма Питера Вейнера (Peter Weiner) – человека, придумавшего суффиксные деревья в 1973 году. Если вы не знаете, что такое суффиксное дерево или всегда его боялись, то это ваш шанс изучить его и заодно овладеть относительно простым способом построения.

Прежде чем переходить к описанию суффиксного дерева, определимся с терминологией. Входные данные для алгоритма – это строка s, состоящая из n символов s[0], s[1], …, s[n-1]. Каждый символ – это байт. Хотя, конечно, всё описываемое здесь будет работать и для любых других последовательностей: битов, двухбайтовых символов юникода, двухбитовых символов последовательностей ДНК и так далее. Дополнительно будем полагать, что s[n-1] равен символу 0, который нигде более в s не встречается. Это последнее ограничение служит лишь для упрощения повествования и от него, на самом деле, достаточно просто избавиться. Строки вида s[i..j] = s[i]s[i+1]…s[j], где i и j – некоторые целые числа, называются, как обычно, подстроками. Подстроки вида s[i..n-1], где i – некоторое целое, называются суффиксами.

Итак, главный герой. Суффиксное дерево для строки s – это минимальное по числу вершин дерево, каждое ребро которого помечено непустой подстрокой s таким образом, что каждый суффикс s[i..n-1] может быть прочитан на пути из корня до какого-нибудь листа и, наоборот, каждая строка, прочитанная на пути из корня до какого-нибудь листа, является суффиксом s. Проще всего разобраться с этим определением на пример (не обращайте внимания, пока что, на pos, len и to):


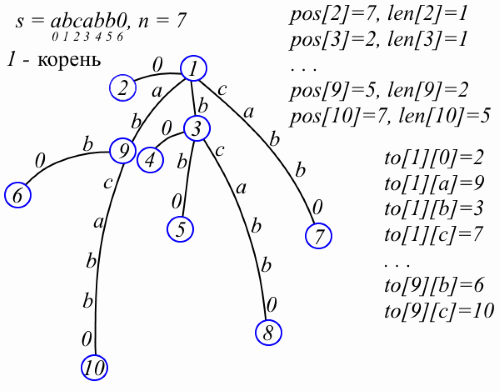
Поскольку s[n-1] — это особый символ, в суффиксном дереве ровно n листьев, а значит O(n) вершин. Вершины мы будем нумеровать целыми числами. Метка на ребре из вершины v в отца v хранится в виде пары чисел: длина метки len[v] и позиция pos[v] сразу после этой метки в s, т.е. если метка – это строка t, то t = s[pos[v]-len[v]..pos[v]-1]. Пусть некоторая вершина v имеет k детей и t₁, t₂, …, t_k – это метки на рёбрах от v к детям. Заметьте, что первые символы строк t₁, t₂, …, t_k попарно различны, а значит ссылки на детей v можно хранить в мапе to[v], отображающем первый символ метки в соответствующего отпрыска. Я буду избегать объектно-ориентированного подхода в описании структур, чтобы сделать код короче и чтобы вы подумали «ух ты, какой компактный код». Итак, суффиксное дерево представлено следующим образом (теперь можно обратить внимание на pos, len, и to на рисунке выше):

int sz; //количество вершин в дереве
int pos[0..sz-1], len[0..sz-1], par[0..sz-1]; //par[v] – отец вершины v
std::map<char, int> to[0..sz-1]; //to[v] – ссылки на детей вершины v

Первое важное свойство – суффиксное дерево занимает O(n) памяти.

Строку, написанную на пути от корня до вершины v, будем обозначать str(v); str(v) используется только в рассуждениях и нигде явно не хранится.

Примеры использования суффиксного дерева

Чтобы освоиться с суффиксным деревом и одновременно понять, как его использовать, рассмотрим несколько примеров.

Поиск подстроки в s

Возможно, самое первое что приходит в голову – это использовать суффиксное дерево для поиска подстрок. Довольно просто заметить, что строка u является подстрокой строки s тогда и только тогда, когда u можно прочитаться из корня суффиксного дерева (т.к. u = s[i..j] для некоторых i и j и поэтому суффикс s[i..n-1] начинается с u).

Количество различных подстрок в строке s

Теми же рассуждениями можно установить, что каждая подстрока s соответствует некоторой позиции на метке какого-то ребра суффиксного дерева. Значит число различных подстрок – это число таких позиций и оно равно сумме len[v] по всем вершинам v кроме корня.

Сжатие данных LZ77

Пример посложнее. Идея сжатия LZ77 (гуглите Lempel, Ziv) проста и может быть описано таким псевдокодом:

for (int i = 0; i < n; i = j+1) //сжимаем строку s[0..n-1]
	if (символ s[i] не встречался ещё в s[0..i-1]) {
		j = i, записать в выходной файл символ s[i]; //точный формат записи зависит от реализации
	} else {
		j = max{j для которого найдётся d < i такое, что s[i..j] = s[d..d+j-i]};
		d = позиция 0,1,…,i-1 такая, что s[d..d+j-i] = s[i..j];
		записать в выходной файл пару чисел (j-i+1, i-d) //точный формат записи зависит от реализации
	}
}

Например, строка “aababababaaab” будет закодирована как “a(1,1)b(7,2)(3,10)” (обратите внимание на “перекрытие” строк abababa). Конечно, детали реализации могут сильно отличаться, но основная идея используется во многих алгоритмах сжатия. С помощью суффиксного дерева можно сжать s подобным образом за O(n). Для этого мы дополняем каждую вершину v нашего дерева полем start[v] таким, что start[v] равно наименьшему p при котором s[p..p+|str(v)|-1] = str(v), где |str(v)| – это длина str(v). Ясно, что для листьев это значение легко вычисляется. Для остальных вершин поле start вычисляется одним обходом дерева в глубину, т.к. start[v] = min{start[v₁], start[v₂], …, start[v_k]}, где v₁, v₂, …, v_k – дети v. Теперь, чтобы вычислить очередное значение j в нашем алгоритме сжатия, достаточно читать строку s[i..n-1] из корня до тех пор, пока текущая вершина v в дереве имеет start[v] < i; d можно выбрать равным последнему такому значению start[v].

Построение суффиксного дерева

Заранее предупрежу, что несмотря на то, что упрощённый алгоритм Вейнера проще, чем алгоритм Укконена и классический алгоритм Вейнера, он, тем не менее, по-прежнему является нетривиальным алгоритмом, и чтобы понять его, необходимо приложить некоторые усилия.

Общий план. Префиксные ссылки

Алгоритм стартует с пустого дерева и последовательно добавляет суффиксы s[n-1..n-1], s[n-2..n-1], …, s[0..n-1]:

for (int i = n-1; i >= 0; i--)
	extend(i); //добавить в дерево суффикс s[i..n-1]

Таким образом на k-й итерации цикла мы имеем суффиксное дерево для строки s[n-k+1..n-1] и добавляем в дерево суффикс s[n-k..n-1]. Ясно, что добавление нового самого длинного суффикса требует вставки одного нового листа и, возможно, одной новой вершины, «разбивающей» старое ребро. Основная проблема – найти позицию в дереве, где будет присоединён новый лист. Для решения этой проблемы суффиксное дерево дополняется префиксными ссылками.

С каждой вершиной v мы ассоциируем префиксные ссылки link[v] – мап, отображающий символы в номера вершин следующим образом: для символа a link[v][a] определено тогда и только тогда, когда в дереве существует вершина w такая, что str(w) = a str(v) и в этом случае link[v][a] = w. (Если вы были знакомы с классическим алгоритмом Вейнера, то заметили, что наши префиксные ссылки соответствуют «явным» классическим префиксным ссылкам, а «неявные», оказывается, вообще не требуются; если же вы были знакомы с алгоритмом Укконена, то могли заметить, что префиксные ссылки – это обращённые «суффиксные ссылки».) На рисунке префиксные ссылки обозначены красным, а в прямоугольниках написаны символы, соответствующие ссылкам (смысл фиктивной вершины 0 смотрите ниже).


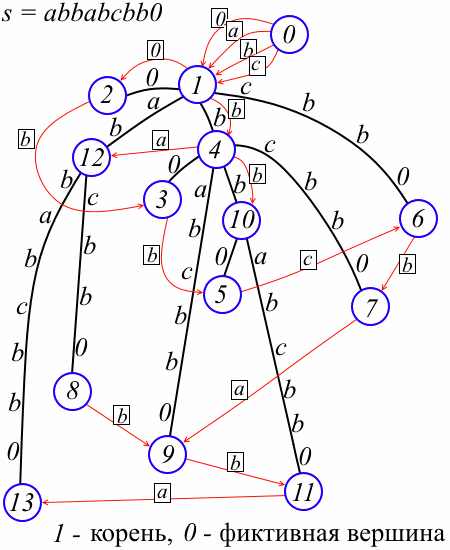
Таким образом мы имеем дополнительную структуру:

std::map<char, int> link[0..sz-1]; //префиксные ссылки

По определению в каждую вершину может вести не более одной префиксной ссылки, откуда заключаем, что link занимает O(n) памяти.

Предварительно оговорим одни технический нюанс представленной здесь реализации. Корень дерева – это вершина 1, а 0 – это фиктивная вершина такая, что link[0][a] = 1 для всех символов a; вдобавок par[1] = 0 и len[1] = 1. Фиктивная вершина не несёт особой смысловой нагрузки, но позволяет обрабатывать некоторые частные случаи единообразно. Ниже это будет разъяснено подробнее, а пока не обращайте на неё внимания. Приступим к описанию алгоритма вставки нового суффикса.

Алгоритм

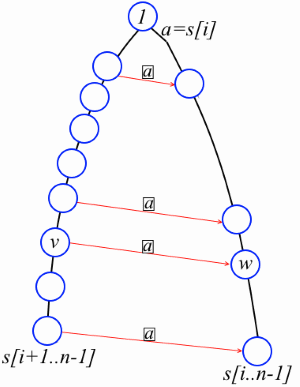Лемма. Пусть i – некоторое число от 0 до n-2. Рассмотрим суффиксное дерево строки s[k..n-1], где k <= i. Если w – некорневая вершина на пути от корня к листу, соответствующему s[i..n-1], то на пути от корня к листу, соответствующему s[i+1..n-1], есть вершина v такая, что s[i]str(v) = str(w) и link[v][s[i]] = w (смотрите рисунок).

Докажем это. Обозначим str(w) = s[i]t. По определению суффиксного дерева либо w — лист, либо у w есть как минимум два потомка. Если w — лист, то v — это лист, соответствующий строке s[i+1..n-1]. Пусть w не лист. Тогда найдутся некоторые различные символы a и b такие, что to[w][a] ведёт к одному ребёнку w, а to[w][b] к другому. Значит s[i]ta и s[i]tb – это подстроки s (как минимум одна из них начинается не в позиции i). Следовательно ta и tb – тоже подстроки и в дереве должна быть вершина v такая, что str(v) = t. Ясно, что v лежит на пути к листу, соответствующему s[i+1..n-1], и, по определению префиксных ссылок, имеем link[v][s[i]] = w.

Итак, положим мы имеем суффиксное дерево для строки s[i+1..n-1] и собираемся добавить лист для строки s[i..n-1] и сообразно этому обновить префиксные ссылки. Смотрите рисунок ниже. Обозначим через old лист, соответствующий s[i+1..n-1]. Место «стыковки» нового листа – это вершина w’, которая, возможно, ещё не создана. Через w обозначена вершина, лежащая непосредственно над w’ (если w’ уже есть в дереве, то w = w’ и в этом случае достаточно только добавить новый лист). Для простоты рассмотрим сначала случай, когда w не корень. По лемме найдётся вершина v на пути от old до корня такая, что link[v][s[i]] = w.


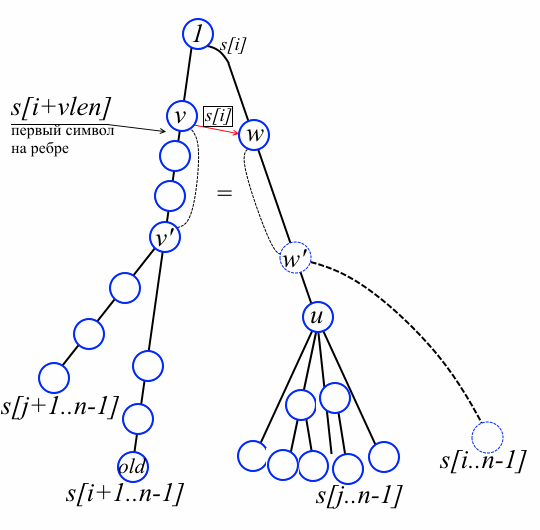
Факт 1. На пути от v к old нет вершин v’’ таких, что link[v’’][s[i]] определено. Пусть, от противного, v’’ – такая вершина. Тогда вершина link[v’’][s[i]] – предок w’ и, одновременно, потомок w (по определению префиксных ссылок). Но мы выбрали w как ближайшую вершину от места стыковки! Противоречие.

Наш алгоритм первым делом находит v и w. Заодно мы вычисляем в переменной vlen значение |str(v)|+1 и складываем в стэк path все пройденные вершины – они ещё пригодятся. Заметьте, что по окончании цикла s[i+vlen] равно первому символу на ребре от v к отпрыску v на пути к old (см. рисунок выше).

	int v, vlen = n - i, old = sz – 1;//в нашей реализации old – это последняя вершина
	for (v = old; !link[v].count(s[i]); v = par[v]) {
		vlen -= len[v];
		path.push(v);
	}
	int w = link[v][s[i]];

Факт 2. Вершина w’ уже присутствует в дереве тогда и только тогда, когда to[w][s[i+vlen]] не определено; в этом случае w = w’. Если немного помедитировать над рисунком выше и замечанием о значении символа s[i+vlen], это утверждение становится очевидным.

Факт 3. На пути от v до old есть вершина v’ такая, что s[i]str(v’) = str(w’), даже если w’ ещё не существует. Если w’ уже есть в дереве, то утверждение очевидно по факту 2 и v’ = v. Предположим w’ ещё только предстоит создать. Обозначим u = to[w][s[i+vlen]]. Выберем произвольный лист из поддерева с корнем u; пусть этот лист соответствует суффиксу s[j..n-1] для некоторого j. Ещё не вставленный суффикс s[i..n-1] и суффикс s[j..n-1] расходятся в «неявной» вершине w’. А вот листья, соответствующие s[j+1..n-1] и s[i+1..n-1], уже представлены в дереве и расходятся в некоторой вершине v’. Ясно, что s[i]str(v’) = str(w’), а значит v’ лежит на пути от v к old. На этом месте стоит в последний раз вглядеться в рисунок выше. Мы приступаем к основной части алгоритма.

Теперь, когда мы нашли w, наша задача найти место стыковки нового листа, т.е. фактически мы ищем len[w’] и вершину v’. В случае w = w’ достаточно присоединить лист к w и провести префиксную ссылку из old в этот лист. Рассмотрим сложный случай, когда w != w’, т.е. есть ребро из w по символу s[i+vlen]. Обозначим, опять, u = to[w][s[i+vlen]]. Мы последовательно достаём из стэка path вершины пока не найдём вершину v’ такую, что s[i]str(v’) = str(w’). Как мы определяем, что нашли нужную вершину? Пусть v₁, v₂, …, v_k – верхние вершины из стэка path причём v_k = v’ (смотрите рисунок ниже). Через a_p обозначим первый символ на ребре, следующем из v_p к потомку v_p на пути к old. Определим a₀=s[i+vlen]. Пусть t – метка на ребре от w до u. Символ t[len[v₁] + len[v₂] + … + len[v_p-1]] будем называть символом, соответствующим a_p на t. Так как w’ – это точка ответвления суффикса s[i..n-1] на ребре от w к u, символ a_k не равен соответствующему символу на t. С другой стороны, по той же причине для каждого p=0,1,…,k-1 символ a_p равен соответствующему символу на t. С рисунком это рассуждение станет понятнее:



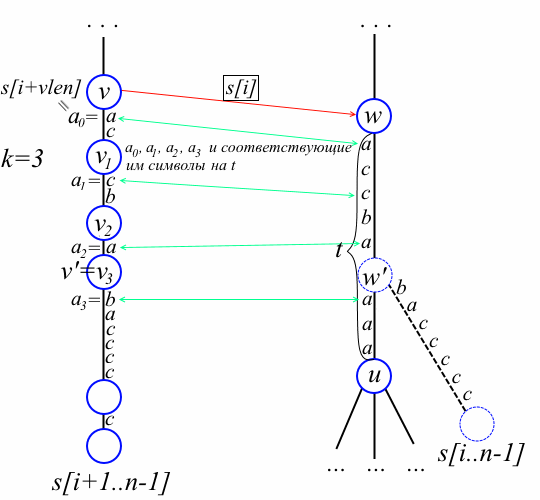
Полученное замечание является ядром упрощённого алгоритма Вейнера. Интересно, что нам достаточно сравнивать только первый символ на рёбрах с соответствующим символом на t, а не все символы. По-существу это простое наблюдение — это то, что заметили Бреслауэр и Италиано, а раньше почему-то никто не замечал. Осталось не забыть провести префиксную ссылку из v' в w' и префиксную ссылку из old в новый лист. Итак, алгоритм вставляет новый суффикс s[i..n-1] следующим образом:

	if (to[w].count(s[i + vlen])) { //если w != w’
		int u = to[w][s[i + vlen]]; 
		//sz – это новая вершина w’, которую мы создаём
		//т.к. w!=w', условие s[pos[u] - len[u]] == s[i + vlen] на первой итерации цикла истинно
		for (pos[sz] = pos[u] - len[u]; s[pos[sz]] == s[i + vlen]; pos[sz] += len[v]) {
			v = path.top(); path.pop(); //очередной кандидат на v’
			vlen += len[v];
		}
		Разбить ребро от w к u вершиной w’=sz; len[w’] = len[u]-(pos[u]-pos[sz])
		link[v][s[i]] = sz; //суффиксная ссылка из v’ в w’
		w = sz++; //устанавливаем w = w’ для вставки нового листа
	}
	//в этой точке переменная w содержит w'
	link[old][s[i]] = sz; //суффиксная ссылка из old в новый лист sz
	Присоединить лист sz к w; len[sz] = n – (i + vlen)
	pos[sz++] = n; //pos для листьев всегда равен n

Осталось рассмотреть частный случай, когда w – это корень. Эта ситуация полностью аналогична, но некоторые значения сдвинуты на единицу. Можно было бы, конечно, обработать этот случай отдельно, но с помощью фиктивной вершины сделать это проще и дополнительного кода писать не придётся. В этом месте важную роль играет тот факт, что par[1]=0, len[1]=1 и link[0][a]=1 для всех символов a. Таким образом цикл поиска вершины v обязательно оборвётся на вершине 0, а значение len[1]=1 обеспечит необходимый сдвиг на единицу. Разобраться в подробностях не составит труда и я оставлю это как упражнение. Надеюсь тайный смысл фиктивной вершины на этом должен проясниться. Объединяя всё вместе, получаем такое решение:

void attach(int child, int parent, char c, int child_len) //вспомогательный метод
{
	to[parent][c] = child;
	len[child] = child_len;
	par[child] = parent;
}
void extend(int i) //один шаг алгоритма; вызывать для i=n-1,n-2,...,0
{
	int v, vlen = n - i, old = sz - 1; 
	for (v = old; !link[v].count(s[i]); v = par[v]) {
		vlen -= len[v];
		path.push(v);
	} //по окончании цикла vlen = |str(v)|+1
	int w = link[v][s[i]]; 
	if (to[w].count(s[i + vlen])) { //если w != w’
		int u = to[w][s[i + vlen]];
		for (pos[sz] = pos[u]-len[u]; s[pos[sz]]==s[i + vlen]; pos[sz] += len[v]) {
			v = path.top(); path.pop(); //очередной кандидат на v'
			vlen += len[v];
		}
		attach(sz, w, s[pos[u] - len[u]], len[u] - (pos[u] - pos[sz])); //присоединить w'(=sz) к w
		attach(u, sz, s[pos[sz]], pos[u] - pos[sz]); //присоединить u к w'(=sz)
		w = link[v][s[i]] = sz++; //провести префиксную ссылку из v' в w'; установить w = w' для вставки нового листа
	} //в этой точке переменная w содержит вершину w'
	link[old][s[i]] = sz; //префиксная ссылка из старого листа к новому
	attach(sz, w, s[i + vlen], n - (i + vlen)); //присоединить новый лист sz к вершине w'
	pos[sz++] = n; //pos для листьев всегда равен n
}
void init()
{
	len[1] = 1; pos[1] = -1; par[1] = 0; //важно, что par[1] = 0 и len[1] = 1 (!)
	for (int c = 0; c < 256; c++)
		link[0][c] = 1;//из вершины 0 префиксные ссылки по всем символам ведут в корень
}

Оценка времени работы алгоритма

В заключении поймём почему вся описанная конструкция выполняет O(n) операций. Высотой вершины v назовём количество вершин на пути от корня к v. Напомню, что шаг алгоритма – это добавление нового суффикса в дерево. Обозначим через h_i высоту вершины, соответствующей самому длинному суффиксу на i-м шаге. Пусть k_i – это число вершин, пройденных от old к v на i-м шаге. Как изменяется значение h_i? Если ещё раз взглянуть на рисунок к лемме, поразмыслив, вы заметите, что h_i < h_i-1 – k_i-1 + 2. Число операций, выполненных на i-м шаге, пропорционально k_i, а значит, как мы только что заметили, O(h_i+1 – h_i + 2). Отсюда очевидно, что алгоритм выполняет O(2n + (h₁ – h₂) + (h₂ – h₃) + … + (h_n-1 — h_n)) = O(n) операций в сумме.

Небольшое оптимизационное замечание. Учитывая время доступа к мапам, время работы алгоритма Вейнера (так же как и Укконена) – O(n log m), где m – число различных символов в строке. Когда алфавит очень мал, вместо мапов лучше использовать массивы, чтобы сделать Вейнера действительно линейным.

Справедливости ради стоит отметить, что упрощённый алгоритм Вейнера (а классический и подавно) потребляет примерно в полтора-два раза больше памяти, чем Укконен. Также тесты показали, что упрощённый Вейнер работает примерно в 1.2 раза медленнее (тут он несильно уступает Укконену). Тем не менее все эти недостатки отчасти компенсируются простотой реализации Вейнера и отсутствием большого числа подводных камней.

Ссылки в хронологическом порядке

P. Weiner. “Linear pattern matching algorithms” 1973 – первая статья Вейнера, в которой введено суффиксное дерево и дан линейный алгоритм.

E. McCreight. “A space economical suffix tree construction algorithm” 1976 – более легковесный алгоритм построения суффиксного дерева.

E. Ukkonen. “On-line construction of suffix trees” 1995 – модификация алгоритма МакКрейта; самый популярный современный алгоритм.

D. Breslauer, G. Italiano. “Near real-time suffix tree construction via the fringe marked ancestor problem” 2013 (предварительная версия в 2011) – описание упрощённого алгоритма Вейнера в этой статье занимает один абзац (remark на 10й странице), а всё остальное посвящено другой близкой проблеме.

P.S. Спасибо Мише Рубинчику и Олегу Меркурьеву за помощь в тестировании алгоритма и предложения по улучшению кода.

P.P.S. В заключении привожу