Многие слышали о такой загадочной штуке, как энтропия. Обычно её называют мерой хаоса, мерой неопределённости и ещё прибавляют, что она непременно растёт. Я с огромной болью переношу употребление имени Энтропии всуе и решил, наконец, написать ликбез по этому вопросу.
Второе начало
Что будет, если бросить футбольный мяч на землю? Очевидно, он несколько раз подпрыгнет, причём каждый следующий раз на всё меньшую высоту, а затем и вовсе упокоится на земле. А что будет, если в горячий чай опустить металлическую ложку? Ложка нагреется, чай остынет. Ничего сложного, не так ли? В каждом из этих примеров направление протекания процессов кажется очевидным: мяч не может подпрыгивать выше и выше и даже не может вечно подпрыгивать до одной высоты, а чай не может ещё больше охладить ложку. Из таких житейских очевидностей были выведены два постулата (равноценных), каждый из которых может в равной степени называться вторым началом термодинамики:
— единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретого тела к более нагретому (постулат Клаузиуса);
— теплота наиболее холодного из участвующих в процессе тел не может служить источником работы (постулат Томсона), т.е. единственным результатом любой совокупности процессов не может быть превращение теплоты в работу.
Не зря эти два утверждения названы постулатами, они аксиоматичны, доказать их нельзя, они лишь подтверждаются своими следствиями и всем человеческим опытом.
Вроде всё и ясно: горячие тела остывают, холодные нагреваются, энергия рассеивается. Но как насчёт ещё одной задачки? Смешали по 1 моль водорода, азота и аммиака при температуре 500 oС в реакторе объёмом 10 литров в присутствии катализатора:

В какую сторону пойдёт реакция: образования аммиака или его разложения? Ммм… Кажется, нам нужно больше уравнений.
Цикл дедушки Карно
Знает каждый инженер
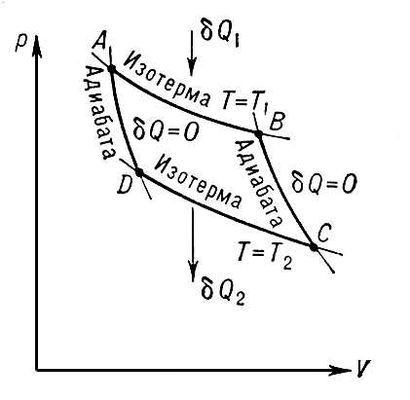
Цикл состоит из двух изотерм и двух адиабат. Его КПД равен:

где Qн и Qх — количество теплоты, полученное от нагревателя и отданное холодильнику соответственно, Tн и Tх — температуры нагревателя и холодильника.
Таким образом, полученная от нагревателя теплота расходуется на совершение работы, а затем часть работы расходуется на сжатие рабочего тела вновь по изотерме (работу в ходе адиабатных процессов оставим за скобками, она идёт за счёт внутренней энергии рабочего тела и мирно взаимоуничтожается). Чем меньше вторая величина, тем больше КПД.
А теперь приступим к мысленной гимнастике. Пусть у нас будут две тепловые машины с разными рабочими телами, работающие по циклу Карно. Причём первая работает равновесно (т.е., в любой момент времени система находится в равновесии, отсутствуют турбулентные потоки и прочие уменьшающие полезную работу и рассеивающие энергию штуки; работа равновесного процесса всегда больше работы неравновесного) и обратимо (т.е., процесс можно развидеть: провести его в обратном направлении так, чтобы и в системе, и в окружающей среде стало, как было; пример обратимого процесса — поглощение и испускание фотона одной и той же длины волны электроном, необратимого — нагрев тела), а о второй ничего неизвестно. Первая машина работает в обратном направлении, т.е. с помощью работы внешней среды над ней передаёт тепло от холодильника к нагревателю, вторая работает в обычном режиме. Холодильники и нагреватели машин соединены, а совершаемая работа равна по модулю:

т.е., работа, совершаемая второй машиной, идет на перенос тепла от холодильника к нагревателю первой (помним, что теплота, полученная телом, положительна, теплота, отданная окружающей среде, — отрицательна, работа, совершенная телом, — положительна, работа, совершенная над телом, — отрицательна; в формуле КПД все знаки уже учтены, поэтому теплоты берутся по модулю).
Пусть КПД второй машины больше, чем КПД первой, тогда с учётом (3) имеем:


Итак, в ходе всех перипетий и хитросплетений сюжета нагреватель получил теплоту QнI-QнII, а холодильник отдал теплоту QхI-QхII. Обе эти величины больше нуля, а суммарная работа обеих машин этому самому нулю равна. Т.е., кроме того, что теплота была перенесена от холодильника к нагревателю, не произошло больше ничего! Посмотрев ещё раз на постулат Клаузиуса, можно успокоиться и сказать, что такого не бывает.
Логично предположить, что условие (4) неверно, а значит, верно:

Если вторая машина работает равновесно и обратимо, то система становится симметричной, т.е. первую и вторую машину можно поменять ролями и ничего не изменится. Очевидно, этому случаю отвечает знак равенства. Отсюда можно сделать вывод о том, что КПД машины, работающей по циклу Карно, не зависит от природы рабочего тела. Таким образом, для установления формулы КПД достаточно рассмотреть любой частный случай. Уравнение (1) было получено из решения для идеального газа. Также можно сделать вывод о том, что КПД (как и работа) машины, работающей необратимо и неравновесно, меньше КПД машины, работающей обратимо и равновесно.
Из уравнения (1):

или

Алгебраическая сумма отношений теплот процесса к их температурам для цикла Карно равна нулю.
Любой циклический процесс можно разбить на множество бесконечно малых циклов Карно, и тогда предыдущее условие преобразится в:

Функции, изменение которых в результате любого циклического процесса равно нулю, называют функциями состояния. Их значение не зависит от пути процесса, а определяется только конечным состоянием.
Функцию состояния системы, изменение которой в ходе равновесного процесса равно отношению теплоты процесса к температуре его протекания, назвали энтропией:

(знак равенства относится к равновесным процессам, а знак больше — к неравновесным).
Если система изолирована, то есть не обменивается с окружающей средой ни веществом, ни энергией, то Q=0 (система не обменивается теплотой с окружающей средой), тогда:

или энтропия изолированной системы возрастает в неравновесных процессах и остаётся прежней в равновесных, или энтропия изолированной системы не убывает.
Amen. Мы дошли до той самой формулировки второго начала термодинамики!
Итого, из сказанного выше, никак нельзя сказать, что энтропия — мера чего-либо, это просто функция. Расти всегда она не обязана, никто не запрещает ей
По пути мы решили ту самую задачку про моли (да придётся пролистать назад, я и сам её забыл, всё-таки, термодинамика – захватывающая штука!). Чтобы решить, в какую сторону пойдёт реакция, нужно изолировать систему и посчитать изменение энтропии в ходе процесса: будет убывать – туда не пойдёт, будет возрастать – туда пойдёт, ну и остаётся вариант с равновесием, чтобы остановиться и передохнуть.
Что ж, с байкой про «энтропия всегда растёт» всё ясно: кто-то не дочитал «изолированной системы», но поспешил нести истину (с) в массы. А вот что с «мерой хаоса»? Я покажу вам ещё один подход.
The second father
Обратимся к статистике. Допустим, у нас есть N шариков, которые могут располагаться на двух разных уровнях относительно земли, ёмкость первого уровня N1, второго — N-N1. Сколькими способами можно разместить эти шарики? Очевидно, это число сочетаний без повторений (порядок размещения на уровне неважен, но каждый шар – индивидуальность и считается отдельно, можете представить их пронумерованными):

По сути мы записали число микросостояний (расположение конкретных шариков по уровням), через которые возможно достижение одного и того же макросостояния (N1 шарик находится на первом уровне относительно земли, а N2 шариков — на втором). Такое число называется термодинамической вероятностью. От обычной вероятности она отличается тем, что её забыли поделить на общее число микросостояний всех возможных макросостояний, т.е. если варьировать N1 и складывать все W при постоянном числе уровней и N.
Перейдём от букв к цифрам. Пусть уровня всё ещё 2, шариков всего 40, уровни при этом вырождены (т.е. шарикам без разницы, на каком именно находиться), а шарики случайным образом перемещаются между ними. Термодинамическая вероятность распределения «20 там и 20 там» равна 14.0*1010, а «19 к 21» – 13.3*1010. То есть шанс посмотреть и увидеть «20 к 20» всего в 1.053 раза больше, чем «21 к 19», хотя интуитивно мы воспринимаем распределение пополам гораздо более вероятным, чем перевес. Вот что теорвер животворящий делает!
Но поглазели и хватит, вернёмся к теме разговора. Термодинамическая вероятность тоже позволяет судить о пути протекания процесса: если мы идём из состояния (макросостояния), W которого ничтожно мала, к состоянию с огромным

где k – постоянная Больцмана.

Кхмкхм произведения равно/равен/равна сумме кхмкхм. Знакомое соотношение? И Больцману оно показалось знакомым! И он вывел на листе уравнение имени себя с постоянной имени себя. Последнюю, кстати, найти также несложно: мы не ограничивали никак до сих пор (и далее не будем) набор объектов, которые подчиняются этому уравнению, и для всех этих объектов постоянная одна и та же, значит, можно взять частный случай, посчитать постоянную для него и утвердить её кандидатуру. Частным случаем, кстати, был вновь выбран идеальный газ.
Обнаружив такую связь, можно определённо заявить, что с ростом энтропии растёт термодинамическая вероятность, то есть растёт количество вариантов на микроуровне, которые реализуют один вариант на макроуровне. Такое огромное число вариантов реализации одного состояния некоторые назвают хаосом, но я сделать это никак не возмусь. Весь этот «хаос» подчинен закономерностям и Великому Рандому, который не хаос, а именно что Господин Случай. Я бы назвал энтропию – с точки зрения вероятностного подхода – мерой инвариантности системы и вам советую поступать так же!
Дописанная пятая страница в wordе мне подсказывает, что пора закругляться, хотя хотелось бы ещё сказать пару слов о границах применимости энтропии, её характере и тепловой смерти Вселенной. Но это потом, а сейчас пора спать…
Литература
1. Герасимов Я.И. и др. «Курс физической химии», том 1 – Москва, из-во «Химия», 1964 г. – 624 с.
Комментарии (116)

superhimik
19.08.2016 09:57— Чтобы решить, в какую сторону пойдёт реакция, нужно изолировать систему и посчитать изменение энтропии в ходе процесса: будет убывать – туда не пойдёт, будет возрастать – туда пойдёт, ну и остаётся вариант с равновесием, чтобы остановиться и передохнуть.
Направление протекания химической реакции определяется не изменением энтропии, а изменением изобарно-изотермического потенциала (энергии Гиббса). В приведённом примере реакция сопровождается убываем энтропии, однако она замечательно протекает.
MoonGoose
19.08.2016 10:44Направление протекания химической реакции определяется двумя основными принципами:
1. в условиях возможности совершения системой работы над внешней средой (закрытая система) – максимумом этой работы, т.е. возможностью системы понизить свою энергию путем совершения работы (передачи тепла);
2. в условиях полной изоляции – возрастанием энтропии (прямо следует из второго начала т/д: энтропия изолированной системы в ходе самопроизвольных процессов не убывает).
Во втором случае критерием является рост энтропии, в первом случае – уменьшение функции Гиббса (она же изобарный потенциал, только в изобарно-изотермических условиях, тогда максимальная полезная работа меньше либо равна изменению энергии Гиббса, взятому с противоположным знаком) либо уменьшение функции Гельмгольца (в изохорно-изотермических условиях, та же приписка).
Конкретно к задаче в статье применимо нахождение изменения функции Гельмгольца (газовая фаза, объём реактора постоянен, температуру можно поддерживать постоянной) либо нахождение изменения энтропии в условиях изолированной системы. Что я и сделал для того, чтобы продемонстрировать применение второго начала. Функция Гиббса неприменима, т.к. в ходе реакции давление в системе изменяется (конкретно – уменьшается, сумма коэффициентов перед веществами в газовой фазе слева равна 4, справа – 2).
Тот же Герасимов стр. 114.
Pand5461
19.08.2016 12:57Интересно, что можно их объединить в один принцип возрастания энтропии замкнутой Вселенной — объединения системы и внешней среды.
В частных случаях более удобным эквивалентным условием будет убывание энергии Гельмгольца (тепловое равновесие со средой, жёсткая оболочка) и Гиббса (тепловое и механическое равновесие со средой).
MoonGoose
19.08.2016 13:10Я вам скажу даже больше: функции Гиббса и Гельмгольца и условия самопроизвольного протекания процессов, и все четыре термодинамических потенциала выводятся из объединения первого и второго начал термодинамики.

superhimik
19.08.2016 15:41Цитировать учебники по физхимии я тоже умею. :-)
К указанной задаче функция Гиббса вполне себе применима — посмотрите, пожалуйста, любой учебник и задачник по термодинамике, в которых выводится константа равновесия этой реакции. Там и будет рисунок сосуда с поршнем, в котором давление не изменяется.
MoonGoose
19.08.2016 15:50Ну не свою же мне термодинамику придумывать?! :)
Я это все писал к тому, что можно использовать изменение энтропии в качестве критерия. Вопрос о критерии решается заданием постоянных параметров ведь.
superhimik
19.08.2016 15:59— Я это все писал к тому, что можно использовать изменение энтропии в качестве критерия.
Так в том-то и дело, что нельзя. В указанной реакции энтропия убывает — это очевидно без расчётов. Но она термодинамически возможна из-за того, что идёт с выделением тепла. Поэтому я и напоминаю об изобарно-изотермическом потенциале: именно он служит критерием направления протекания реакции. Этому учат на первом курсе химфака.
MoonGoose
19.08.2016 16:19Вы систему забыли изолировать. В изолированной системе энтропия не может убывать. Убывает там энтропия очевидно только при постоянной температуре. Из-за выделения тепла в ходе реакции она спокойно может расти и при уменьшении количества молекул.

superhimik
19.08.2016 16:39Подождите, а где в условии вашей задачи говорится, что система изолированная?

MoonGoose
19.08.2016 19:13Там нет и обратного утверждения. Как нет оснований полагать, что процесс идёт при постоянной температуре и давлении.

superhimik
19.08.2016 19:44Так если нет условий, то и задача нерешаема.
Понимаете в чём дело. Химические реакции не проводят в изолированной системе — это никому неинтересно, важно уметь предсказывать направление в реальной системе. Поэтому и изучают изобрано-изотермический потенциал.
MoonGoose
19.08.2016 20:16Так я и не старался написать задачу для сборника задач по хтд. Мне всего лишь нужно было перейти от простой и очевидной ситуации к более сложной, требующей введения самого понятия энтропии.

superhimik
19.08.2016 20:54так просто ценность примера оказалась равной 0. Как говорится, тема сисек не раскрыта.
carpaccio
19.08.2016 19:12Энергия Гиббса это аналог энтропии для частного класса открытых систем (изобарно-изотермических).

katletmedown
19.08.2016 10:49+1Формулировок 2 начала ведь было достаточно много, я подозреваю. Мне нравиться такая.
Любой реальный самопроизвольный процесс является необратимым. [В.А.Кирилин, Техническая Термодинамика]

MoonGoose
19.08.2016 11:07Да, их достаточно много (12, насколько я помню). Причём все они эквивалентны, и каждую из них путём некоторых размышлений можно привести к любой другой. Существует даже целая книга, посвященная различным формулировкам второго начала и переходам от одной формулировке к другой (названия, к сожалению, не помню).
Во времена изучения курса химической термодинамики нашей любимой была:
Вечный двигатель второго рода невозможен [тот же постулат Томсона (он же лорд Кельвин)].

anderston
19.08.2016 11:31«Существует стрела времени»
Энтропия есть «информация» о состояниях. В ходе динамической эволюции энтропия остается неизменной вследствие унитарного характера такой эволюции. Именно поэтому я считаю уместным назвать динамику физикой существующего. Термодинамику в отличие от динамики следовало бы назвать физикой возникающего. Второе начало термодинамики подтверждает реальность изменения и вводит физическую величину (например, энтропию), наделяющую время выделенным направлением, или, если воспользоваться выражением Эддингтона, задающую «стрелу времени». Энтропия устанавливает различие между прошлым и будущим. Кроме того, термодинамика приводит к новой концепции времени как внутренней переменной, присущей системе. Такое понимание времени позволяет считать более «старым» (по сравнению с другим) то из двух состояний, которому соответствует большее значение энтропии. Интерпретация времени как внутреннего свойства физической системы выходит за рамки традиционного физического описания системы.
Илья Пригожин, «От существующего к возникающему»

ivkol
19.08.2016 11:57список литературы пополнить бы современными трудами. трактат все-таки

MoonGoose
19.08.2016 12:00Сомневаюсь, что с прошлого века там что-то сильно изменилось (правда, в сторону т/д никогда особенно и не копал), но если у вас есть на примете статьи или книги по данной теме, с радостью их почитаю и добавлю в статью.

Bas1l
19.08.2016 22:23Есть очень хорошая относительно новая статья в Nature Materials. Пдфа вроде в интернетах нету, но на подмогу всегда придет sci-hub.
Статья как раз про то, как поменялись (или должны поменяться) некоторые представления об энтропии в связи некоторыми находками. Например, пишет автор, в 1957 году впервые сделали очень показательное компьютерное моделирование.
Автор, кстати говоря, очень известный ученый. Аж статьи про него на википедии есть. А чтоб два раза не вставать, то качество ученого проверяется легко, надо всего лишь посмотреть на его профиль в google scholar, а в нем на специальный индекс, h-index.
MoonGoose
20.08.2016 00:28Спасибо за статью!
Прочёл, ничего с ног на голову не переворачивается, постулаты не пересматриваются. Если коротко: есть системы, которые самопроизвольно переходят из состояния видимого беспорядка (там в примере случайным образом ориентированные палочки) в видимый порядок (палочки ориентированы по одному генеральному направлению с некоторым разбросом) все остальные параметры при этом остаются теми же. Хочется сказать, что энтропия системы понизилась, но тут как раз стоит вспомнить, что энтропия != видимый порядок. До перестроения палочки обладали большим разнообразием вариантов углов поворота, но мешали друг другу двигаться в объёме, после перестроения же энтропия, связанная с возможностью поворота снизилась, но в то же время палочки приобрели гораздо большую свободу перемещения. То есть один вид «подэнтропии» компенсировал понижение другого вида «подэнтропии».
По этому принципу предлагается создавать материалы, которые самопроизвольно собираются.
ShabanovYT
19.08.2016 11:59-1Чтобы получить уравнения гидродинамики нужно взять Закон сохранения энергии — диф.ур., Закон сохранения импульса — диф.ур. и добавить к ним диф. ур. неразрывности. В 70-е годы прошлого было показано, что из них можно получить всю ТО.
Первые два уравнения можно объединить в одно: DE\ Dt = 0 ( полная производная энтропии по времени равна нулю).
Именно таким образом в каждой точке нашего мира протекают процессы.
MoonGoose
19.08.2016 12:23Первые два уравнения можно объединить в одно: DE\ Dt = 0 ( полная производная энтропии по времени равна нулю).
Именно таким образом в каждой точке нашего мира протекают процессы.
Можно ссылку на источник?

stanislavkulikov
19.08.2016 13:00Так и по итогу, энтропия — это всё-таки мера хаоса, но автору больше нравится называть её мерой инвариантности системы. И энтропия всё-таки всегда растёт, в изолированной системе конечно, но это уточнение никого не волнует.

MoonGoose
19.08.2016 13:05Называть вы можете что угодно как угодно, вопрос лишь в том, чем оно на самом деле является. Я как раз и пытался ответить на этот вопрос.
И пытался как раз донести ясность в понимании: в изолированной системе в ходе самопроизвольных процессов энтропия не убывает. Она может оставаться постоянной. Это как не «икс в квадрате больше нуля», а «икс в квадрате – неотрицательное число (на множестве действительных чисел)».napa3um
21.08.2016 17:22В современной науке от вопроса «как оно на самом деле» отошли к вопросу «как удобнее это интерпретировать в такой-то задаче». И очень давно. Именно потому попытка «сорвать покровы» и сформулировать «как оно на самом деле» вне контекста конкретной задачи выглядит наивной аппеляцией к Абсолютной Истине.

MoonGoose
21.08.2016 17:42В данном случае разночтений быть не может, по крайней мере в рамках термодинамики. Энтропию просто определили так. Если вы принимаете п = 3.1415 (прямо так), то не может быть разночтений, что в этой задаче оно 3, а в следующей 3.1 — уже договорились и условились, что 3.1415.
napa3um
21.08.2016 17:50Да, математика — лишь язык описания физики, к ней критерии фальсификации физических теорий не применимы. В физике без явно или неявно подразумеваемой задачи (эксперимента над реальностью) вообще никакая теория смысла не имеет. Возможно, ваши задачи кажутся вам единственными существующими в науке, потому и ваши формулировки кажутся вам «очевидными» и «однозначным».

FransuaMaryDelone
22.08.2016 09:04Если вы принимаете п = 3.1415 (прямо так), то не может быть разночтений, что в этой задаче оно 3, а в следующей 3.1 — уже договорились и условились, что 3.1415.
Стопэ! Я не договаривался и не уславливался с теми, у кого пи — рациональное число.

3cky
19.08.2016 13:01Из всех объяснений сущности энтропии для меня самым понятным стало приведенное в «Элегантной Вселенной» Грина: энтропия — это число всевозможных перегруппировок элементов данной физической системы, при которых ее общий вид не изменяется. То есть если в комнате бардак, то переложенный из тумбочки на стол носок никак общего вида обстановки не изменит, а вот в идеально прибранной комнате он сразу бросится в глаза.

alexeynos
19.08.2016 13:22На GT уже была хорошая статья про энтропию:
«Энтропия? Это просто!» https://geektimes.ru/post/246406/
Более простая для понимания, IMHO, правда почти без формул.
MoonGoose
19.08.2016 13:24Мне она как раз не нравится. Имеет право на существование, но не очень научна, по моему мнению. Есть такая проблема: чем больше используешь аналогий, тем меньше понимаешь, о чём вообще говоришь.

mrMidas
19.08.2016 16:54-1Математическая формула ровно такая же аналогия как и прочие. Разница между ними в том, что «бытовые» основаны на подобии свойств феноменов, а математические аналогии на логической связанности свойств и качеств. Говоря иначе, математические аналогии более абстрактны и тем универсальнее. Понятность тех или иных аналогий никак не связаны с сутью самих аналогий и зависит от типа мышления конкретного индивида.
Но матаналогии имеют одну особенность, которая нередко выливается в баги на некоторых платформах, т.е. у конкретных индивидов, — транзитивность. Она позволяет сильно экономить ресурсы при формировании матмодели, но она же требует воспроизведения всего контекста при выводах.
В данном случае, при сохранении истинности во всей статье, при выводе возникла кумулятивная ошибка. А началась она тут:
Любой циклический процесс можно разбить на множество бесконечно малых циклов Карно
. Тут мы вполне обоснованно транзитивно перешли от системы как единицы к системе как сумме единиц. Дальше всё моделирование идёт относительно единичного элемента. Так что в конце, при выводе, надо было выполнить обратное преобразование. На словах оно выполнено, а вот контекстно нет. Это дало неверное предположение о причине неточности понимания термина. Дело не в том что кто-то пропустил изолированность, а дело в том в системе не может быть изолированных элементов и при этом система не имеет верхнего предела. Поэтому всегда для системы W, состоящей из n элементов и имеющей Sn как сумму, добавление ещё одного элемента изменит S так, что S' > Sn. Так что если строго, то никакой ошибки в утверждении что энтропия в системе только растёт нет. Ошибка возникает в контексте применения этого утверждения.
MoonGoose
19.08.2016 19:25Спасибо за комментарий!
Но даже при добавлении к системе элемента суммарная энтропия не обязана расти, остаётся вариант с идеальным кристаллом при 0 К, тогда она не изменится (недостижимый, конечно же). Но это будет открытая система. Обычно же рассматривают либо изолированные, либо закрытые системы, в них добавление элемента невозможно, а для закрытых систем энтропия может даже уменьшаться за счёт роста энтропии в окружающей среде.
И всегда есть вариант с равновесным обратимым адиабатным процессом, когда энтропия не изменяется.

alexeynos
19.08.2016 14:30С помощью аналогий там как раз доходчиво объяснено главное: что энтропия — это свойство не самОй системы, а мерило нашего знания об этой системе. И что если мы о замкнутой системе в любой момент времени знаем всё, то её энтропия всегда будет равна нулю какой бы сложной система не была.

Bas1l
22.08.2016 01:35Мне кажется, это совершенно неверное понимание энтропии. Ошибочное, можно сказать. Энтропия в статистической механике задается через статистический ансамбль систем. Стандартных ансамбля три—микроканонический, канонический и большой канонический ансамбль. Стандартная (и якобы простая) формула S = k lnW, которую привел автор, вообще-то, справедлива только для микроканонического ансамбля, да и то там не все так просто.
Да, в феноменологической термодинамике, которую рассказывают в школе и на первых курсах институтов, энтропия—это типа свойство системы (одной). Но любая попытка вменяемо ее определить математически начиная с законов Ньютона или квантовой механики (а не через странные феноменологические постулаты)—притом так, чтоб выполнялись постулаты термодинамики—заканчивается определением энтропии через статистические ансамбли.
Да, можно кое-как определить такую энтропию через одну систему. Например, рассматривая много слабо взаимодействующих подсистем (вот, мол, они сформируют ансамбль). Так делают Ландау и Лифшиц в томе 5. Или можно рассматривать одну систему в течение какого-то промежутка времени. И типа система засэмплирует какой-то кусок фазового пространства за это время (то есть можно будет построить распределение ее состояний, то есть ансамбль систем). Но это все рассуждения на пальцах.
Да, есть информационная энтропия с очень похожим законом и почти таким же смыслом и они сильно связаны. Но чтоб выполнялись постулаты термодинамики, энтропию нужно определять через ансамбль систем, то есть через фазовое пространство. От того, что вы точно узнаете в данный момент все о системе, энтропия статистической механики не поменяется—она не определена через одну систему.

alexeynos
19.08.2016 15:56Знаем все необходимые характеристики (положение, скорость, направление, закон движения, и т.д.) микрообъектов при изучении макрообъекта в системе. Например, азота водорода и аммиака в Вашем примере. Понятно, что этого мы полностью знать не можем, поэтому и энтропия ненулевая. Но когда шарики заведомо разложены по полочкам и, например шарик скатывается с верхней полки на нижнюю 1 раз в секунду, то энтропия равна нулю, ведь мы это точно знаем.

MoonGoose
19.08.2016 19:12Нет. Даже если мы будем знать о системе всё, энтропия у неё будет ненулевая (если это не идеальный бездефектный кристалл при 0 К). Энтропия – функция состояния системы, т.е. без разницы, каким образом система в данное состояние пришла, энтропия будет одна и та же. Вот мы о системе ничего не знали, кроме энтропии, – вот всё узнали, но энтропия не изменилась, потому что не изменилось состояние системы. Даже если мы будем, пытаясь узнать текущие параметры системы и её составляющих, влиять на систему, энтропия не станет равна нулю, потому что абсолютный ноль недостижим.

Pand5461
19.08.2016 23:25Если мы будем знать о системе всё, то энтропия у неё всё-таки будет нулевая, т.к. гипотетически мы тогда можем сделать, например, электромагнитное поле очень сложной конфигурации, и всю тепловую энергию системы перевести в полезную работу.
В этом один из парадоксов классической физики.
И дело даже не в демоне Максвелла (его проблема решается постулированием, что при создании полей столь хитрой конфигурации мы в окружающую среду выпустим больше энтропии, чем заберём из системы). Дело в теореме Лиувилля о сохранении фазового объёма гамильтоновой системы.
Даже если мы начальное состояние знаем не совершенно точно, а с некоторой погрешностью — эта погрешность, согласно Лиувиллю, в замкнутой системе не должна изменяться со временем. В классическом примере газа, который в начальный момент времени занимает половину сосуда, а потом свободно расширяется — с точки зрения классической механики, вот этот вот заведомо пустой объём в половину сосуда меняется со временем предсказуемым образом. А значит, газ как бы всегда занимает только половину сосуда, т.е. его энтропия не меняется.
Если ввести неопределенность Гейзенберга, то всё сразу становится на свои места, то бишь убегает в непредсказуемом направлении при попытке точно узнать состояние.
MoonGoose
19.08.2016 23:52Здесь у нас, похоже, два мира сталкиваются, разлетаются к чертям, а на их месте возникает непонимание.
Я нисколько не силён в статистической физике и с разбегу пытаться в ней что-то понять, открыв статью на википедии, мне крайне сложно. С удовольствием почитаю публикацию по этому вопросу, если вы её напишите.
У вас, видимо, понятие энтропии задано каким-то другим образом. В моем (и не только) понимании, энтропия введена как функция состояния, зависящая только от текущих макропараметров (p, V, T, природа тел, состав системы). Просто заметили, что если ввести функцию, изменение которой в ходе процесса равно deltaQ/T, то как в точку ни приди, значение этой функции одно и то же. Прикольно? Прикольно! Надо использовать. Назвали энтропией. А чтобы считать было легче задали ещё 0 при 0 К. Понаставили кучу экспериментов, проверили – расхождений нет, работает нормально.
Pand5461
20.08.2016 00:56Да не, определения энтропии эквивалентны в термодинамике и статфизике.
Просто одно дело, когда вы состояние определяете термодинамически тремя-четырьмя параметрами: 1 моль графита при атмосферном давлении и внутренней энергии E.
И другое — когда механически: атом углерода номер 1 с координатами (0,0,0) и скоростью (250,100,312), ..., атом углерода номер 6,022x1023 с координатами (1,1,1) и скоростью (-250,-100,-312).
В первом случае подходящих микросостояний чёртова прорва, во втором — одно, с точностью до сдвига по времени, если мы в рамках гамильтоновой механики.
Вывод 1: по формуле S = k ln(W) энтропия любого точно известного микросостояния равна в точности нулю.
Вывод 2: энтропия является характеристикой не состояния системы, а набора параметров, которые выбраны существенными для описания ансамбля состояний.
MoonGoose
20.08.2016 11:21Но вот вы описали одно точно одно интересующее (или реально существующее в данный момент) микросостояние, это микросостояние реализует одно какое-то макросостояние. То, что вы знаете, в каком микростоянии находилась/находится система, не отменяет того, что это же макросостояние может быть реализовано другими микросостояниями. Термодинамическая вероятность на то и вероятность, что считает все возможные микросостояния, которыми реализуется одно макросостояние. Вы не уничтожили своим знанием возможность осуществления других микросостояний и не уменьшили W.
Вот если мы говорим об идеальном бездефектном кристалле при 0 К, то там в принципе возможно лишь одно состояние, поэтому W = 1, S = 0. Либо у вас системы волшебные и переход из одного микросостояния в другое невозможен, но для волшебных систем пусть пишут волшебную термодинамику :)
А вывод 2 противоречит определению энтропии. Нельзя ввести энтропию как функцию состояния, а потом сказать, что она от состояния не зависит. Это шизофрения какая-то :)
Pand5461
20.08.2016 13:42Нам надо определиться с терминологией.
Что такое макросостояние?
Я его отождествляю с понятием статистического ансамбля:
Статистическим ансамблем физической системы называется набор всевозможных состояний данной системы, отвечающих определённым критериям.
Если критериев столько же, сколько степеней свободы в системе, то, очевидно, в ансамбле будет, в лучшем случае, одно состояние. И никто не запрещает такой ансамбль вводить, если очень хочется.
Физический смысл нулевой энтропии в таком ансамбле — это то, что при полном знании микросостояния возможно сконструировать механизм, полностью переводящий тепловую энергию в полезную работу.
это микросостояние реализует одно какое-то макросостояние
В моём понимании, это не так.
Даже если рассматривать только равновесные ансамбли, в которых система описывается тремя параметрами — их по меньшей мере пять — NVE (заданы число частиц N, объём V, внутренняя энергия E), NVT (температура T), NPT (давление P), ?VT (химический потенциал ?), ?PT.
Одно и то же микросостояние можно рассматривать как элемент разных ансамблей. Энтропия определяется тем, сколько в рассматриваемом ансамбле других состояний, эквивалентных данному.
Пример — произвольное микросостояние моля жидкой воды при параметрах тройной точки. Если мы рассматриваем макросостояние в смысле NVT — то моль пара при тех же условиях не будет реализовывать то же самое макросостояние. А если в смысле NPT — то моль пара и моль льда будут эквивалентны начальному.
Конечно, если не находиться в точке фазового перехода или ввести во все ансамбли дополнительный параметр — фазовый состав — то в термодинамическом пределе энтропия будет одна и та же, к какому бы ансамблю мы данное микросостояние не отнесли.
MoonGoose
20.08.2016 13:54Что такое макросостояние?
Я его отождествляю с понятием статистического ансамбля:
Вот здесь у нас критическое расхождение. Точнее у статфизики и термодинамики, получается. Макросостояние – система с определенным набором макро же характеристик – термодинамических параметров: p, V, T, состав. Т.е. не произвольно выбранных критериев, а свойств, проявляющихся на уровне системы и определяющих физическое состояние системы, которые вполне могут не проявляться при разбиении этой системы на подсистемы, либо вообще отсутствовать.
Термодинамические параметры — температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины:
— однозначно определяющие термодинамическое состояние системы;
— не учитывающие молекулярное строение тел; и
— описывающие их макроскопическое строение.
savenya
21.08.2016 21:28Можно ведь взять десяток железных шариков разного цвета и для них подсчитать энтропию определенного состояния (1 черный 9 белых), а можно для них подсчитать энтропию 10 шарообразных тел из железа определенной массы при определенных давлении и температуре, это будут две категорически различных величины.
Поэтому, мне кажется, что энтропия сильно зависит от выбора параметров и их числа (считай частиц: либо шарики, либо набор частиц в, например, кристалле)
MoonGoose
21.08.2016 21:44Вам кажется. Нужно, чтобы макросостояние (определение выше) было одно и то же.

Pand5461
21.08.2016 23:13Поэтому, мне кажется, что энтропия сильно зависит от выбора параметров и их числа (считай частиц: либо шарики, либо набор частиц в, например, кристалле)
Хорошее замечание.
Энтропия, как и внутренняя энергия, энтальпия и свободная энергия, определена с точностью до константы. Энтропия 10 цветных железных шариков будет складываться из энтропии S0 просто 10 кусков железа плюс Scolor, связанной с раскраской. Если рассматривать шарики, ничем кроме цвета не отличающиеся, при неизменных внешних условиях, то константу S0 можно опустить.
С цветами, конечно, нужно игнорировать ещё различие в энтропии красок разного цвета. Но именно у железа есть параметр, который не требует добавления другого вещества и может отличать внешне одинаковые два куска — это намагниченность. Намагниченный кусок железа обладает меньшей энтропией, чем размагниченный — это называется магнитокалорический эффект.

Pand5461
20.08.2016 13:54Либо у вас системы волшебные и переход из одного микросостояния в другое невозможен
Я ж говорю, это парадокс классической физики с её детерминизмом — из заданного микросостояния замкнутая система не может перейти абсолютно в любое другое. А множество тех микросостояний, в которые она может перейти (а также тех, которые успела пройти до момента наблюдения), имеет нулевую лебегову меру.
Нельзя ввести энтропию как функцию состояния, а потом сказать, что она от состояния не зависит.
Ну да, плохо сформулировал на ночь глядя. Надо: энтропия является характеристикой не (микро)состояния системы как такового, а набора параметров, до которых мы редуцируем описание этого состояния.

NailGafurov
19.08.2016 19:06Простите, опечатка?
переход теплоты от менее нагретого тела к более нагретому

worldmind
19.08.2016 19:49Я может чего-то не понял, но как я понимаю когда говорят что энтропия всегда растёт имеют ввиду энтропию Вселенной, которая видимо замкнутая система.
Видимо в теории она может оставаться постоянной, но на практике эту возможность можно игнорировать.
А вот использование её как меры хаоса действительно мутнова-то, часто под хаосом понимают некое бытовое понятие, например, машина ржавеет это непорядок, хотя, если я правильно помню, реакция окисления как раз с ростом энтропии проходит.
MoonGoose
19.08.2016 20:26Чтобы понять, что же имеют в виду, когда говорят «энтропия растёт», нужно спросить говорящего :) Маловероятно то, что он задумывается о судьбах Вселенной.
Да, на практике процессы неравновесные и, зачастую, необратимые, знак равно можно отбросить, но для математической строгости его оставляют.
Конкретное явление коррозии железа идёт с уменьшением энтропии: там газообразный кислород (у газов энтропия относительно велика) переходит в твердый оксид (без влаги, просто окисление железа) или в гидроксид (в присутствии воды), которые – как твёрдые тела – обладаю много меньшей энтропией. Тепло реакции отводится в окружающую среду, где энтропия растёт.
savenya
20.08.2016 01:09Еще одним образом энтропию можно представить как множитель, который характеризует сколько «несвободной» энергии (теплоты) находится в системе:
F=U-TS,
G=H-TS=U+PV-TS.
То есть, F и G — свободные энергии Гельмгольца и Гиббса, соответственно, которые могут теоретически перейти в работу (например, химическую, электрическую и тд), а G, имея слагаемое PV, еще и в механическую.
Можно сказать, что энтропия — мера рассеяния энергии из «полезной», «концентрированной» в «бесполезную», «рассеянную».
Собственно слово «энтропия» — др.-греч. ???????? — поворот, превращение («энергии» в «тепло»)
MoonGoose
20.08.2016 11:28Да, и так можно. При этом, что интересно, система, стремясь уменьшить свою свободную энергию, может либо совершать работу/отдавать тепло, либо наращивать энтропию.

savenya
21.08.2016 21:39Хорошая формулировка, приятно видеть человека, распространяющего здесь тайное учение об началах термодинамики

Voliker
21.08.2016 10:45В термодинамике не учитываются гравитационные взаимодействия как минимум, а на мегауровне ещё много всяких забавных штук. Плюс никто ещё толком не доказал, что вселенная — замкнутая система. Поэтому и о тепловой смерти вселенной можно на время забыть.

worldmind
21.08.2016 11:57> Плюс никто ещё толком не доказал, что вселенная — замкнутая система.
думаю она является таковой по определению, если есть какой-то источник энергии, то он включён во вселенную.
Про гравитацию не понял.napa3um
21.08.2016 12:27Вселенная — не замкнутая и не изолированная система, т.к. применение этих формализмов к космосу в самых больших масштабах потребует фиксации геометрических свойств пространства. А вселенная, как известно, расширяется, потому энтропия в ней не обязательно увеличивается (может и увеличивается, но это ещё нужно доказать). Замкнутость в термодинамическом смысле не совсем совпадает с замкнутостью в «бытовом/философском» смысле о включении в систему «всего сущего».

Bas1l
19.08.2016 22:29У меня вот такой вопрос. Вся термодинамика, теоретически, должна быть выводима из микроскопических законов поведения систем. Более того, достаточно каких-то очень общих микроскопических характеристик. И многие определения можно давать на микроскопическом уровне. Например, как вы написали, S = k ln(W). Это определение относится ко всему фазовому пространству (то есть W—это количество всех состояний системы вообще. До реакции, после реакции, во время реакции. Всех вообще). Так вот, вопрос: как энтропия вообще может меняться со временем, если она определена через все фазовое пространство? То есть, грубо говоря, через ансамбль систем.

MoonGoose
19.08.2016 23:29Дело как раз в том, что термодинамика на микроуровне перестаёт работать. Все ключевые понятия термодинамики к микромиру неприменимы, а выводится всё, по сути, из трёх её начал, которые постулаты и не охватывают большого числа физических явлений (например, первое начало: dQ = dU + delta A, т.е. это частный случай закона сохранения энергии, теплота превращается в энергию и работу и наоборот, но здесь нет ни слова о таких вещах, как переход массы в энергию и наоборот, перенос энергии излучением, которые очень важны на микроуровне и при релятивистских скоростях). Поэтому термодинамика достаточно ограничена в применении при масштабировании вверх и вниз.
Вы немного не так поняли смысл термодинамической вероятности W. Это все варианты состояний составляющих, при который макросостояние (т.е. вся система) находится в одном конкретном состоянии с заданными макропараметрами p, V, T, S, q и т.д. Это не количество всех состояний системы вообще, а число вариантов одного состояния.
Bas1l
22.08.2016 03:29+1Да, я не совсем точно написал. Но на самом деле, я знаю ответ на свой вопрос (мне кажется). И мне кажется, что у вас в статье есть ошибки. И я как раз и хочу на них указать.
Да, положим, что W—это все варианты, которые удовлетворяют внешним условиям. (Кстати, для начала нужно еще подумать, какие это внешние условия. Не все же из них независимые.) Положим, у нас есть изолированный идеальный газ. Для него мы зададим V и Т (и N, конечно). Давление и внутреннюю энергию U и все остальное можно вывести (через уравнение состояния и т.п.). Газ, конечно, находится в состоянии термодинамического равновесия с окружающей средой, то есть резервуаром (и у него, конечно, такая же температура T). Проблема в том, что контакт со средой означает, что энергия нашего газа U—это средняя внутренняя энергия. А текущая внутренняя энергия E колеблется вокруг средней энергии U (да, система изолирована и макроскопически энергией не обменивается. но она же в тепловом равновесии с резервуаром. то есть отдельные молекулы могут менять энергию из-за столкновения со стенкой, граничащей с резервуаром. иначе как бы мы дошли до состояния термодинамического равновесия?). И мы даже знаем, как текущая внутренняя энергия E колеблется вокруг средней внутренней энергии U: по закону канонического распределения (очень похожего на распределение Максвелла-Больцмана)! Плотность вероятности получить текущую энергию E пропорциональна exp(-E / k T) или равна С*exp(-E / k T) (см. также здесь). А среднее значение U = <E*С*exp(-E / k T)>. Но что это значит? Что система может оказаться в состоянии с любой энергией E. А это значит, что число W ее микросостояний с заданными внешними условиями бесконечно. То есть энтропия S по вашему определению S = k lnW всегда бесконечна. И так будет для любой системы. Это, конечно, проблема.
Но я решу ее за вас! Ошибка в том, что формула S = k lnW—это очень частная формула. В ней W означает число состояний, когда заданы N, V, и совершенно точное значение E. То есть когда нет вообще никакого обмена энергией с окружающей средой, нет окружающей среды, и нет теплового равновесия с ней. Множество всех систем с такими N, V и E называется микроканоническим ансамблем. По-другому, N, V и E задают фазовое пространство систем. И энтропия определяется по формуле S = k lnW для такого фазового пространства, и только для него.
Есть еще канонический и большой канонический ансамбли. В каноническом ансамбле как раз предполагается наличие резервуара, теплового равновесия и определенной температуры, а не энергии. Но формула для энтропии другая: S = — k \sum_i p_i ln (p_i), где p_i—вероятность попасть в определенное микросостояние (с энергией E_i). Эта вероятность как раз и равна С*exp(-E_i / k T). Если энергии непрерывны, то вместо суммы—интеграл, вместо вероятностей—плотность вероятности. Более того, это не определение энтропии, а следствие из определения для микроканонического ансамбля и некоторых рассуждений (например, чтоб работали постулаты термодинамики).
Микроканонический и канонический ансамбли называются еще, как ни странно, NVE и NVT ансамбли.
Теперь можно вернуться к моему вопросу. Теперь мы знаем, что нужно сосредоточиться на NVE ансамбле, а W определена для всего фазового пространства системы, когда заданы N, V и E. И вот это-таки значит, что энтропия системы никогда не будет меняться. Да, в этом пространстве есть состояния, в которых газ находится в одной половине объема. Они тоже включены в энтропию.
А что же тогда с возрастанием энтропии? И вообще, как определить энтропию для одной системы, а не для ансамбля?
Представим, что мы начинаем с состояния (в NVE ансамбле), где газ в одной половине сосуда. И при динамике системы он, конечно, постепенно займет весь сосуд. Мы можем сгруппировать все состояния NVE ансамбля по тому, какой реальный текущий объем Vr занимает газ (через convex hull, к примеру). И для всех Vr посчитать W(N, V, E, Vr). Интеграл этой функции по Vr даст W(N, V, E). И, конечно, число состояний в группе, которая занимает весь объем, будет максимальным и вообще такие состояния будут занимать почти все фазовое пространство при N стремящимся к бесконечности (важно, что тогда и V будет стремиться к бесконечности, если мы хотим сохранить N/V). То есть W(N, V, E, Vr = V) почти равно W(N, V, E). То есть наш газ будет расширяться, Vr будет меняться со временем и расти. Текущая W(N, V, E, Vr), которую мы меряем по фазовому пространству тоже будет расти. И когда Vr дорастет до V, оно там и остановится. То есть газ уже никогда не покинет эту часть фазового пространства. Это и есть смысл возрастания энтропии в микроканоническом ансамбле—для любой дополнительной переменной есть значение, которое доминирует в фазовом пространстве, то есть занимает почти все фазовое пространство. И если вы начинаете с состояния вне этой области, вы всегда дойдете до нее и там и останетесь. (примерно так и написано в википедии). Спонтанное упорядочивание твердых палочек из другого комментария—это другой пример (только параметр—это степень упорядочивания). В принципе, это примерно то, что всегда имеют в виду (и вроде бы, что вы имели в виду в статье и комментариях), но более предметно.
Для NVE ансамбля можно доказать форму основного термодинамического тождества. Разницу между энтропиями для разных Vr можно тогда посчитать через это тождество, представив, что Vr меняется квазистатически от V/2 до V. Это стандартная даже школьная задача.
Это все рассуждения для микроканонического ансамбля. Возрастание энтропии в NVT ансамбле—это похожий, но все-таки другой вопрос. Так же, как и доказательство основного термодинамического тождества.
MoonGoose
22.08.2016 11:14-1Давайте отделять
мух от котлеттермодинамику от статфизики. Хотя бы потому, что терминология разнится (выше уже в комментариях выяснили, что макросостояние статфизика не понимает, понимает ансамбли, но они не тождественны макросостояниям). Поэтому, разговаривая о термодинамике, используем термодинамику.
Вы начали свои размышления с того, что назвали закрытую систему (обменивается энергией, не обменивается веществом) изолированной (не обменивается ни тем, ни другим), и предположили, что полная внутренняя системы непостоянна, а подчиняется Больцмановскому распределению, что с точки зрения термодинамики значит:
а) система не изолирована,
б) меняются макросостояния (потому что внутренняя энергия — функция состояния и для одного макросостояния принимает одно значение).
Далее, W — это все варианты, удовлетворяющие текущим термодинамическим переменным, характеризующим макросостояние. Т.е. тд вероятность опирается на внутренние параметры, а не на внешние. Или называйте по-другому или используйте что есть.
Pand5461
22.08.2016 12:33+1В термодинамике нет никаких микросостояний.
Есть четыре потенциала, которые однозначно зависят от своих характеристических переменных и состава. При возможности реакции, минимизация этих потенциалов по степени протекания реакции при постоянных значениях характеристических переменных определяет равновесное состояние системы.
Какие именно переменные определяют термодинамическое состояние, вы упорно отказываетесь говорить.
Скажу за вас для системы известного состава с постоянным числом частиц в отсутствие внешних полей:
— если рассматривается замкнутая система, то это любые два из тройки (объём V, энтропия S, внутренняя энергия E), потенциал E
— система в нетеплопроводящей, но «мягкой» оболочке — любые два из тройки (давление P, энтропия S, энтальпия H), потенциал H
— система в жёсткой оболочке в тепловом равновесии со средой — любые два из тройки (объём V, температура T, энергия Гельмгольца F), потенциал F
— система в тепловом и механическом равновесии со средой — любые два из тройки (давление P, температура T, энергия Гиббса G), потенциал G
Задание параметров сверх этого будет избыточным, а меньше — недостаточным.
MoonGoose
22.08.2016 13:051. Ну как-то нужно понимать энтропию с точки зрения статистического подхода, поэтому введены. А так да, предметом являются макросистемы, их состояния и превращения.
2. Это уже достаточно высокий уровень абстракции. Не ими едиными.
3. Цитировал же определение выше:
Термодинамические параметры — температура, плотность, давление, объем, удельное электрическое сопротивление и другие физические величины:
— однозначно определяющие термодинамическое состояние системы;
— не учитывающие молекулярное строение тел; и
— описывающие их макроскопическое строение.
4. Вы грубо аппроксимировали все системы идеальным газом.
Pand5461
22.08.2016 15:39То вы хотите отделять термодинамику от статфизики, то понимать энтропию с точки зрения статистического подхода. Определитесь уже.
И к чему определение термодинамических параметров? Состояние-то как через них определить? Вот 1 моль вещества с химической формулой H2O при температуре 273,15 К, плотности 1 г/см3 и давлении 1 Мбар — это хорошее определение термодинамического состояния?
MoonGoose
22.08.2016 16:28Я хочу, в первую очередь, использовать одинаковую аксиоматику. Понятно, что без элементов статфизики не выведешь, но и понятно, что, называя (или подразумевая) разные вещи одинаковыми именами, одного и того же не получишь. Хотите стат методами получить ту же энтропию, что и классически — используйте те же исходные.
К тому, что считать веществом в том же состоянии, а что — в разных.
Если вычеркнуть плотность (не угадали, да и избыточна), и принять формулу воды, как краткое описание её свойств (теплоемкостей, энтальпий испарения и плавления и т.д.), то да. Не хорошее, а достаточное для описания тд состояния.
Pand5461
22.08.2016 23:14Хотите стат методами получить ту же энтропию, что и классически — используйте те же исходные.
Всё же сделано уже до нас.
С аккуратными определениями в термодинамике веке в 17-18, я думаю, не слишком заморачивались. Состояние и есть состояние, интуитивно понятно. Когда дошли до термодинамических потенциалов, стало понятно, что разница всё-таки есть — при разных условиях имеет смысл определять состояние в разных переменных. Что, впрочем, не мешает другие параметры состояния вычислить путём дифференцирования термодинамического потенциала. В итоге, как задать состояние — скорее дело вкуса, главное, чтобы оно было задано полным набором характеристических переменных какого-либо потенциала, тогда всё будет однозначно.
Больцман потом выразил энтропию через термодинамическую вероятность — и оказалось, что если в замкнутой системе определить 1/T = (dS/dE)V, то получается очень красивое следствие, что если две системы в жёсткой оболочке привести в тепловой контакт, то максимальной вероятности соответствует выравнивание температур. Т.е. всё как в нормальной термодинамике. Потом Гиббс вывел распределение для малой подсистемы замкнутой системы (канонический ансамбль) — из него как частные случаи вывелись распределение Максвелла и Больцмана. Кроме того, получилось, что если взять микроканонический ансамбль (замкнутую систему) и канонический ансамбль с той же средней энергией — то температуры их (для первого — по определению через производную, для второго — как параметр распределения) тоже совпадают. Ну и средняя энтропия всех состояний из канонического ансамбля просто равна энтропии микроканонического ансамбля с той же температурой. Другие термодинамические характеристики, конечно же, тоже можно выразить через средние по ансамблю, и они будут согласованы с определениями из феноменологической термодинамики.
Но возникает важное следствие — по определённому микросостоянию нельзя точно сказать, каким параметрам канонического ансамбля оно соответствует. Поэтому я и прошу настойчиво объяснить, что же всё-таки понимать под вашим «макросостоянием».
Если макросостояние — это состояние с заданной энергией и объёмом, то ОК, в микросостоянии худо-бедно объём можно определить, как предлагает Bas1l, а энергия определена однозначно, тогда и энтропию можно определить через соответствующий микроканонический ансамбль. Если же задана температура и ещё что-нибудь — то уже плохо, так как температуру из микросостояния проблематично вытащить.
MoonGoose
22.08.2016 23:34Это состояние с заданным всем, что относится к системе в целом: U, V, p, T, S, состав и другие характеристики, если таковые необходимы для однозначности. Все, что является функцией состояния, для макросостояния задано одновременно (напрямую или через соответствующие закономерности).
Обколются своей статфизикой, потом термодинамику не понимают.napa3um
22.08.2016 23:37> Обколются своей статфизикой, потом термодинамику не понимают.
Просто попытайтесь допустить, что вы сами кое-чего недопонимаете.
MoonGoose
22.08.2016 23:45Мне не нужно допускать, что я что-то недопонимаю, я это знаю (что что-то не понимаю, понимаю неверно). Например, статфизику. Уже подумываю искать учебник. Единственное, что я понимаю, — это юмор, да.
napa3um
22.08.2016 23:51Судя по ветке, вам хорошо бы было допустить, что собеседники сообщают вам новую информацию, а не соревнуются с вами в риторике. Ещё вам стоит быть чуть менее уверенным в собственном чувстве юмора — эта уверенность как раз противоположна чувству юмора. Ну а мне, в свою очередь, стоит потренироваться в дозировании пафоса в своих комментариях. (Вроде, всех озадачил, можно идти спать.)

FransuaMaryDelone
23.08.2016 11:41+1Обколются своей статфизикой, потом термодинамику не понимают.
«Обколются своей статфизикой» — моя тонкая душевная организация страдает, читая такое от автора трактата об энтропии.

Bas1l
23.08.2016 02:12Почти со всем в вашем комментарии соглашусь (вот и меня упомянули). Но замечу, что температуру-таки можно вытащить по микросостоянию. Потому что температура (в классической системе, по крайней мере) все равно оказывается мерой кинетической энергии молекул или атомов, так что ее можно найти через среднеквадратичную скорость, к примеру.
А вот что точно тяжело определить по микросостоянию, так это равновесные параметры системы. Потому что по микросостоянию бывает очень тяжело сказать, насколько мы близки к равновесной области фазового пространства (в данном ансамбле с данными параметрами).
Например, есть такая штука, как glass transition. Вот вам два обзора про нее. Так вот, при приближении макроскопических параметров системы к параметрам ideal glass transition время релаксации системы растет в бесконечность. То есть нужно ждать бесконечно долго, пока система дойдет до равновесного состояния. И по микросостоянию системы в данный момент вы никогда не скажете, срелаксировала система или нет (долетела ли система до равновесной части фазового пространства или нет). И равновесные параметры, соответственно, по микросостоянию не определите. Если время релаксации все еще не очень большое при данных макроскопических параметрах и текущем микросостоянии, вам нужно следить за динамикой микросостояния, чтоб оценить, срелаксировали вы или нет. Но может быть так, что время релаксации составляет пару десятков лет наблюдения или пару сотен лет работы компьютера (если это симуляция), и вы никогда не узнаете, дошли вы до равновесия или нет.
Pand5461
23.08.2016 11:06+1Я объём написал потому, что самопроизвольное ужимание газа вдвое при нормальных условиях уже при сотне молекул будет случаться раз в миллион лет, а уменьшение кинетической энергии вдвое у той же сотни молекул будет не таким уж редким событием, по опыту молекулярного моделирования.
Стёкла — это показательный пример того, что всё фазовое пространство быстро не обойти. И при этом они получаются довольно легко даже из простеньких силикатов. А взять какие-нибудь полимеры — там же термодинамическое равновесие рядом не валялось! Просто потому, что локальных энергетических минимумов глубиной ~100-200kT громадное количество, а выход из них занимает десятилетия.

Bas1l
23.08.2016 03:21Вы начали свои размышления с того, что назвали закрытую систему (обменивается энергией, не обменивается веществом) изолированной (не обменивается ни тем, ни другим)
Не совсем. Я исходил из того, что иногда даже про изолированную систему говорят, что она в контакте с heat bath. Это делается для того, чтоб разрешить парадокс Лошмидта. Вот википедия пишет про изолированную систему: «If, however, the stochastic behavior of the molecules and thermal radiation in real enclosing walls is considered, then the system is in effect in a heat bath». Тогда \delta Q у любого куска стенки равна нулю, внешней работы и обмена частицами нет, но энергия может немного плавать. Моя цель была в основном показать, что ваша формула энтропии (S=k lnW) справедлива только для NVE ансамбля. Помимо этой цели, действительно, нет смысла менять договоренность о том, что изолированная система—это NVE ансамбль (а парадокс можно разрешить и без этого). Но и в этом случае все мои пункты остаются в силе. А именно:
1. S=k lnW справелива только для NVE ансамбля
2. Для NVT ансамбля формула другая
3. S определена для всего фазового пространства с заданными параметрами (либо NVE, либо NVT, либо большой канонический). К примеру, для идеального газа (положим, в NVE ансамбле) она включает даже состояния, когда газ находится в одной половине объема. Или даже в одной трети. То есть вообще-то энтропия никогда не меняется. Это и есть парадокс Лошмидта. На него я намекал в своем самом первом вопросе. Точнее, парадокс Лошмидта даже более общий. Вроде бы он будет работать, даже если не выполняется принцип равновероятности микросостояний. И вроде бы и в NVT ансамбле.
4. Тем не менее, парадокс Лошмидта можно объяснить, даже в NVE ансамбле. Как—я попытался рассказать выше. Это делает и википедия, в параграфе «Suppose we have an isolated system whose macroscopic state is specified by a number of variables...»
Далее, W — это все варианты, удовлетворяющие текущим термодинамическим переменным, характеризующим макросостояние.… Т.е. вероятность опирается на внутренние параметры, а не на внешние
Тут я вас не совсем понимаю. Я уже давал ссылки на NVE, NVT и NV\mu ансамбли (микроканонический, канонический, большой канонический). Я так понимаю, в изолированной системе вам нужно задать только N, V, E. Равновесные значения остальных внутренних и внешних параметров вы выведите (через уравнение состояния). И энтропию. Действительно, в термодинамике говорят, что энтропия—это функция состояния. А в стат физике—что она определена по всему фазовому пространству. Тут противоречия (почти) нет, потому что равновесная область фазового пространства занимает почти все фазовое пространство (в математическом смысле, все остальное—множестно меры нуль в пределе N->infinity). Поэтому область равновесная. То есть энтропия по всему пространству почти совпадет с энтропией по равновесной области. Если вы дошли до равновесной области из неравновесного состояния, то никогда не выйдете. Это и есть закон возрастания энтропии (если энтропию параметризовать еще каким-то параметром в зависимости от куска фазового пространства, где мы находимся, как я уже два раза писал). В этом и заключается объяснение стрелы времени.
Давайте отделять термодинамику от статфизики
Нет, не давайте. Любая физическая теория более высокого уровня должна выводиться из теории более низкого уровня. Термодинамика должна выводиться из законов Ньютона или квантовой механики. Так же, как уравнения Навье-Стокса выводятся из законов Ньютона. Она не должна начинаться со странных феноменологических постулатов, если у нас уже есть теория более низкого уровня. В общем-то, называть их постулатами даже неправильно.
К сожалению, «постулаты» из законов Ньютона вывести не так легко, поэтому в школе и на первых курсах университетов их просто записывают без доказательства (а вот уравнение Навье-Стокса вывести проще, поэтому его всегда выводят). Кроме того, ими можно кое-как пользоваться без понимания вывода из законов Ньютона (или квантовой механики). На этом их преимущества заканчиваются. А начинаются недостатки. А именно: они не дают точных определений; не дают глубокого понимания того, что происходит; из них не понять их границ применимости; даже не понятно, что каждый из постулатов значит. Пример, опять же—формула S=k lnW. Все ее пишут, но не все помнят, что она для NVE ансамбля. И уж еще более редко пишут формулу для NVT ансамбля (между прочим, она в итоге совпадет с формулой A=U-TS, где A—свободная энергия Гельмгольца, но тогда ее тоже нужно правильно определить в NVT ансамбле, через статистическую сумму).
Поэтому если определения термодинамики не совпадают с определениями статфизики, то это проблема. И проблема либо в определениях термодинамики (и только термодинамики), либо в «постулатах» термодинамики. На самом деле, определения совпадают, но только в своих границах применимости и если все делать очень аккуратно. Ну и с учетом того, что определения термодинамики, прямо скажем, мутные.
разговаривая о термодинамике, используем термодинамику
Короче, разговаривая о термодинамике без статфизики мы с большой вероятностью ни о чем осмысленном вообще не разговариваем (шутка. хотя на самом деле нет, не шутка)
MoonGoose
23.08.2016 15:58Уговорили, верю. Уравнение Больцмана имеет достаточно жесткие границы применимости – записано.
Спасибо вам и Pand5461 за столь терпеливое и достаточно подробное объяснение (без иронии, уже начал читать учебник статфизики, не забью, надеюсь).
А теперь о том, почему я так упирался. Термодинамика и энтропия в частности имеют большое количество экспериментальных данных и подтверждений. Я как химик больше, чем эксперименту не верю ничему, соответственно, работающую теорию и работающие определения считаю верными, пока не доказано обратное. Когда вы выводите энтропию с помощьюэльфийской магииансамблей и статфизики и она не совпадает с тем, что заведомо работает в реальном мире, я начинаю подозревать, что
а) у нас разная терминология;
б) вы вывели какую-то другую величину, но назвали её энтропией (то есть эта величина не будет работать так же, как классическая энтропия, не может её заменить).
Соответственно, я стараюсь всеми силами либо вернуться к известной мне терминологии, либо проинспектировать свойства «вашей» энтропии и указать на то, что она себя ведет не как классическая.
Какой бы «неправильной» ни была термодинамика, выводимая из желудей и спичек, а не из законов Ньютона или квантмеха, она работает, причём достаточно хорошо. Законы Ньютона и квантмех ведь тоже ниоткуда не выводятся, но тоже работают.
Pand5461
23.08.2016 19:14Аккуратнее с терминами — уравнение Больцмана в статфизике обычно используется в другом смысле :)
На самом деле, «вывод» энтропии в статфизике не слишком хорош в методическом плане. Потому что исторически её не выводили, а доказали, что если вводить именно так, то по свойствам она будет совпадать с привычной термодинамической энтропией в замкнутой системе. В тех ансамблях, где энергия не задана точно, вероятность W тоже точно не определена. Но можно взять энтропию в смысле среднего: ?S? = k?ln W? = k ?pi ln Wi = (как легко видеть) = -k ?pi ln pi. Свойства по-прежнему будут совпадать со свойствами термодинамической энтропии. Никакой эльфийской магии.
То, что энтропия зависит от информации наблюдателя — как я уже говорил, физически это имеет смысл, т.к. наблюдатель при увеличении своего знания о системе «открывает» для себя новые способы извлечь из неё энергию. И это подтверждается, например, магнитокалорическим эффектом. В чисто тепловой машине намагниченный кусок железа от размагниченного не отличается, и при нагревании от 0 до 300 К они ведут себя одинаково. Поэтому экспериментатор без магнитометра не имеет причин приписать им разные состояния или разную энтропию. Но из намагниченного можно вытянуть дополнительную полезную работу, при этом он, конечно, частично или полностью размагнитится и увеличит свою энтропию.
MoonGoose
23.08.2016 22:01Не нравится всё же мне эта «информационная» энтропия.
Рассматривая тот же магнитокалорический эффект, я бы вполне обошёлся классикой. Как я уже упоминал, энтропия определена абсолютно, и вроде бы, не учитывая слагаемое энтропии, связанное с различной ориентацией спинов электронов, термодинамика ошибается. Но. Абсолютная энтропия обычно не нужна, нужно лишь её изменение, поэтому:
а) пусть есть процесс, не затрагивающий магнитные свойства системы, тогда \delta S = Sпосле — Sдо = (Sпосле просто + Sпосле магнитная составляющая) — (Sдо просто + Sдо магнитная составляющая) = Sпосле просто — Sдо просто, т.к. Sдо магнитная составляющая = Sпосле магнитная составляющая;
б) процесс, затрагивающий магнитные свойства: \delta S = Sпосле — Sдо = (Sпосле просто + Sпосле магнитная составляющая) — (Sдо просто + Sдо магнитная составляющая).
«Дополнительную» работу извлечь всё так же можно, информационных свойств энтропия не проявила.
Pand5461
24.08.2016 01:03Информационные свойства энтропия тут проявляет в том, что просто кусок железа и намагниченный кусок железа — это разные вещи. Если вы провели случайным куском железа над иголкой, а она к нему подлетела — это вовсе не значит, что он намагничен. Примерно с той же вероятностью её атомы могли удачно оттолкнуться от стола, где она лежала, и с гораздо большей — стол могло толкнуть слабым землетрясением. К тому моменту, как вы достоверно установите, что эта чёртова железяка всё-таки намагничена, вы уже выделили тепла уже больше, чем T?Sмагн, так что пожалуйста, используйте свою свежеобнаруженную свободную энергию.

Pand5461
19.08.2016 23:43то есть W—это количество всех состояний системы вообще
Не всех вообще, а соответствующих заданному условию. Например, если есть трёхуровневая система из 2 (полагаемых различимыми) частиц с энергиями 0, E и 2E, то при рассмотрении зависимости W от полной энергии W(E) = 2 (одна частица на уровне E, другая на 0), а W(2E) = 3 (либо одна частица на 2Е, другая на 0, либо две частицы на Е).
В случае числа частиц, устремленного к бесконечности, и условий в виде «температура T, объём V» так явно не выписать, но смысл, в целом, тот же — с точки зрения довольно общего условия огромное число микросостояний идентичны.

warlock13
20.08.2016 13:20+1Это проблема конкретного определения энтропия. То есть это не совсем та энтропия получается. Разумеется, физическая энтропия должна быть определена для конкретного микросостония. Эта проблема с энтропией — она из тех проблем статистической физики, которые разрешаются квантовой механикой, где матрица плотности — аналог ансамблей в классике — с необходимостью появляется уже при описании одиночной системы (не ансамбля), если она запутана с окружением (то есть на самом деле всегда).

warlock13
20.08.2016 14:24+1В общем, подлинную стройность статфизика обретает только в своей квантовой ипостаси.

savenya
21.08.2016 21:41В общем, следуя Сасскинду, энтропию можно назвать скорее мерой нашего «незнания» о системе, ведь если мы знаем состояние каждой частицы, то это автоматически становится макросостоянием, и обращает энтропию в ноль)))

warlock13
22.08.2016 10:58+1Есть два вида энтропии: одна связана с незнанием, другая не связана. Корректно определить последнюю в классической статфизике не удаётся (либо ноль получаем, либо бесконечность). Эти энтропии связаны друг с другом, они имеют много общего, и нередко первая может быть важнее второй — в конкретной задаче. Однако, если мы хотим иметь второй закон термодинамики в виде, применимом к физическим системам независимо от наличия и характеристик некоего "знающего" субъекта, нам нужно иметь возможность приписать неэкстремальную энтропию микросостоянию. Такую энтропию, энтропию микросостояния, иногда называют "физической" — когда нужно подчеркнуть отличие от энтропии, связанной с незнанием (несмотря на то, что последняя также рассматривается физикой).
Квантовая механика даёт возможность определить такую "физическую" энтропию — через понятие смешанного состояния. Оказывается, микросостояния бывают двух разновидностей — чистые (описываются волновой функцией) и смешанные (описываются матрицей плотности). И оказывается, что есть соответствие между системой в смешанном микросостоянии и ансамблем систем в чистых состояниях, то есть между "физической" энтропией и энтропией как мерой незнания. Но не изоморфизм: вместо решения задачи о системе, находящейся в смешанном состоянии можно решать эквивалентную задачу о ансамбле систем в чистых состояниях, но не любую задачу об ансамбле систем в чистых состояни можно представить как задачу о системе в смешанном состоянии.
Такое положение дел объясняет, почему результаты статистической механики, полученные для ансамбля, нам удаётся успешно применять для конкретных систем (в конкретном микросостоянии).
Pand5461
22.08.2016 11:32Я правильно понимаю, что в КМ не требуется вводить закон возрастания энтропии в замкнутой системе (в смешанном состоянии)?
Ведь если газ занимает объём V (на границе пусть отражающие стенки), то не может в ходе эволюции состояния возникнуть ситуации, когда в объёме V/2 плотность строго обращается в нуль.
warlock13
22.08.2016 11:51Я правильно понимаю, что в КМ не требуется вводить закон возрастания энтропии в замкнутой системе (в смешанном состоянии)?
Нет, вот эта трудность остаётся и в квантовой механике: если не вводить никаких дополнительных соображений, то энтропия в замкнутой системе остаётся постоянной.

warlock13
22.08.2016 11:58Но если добавить хотя бы минимальную незамкнутость (декогеренцию, излучение), то энтропия перестаёт сохраняться. Накладывая затем несимметричные начальные и/или конечные условия, соответствующие наблюдаемой "стреле времени", мы получаем закон возрастания энтропии (или наоборот: принимая в качестве дополнительного закона возрастание энтропии можно отличить какие условия начальные, а какие — конечные).

Pand5461
22.08.2016 12:41Если что-то о системе известно, значит, уже незамкнутость имеет место.
В классике тоже, конечно, можно запретить неинвазивные измерения — но там можно даже по их результатам восстановить «истинное» состояние системы.

warlock13
22.08.2016 12:04Ведь если газ занимает объём V (на границе пусть отражающие стенки), то не может в ходе эволюции состояния возникнуть ситуации, когда в объёме V/2 плотность строго обращается в нуль.
Может, так же как и в классической механике: берёте начальное состояние, когда в объёме V/2 плотность строго обращается в нуль, эволюционируете его до состояния, когда газ занимает объём V. А затем просто переворачиваете всё задом наперёд: законы квантовой механики позволяют это делать так же, как и законы классической механики.
То есть факт ненаблюдения таких процессов в реальности нетривиален и требует для объяснения доолнительных соображений.

EFG
20.08.2016 11:08Тень на второе начало термодинамики бросает возможность применения ректенн для радиочастотного «приема» теплового излучения любых тел и выпрямления более 0% в постоянный ток. Жаль исследований, опубликованных в интернете, крайне мало. На русском языке примечательно «ИЗУЧЕНИЕ ВОЗМОЖНОСТИ СОЗДАНИЯ ЭФФЕКТИВНОГО ИЗОТЕРМИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ НИЗКОТЕМПЕРАТУРНОГО РАССЕЯННОГО ТЕПЛА НА ОСНОВЕ РЕКТЕНН. Шифр: Ректенны.», но информация в этой презентации очень скудная.

MoonGoose
20.08.2016 11:30А как это бросает тень на второе начало?

EFG
20.08.2016 13:16Пассивное электронное устройство, принимающее равновесное тепловое излучение в замкнутой системе и часть этого излучения преобразующее в постоянный ток, серьезно конфликтует с вторым началом. При этом совершенно не противоречит радиоэлектронным принципам: согласованная антенна на 2-20Тгц, резонансный умножитель напряжения и выпрямитель для этой частоты не являются недостижимой сложностью для современной микроэлектроники. Только вот размеры антенн и требуемая добротность умножителя создают проблему количества и площади этих элементов, ориентировочно миллиарды на кв метр чтобы получить 1вт мощности.

MoonGoose
20.08.2016 13:28До тех пор, пока не удастся преобразовать всё тепло без потерь в работу, второе начало никак не нарушится.

warlock13
20.08.2016 14:27+1Обычно в таких ситуациях оказывается, что просто учли не все тонокости, и на самом деле всё собранное будет неизбежно рассеиваться с потерями.
ShabanovYT
20.08.2016 13:09я как-то изобрел вечный двигатель: В герметичном цилиндре находится газ. Молекулы газа непрерывно соударяются и их скорости… разные. По-видимому математическое ожидание скорости молекулы соответствует средней температуре газа… Если цилиндр поставить вертикально всегда будет происходить гравитационное разделение молекул по скоростям. Не зависимо от внешних источников тепла, теплопроводности стенок и т.д.
Теперь помещаем в цилиндр элемент Пельтье и пользуемся дармовой энергией пока существует Вселенная.
— Не смог найти ответ на простой вроде бы вопрос: изменяется ли в реальности скорости молекул после столкновения?
В теории, если считать молекулы идеальными шариками, вроде не должны меняться. а вот что происходит в реальности непонятно. Это вопрос критически важен для осуществимости вышеописанного вд.
MoonGoose
20.08.2016 14:18Молекулы газа подчиняются Больцмановскому распределению по кинетической (равно тепловой) энергии.
Конечно меняются. Суммарный импульс остаётся постоянным, скорости таковыми оставаться не обязаны (если частицы одинаковой массы, постоянной будет сумма скоростей, векторная, конечно).

Pand5461
20.08.2016 14:25Не меняются. Но не взлетит. Носители заряда при движении вверх по проводам тоже гравитацией тормозятся :)
napa3um
20.08.2016 13:21Теперь ждём от автора формулировок по энтальпии.

MoonGoose
20.08.2016 13:27Там всё намного проще: H тождественно равно U + p*V. В дифференциальном виде: dH = dU + p*dV + V*dp. В изобарных условиях при отсутствии других видов работ, кроме работы расширения: dQ = dU + p*dV = dH, т.е. тепловой эффект процесса равен изменению энтальпии, которое – в силу того, что H – функция состояния (внутренняя энергия, давление и объём зависят только от текущего состояния системы и не зависят от пути, которым мы в это состояние пришли) – зависит только от начальных и конечных точек системы.
napa3um
20.08.2016 13:32«Я бы назвал энтропию – с точки зрения вероятностного подхода – мерой инвариантности системы и вам советую поступать так же!» — имелось ввиду что-нибудь такое же фундаментальное, формулы мы умеем смотреть в учебнике и сами.

MoonGoose
20.08.2016 14:10Да нет в ней ничего фундаментального. Лень было кому-то писать каждый раз dU + p*dV, решил сократить, заменил на dH по аналогии с изохорными процессами (там dQ = dU). Когда-то теплосодержанием называли, но это корявый термин, от него уже отказались. Можно H считать полной-преполной энергией системы (с учётом возможности совершения работы расширения, этакая аппроксимация произведения pV до потенциальной энергии, где давление будет интенсивным параметром, а объём – экстенсивным).

raid
20.08.2016 20:53-1>> Дописанная пятая страница в wordе мне подсказывает, что пора закругляться…
Не останавливайтесь!

atya
21.08.2016 10:47-1Основное противоречие термодинамики. Главный недостаток традиционных представлений о теплоте виден в очевидной противоречивости основных её понятий — теплоты и энтропии. Это противоречие связано с математическими понятиями полного дифференциала и функции состояния. Типичным примером функции состояния является внутренняя энергия W термодинамической системы, например, единицы массы газа. Это означает, что внутренняя энергия представляет собой однозначную функцию параметров газа, в частности, давления p и объёма V. Поэтому изменение внутренней энергии в каком-либо процессе не зависит от характера его, а определяется начальным и конечным состояниями газа. Так, в процессах а и б (рис. 6.1), в которых начальные 0 и конечные 1 состояния газа одинаковы, одинаковыми будут и изменения внутренней энергии. Математически это означает, что функция W(p,V) дифференцируема в заданном интервале изменения параметров p и V, и малое приращение внутренней энергии DW является её полным дифференциалом, определяемым частными приращениями от изменения каждого из параметров Dp и DV.
Очевидно, что если процесс замкнут, т. е. если по завершении его газ возвращается в исходное состояние (такие процессы в термодинамике называют также круговыми процессами или циклами), то изменение внутренней энергии в нём, подсчитанное как интеграл по замкнутому контуру, будет равно нулю. Это означает, что извлечь внутреннюю энергию из газа в каком-либо замкнутом термодинамическом процессе над ним не представляется возможным.
Энтропия S системы в традиционной термодинамике также определяется как функция состояния, а её приращение как полный дифференциал от приведённой теплоты: dS = ?Q/T, где ?Q — бесконечно малое приращение теплоты, T —абсолютная температура газа. В то же время для различных процессов — изохорного и изобарного — приращение энтропии подсчитывается по разным формулам:
S1 – S0 = CV ln(T1 /T0 ) — для изохоры,
S1 – S0 = Cр ln(T1 /T0 ) — для изобары;
здесь CV и Cр — теплоёмкости газа при постоянном объёме и постоянном давлении соответственно. Поскольку для газа Cр > CV, оказывается, что одному и тому же изменению температуры в изобарном процессе соответствует большее изменение энтропии, чем в изохорном. Это обстоятельство противоречит определению энтропии как функции состояния.
В противоположность внутренней энергии и энтропии, теплота в классической и современной термодинамике предстаёт функцией процесса, а не состояния; т.е. элементарное количество тепла ?Q, сообщаемого системе в процессе малого изменения её состояния, не является полным дифференциалом dQ, что нашло отражение и в обозначении ?Q этой величины. Иными словами, для перевода системы из одного состояния в другое с помощью различных термодинамических процессов ей нужно сообщать, вообще говоря, различные количества тепла. Тем самым фактически утверждается принципиальная возможность извлекать тепловую энергию из ничего путём организации подходящего цикла. Это обстоятельство грубо противоречит первому началу термодинамики.
MoonGoose
21.08.2016 11:07Из одной и той же точки в другую одну точку нельзя одновременно придти и по изобаре, и по изохоре, т.е. цикл, состоящий только из изобары и изохоры, невозможен.
Иными словами, для перевода системы из одного состояния в другое с помощью различных термодинамических процессов ей нужно сообщать, вообще говоря, различные количества тепла. Тем самым фактически утверждается принципиальная возможность извлекать тепловую энергию из ничего путём организации подходящего цикла.
Неверный логический переход. Это означает, что изменение теплоты по замкнутому контуру может быть не равно нулю.
savenya
21.08.2016 21:53Человек попытался вывести уравнение адиабаты (PV^gamma=const) или ее константу (gamma=Cp/Cv), у него не вышло.
А логический подход и правда неверен, ибо пытался подсчитать изменение энтропии в разных процессах, и она, очевидно, для них неодинакова

savenya
21.08.2016 22:00Недавно, около года назад, читал статью о несимметричности некоего квантовомеханического процесса во времени, что само по себе уже является весьма неортодоксальным. То есть это было какое-то преобразование, по сложности установления примерно как несимметричный бета-распад кобальта в 60-х (который, в итоге, привел к теоретическому выводу нейтрино), хотя по достоверности сильно уступал ему. Очень интересно если кто-то, во-первых, напомнит что это было, а, во-вторых сможет прокомментировать, ведь это, по определению квантовомеханическая «стрела времени», которая, насколько я знаю квантовую механику, там невозможна, а значит открывает некоторые горизонты т.н. «Новой Физики»

warlock13
23.08.2016 23:09Ничего не могу сказать насчёт упомянутых вами исследований, но могу сказать насчёт стрелы времени и симметрии законов.
Для стрелы времени несимметричности недостаточно. Точнее они вообще напрямую не связаны. Стрела времени как часть фундаментальных законов требует отказа от детерминизма. Если зная начальное состояние вы можете (в принципе) предсказать эволюцию и, таким образом, конечное состояние, а равно для каждого конечного состояния определить предшествовавшую эволюцию и начальное состояние, то обязательно найдётся симметрия, меняющая начальное и конечное состояние местами. Она может быть сложной — как CPT-симметрия в квантовой механике, но это не играет роли. Только нарушение детерменизма даёт стрелу времени — в случае квантовой механики это означает прежде всего неунитарность оператора эволюции, что не согласуется с современными научными данными. Поэтому наиболее перспективно искать "стрелу времени" как эмерджентное явление (важными современными ислледованиями в этом направлении являются исследования т. н. декогеренции), связанное с космологическими условиями (мы знаем, что начальное состояние Вселенной было низкоэнтропийным и что это необходимое условие для появления стрелы времени).


FransuaMaryDelone
цикл Карно красивее на ST-диаграмме (рис. с Википедии)

GoldJee
Но рисовать ее до введения понятия энтропии нелогично.