
Квантизированная Лена привлекает внимание
Например, старый добрый формат GIF использует палитру, максимум на 256 цветов. Если вы захотите сохранить серию своих селфи как gif-анимацию (кому бы это надо было), то первое, что вам, а точнее программе, которую вы будете для этого использовать, надо будет сделать – создать палитру. Можно использовать статическую палитру, например web-safe colors, алгоритм квантизации получиться очень простым и быстрым, но результат будет «не очень». Можно создать оптимальную палитру на основе цветов изображения, что даст результат наиболее визуально похожий на оригинал.
Алгоритмов создания оптимальной палитры несколько, каждый имеет свои плюсы и минусы. Я не стану утруждать читателя нудной теорией и формулами, во первых мне лень, во вторых большинству это не интересно – статью просто пролистают, рассматривая картинки.
Далее вас ждёт
Итак – метод медианного сечения. Он прост до безобразия. Первым делом надо из всех уникальных цветов изображения составить RGB куб. Далее рассечь его по самой длинной стороне. Например, диапазон красного у нас от 7 до 231 (длина 231-7=224), зелёного от 32 до 170 (длина 170-32=138), синего от 12 до 250 (длина 250-12=238), значит, будем «резать» куб по синей стороне. Получившиеся сегменты так же рассекаем по длинной стороне и т.д. пока не получим 256 сегментов. Для каждого сегмента высчитать средний цвет – так мы и получим палитру.

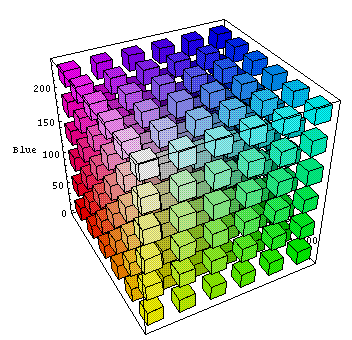
Что здесь можно улучшить? Первое, что приходит в голову – вычислять средний цвет не тупо сложив все цвета и разделив на их количество [ sum(color) / count(color) ], а с учётом, сколько раз каждый цвет встречается в изображении. То есть каждый цвет умножаем на количество его вхождений в изображении, полученные значения складываем, результат делим на количество вхождений в изображении всех цветов данного сегмента [ sum(color * total) / sum(total) ]. В результате, наиболее часто встречаемые цвета имеют приоритет при вычислении, но и редкие цвета вносят свои корректировки, поэтому палитра получается лучше, визуальное отклонение цветов меньше. Для лучших результатов желательно ещё учитывать гамму, но я оставил это на потом. Второе не так явно – медианное сечение совсем не учитывает особенности восприятия цвета человеческим глазом. Оттенки зелёного мы воспринимаем гораздо лучше оттенков синего. Я решил исправить это недоразумение и «сплющил» куб – длины сторон помножил на коэффициенты из этой статьи. В результате по зелёной и красной стороне сечений стало больше, по синей меньше. Такого решения я больше нигде не встречал (может плохо искал), но результат на лицо.
Теперь у нас есть оптимальная палитра, не идеальная конечно (я знаю, что её можно ещё улучшить), но достаточно хорошая. Следующий шаг – индексирование цветов изображения. Самый простой вариант – в каком сегменте находится цвет, такой и индекс. Быстро и просто. Но есть одно но, и даже не одно, поэтому к данному шагу мы ещё вернёмся.
Есть ещё один способ улучшить качество получаемого изображения – рассеивание ошибок. Тут тоже всё довольно просто – из индексируемого цвета вычитаем соответствующий цвет палитры, получаем ошибку, рассеиваем её по соседним пикселям в соответствии с определённой формулой (шаблоном), самая известная формула Флойда-Стейнберга, её я и использовал. При рассеивании ошибок размываются резкие переходы между цветами, и визуально кажется, что изображение содержит больше оттенков (цветов). Если интересно – про рассеивание ошибок подробно и интересно можно почитать тут. Этот алгоритм я так же решил допилить, помножив ошибку на всё те же коэффициенты, как оказалось, это была очень хорошая идея – так как сечений по синему диапазону стало меньше, в нём получалась значительная ошибка, и без корректировки ошибки коэффициентами рассеивание вносило много «шума».
Вот теперь можно снова вернуться к индексированию. Рассеиванием ошибок мы изменяем цвета пикселей и получаем такие, которых нет в нашем RGB-кубе (напомню, он составлен исключительно из цветов изображения). Теперь нельзя просто посмотреть в каком сегменте находится цвет, чтобы назначить индекс. Решение нашлось сразу – поиск ближайшего цвета в палитре. В данную формулу я подставил всё те же коэффициенты. Сравнивая результаты подбора цвета палитры по индексу сегмента в который входит исходный цвет и результаты поиска ближайшего цвета, наглядно увидел, что ближайший цвет часто оказывается в соседнем сегменте. Если исходный цвет находится ближе к центру сегмента – то индекс сегмента соответствует индексу цвета в палитре, но чем ближе исходный цвет к краям сегмента, тем больше вероятность, что ближайший цвет окажется в соседнем сегменте. В общем, единственный правильный путь индексирования – поиск ближайшего цвета в палитре. Но у поиска есть минус – он медленный, очень медленный. Писать числодробилку на python плохая идея.
Ну вот, хотел объяснить в двух словах, а получилась целая куча непонятной писанины. Надеюсь, код я пишу лучше, чем объясняю, поэтому вот ссылочка на github. Код несколько раз переписывался, сначала совершенствовался алгоритм, пока результат меня не устроил, потом оказалось, что он жрёт слишком много оперативы при обработке фотографий (сначала тестировал на небольших картинках), пришлось перенести RGB-куб, медианное сечение и карту пикселей в базу данных (sqlite). Скрипт работает очень медленно, но результат получается лучше, чем квантизация средствами PIL/Pillow и GIMP’ом (в нём эта операция называется индексирование).

Результат квантизации в GIMP, оптимальная палитра на 256 цветов + размывание цвета по Флойду-Стенбергу (нормальное)

Результат квантизации PIL/Pillow
image.convert(mode='P', dither=PIL.Image.FLOYDSTEINBERG, palette=PIL.Image.ADAPTIVE, colors=256)
Результат квантизации моим кодом

На что обратить внимание: рассеивание ошибки у GIMP сильно «шумит», PIL/Pillow создает не очень оптимальную палитру и практически не рассеивает ошибки (резкие переходы между цветами).
Если не видите разницу — посмотрите другие примеры на github.
P.S.: есть замечательная программа Color Quantizer, которая справляется с данной задачей лучше и быстрее, поэтому практического смысла мой скрипт не имеет, сделан исключительно из «спортивного» интереса.
Комментарии (28)
Oxoron
18.11.2016 11:17+1результат на лицо
Всегда нравились подобные двусмысленности в статьях. Всегда интересно, специально автор фразу подбирал, или случайно вышло.
P.S. Это не про орфографию.
Shrim
18.11.2016 11:40+3Изначально хотел повториться «палитра получается лучше, визуальное отклонение цветов меньше», но мне показалось, что повторов в статье итак много, исправил на первое, что пришло в голову.
Хотя, посмотрите на лицо Лены, разве не результат? Можете на github сравнить с тем, что с ней сделали GIMP и PIL.
А вообще, мне статья не нравиться целиком и полностью, не удалось мне правильно изложить свои мысли, но я не уверен, что смогу переписать её лучше.

WP_Hedgehog
18.11.2016 11:52Сколько искал, так и не смог найти программу, способную привести изображение к необходимому набору цветов, при условии, что палитра шире 256 значений (нужно было разложить на ~430 цветов).
Может кто подскажет что-нибудь подходящее?
x128
18.11.2016 20:59Color Quantizer позволяет задать произвольное количество цветов.

WP_Hedgehog
18.11.2016 21:06Большое спасибо!
Пробные прогоны вызвали массу положительных эмоций. Жаль, раньше не знал о такой полезной утилите.

herr_kaizer
18.11.2016 12:19Одно время хотел написать про это статью, но руки так и не дошли.
ИМХО, метод медианного среза нагляднее показывать не на RGB-кубе, а на массиве пикселей в изображении (R,G,B,A,R,G,B,A...). Сортируем массив по наибольшему range (не знаю, как по-русски сказать) цветового канала, делим массив пополам и проделываем то же самое в половинках, пока количество массивов не станет равно количеству необходимых цветов, усредняем значение цвета в каждом куске и возвращаем пиксели на место.
А метод на деревьях квадрантов даёт меньше искажений и имеет больше простора для оптимизации.
Shrim
18.11.2016 12:33Посмотрите код, именно так и реализовано. Просто представить RGB-куб проще, поэтому обычно его в пример и приводят.
Как я сказал в предыстории, это проект выходного дня. Теперь охота разобраться с octree и k-средних, так что, может статья будет иметь продолжение.
herr_kaizer
18.11.2016 12:38Не, я как раз не про сам алгоритм говорю, а его представление. Лично мне RGB куб не кажется наглядным.

encyclopedist
18.11.2016 12:33Честно говоря, мне результат Гимпа нравится больше всего. Особенно заметно на большом ярком соцветии в центре — у вашего алгоритма есть заметная постеризация.

encyclopedist
18.11.2016 12:40Посмотрел другие примеры. Ленну ваша программа обработала лучше. А вот на "пустыне" опять постеризация (появились горизонтальные полосы на небе около горизонта), в отличие от Гимпа.

Shrim
18.11.2016 12:55Вы не путаете? Полосы у PIL, у моего результата полосы почти не заметны. У GIMP явно видно рассеивание ошибки, изображение получается в крапинку. Что скажите про Маяк? На нём все эти недостатки видны очень хорошо.

encyclopedist
18.11.2016 13:02Точно не путаю. Да, у Гимпа шума намного больше. Но вопрос видимо в чуствительности разных людей к разным искажениям. Для меня шум гораздо меньше портит изображение чем полосы. Маяк у вас вышел лучше.

Shrim
18.11.2016 13:08Сейчас подумалось: по Флойду-Стейнбергу рассеивание только по соседним пикселям, поэтому постеризация всё ещё заметна (без рассеивания ошибки она явная). Наверное формулы «Jarvis, Judice, and Ninke », «Stucki » и «Sierra-3» дали бы лучший результат, за счёт большего поля рассеивания.

Shrim
18.11.2016 12:47Сохраните картинки и сравните их в полном размере. У GIMP результат очень шумный, при уменьшении это не так заметно (скорей всего на это и рассчитано).

PaulZi
18.11.2016 13:33Недавно решал такую задачу на JavaScript. Я правда применял кластеризацию K-Means (в задаче необходимо было найти небольше число основных оттенков), и преобразовывал в цветовое пространство Lab (это пространство специально создано для того, чтобы понимать на сколько отличаются цвета с точки зрения человеческого восприятия).
masai
18.11.2016 13:56Жалко, что статья очень короткая. При таком многообещающем названии можно было рассказать побольше. Хотя бы про ту же формулу Флойда — Стейнберга побольше или про кластеризацию, скажем, методом k средних.


VaalKIA
На жёлтом пухе появились блики, кромка крыла стала зелёной, палитрой это объяснить сложно, это явные искажения цветов, поскольку и синий и жёлтый в палитре остался.
Вообще говоря. расстояния между цветами в кубе — это не расстояния между цветами, а не пойми что, надо на это обратить внимание.
Shrim
Искажения цвета объясняются приоритетом зелёного канала при сечении. Там где блики — пух на оригинальном изображении самый светлый, GIMP и PIL это просто проигнорировали, затемнив данные участки. Край крыла на оригинале светло-голубой, из-за приоритета зелёного канала оттенков синего в палитре меньше, поэтому ближайшим к светло-голубому оказался свело-зелёный, GIMP и PIL сделали этот участок серым.
При усечении 300 000 цветов до 256 искажения в любом случае будут, главное — постараться сделать их наименее заметными.
По поводу расстояния между цветами в кубе — именно поэтому я и использовал коэффициенты, чтобы при вычислении расстояния учитывать относительную яркость цвета. Медианное сечение позволяет разделить куб на сегменты содержащие равное количество цветов, я при сечении учёл относительную яркость. Так же относительная яркость учитывается при поиске ближайшего цвета и рассеивании ошибок. А вот вычисление «среднего» цвета сегмента реализовано не лучшим образом. По хорошему надо ещё учитывать гамму.
Deosis
Скажите, а вы пробовали разбивать не куб RGB, а HSL?
3aicheg
Или CMYK-гиперкуб.
Shrim
Не пробовал, но в планах было, а так же разобраться с гаммой. Пока занят другим проектом.